Συλλογή ασκήσεων στην Άλγεβρα

wfgl · 26-08-11

Λάθος.Όχι μόνο γι' αυτό αλλά και γιατί διαιρείς με το abcd που μπορεί να είναι αρνητικός

Guest 018946 · 27 Αυγούστου 2011

σωστα...

βαλε την σωστη αν μπορεις

Polkiu · 26-08-11

παιδιά, κάπου εκεί που βγάζετε την ρίζα δεν πρέπει να μπει και ένα απόλυτο??? λέω εγω...

wfgl · 26-08-11

Αρχική Δημοσίευση από dr.tasos:
Απο ΑΜ-ΓΜ εχω $\frac{a^{4}+b^{4}+c^{4}+d^{4}}4 \geq \sqrt[4]{a^{4}b^{4}c^{4}d^{4}}$ Πολζω με 4 και περνω την σχεση που ζητηται $a^{4}+b^{4}+c^{4}+d^{4} \geq 4abcd$ Διορθωστε με αν ειμαι λαθος.

Πως μου διέφυγε ??? :mad:

H AM-GM ισχύει για $a1,a2,a3...an > 0$ :sorry:

Guest 018946 · 26-08-11

οποτε λαθος η λυση?

wfgl · 24 Ιουνίου 2012

Αρχική Δημοσίευση από Polkiuzxc:
Επειδή είμαι στο χωριό και δεν έχω τα μέσα για να την λύσω, όταν την είχα λύσει την πρώτη αρχίζεις ότι 11<12 και πας συνθετικά και βγάζεις αυτό που εΙπες. Οταν πάω Αθήνα θα σας ανεβάσω την λύση.

Μπορείς να ανεβάσεις τη λύση ???

Αρχική Δημοσίευση από wfgl:
Για την πρώτη άσκηση έχουμε

${a}^{2}+{b}^{2}+2=2(a-b) <=> {(a-1)}^{2}+{(b+1)}^{2}=0 <=> (a,b)=(1,-1)$

Με αντικατάσταση στο πρώτο ερώτημα προκύπτει $0x<=7$ Άρα x E R
To δεύτερο ερώτημα με αντικατάσταση αποκτά την μορφή $0x>1$ που δεν επαληθεύεται για καμιά τιμή του x
Όσον αφορά την δεύτερη ισχύει ότι ${({a}^{r}+{b}^{r})}^{1/r}>{({a}^{r+1}+{b}^{r+1})}^{1/r+1}$ για $a,b,r$ θετικούς ακεραίους.
Απόδειξη : (Θα χρησιμοποιήσω την μαθηματική επαγωγή ή μέθοδο της τέλειας επαγωγής)
Για να αποδείξουμε έναν μαθηματικό ισχυρισμό $P(v)$ , ο οποίος είναι συνήθως ισότητα ή ανισότητα ακολουθούμε τα εξής βήματα:
α) Αποδεικνύουμε ότι η πρόταση $P(v)$ αληθεύει για τον μικρότερο φυσικό αριθμό που ορίζεται
β)Υποθέτουμε ότι η πρόταση αληθεύει για το φυσικό κ=ν
γ)τέλος αποδεικνύουμε ότι η πρόταση ισχύει για ν=κ+1
για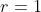 $r=1$ ${({a}^{1}+{b}^{1})}^{1}>{({a}^{2}+{b}^{2})}^{1/1+1}<=> 2ab >0$ που ισχύει αφού χ Ε Z+
Έστω ότι η πρόταση ισχύει για $r=k$
Για $r=k+1$ η πρόταση μετασxηματίζεται ως εξής :
${({a}^{k+1}+{b}^{k+1})}^{1/k+1}>{({a}^{(k+1)+1}+{b}^{(k+1)+1})}^{1/(k+1)+1}$
Θέτω $p=k+1 E Z+$ , αφού $k E Z+$ και γίνεται : ${({a}^{p}+{b}^{p})}^{1/p}>{({a}^{p+1}+{b}^{p+1})}^{1/(p+1}$ που ισχύει λόγω της υπόθεσης
Άρα λόγω αυτής της ανισότητας έχουμε : $\sqrt[11]{{11}^{11}+{12}^{11}}>\sqrt[12]{{11}^{12}+{12}^{12}}$

Αρχική Δημοσίευση από wfgl:
Αν $a,b,c,d$ τυχαίοι πραγματικοί αριθμοί
Νδο : ${a}^{4}+{b}^{4}+{c}^{4}+{d}^{4}>=4abcd$

Τελικά λύνεται έτσι : ${a}^{4}+{b}^{4}>=2{a}^{2}{b}^{2} (1)$
και
${c}^{4}+{d}^{4}>=2{c}^{2}{d}^{2} (2)$
$(1)+(2)<=>{a}^{4}+{b}^{4}+{c}^{4}+{d}^{4}>= 2({(ab)}^{2}+{(cd)}^{2})>=2*2abcd=4abcd$

Guest 018946 · 26-08-11

Αρχική Δημοσίευση από wfgl:
Τελικά λύνεται έτσι : ${a}^{4}+{b}^{4}>=2{a}^{2}{b}^{2} (1)$
και
${c}^{4}+{d}^{4}>=2{c}^{2}{d}^{2} (2)$
$(1)+(2)<=>{a}^{4}+{b}^{4}+{c}^{4}+{d}^{4}>= 2({(ab)}^{2}+{(cd)}^{2})>=2*2abcd=4abcd$

απο που τις βρισκεις? αυτες τις ασκησεις?

wfgl · 26-08-11

Από e-books και από βιβλία μαθηματικών διαγωνισμών

Guest 018946 · 26-08-11

Αρχική Δημοσίευση από wfgl:
Από e-books και από βιβλία μαθηματικών διαγωνισμών

απο ποια e-books αμα εχεις και ελληνικα e-books στειλε μου κανα λινκ σε πμ. Βαλε και καμια αλλη ασκηση να παιδευτουμε λιγο...

ξαροπ · 26 Αυγούστου 2011

Κι ένας τρίτος τρόπος, έτσι, για να υπάρχει....(χρησιμοποιεί άγνωστη θεωρία)

i) Αν ένας ή τρεις εκ των a,b,c,d αρνητικοί, η ανισότητα είναι προφανής (μη αρνητικό μεγαλύτερο ή ίσο από μη θετικό)

i) Αν δύο ή τέσσερις εκ των a,b,c,d αρνητικοί, τότε στη θέση κάθε αρνητικού, πχ. του a, θέτουμε a = - k και παρατηρούμε ότι η ανισότητα δεν αλλάζει αφού $(-k)^4 = a^4$ και στο δεξί μέρος έχουμε πολλαπλασιασμό άρτιου πλήθους αρνητικών (δηλαδή καταλήγουμε πάλι στο αρχικό δεξί μέρος της ανισότητας με μη αρνητικούς όρους αυτή τη φορά)

iii) Αν τουλάχιστον ένας από τους a,b,c,d ισούται με μηδέν, τότε έχουμε να δείξουμε ότι $a^4 + b^4 + c^4 + d^4 \geq 0$ , που προφανώς ισχύει (με ισότητα για a=b=c=d=0)

iv) Έστω $a,b,c,d >0$

Επειδή $(4,0,0,0) > (1,1,1,1)$ ,

η ανισότητα Muirhead μας δίνει $\sum a^4b^0c^0d^0 \geq \sum a^1b^1c^1d^1$

$\Leftrightarrow 6(a^4+b^4+c^4+d^4) \geq 4!abcd \Leftrightarrow a^4+b^4+c^4+d^4 \geq 4abcd$ ,

με ισότητα για a=b=c=d

Άλλη άσκηση:

Αν $n, k, l$ φυσικοί με $n = k+l$ , να ελέγξετε αν ισχύει

$a^n + b^n \geq a^kb^l + a^lb^k$ για όλους τους θετικούς α,β.

papas · 26-08-11

Αρχική Δημοσίευση από wfgl:
Τελικά λύνεται έτσι : ${a}^{4}+{b}^{4}>=2{a}^{2}{b}^{2} (1)$
και
${c}^{4}+{d}^{4}>=2{c}^{2}{d}^{2} (2)$
$(1)+(2)<=>{a}^{4}+{b}^{4}+{c}^{4}+{d}^{4}>= 2({(ab)}^{2}+{(cd)}^{2})>=2*2abcd=4abcd$

Note : χρησιμοποιησε την ανισοτητα χ^2+y^2 >= 2xy ,που ισχυει για καθε x,y που ανηκει στο R

Ασκηση απο αλγεβρικες ανισοτητες του Στεργιου ειναι.Την κοιταγα σημερα :p

wfgl · 27 Αυγούστου 2011

Χμμ ...
Θα χρησιμοποιήσω την πολυαγαπημένη μου ανισότητα, την ανισότητα της αναδιάταξης :
Έστω, λόγω της ομοιογένειας ότι $a>=b$
${a}^{k}{a}^{l}+{b}^{k}{b}^{l}>={a}^{k}{b}^{l}+{a}^{l}{b}^{k}$
Έστω ${n}_{1}=({a}^{k},{b}^{k})$ και ${n}_{2}=({a}^{l},{b}^{l})$
Εφαρμόζοντας την ανισότητα της αναδιάταξης έπεται : ${a}^{k}{a}^{l}+{b}^{k}{b}^{l}>={a}^{k}{b}^{l}+{a}^{l}{b}^{k}<=>{a}^{n}+{b}^{n}>={a}^{k}{b}^{l}+{a}^{l}{b}^{k}$
Θα μπορούσες να μας εξησήσεις την ανισότητα Muirhead ???

Βάλτε καμιά ασκησούλα να λύσουμε

ξαροπ · 26-08-11

Ωραία, η άσκηση λύνεται και με τελείως στοιχειώδη μέσα (μην ξεχνάτε την πιο απλή σκέψη στις ανισότητες, αν $a>b$ τότε $a-b > 0$ !)

Λίγα λόγια για τη Muirhead, από ένα ενδιαφέρον άρθρο πάνω σε ανισότητες σαν κι αυτή, στο spoiler.

Αν για δυο ακολουθίες πραγματικών αριθμών $a_1, a_2, ..., a_n, b_1, b_2,...b_n$ ισχύει:

1. $a_1 \geq a_2 \geq...\geq a_n$ και $b_1 \geq b_2 \geq...\geq b_n$

2. Για κάθε $i \in (1,2,...,n-1)$ ισχύει $\sum_{k=1}^{i}a_k \geq \sum_{k=1}^{i}b_k$

3. $\sum_{i=1}^{n}a_i = \sum_{i=1}^{n}b_i$

Τότε λέμε ότι $(a_1, a_2, a_3,...a_n) > (b_1, b_2, b_3,...b_n)$ ,

δηλαδή ότι η ακολουθία (α) μεγιστοποιεί την ακολουθία (β)

Πχ. (4,0,0,0) > (1,1,1,1) διότι

1. 4 > 0=0=0, 1=1=1=1,

2. 4+0 = 4+0+0 > 1+1+1 > 1+1 > 1,

3. 4 = 1+1+1+1

Για n=2 και για θετικούς x,y παίρνουμε

$x^{a_1}y^{a_2} + x^{a_2}y^{a_1} \geq x^{b_1}y^{b_2} + x^{b_2}y^{b_1}$

Όμοια και για περισσότερους από δύο όρους, αρκεί να προσέχουμε ότι το άθροισμα είναι απόλυτα συμμετρικό (και όχι κυκλικά), πχ. για τρεις όρους (τρεις εκθέτες δηλαδή) θα είχαμε όλες τις δυνατές μετατοπίσεις εκθετών, δηλαδή $3! = 6$ όρους σε κάθε μέρος της ανισότητας.

(όμοια και $4! = 24$ για τέσσερις όρους)

Η άσκηση που έδωσα "λιώνεται" επίσης σε μία γραμμή από τη Muirhead, επίσης η γενικευμένη ΑΜ-ΓΜ αποδεικνύεται από τη Muirhead, αν θέλετε να ξέρετε έναν τρόπο εκτός από επαγωγή.

Και μια άλλη (γνωστή) άσκηση:

Για ποιούς ακεραίους $x,y$ οι παρακάτω παραστάσεις είναι πρώτοι αριθμοί;

1. $A = x^4 +4y^4$

(*) 2. $B = x^8 + 2^{2^x+2}$ (Αρχιμήδης 2008, 2ο πρόβλημα στους μεγάλους)

Guest 018946 · 30 Αυγούστου 2011

μπορει καποιος να παρουσιασει την ανισοτητα της αναδιαταξης με 1-2 λυμενα παραδειγματα για να μπορουμε να την εφαρμοσουμε και οι υπολοιποι?

επανερχομαι και παλι με ανισοτητες: 1) Για $a,b,c \geq 0$ να δειξετε οτι $\frac{2}{x+y}+\frac{2}{y+z}+\frac{2}{x+z} \geq \frac{9}{x+y+z}$

και αλλη μια 2) Για $a,b,c,x,y,z \geq 0$ να δειξετε οτι $\frac{x}{ay+bz}+\frac{y}{az+bx}+\frac{z}{ax+by} \geq \frac{3}{a+b}$

rebel · 30-08-11

Αρχική Δημοσίευση από dr.tasos:
επανερχομαι και παλι με ανισοτητες: 1) Για $a,b,c \geq 0$ να δειξετε οτι $\frac{2}{x+y}+\frac{2}{y+z}+\frac{2}{x+z} \geq \frac{9}{x+y+z}$

$\left( \frac{2}{x+y}+\frac{2}{y+z}+\frac{2}{x+z} \right) (x+y+z)=\left( \frac{1}{x+y}+\frac{1}{y+z}+\frac{1}{x+z} \right)(2x+2y+2z)=\left( \frac{1}{x+y}+\frac{1}{y+z}+\frac{1}{x+z} \right)\left[(x+y)+(y+z)+(x+z)\right]\stackrel{Cauchy-Schwarz}{\geq}\left( \sqrt{\frac{x+y}{x+y}} + \sqrt{\frac{y+z}{y+z}} + \sqrt{\frac{x+z}{x+z}} \right)^2=9$

Για την Cauchy-Schwarz δείτε εδώ

Guest 018946 · 30-08-11

μπορει και αλλιως με αντρεσκου και μετα στο τελος βγαινει το ζητουμενο με μεταβατικη.Βασικα αντικαθιστας το 2 με ${\sqrt[2]{2}}^2$ και εφαρμοζεις ανετα αντρεσκου.

wfgl · 30-08-11

Γενικά δεν θα έπρεπε $x,y,z>0$ αντί για $x,y,z>=0$
Θα ήθελα να ρωτήσω, τι περιέχει το βιβλίο Κλασικές Και Νέες Ανισότητες του Μπάμπη Στεργίου ??? (γιατί έχω ήδη τις Αλγεβρικές Ανισότητες και αναρωτιέμαι αν θα το αγοράσω...)

Guest 018946 · 31-08-11

μολις ειδα ακομη μια που με αρεσε : Για $a,b,c > 0$ Νδο : $\frac{a^{2}+b^{2}}{a+b}+\frac{b^{2}+c^{2}}{b+c}+\frac{a^{2}+c^{2}}{a+c} \geq a+b+c$

wfgl · 31-08-11

Αρχική Δημοσίευση από dr.tasos:
μπορει και αλλιως με αντρεσκου και μετα στο τελος βγαινει το ζητουμενο με μεταβατικη.Βασικα αντικαθιστας το 2 με ${\sqrt[2]{2}}^2$ και εφαρμοζεις ανετα αντρεσκου.

Αρκεί $x,y,z>0$ Εσύ μας δίνεις $a,b,c>=0$

Αρχική Δημοσίευση από dr.tasos:
μολις ειδα ακομη μια που με αρεσε : Για $a,b,c > 0$ Νδο : $\frac{a^{2}+b^{2}}{a+b}+\frac{b^{2}+c^{2}}{b+c}+\frac{a^{2}+c^{2}}{a+c} \geq a+b+c$

Σπας τα κλάσματα και εφαρμόζεις Andreescu.

Guest 018946 · 31-08-11

Αρχική Δημοσίευση από wfgl:
Αρκεί $x,y,z>0$ Εσύ μας δίνεις $a,b,c>=0$

Σπας τα κλάσματα και εφαρμόζεις Andreescu.

σωστος στην λυση σου. Μεχρι πριν λιγο δεν ηξερα να βαζω το $>$ αλλα μονο το $\geq$

Συλλογή ασκήσεων στην Άλγεβρα

Νεοφερμένος

Guest 018946

Επισκέπτης

Πολύ δραστήριο μέλος

Νεοφερμένος

Guest 018946

Επισκέπτης

Νεοφερμένος

Guest 018946

Επισκέπτης

Νεοφερμένος

Guest 018946

Επισκέπτης

Πολύ δραστήριο μέλος

Διάσημο μέλος

Νεοφερμένος

Πολύ δραστήριο μέλος

Guest 018946

Επισκέπτης

Πολύ δραστήριο μέλος

Guest 018946

Επισκέπτης

Νεοφερμένος

Guest 018946

Επισκέπτης

Νεοφερμένος

Guest 018946

Επισκέπτης