Ryuzaki
Πολύ δραστήριο μέλος


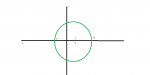
Εμενα μου βγηκε κυκλος με κεντρο το Κ(0,0) και ακτινα ρ=(ριζα 2) / 2
ΕΞΑΙΡΕΙΤΑΙ ΤΟ ΣΗΜΕΙΟ Κ(0,0) αφου δεν πρεπει χ=0 ΚΑΙ y=0 (ταυτοχρονα και τα δυο μηδεν)
Σωστός, είναι ο άξονας y'y(χ=0) και ο κύκλος με κέντρο Κ(0,0) (εξαιρείται K(0,0)) και ρ=1/2 όμως...
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


2) Βρηκα χ^2 +Y^2 =1/2 αρα η ακτινα ειναι ρ=(ριζα2)/2 .Κανω λαθος;
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Ryuzaki
Πολύ δραστήριο μέλος


Έστω1) πως ακριβως βρηκες τον y'y;
2) Βρηκα χ^2 +Y^2 =1/2 αρα η ακτινα ειναι ρ=(ριζα2)/2 .Κανω λαθος;




Άρα

Άρα
Οπότε










Οπότε, ο ΓΤ του z είναι ο άξονας y'y (αφού χ=0) και ο κύκλος με κέντρο Κ(0,0) (εξαιρείται K(0,0) αφού x,yεR και είναι διαφορετικά από 0) και

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


Γι αυτο πρεπει να ελεγχω την ασκηση μετα την ολκληρωση της
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


χρησιμοποιήθηκε ο τύπος για το πεπερασμένο άθροισμαόρων γεωμετρικής προόδου με πρώτο όρο 1 και λόγο -i. Τώρα
και αντικατέστησες. Τώρα που έβγαλες κοινό παράγοντα το i^3 δεν είναι πρώτος όρος το 1;
Θα μπορούσα και να μην το είχα βγάλει. Απλά αυτό που μένει μέσα στην παθένθεση είναι άθροισμα όρων γεωμετρικής προόδου με πρώτο όρο το 1 οπότε μου αρέσει περισσότερο έτσι. Λυπάμαι αν σε μπέρδεψα.
ναι
 Εχω κάποιες ακόμα απορίες
Εχω κάποιες ακόμα απορίες1) εννοώ οτι το α1 δεν θα έπρεπε να ήταν το 1; αφου πρώτος όρος είναι το 1 εφόσον έβγαλες κοινό παράγοντα το i^3.
2)Βοήθημα Μπάρλας, σελίδα 37, Διαγώνισμα, Θέμα 2:
Έστω
α. Να βρείτε τους
βγαίνουν δύο συστήματα ένα με το y=0 και ένα με το x=-1 και αυτές είναι και οι λύσεις μου. Όμως στο βοήθημα την λύση την έχει: (x=-1 και y=0) ή (x=1 και y=+-
3)Βοήθημα Μπάρλας, σελίδα 57, άσκηση 2ιχ: Αν οι εικόνες των μιγαδικών z1,z2,z3 δεν είναι συνευθειακά σημεία, τότε το σύστημα
4)Άσκηση: Δίνεται το τριώνυμο
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


4) καταρχην στο τρυονυμο βαζεις F ενω στο ζητουμενο f .
Για να ισχυει η σχεση που θελεις πρεπει α>0 και Δ<=0 (οπου α ο συντελεστης του χ^2 και Δ η διακρινουσα του τριωνυμου)
α=1 αρα αρκει ν.δ.ο Δ<=0
Βρισκοντας σωστα την διακρινουσα κατεληξα στο Δ= -4(z1*(συζηγης)z2 + 1)*(1+z2*(συζηγης)z1)
Σου δινει κατι αλλο απο προηγουμενα ερωτηματα ; Το οτιδηποτε ή ειναι ετσι η ασκηση;
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Ryuzaki
Πολύ δραστήριο μέλος


α)Ερώτημα του Μπαρλα (εμένα την άσκηση την έχει στη σελίδα 33)
Έκανα και εγώ τις πράξεις και βρήκα και εγώ χ=-1 και y=0. Κοίταξα και τον Μπάρλα που έχω (έκδοση 2004) και αυτές τις ρίζες έχει και όχι κάποια άλλη.. Παίζει να το είχε όπως λες παλιότερα και στη συνέχεια να το διόρθωσε.
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Σου απάντησα και πριν ότι πρώτος όρος είναι το 1. Αν το γράψω εντελώς τυπικά είναι1) εννοώ οτι το α1 δεν θα έπρεπε να ήταν το 1; αφου πρώτος όρος είναι το 1 εφόσον έβγαλες κοινό παράγοντα το i^3.
To
Κι εγώ τα ίδια βρίσκω. Πρέπει να έχουν λάθος οι λύσεις2)Βοήθημα Μπάρλας, σελίδα 37, Διαγώνισμα, Θέμα 2:
Έστω z ένας μιγαδικός που ικανοποιεί το σύστημα αυτό. Αφού οι εικόνες των μιγαδικών3)Βοήθημα Μπάρλας, σελίδα 57, άσκηση 2ιχ: Αν οι εικόνες των μιγαδικών z1,z2,z3 δεν είναι συνευθειακά σημεία, τότε το σύστημαέχει μοναδική λύση.
Συνεχίζω από κει που έφτασε ο Γιώργος. Θέτουμε4)Άσκηση: Δίνεται το τριώνυμο, όπου z1 και z2 είναι δύο μιγαδικοί αριθμοί. Να αποδείξετε οτι
για κάθε xεR. πως λύνεται αυτή;
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.



Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
kosmas13green
Νεοφερμένος


α) Re(α*(συζυγή του)β)=Re(β*(συζυγή του)γ)=Re(γ*(συζυγή του)α)=-1/2
β)|α-β|=ριζα3 πως λύνεται τούτη εδώ;

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Όμοια και για τα υπόλοιπα. Όσο για το δεύτερο ερώτημα:
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


Μαλλον ο Μπάρλας κάνει λάθος, δεν τις επαληθεύει τις εξισώσεις. Δεν ξες πόσο ενοχλητική/κουραστική είναι ο λατεξ, στο μηνυμά μου F=f. Γιατί α>0 και Δ<=0; Το α δεν είναι μόνο διαφορετικό του μηδενός;2) Και εγω τις ιδιες λυσεις βρηκα...Βαλε οπου χ=1 και y=+- (ριζα2)/2 και δες αν την επαληθευει. Αν οχι, τοτε ο Μπαρλας κανει λαθος
4) καταρχην στο τρυονυμο βαζεις F ενω στο ζητουμενο f .
Για να ισχυει η σχεση που θελεις πρεπει α>0 και Δ<=0 (οπου α ο συντελεστης του χ^2 και Δ η διακρινουσα του τριωνυμου)
α=1 αρα αρκει ν.δ.ο Δ<=0
Βρισκοντας σωστα την διακρινουσα κατεληξα στο Δ= -4(z1*(συζηγης)z2 + 1)*(1+z2*(συζηγης)z1)
Σου δινει κατι αλλο απο προηγουμενα ερωτηματα ; Το οτιδηποτε ή ειναι ετσι η ασκηση;
εγώ έχω του 2009. ποιος ξερει μαλλον καποιο λάθος.@gkm
α)Ερώτημα του Μπαρλα (εμένα την άσκηση την έχει στη σελίδα 33)
Έκανα και εγώ τις πράξεις και βρήκα και εγώ χ=-1 και y=0. Κοίταξα και τον Μπάρλα που έχω (έκδοση 2004) και αυτές τις ρίζες έχει και όχι κάποια άλλη.. Παίζει να το είχε όπως λες παλιότερα και στη συνέχεια να το διόρθωσε.
ααααααααααααααααααααααααααααααααα! ευχαριστώ πολύΣου απάντησα και πριν ότι πρώτος όρος είναι το 1. Αν το γράψω εντελώς τυπικά είναι
Toτο κουβαλάω μαζί αλλά δεν περιλαμβάνεται στον τύπο
του αθροίσματος.
Κι εγώ τα ίδια βρίσκω. Πρέπει να έχουν λάθος οι λύσεις
Έστω z ένας μιγαδικός που ικανοποιεί το σύστημα αυτό. Αφού οι εικόνες των μιγαδικώνδεν είναι συνευθειακά, σχηματίζουν τρίγωνο. H εικόνα του z ισαπέχει από τις κορυφές αυτού του τριγώνου και άρα συμπίπτει με το σημείο τομής των μεσοκαθέτων του τριγώνου, το οποίο είναι σημείο μοναδικό και ονομάζεται περίκεντρο του τριγώνου( Κέντρο του περιγεγραμμένου κύκλου του τριγώνου).
Συνεχίζω από κει που έφτασε ο Γιώργος. Θέτουμεοπότε η διακρίνουσα γράφεται
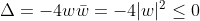





Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


είναι ύλη προηγούμενων ταξεων ε;Αυτες ειναι οι προυποθεσεις , ωστε ενα τριωνυμο να ειναι μεγαλυτερο ή ισο του μηδενος...
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


Μάλιστα...
 Ευχαριστώ όλους για τις απαντήσεις σας.
Ευχαριστώ όλους για τις απαντήσεις σας.
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
kosmas13green
Νεοφερμένος


Νομίζω ότι χρειαζόμαστε την επιπλέον υπόθεση ότι. Τότε έχουμε
Όμοια και για τα υπόλοιπα. Όσο για το δεύτερο ερώτημα:
=3 )


 Ευχαριστωωωω
Ευχαριστωωωω 
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
kosmas13green
Νεοφερμένος


α) Να βρείτε τη μέγιστη και την ελάχιστη τιμή του |z|
β)Αν ακόμη είναι |z+1/3|=12, τότε να βρείτε:
ι)το |w|
ιι) τον γεωμετρικό τόπο των εικόνων των μιγαδικών αριθμών u
Μια βοήθεια;
 Στο α) γενικώς δεν τα πάω καλά με τη μέγιστη και ελάχιστη τιμή, και στο β) ι) έχω κάνει 3wz+w=6*(συζυγή του)z-6 <=> wz+w/3=2*(συζυγή του)z-2 <=> w(z+1/3)=2((συζυγή του)z-1). To ii) δεν το άγγιξα
Στο α) γενικώς δεν τα πάω καλά με τη μέγιστη και ελάχιστη τιμή, και στο β) ι) έχω κάνει 3wz+w=6*(συζυγή του)z-6 <=> wz+w/3=2*(συζυγή του)z-2 <=> w(z+1/3)=2((συζυγή του)z-1). To ii) δεν το άγγιξα  Ευχαριστώ
Ευχαριστώ
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Guest 278211
Επισκέπτης


Δίνονται οι μιγαδικοί αριθμοί z,w,u για τους οποίους ισχύουν οι σχέσεις: |z-1|=6, 3wz+w=6*(συζυγή του)z-6 και (2u-1/2)((συζυγή του)u-1/4=8w*(συζυγή του)w.
α) Να βρείτε τη μέγιστη και την ελάχιστη τιμή του |z|
β)Αν ακόμη είναι |z+1/3|=12, τότε να βρείτε:
ι)το |w|
ιι) τον γεωμετρικό τόπο των εικόνων των μιγαδικών αριθμών u
Μια βοήθεια;Στο α) γενικώς δεν τα πάω καλά με τη μέγιστη και ελάχιστη τιμή, και στο β) ι) έχω κάνει 3wz+w=6*(συζυγή του)z-6 <=> wz+w/3=2*(συζυγή του)z-2 <=> w(z+1/3)=2((συζυγή του)z-1). To ii) δεν το άγγιξα
Ευχαριστώ

α) Το z ανήκει σε κύκλο με ακτίνα ρ=6 και κέντρο Α(1,0).
(ΟΑ)=1 και |z(max)|=(OA)+ρ=7 και |z(min)|=(OA)-ρ=5
Το σχήμα βοηθάει σε αυτές τις περιπτώσεις. Αυτό που σου ζητάει στην πραγματικότητα είναι να βρεις τα σημεία του κύκλου που απέχουν λιγότερο και περισσότερο από το Ο (0,0).
β) (i) Πρέπει να λύσεις το σύστημα: |z-1|=6 και |z+1/3|=12 θέτοντας z=x=yi με x,yER. Από εδώ θα βρεις είτε 1 είτε 2 τιμές για το z και με αντικατάσταση θα φτάσεις στο αποτέλεσμα.
(ii) (2u-1/2)((συζυγή του)u-1/4)=8w*(συζυγή του)w <=> 2*(u-1/4)((συζυγή του)u-1/4)=8w*(συζυγή του)w <=> |u-1/4|²=4|w|² <=>
|u-1/4|=2|w| κτλ
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


min|z|= ρ-1=6-1=5
max|z|=ρ+1=6+1=7
β) Λυσε την δευτερη σχεση ως προς w και θα βγει w=6(z-1)/3z+1= 2(z-1)/(z+1/3) [δεν υπαρχει προβλημα με τον παρανομαστη αφου z διαφορο του -1/3 (σου λεει οτι |z+1/3|=12) ]
αρα |w|= 2|(z-1)/(z+1/3)|=...=2*6/12=1 , οποτε |w|=1
Το τριτο θα το δω αργοτερα

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Συνημμένα
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 41 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 226 μέλη διάβασαν αυτό το θέμα:
- trifasikodiavasma
- haji
- thepigod762
- Mariosm.
- soulatso
- oteletampis
- phleidhs
- Hased Babis
- AggelikiGr
- sir ImPeCaBlE
- veiNqh
- Scandal
- alekos
- Debugging_Demon
- just some guy
- xristosgkm
- ismember
- Apocalypse
- arrow25
- rempelos42
- ggl
- GStef
- QWERTY23
- xrisamikol
- Σωτηρία
- nikoletaz57
- _Aggelos123
- Mariam38
- SlimShady
- strsismos88
- Georgekk
- Lia 2006
- igeorgeoikonomo
- marian
- tsiobieman
- constansn
- Xristosdimitra
- Panagiotis849
- ρενακι 13
- Memetchi
- eukleidhs1821
- Nikkkpat
- Unboxholics
- korlef
- kwstaseL
- Thanos_D
- the purge
- T C
- Giii
- Papachrist
- liaiscool
- Αννα Τσιτα
- globglogabgalab
- Pharmacist01
- thanahss
- abcdefg12345
- nicole1982
- thecrazycretan
- kvstas92
- KingOfPop
- maria301
- papa2g
- stefan
- Κλημεντίνη
- TonyMontanaEse
- Athens2002
- Alexecon1991
- Μάρκος Βασίλης
- Cortes
- το κοριτσι του μαη
- calliope
- ale
- panagiotis G
- Kleanth
- aggelosst9
- BioChemical
- spring day
- nucomer
- Georgia110
- LeoDel
- pink_panther
- Alexandros973
- marsenis
- den antexw allh apotyxia
- KaterinaL
- kiyoshi
- drosos
- Λαμπρινηη
- Bill22
- Chrysablac.
- giorgosp97
- Βλα
- Monster Hunter
- jul25
- xxxtolis
- Stroka
- nicks1999
- totiloz
- Earendil
- mitsakos
- tasost
- lnesb
- ssalex
- Vasilina93
- alan09
- Livaja10
- χημεια4λαιφ
- Viedo
- UncleJ
- Kostakis45
- Infrared
- Zgian
- pepatogourounaki
- hirasawayui
- GeoCommand
- Eleni54
- American Economist
- EiriniS20
- ΘανάσοςG4
- stamoul1s
- Αριάνα123
- uni77
- Libertus
- tasoss
- PanosCh002
- Unseen skygge
- Νικόλας Ραπ.
- cel123
- The Limit Does Not Exist
- don_vito
- suaimhneas
- Αλκης Κ.
- alexrami
- Baggelitsa36
- Νομικάριος13
- spinalgr1990
- d_th
- Adolfo valencia
- Πα.Κ
- Vasilis25
- Johnman97
- Steffie88
- rekcoR
- gwgw_5
- fockos
- Mariahj
- roud
- kostas83
- Cpt.Philips
- Makis45
- Χρησλου
- Panos_02
- Vold
- tymvorixos
- GiorgosAsi
- Neos167
- theodoraooo
- George187
- Άρτεμις Α.
- Μαρία2222
- christos87
- Idontknoww
- jimis2001
- Metamorph
- Γατόπαρδος.
- Johnsk
- mitsos14
- johnsiak
- Elel
- Dreamer_SW
- Γιαννης1987Θεσσ
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki