μπαμπης5304
Νεοφερμένο μέλος





 (Ευχαριστω Anyway!!!!!)
(Ευχαριστω Anyway!!!!!)Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
kesmarag
Νεοφερμένο μέλος


Διάρκεια 3 ώρες
Ύλη : Ορισμός Συνάρτησης, Σύνθεση, Μονοτονία
Σύντομα θα αναρτήσω και τις λύσεις
https://www.math24.gr/pdf/lck/Diagonisma_B1.1_1.3.pdf
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
μπαμπης5304
Νεοφερμένο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
antwwwnis
Διάσημο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
vassilis498
Διακεκριμένο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
μπαμπης5304
Νεοφερμένο μέλος



Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
lowbaper92
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Αρχικά λύνω την εξίσωση
Έυκολα αποδεικνύεται με βάση την πρώτη δοθείσα σχέση οτι η
Από
επομένως
Έστω τώρα
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Leo 93
Εκκολαπτόμενο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


 . Αν έχεις χρόνο γράψε και την λύση σου.
. Αν έχεις χρόνο γράψε και την λύση σου.Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος


Αν για τους μιγαδικούςισχύει
καί
να βρεθεί το
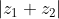
Μια κάπως ανορθόδοξη λύση που μας δίνει περισσότερα στοιχεία από όσα θέλουμε.
Αν z=x+yi όπου x, y ανήκουν R και ισχύει |z-i|=1 τότε έχουμε διαδοχικά |x+(y-1)i|=1 => |x+(y-1)i|^2=1 => (x^2)+(y-1)^2=1
Η παραπάνω εξίσωση παριστάνει κύκλο με κέντρο K(0,1) και ακτίνα ρ=1. Οι παραμετρικές εξισώσεις αυτού του κύκλου είναι x=συνθ, y=1+ημθ όπου 0<=θ<2π
Άρα z1=συνθ1+(1+ημθ1)i, z2=συνθ2+(1+ημθ2)i όπου 0<=θ1<2π και 0<=θ2<2π.
Έχουμε z1-z2=(συνθ1-συνθ2)+(ημθ1-ημθ2)i
Συνεπώς |z1-z2|^2=(συνθ1-συνθ2)^2+(ημθ1-ημθ2)^2=(συνθ1)^2+(συνθ2)^2-2συνθ1συνθ2+(ημθ1)^2+(ημθ2)^2-2ημθ1ημθ2=
=[(ημθ1)^2+(συνθ1)^2]+[(ημθ2)^2+(συνθ2)^2]-2(συνθ1συνθ2+ημθ1ημθ2)=(1+1)-2συν(θ1-θ2)=2-2συν[-(θ2-θ1)]=2[1-συν(θ2-θ1)]>=0 αφού συν(θ2-θ1)<=1
|z1-z2|=2 => |z1-z2|^2=4 => 2(1-συν(θ2-θ1))=4 => 1-συν(θ2-θ1)=2 => συν(θ2-θ1)=-1 => συν(θ2-θ1)=συνπ => θ2-θ1=(2κ+1)π => θ2=θ1+(2κ+1)π, κ ανήκει Ζ
0<=θ1<2π => -2π<-θ1<=0
0<=θ2<2π
Άρα -2π<θ2-θ1<2π => -2π<2κπ+π<2π => -3π<2κπ<π => -(3/2)<κ<(1/2) => κ=-1 ή κ=0
Για κ=-1 είναι θ2=θ1-π
0<=θ2<2π => 0<=θ1-π<2π => π<=θ1
 π και επειδή 0<=θ1<2π τότε πρέπει π<=θ1<2π
π και επειδή 0<=θ1<2π τότε πρέπει π<=θ1<2πΑν θ1=θ τότε θ2=θ-π και ημθ2=ημ(θ-π)=-ημ(π-θ)=-ημθ, συνθ2=συν(θ-π)=συν(π-θ)=-συνθ
Για κ=0 είναι θ2=θ1+π
0<=θ2<2π => 0<=θ1+π<2π => -π<=θ1<π και επειδή 0<=θ1<2π τότε πρέπει 0<=θ1<π
Αν θ1=θ τότε θ2=θ+π και ημθ2=ημ(θ+π)=ημ(π-(-θ))=ημ(-θ)=-ημθ, συνθ2=συν(θ+π)=συν(π-(-θ))=-συν(-θ)=-συνθ
Και στις 2 περιπτώσεις είναι ημθ2=-ημθ, συνθ2=-συνθ
Συνεπώς z1=συνθ1+(1+ημθ1)i=συνθ+(1+ημθ)i, z2=συνθ2+(1+ημθ2)i=-συνθ+(1-ημθ)i όπου 0<=θ<2π
Έχουμε z1+z2=2i. Άρα |z1+z2|=|2i|=|2||i|=2*1=2
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


 . Μαλλον πρωτότυπη παρά ανορθόδοξη εγώ θα έλεγα. Περιμένω όμως και σχολικές λύσεις.
. Μαλλον πρωτότυπη παρά ανορθόδοξη εγώ θα έλεγα. Περιμένω όμως και σχολικές λύσεις.Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
soras7
Νεοφερμένο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


Η σχέση |z1-i|=|z2-i|=1 μας λέει ότι z1 και z2 βρίσκονται πάνω στον ίδιο καθορισμένο κύκλο με κέντρο το z=i και ακτίνα 1.
Η σχέση |z1-z2|=2 μας λέει ότι τα z1 και z2 είναι αντιδιαμετρικά.
Άρα μπορούμε να γράψουμε:
z1=z+z0 και z2=z-z0.
Άρα |z1+z2|=|2z|=|2i|=2.
ο.ε.δ.
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
soras7
Νεοφερμένο μέλος


Oντως πρεπει να σκεφτομαστε πιο απλαΝα σκέφτεστε απλά. Να χρησιμοποιείτε όσο πιο άμεσα γίνεται τα δεδομένα.
Η σχέση |z1-i|=|z2-i|=1 μας λέει ότι z1 και z2 βρίσκονται πάνω στον ίδιο καθορισμένο κύκλο με κέντρο το z=i και ακτίνα 1.
Η σχέση |z1-z2|=2 μας λέει ότι τα z1 και z2 είναι αντιδιαμετρικά.
Άρα μπορούμε να γράψουμε:
z1=z+z0 και z2=z-z0.
Άρα |z1+z2|=|2z|=|2i|=2.
ο.ε.δ.
 .Ωραια αυτη η λυση με τον κυκλο
.Ωραια αυτη η λυση με τον κυκλοΣημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Λήμμα
Αν
Απόδειξη
H
Επιστρέφοντας στην άσκηση λοιπόν, η δεύτερη δοθείσα σχέση γράφεται
απ΄όπου παίρνοντας μέτρα βρίσκουμε ότι
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
soras7
Νεοφερμένο μέλος


Όμορφα, βάζω και το σχήμα.

 .Τα σχηματα που τα φτιαχνεις?????
.Τα σχηματα που τα φτιαχνεις?????Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 14 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 288 μέλη διάβασαν αυτό το θέμα:
- 98.8%chimpanzee
- trifasikodiavasma
- ggl
- ioanna2007
- Hased Babis
- thepigod762
- akis_95
- Mariosm.
- Maynard
- infection54
- Jesse_
- topg
- eukleidhs1821
- bill09876
- Debugging_Demon
- mali
- Joji
- Ness
- Helen06
- Scandal
- synthnightingale
- arko
- BillyTheKid
- Magigi
- Paragontas7000
- Unboxholics
- just some guy
- george777
- Wonderkid
- IceCream05
- Abiogenesis
- GeorgePap2003
- katia.m
- giannhs2001
- paul
- Praxis
- Apocalypse
- shezza94
- desp1naa
- rempelos42
- Sherlockina
- oups
- Dimgeb
- spring day
- KingOfPop
- mpapa
- Chrisa
- Physicsstudent
- tsiobieman
- P.Dam.
- persi
- theodoraooo
- PanosBat
- kost28
- mikriarchitectonissa
- BILL KEXA
- Dr. Gl. Luminous
- Eleftheria2
- Athens2002
- bruh_234
- Miranda32
- SlimShady
- kallikd
- nucomer
- alpha.kappa
- Eeeee
- J.Cameron
- Marple
- Kitana
- F1L1PAS
- sophiaa
- VFD59
- papa2g
- το κοριτσι του μαη
- srg96
- Hopeful22
- Φινεύς
- Phys39
- Anta2004
- fairyelly
- Pharmacist01
- jYanniss
- Panagiotis849
- Kokro
- augustine
- Nikoletaant
- Mashiro@Iberan
- margik
- Mammy Nun
- Pastramis
- Σωτηρία
- Appolon
- panosveki
- Nickt23
- igeorgeoikonomo
- Steliosgkougkou
- QWERTY23
- Ameliak
- aladdin
- nimbus
- Φωτεινη Τζα.
- marian
- Georgekk
- xrisamikol
- the purge
- Theodora03
- Machris
- s93060
- Nikitas18
- Stif6
- stav.mdp
- damn
- aekaras 21
- Anthropaki
- Angelos12345
- ioannam
- Μάρκος Βασίλης
- skyway
- Nick2325
- Nala
- Manolo165
- Ryuzaki
- T C
- Devilshjoker
- El_
- George9989
- TonyMontanaEse
- globglogabgalab
- constansn
- barkos
- katerinavld
- fenia
- An_uknown_world
- Jimmis18
- maria2001
- KingPoul
- Xara
- thecrazycretan
- abcdefg12345
- Κλημεντίνη
- ale
- panagiotis G
- mechaniceng
- Giii
- calliope
- Tequila
- natalix
- Cortes
- Alexecon1991
- pepsoula
- Mariaathens
- Lia 2006
- 1205
- παιδι για κλαματα
- Alexandros36k
- alexd99
- chembam
- Specon
- Dr House
- panagiotis23
- Johnman97
- rhymeasylum
- Αννα Τσιτα
- KaterinaL
- Libertus
- LeoDel
- iminspain
- den antexw allh apotyxia
- Λαμπρινηη
- Mendel2003
- Ijt
- drosos
- Κορώνα
- JohnGreek
- Αρχηγος_β3
- alexandra_
- ΘανάσοςG4
- Dimitris9
- Birtjan
- george7cr7
- NickT
- Bgpanos
- JKTHEMAN
- nicole1982
- χημεια4λαιφ
- Stroka
- Kostakis45
- charmander
- leo41
- EiriniS20
- Αριάνα123
- MarilynSt
- iManosX13
- Nefh_
- Viedo
- Βλα
- suaimhneas
- george pol
- kristinbacktoschool
- fearless
- Rene2004
- Steffie88
- Slytherin
- jimnikol21
- Unseen skygge
- cel123
- jul25
- Thanos_D
- Ireneeneri
- tasost
- Mukumbura
- xxxtolis
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki

