filitsa3
Νεοφερμένο μέλος


ΚΑΙ ΕΚΤΟΣ ΑΠΟ ΟΛΑ ΑΥΤΑ ΔΝ ΞΕΡΩ ΣΕ ΠΟΙΑ ΣΧΟΛΗ ΘΕΛΩ ΠΡΑΓΜΑΤΙΚΑ ΝΑ ΠΕΡΑΣΩΩΩΩΩ
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
coheNakatos
Δραστήριο μέλος


Mπορείτε να με βοηθήσετε με αυτήν εδώ?
Η f είναι δυο φορές παραγωγίσιμη στο(α,β) και η f'' είναι συνεχής.Η γραφική παράσταση της f στο (α,Β τέμνει τον χ'χ στα (ρ1,0) (ρ2,0)με ρ1<ρ2 α)δείξτε οτι υπάρχει ένα τουλάχιστον ρ ανήκει (ρ1,ρ2) τετοιο ώστε f'(ρ)=0 β) f'(ρ1)f'(ρ2)>0 τότε υπάρχει ένα τουλάχιστον χο ανήκει (α,β) ώστε f''(χο)=0
Εστω οτι
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
χρηστοσ17
Νεοφερμένο μέλος


που εχει 4 ριζες πραγματικεσ και ανισες τις ρ1,ρ2,ρ3,ρ4 και (α,β,γ,δ \in R)
α)Ν.Δ.Ο. υπαρχει ενα τουλαχιστον χο,ξ \in (ρ1,ρ4),οπου χο η ριζα τησ τριτης παραγωγου της εξισωσης (ε),ετσι ωστε η συναρτηση φ(ξ)=\frac{1}{2} -\sqrt{2} χο να εχει πραγματικη λυση
β)Ν.Δ.Ο. το σημειο Μ(χο,ξ) ειναι μοναδικο, και να βρεθει η αποσταση του απο την αρχη των αξονων ,αν επιπλεον δινεται οτι το Μ\in στην y=x
γ)Ν.Δ.Ο. υπαρχει ενα τουλαχιστον ω \in R ετσι ωστε η συναρτηση f(x)=-{α}^{2}{χ}^{6}+{α}^{2}{χ}^{3}-8βχ+16χο να εχει πραγματικη λυση ,αν επιπλεον δινεται οτι β<0
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
jimmy007
Εκκολαπτόμενο μέλος


Εστω οτιτοτε (ΑΦΟΥ ΕΙΝΑΙ ΣΥΝΕΧΗΣ προσοχη !) θα διατηρει το προσημο της ,αρα
γν μονοτονη αρα το
του α ερωτηματος ειναι μοναδικο , ευκολα δειχνεις οτι
(αναμεσα ειναι το
) απο υποθεση ατοπο .Αρα υπαρχει
:
=0)
Βαγγέλη στο δεύτερο ερώτημα νομίζω πως έχει κάνει ένα μικρολαθάκι. Πως δείχνεις ότι αν ρ μοναδικό τότε f(r1)f(r2)<0 ?
Ένας άλλος τρόπος που λύνεται το δεύτερο ερώτημα είναι:
Έστω f'(r1)>0, τότε f'(r2)>0. Η f' είναι συνεχής στο r1,r2. Άρα με 2 Θ.Ε.Τ. δείχνεις ότι υπάρχουν r3,r4 στα (r1,r) και (r,r2) αντίστοιχα ώστε f'(r3)=f'(r4). Παίρνεις Rolle στο [r3,r4] και προκύπτει το ζητούμενο.
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
coheNakatos
Δραστήριο μέλος


Βαγγέλη στο δεύτερο ερώτημα νομίζω πως έχει κάνει ένα μικρολαθάκι. Πως δείχνεις ότι αν ρ μοναδικό τότε f(r1)f(r2)<0 ?
Ένας άλλος τρόπος που λύνεται το δεύτερο ερώτημα είναι:
Έστω f'(r1)>0, τότε f'(r2)>0. Η f' είναι συνεχής στο r1,r2. Άρα με 2 Θ.Ε.Τ. δείχνεις ότι υπάρχουν r3,r4 στα (r1,r) και (r,r2) αντίστοιχα ώστε f'(r3)=f'(r4). Παίρνεις Rolle στο [r3,r4] και προκύπτει το ζητούμενο.
το ρ βρισκεται αναμεσα στα ρ1 , ρ2 και f' γν μονοτονη (Δεν εχω κανει ΘΜΤ) Νομιζω πως απανταω πιο συντομα αν δεν εχω λαθος
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
forakos
Νεοφερμένο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Spyros2309
Νεοφερμένο μέλος


Οπότε Αντιπαραγώγιση με άλλα λόγια..
το (ημχ+1)/(συν²χ -2χ +χ²) γράφεται και
-1[(-ημχ - 1)/(συνχ - χ)²]
Ε, γενικά το [1/φ(ψ(χ))]' = -[ψ(χ)]' / [φ(ψ(χ))]²
Παραπάνω δε ξέρω για να βοηθήσω :-)~
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Stavros_ribo
Νεοφερμένο μέλος


Για το β που έχει το ενδιαφέρον, ΘΜΤ για χ1Ε(ρ1,ρ) και χ2Ε(ρ,ρ2)Η f είναι δυο φορές παραγωγίσιμη στο(α,β) και η f'' είναι συνεχής.Η γραφική παράσταση της f στο (α,Β τέμνει τον χ'χ στα (ρ1,0) (ρ2,0)με ρ1<ρ2 α)δείξτε οτι υπάρχει ένα τουλάχιστον ρ ανήκει (ρ1,ρ2) τετοιο ώστε f'(ρ)=0 β) f'(ρ1)f'(ρ2)>0 τότε υπάρχει ένα τουλάχιστον χο ανήκει (α,β) ώστε f''(χο)=0
άρα υπάρχει χ1Ε(ρ1,ρ) ώστε f''(x1)=(f'(ρ)-f'(ρ1))/(ρ-ρ1) δηλ. f''(x1)=-f'(ρ1)/(ρ-ρ1) αντίστοιχα για χ2Ε(ρ,ρ2)
f''(x2)=f'(ρ2)/(ρ2-ρ)
f''(x1)*f''(x2)<0
η f'' συνεχής
Θεώρημα Bolzano άρα υπάρχει τουλ ένα χΕ(χ1,χ2) ώστε f''(x)=0
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
ledzeppelinick
Πολύ δραστήριο μέλος


Μήπως στον παρονομαστη είναι -2χσυνχ???Πως θα υπολογισω αυτο το ολοκληρωμα;
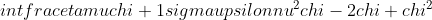
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Metal-Militiaman
Νεοφερμένο μέλος


Πως θα υπολογισω αυτο το ολοκληρωμα;
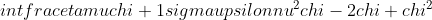
Δεν υπάρχει κάποια μέθοδος να υπολογίσεις το συγκεκριμένο ολοκλήρωμα.Μάλλον κάποιο λάθος έκανες.
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
jimmy007
Εκκολαπτόμενο μέλος


το ρ βρισκεται αναμεσα στα ρ1 , ρ2 και f' γν μονοτονη (Δεν εχω κανει ΘΜΤ) Νομιζω πως απανταω πιο συντομα αν δεν εχω λαθος
Εγώ Θεώρημα Ενδιαμέσων Τιμής χρησιμοποίησα και όχι Θέωρημα Μέση Τιμής.
Μου εξηγείς το πως ακριβώς καταλήγεις σε άτομο??
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
_ann_
Εκκολαπτόμενο μέλος


οταν x τεινει -1..
αν ειχε καπου f(x) και δεν ηξερα αν το οριο της υπαρχει δεν θα μπορουσα αλλα αφου εδω ειναι πολυωνυμικες γιατι να μην μπορω να το λυσω ετσι???
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
ledzeppelinick
Πολύ δραστήριο μέλος


Σωστά τα λες!!:no1:μια απορια...μπορω να σπασω τα ορια?αν οχι γιατι οχι?
οταν x τεινει -1..
αν ειχε καπου f(x) και δεν ηξερα αν το οριο της υπαρχει δεν θα μπορουσα αλλα αφου εδω ειναι πολυωνυμικες γιατι να μην μπορω να το λυσω ετσι???
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
coheNakatos
Δραστήριο μέλος


Εγώ Θεώρημα Ενδιαμέσων Τιμής χρησιμοποίησα και όχι Θέωρημα Μέση Τιμής.
Μου εξηγείς το πως ακριβώς καταλήγεις σε άτομο??
Επειδη υπεθεσα οτι
Επειδη ρ1<ρ<ρ2 (μεσω μονοτονιας )
Αρα
Δεν μπορω να το κανω πιο κατανοητο
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
jimmy007
Εκκολαπτόμενο μέλος


μια απορια...μπορω να σπασω τα ορια?αν οχι γιατι οχι?
οταν x τεινει -1..
αν ειχε καπου f(x) και δεν ηξερα αν το οριο της υπαρχει δεν θα μπορουσα αλλα αφου εδω ειναι πολυωνυμικες γιατι να μην μπορω να το λυσω ετσι???
Σωστό είναι αλλά κάπως φαίνεται. Καλύτερα θα ήταν κατά την γνώμη μου να θέσεις συνάρτηση h.
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
_ann_
Εκκολαπτόμενο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
jimmy007
Εκκολαπτόμενο μέλος


ειναι σωστο ομως?μπορω να το κανω??γιατι πουθενα δεν ειναι λυμμενο ετσι..παντα θετουν..
Δεν μπορώ να σου απαντήσω αυτή την στιγμή με σιγουριά( γιατί νυστάζω αρκετά και δεν σκέφτομαι καθαρά). Το μόνο που μπορώ να σου πω τώρα είναι να δεις το σχολικό βιβλίο γιατί αναφέρεται σε αυτό στην 1.5 ή 1.6 και ουσιαστικά από ότι θυμάμαι απορρίπτει αυτό που έκανες. Για το αν είναι σωστό θα σου απαντήσω άυριο που δεν θα νυστάζω....
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
lowbaper92
Πολύ δραστήριο μέλος


Θεωρώ ότι δεν μπορεις να το σπασεις γιατι αν και υπαρχει το όριο, εχεις 0 στον παρονομαστή και όταν τον στέλνεις (τον παρονομαστή) απο το άλλο μέλος στην ουσία πολλαπλασιαζεις μεμια απορια...μπορω να σπασω τα ορια?αν οχι γιατι οχι?
οταν x τεινει -1..
αν ειχε καπου f(x) και δεν ηξερα αν το οριο της υπαρχει δεν θα μπορουσα αλλα αφου εδω ειναι πολυωνυμικες γιατι να μην μπορω να το λυσω ετσι???
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
blacksheep
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
coheNakatos
Δραστήριο μέλος


μια απορια...μπορω να σπασω τα ορια?αν οχι γιατι οχι?
οταν x τεινει -1..
αν ειχε καπου f(x) και δεν ηξερα αν το οριο της υπαρχει δεν θα μπορουσα αλλα αφου εδω ειναι πολυωνυμικες γιατι να μην μπορω να το λυσω ετσι???
Ενας ασφαλης τροπος ειναι η βοηθητικη συναρτηση
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 21 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 227 μέλη διάβασαν αυτό το θέμα:
- hristosdab
- trifasikodiavasma
- haji
- thepigod762
- Mariosm.
- soulatso
- oteletampis
- phleidhs
- Hased Babis
- AggelikiGr
- sir ImPeCaBlE
- veiNqh
- Scandal
- alekos
- Debugging_Demon
- just some guy
- xristosgkm
- ismember
- Apocalypse
- arrow25
- rempelos42
- ggl
- GStef
- QWERTY23
- xrisamikol
- Σωτηρία
- nikoletaz57
- _Aggelos123
- Mariam38
- SlimShady
- strsismos88
- Georgekk
- Lia 2006
- igeorgeoikonomo
- marian
- tsiobieman
- constansn
- Xristosdimitra
- Panagiotis849
- ρενακι 13
- Memetchi
- eukleidhs1821
- Nikkkpat
- Unboxholics
- korlef
- kwstaseL
- Thanos_D
- the purge
- T C
- Giii
- Papachrist
- liaiscool
- Αννα Τσιτα
- globglogabgalab
- Pharmacist01
- thanahss
- abcdefg12345
- nicole1982
- thecrazycretan
- kvstas92
- KingOfPop
- maria301
- papa2g
- stefan
- Κλημεντίνη
- TonyMontanaEse
- Athens2002
- Alexecon1991
- Μάρκος Βασίλης
- Cortes
- το κοριτσι του μαη
- calliope
- ale
- panagiotis G
- Kleanth
- aggelosst9
- BioChemical
- spring day
- nucomer
- Georgia110
- LeoDel
- pink_panther
- Alexandros973
- marsenis
- den antexw allh apotyxia
- KaterinaL
- kiyoshi
- drosos
- Λαμπρινηη
- Bill22
- Chrysablac.
- giorgosp97
- Βλα
- Monster Hunter
- jul25
- xxxtolis
- Stroka
- nicks1999
- totiloz
- Earendil
- mitsakos
- tasost
- lnesb
- ssalex
- Vasilina93
- alan09
- Livaja10
- χημεια4λαιφ
- Viedo
- UncleJ
- Kostakis45
- Infrared
- Zgian
- pepatogourounaki
- hirasawayui
- GeoCommand
- Eleni54
- American Economist
- EiriniS20
- ΘανάσοςG4
- stamoul1s
- Αριάνα123
- uni77
- Libertus
- tasoss
- PanosCh002
- Unseen skygge
- Νικόλας Ραπ.
- cel123
- The Limit Does Not Exist
- don_vito
- suaimhneas
- Αλκης Κ.
- alexrami
- Baggelitsa36
- Νομικάριος13
- spinalgr1990
- d_th
- Adolfo valencia
- Πα.Κ
- Vasilis25
- Johnman97
- Steffie88
- rekcoR
- gwgw_5
- fockos
- Mariahj
- roud
- kostas83
- Cpt.Philips
- Makis45
- Χρησλου
- Panos_02
- Vold
- tymvorixos
- GiorgosAsi
- Neos167
- theodoraooo
- George187
- Άρτεμις Α.
- Μαρία2222
- christos87
- Idontknoww
- jimis2001
- Metamorph
- Γατόπαρδος.
- Johnsk
- mitsos14
- johnsiak
- Elel
- Dreamer_SW
- Γιαννης1987Θεσσ
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki

