41%
Εκκολαπτόμενο μέλος
Ο 41% αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 25 ετών και Μαθητής Δημοτικού. Έχει γράψει 250 μηνύματα.

24-09-23

17:03
Διάβαζε του Γιάννη και του Δια που είναι διδακτικά, με μεθοδολογία και θα σου χρειαστούν σε όλη τη ζωή σου σχολείο, πανεπιστήμιο κτλ. Αυτά που ανεβάζω εγώ αστα για μεταγενέστερα καθώς είναι προβλήματα πολύ εξειδικευμένα χωρίς μεθοδολογίες και στην παρούσα φάση δεν έχεις να κερδίσεις πολλά. Ουσιαστικά είναι γι' αυτόν που θέλει το κάτι παραπάνω.Για λίγο ειχα αποθαρρυνθεί απο τις θετικές επιστήμες αλλα αυτό εδω το θρέντ μου ξαναξύπνησε το ενδιαφέρον, αν και δεν καταλαβαίνω τιποτα, μου αρέσει να βλέπω και ελπίζω κάποια στιγμή να μπορώ να στείλω και γω κάτι
Dias
Επιφανές μέλος
Ο Dias αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Καθηγητής κι έχει σπουδάσει στο τμήμα Φυσικής ΕΚΠΑ (Αθήνα). Έχει γράψει 10,252 μηνύματα.

25-09-23

11:47
Υ.Γ.2. Καμιά σχέση το LaTex με το Μath Type. Σαφής η υπεροχή του Μath Type.
γιαννης_00
Επιφανές μέλος
Ο γιαννης_00 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 24 ετών, Φοιτητής του τμήματος Πρόγραμμα Ιερατικών Σπουδών και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 12,519 μηνύματα.

25-09-23

14:00
Δια αυτη ειναι μια εξαιρετικη ασηση...μια δυσκολη ασκηση που αν μπει στις πανελληνιες θα κλαψουν παιδια της ιατρικης και του εμπ.
Ειναι μαεστρικη η τοποθετηση των δυναμων τριβης για να αρχισεις να να βγαζεις ακρη..
Και οπα ...μετα το παραξενο κλειδι. Μηπως ειναι λαθος
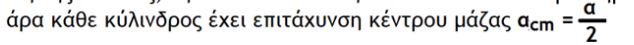
Και ομως ετσι ειναι ..και μετα θυμήθηκα οτι αυτο το ειχα αποδείξει το παλαι ποτε οταν ειχα παροξυσμο λεπτομερειας.
Με την αδεια σου το βαζω εδω και για να το θυμηθω και εγω..
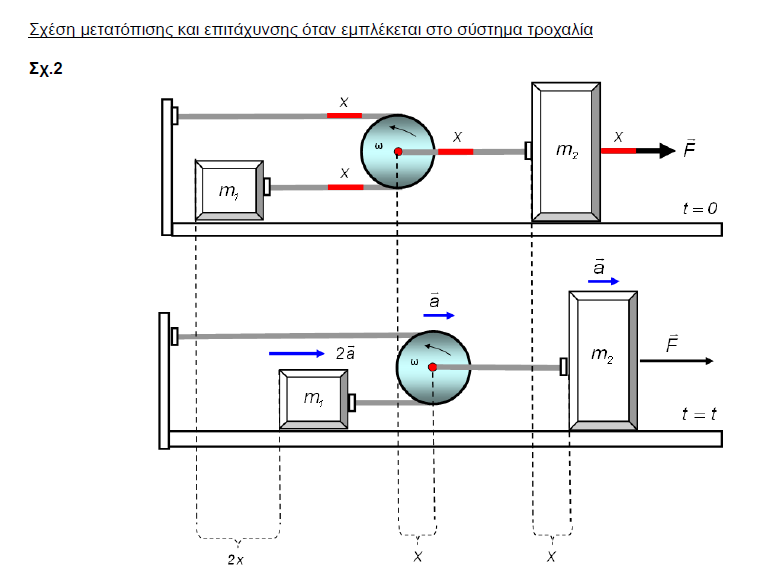

Ειναι μαεστρικη η τοποθετηση των δυναμων τριβης για να αρχισεις να να βγαζεις ακρη..
Και οπα ...μετα το παραξενο κλειδι. Μηπως ειναι λαθος
Και ομως ετσι ειναι ..και μετα θυμήθηκα οτι αυτο το ειχα αποδείξει το παλαι ποτε οταν ειχα παροξυσμο λεπτομερειας.
Με την αδεια σου το βαζω εδω και για να το θυμηθω και εγω..
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11,295 μηνύματα.

25-09-23

14:26
Πρόβλημα :
Οριζόντια ως προς το δάπεδο ακτίνα φωτός προσπίπτει σε ιδανικό καθρέφτη ο οποίος συνδέεται με δεύτερο καθρέφτη κάθετο προς το επίπεδο του πρώτου ( σχηματίζουν γωνία με σχήμα Γ εαν κοιτάξουμε κατακόρυφα προς τα κάτω δηλαδή ) . Τι μπορεί να ειπωθει για την ακτίνα που ανακλάται απο τον δεύτερο καθρέφτη ; Μπορείτε να προτείνετε εφαρμογές αυτού του φαινομένου ;
Οριζόντια ως προς το δάπεδο ακτίνα φωτός προσπίπτει σε ιδανικό καθρέφτη ο οποίος συνδέεται με δεύτερο καθρέφτη κάθετο προς το επίπεδο του πρώτου ( σχηματίζουν γωνία με σχήμα Γ εαν κοιτάξουμε κατακόρυφα προς τα κάτω δηλαδή ) . Τι μπορεί να ειπωθει για την ακτίνα που ανακλάται απο τον δεύτερο καθρέφτη ; Μπορείτε να προτείνετε εφαρμογές αυτού του φαινομένου ;
γιαννης_00
Επιφανές μέλος
Ο γιαννης_00 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 24 ετών, Φοιτητής του τμήματος Πρόγραμμα Ιερατικών Σπουδών και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 12,519 μηνύματα.

25-09-23

14:38
ελα ντε που δεν ασχοληθηκα ποτε με την υπεροχη οπτικηΠρόβλημα :
Οριζόντια ως προς το δάπεδο ακτίνα φωτός προσπίπτει σε ιδανικό καθρέφτη ο οποίος συνδέεται με δεύτερο καθρέφτη που είναι κάθετος στον πρώτο ( σχηματίζουν γωνία με σχήμα Γ εαν κοιτάξουμε κατακόρυφα προς τα κάτω δηλαδή ) . Τι μπορεί να ειπωθει για την ακτίνα που ανακλάται απο τον δεύτερο καθρέφτη ; Μπορείτε να προτείνετε εφαρμογές αυτού του φαινομένου ;
αυτη ειναι η βασικη αρχη που δουλευουν τα μεγαλα τηλεσκοπια με τεραστια μεγενθυνση και οι φωτογραφικοι φακοι υψηλής ποιοτητας
Αστειο
Απο εδω που ειμαι βλεπω κατα τις 7 η ωρα να αναβουν προβολεις στους δρομους της ανω γλυφαδας... μετα απο κανενα μισαωρο σβηνουν ,,ειναι οι ανακλασεις του ηλιου στους ασημενιους ηλιακους
Και επι του πρακτεου
Το ξενοδοχειο king George στο συνταγμα εχει ενα εσωτερικο κουφιο πηρηνα οπου βλεπουν τα εσωτερικα παράθυρα και τα εσωτερικα μπαλκονια των δωματιων.
Επειδη δεν εχει μεγαλη διαμετρο και το ηλιακο φως δεν φτανει ..τον φωτιζουν με ανακλαση καθρεπτων του ηλιακου φωτος... που ειναι στην ταρατσα και μαλιστα με κινηση ακολουθουν την πορεια του ηλιου.
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11,295 μηνύματα.

25-09-23

15:00
Η αλήθεια δυστυχώς είναι οτι την οπτική το σχολείο την έχει ακόμα πιο γραμμένη και απο την θερμοδυναμική .ελα ντε που δεν ασχοληθηκα ποτε με την υπεροχη οπτικη
αυτη ειναι η βασικη αρχη που δουλευουν τα μεγαλα τηλεσκοπια με τεραστια μεγενθυνση και οι φωτογραφικοι φακοι υψηλής ποιοτητας
Αστειο
Απο εδω που ειμαι βλεπω κατα τις 7 η ωρα να αναβουν προβολεις στους δρομους της ανω γλυφαδας... μετα απο κανενα μισαωρο σβηνουν ,,ειναι οι ανακλασεις του ηλιου στους ασημενιους ηλιακους
Και επι του πρακτεου
Το ξενοδοχειο king George στο συνταγμα εχει ενα εσωτερικο κουφιο πηρηνα οπου βλεπουν τα εσωτερικα παράθυρα και τα εσωτερικα μπαλκονια των δωματιων.
Επειδη δεν εχει μεγαλη διαμετρο και το ηλιακο φως δεν φτανει ..τον φωτιζουν με ανακλαση καθρεπτων του ηλιακου φωτος... που ειναι στην ταρατσα και μαλιστα με κινηση ακολουθουν την πορεια του ηλιου.
Το οποίο αφενός με θλίβει προσωπικά γιατί εαν και όλοι οι τομείς της φυσικής είναι τρομεροί , ομολογώ οτι εδώ έχω λίγη παραπάνω αδυναμία , και αφετέρου επειδή το φως και όσες τεχνολογίες βασίζονται σε αυτό είναι τόσο αναπόσπαστο μέρος του σύγχρονου κόσμου που μου φαίνεται αδιανόητο να μην διδάσκονται βασικά πράγματα . Δηλαδή δεν μπορεί να πιάσει κανείς ούτε έναν κλάδο ο οποίος δεν έχει επωφεληθεί τρομερά απο την οπτική και την φωτονική .
Και δεν θα πάω πολύ μακριά , το πιο άμεσο παράδειγμα ενδεχομένως είναι η οπτική ίνα , χωρίς την οποία το internet δεν θα ήταν ούτε κατά διάννοια στο σημείο που είναι σήμερα , για να μιλάμε για τόσο τρομακτικά τεράστιους ρυθμούς μετάδοσης .
Υ.Γ. συνήθως δεν βάζω λύσεις , όμως στο συγκεκριμένο θα βάλω . Απλά προτού το επιχειρήσω καλό θα ήταν να το προσπαθήσει κανείς , βγαίνει σε 2 γραμμές , είναι το πιο εύκολο πιστεύω που έχω βάλει ως σήμερα και το αποτέλεσμα είναι ιδιαίτερα ενδιαφέρον!
γιαννης_00
Επιφανές μέλος
Ο γιαννης_00 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 24 ετών, Φοιτητής του τμήματος Πρόγραμμα Ιερατικών Σπουδών και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 12,519 μηνύματα.

25-09-23

15:04
Σωστα... ειδες μια πετονια τι κανει ..πολυ περισσοτερο απο το να πιανει σπαρουςΗ αλήθεια δυστυχώς είναι οτι την οπτική το σχολείο την έχει ακόμα πιο γραμμένη και απο την θερμοδυναμική .
Το οποίο αφενός με θλίβει προσωπικά γιατί εαν και όλοι οι τομείς της φυσικής είναι τρομεροί , ομολογώ οτι εδώ έχω λίγη παραπάνω αδυναμία , και αφετέρου επειδή το φως και όσες τεχνολογίες βασίζονται σε αυτό είναι τόσο αναπόσπαστο μέρος του σύγχρονου κόσμου που μου φαίνεται αδιανόητο να μην διδάσκονται βασικά πράγματα . Δηλαδή δεν μπορεί να πιάσει κανείς ούτε έναν κλάδο ο οποίος δεν έχει επωφεληθεί τρομερά απο την οπτική και την φωτονική .
Και δεν θα πάω πολύ μακριά , το πιο άμεσο παράδειγμα ενδεχομένως είναι η οπτική ίνα , χωρίς την οποία το internet δεν θα ήταν ούτε κατά διάννοια στο σημείο που είναι σήμερα , για να μιλάμε για τόσο τρομακτικά τεράστιους ρυθμούς μετάδοσης .
Υ.Γ. συνήθως δεν βάζω λύσεις , όμως στο συγκεκριμένο θα βάλω . Απλά προτού το επιχειρήσω καλό θα ήταν να το προσπαθήσει κανείς , βγαίνει σε 2 γραμμές , είναι το πιο εύκολο πιστεύω που έχω βάλει ως σήμερα και το αποτέλεσμα είναι ιδιαίτερα ενδιαφέρον!
γιαννης_00
Επιφανές μέλος
Ο γιαννης_00 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 24 ετών, Φοιτητής του τμήματος Πρόγραμμα Ιερατικών Σπουδών και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 12,519 μηνύματα.

25-09-23

19:09
Αυτόματη ένωση συνεχόμενων μηνυμάτων:
Αυτόματη ένωση συνεχόμενων μηνυμάτων:
εγω τι να μπλεξω ..τιποτα,,μα δεν βλεπεις οτι ο μαθηματικουλης θελεις να μας παρει τα διανυσματα ,,θα τον αφησω,,, θα του ριξω μπολικα και ας ειναι και απο στροβιλο πεδιοΠως τα εμπλέξες ρε'συ αυτά τα δύο δεν έχουν καμία σχέση αυτά τα δύο
Εγώ σκεφτόμουν τώρα κάτι αλλά δεν ξέρω εάν στέκει . Εάν θεωρούσαμε συνάρτηση απο το Ν* στο Ν^2 με Df = [1, 2ν(2μ +1)] και f(1) = (1,1) , f( 2ν(2μ+1) ) = (2μ+1,1) και δείχναμε ότι δεν μπορεί να είναι 1-1 .
Dias
Επιφανές μέλος
Ο Dias αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Καθηγητής κι έχει σπουδάσει στο τμήμα Φυσικής ΕΚΠΑ (Αθήνα). Έχει γράψει 10,252 μηνύματα.

25-09-23

19:55
Χμμμμ... Πήρε το μάτι μου ότι κάποια παιδάκια θέλουν άσκηση Οπτικής. Ο θείος Δίας δεν χαλά χατίρια. Απολαύστε μία αγαπημένη. Πάντως, γενικά ο κόσμος δεν αγαπά την Οπτική γιατί κρύβει μέσα της τη Γεωμετρία. Δηλαδή χρειάζονται βασικές γνώσεις Γεωμετρίας και το σχήμα πρέπει να είναι άψογο και λεπτομερές. Καλή διασκέδαση...

ΛΥΣΗ
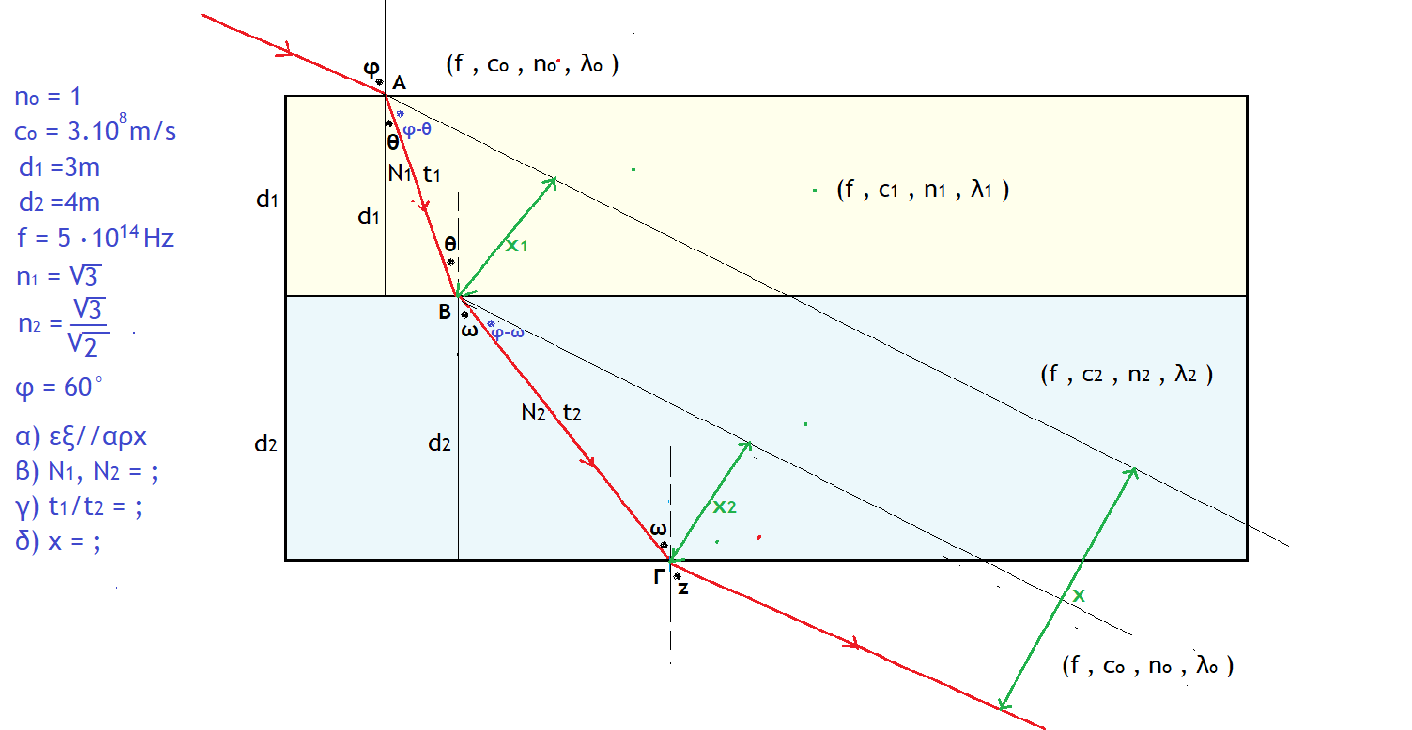

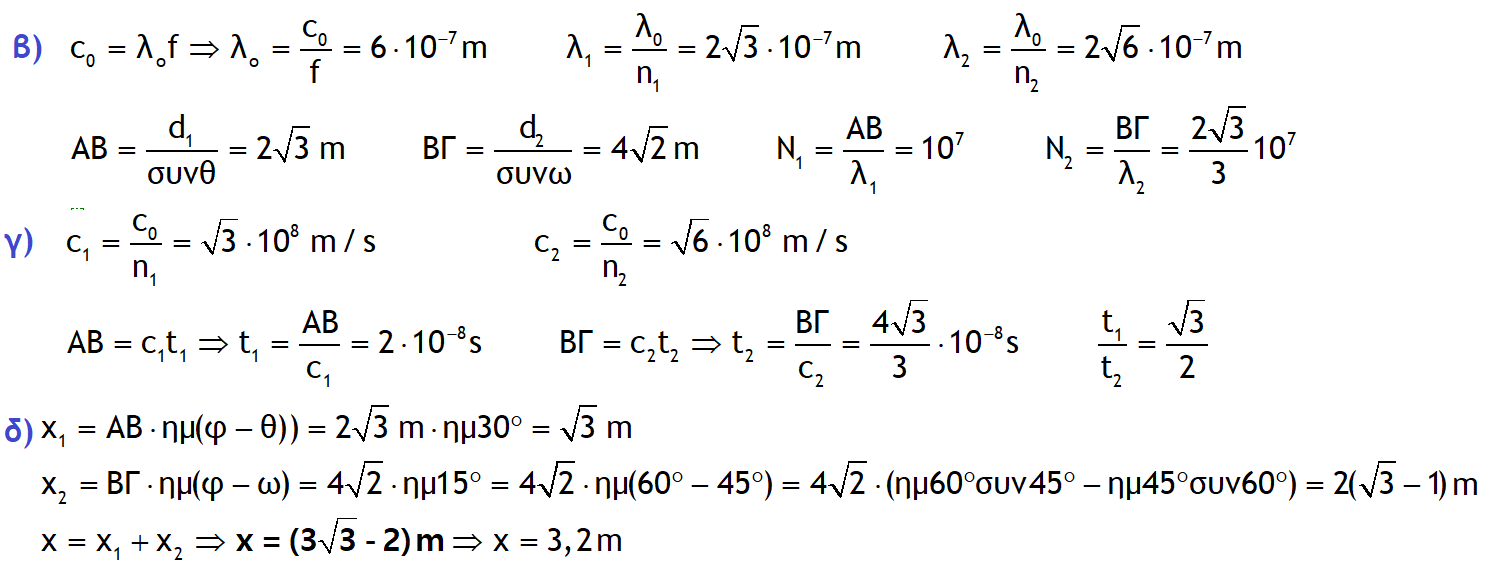

ΛΥΣΗ
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11,295 μηνύματα.

25-09-23

23:13
Πρόβλημα :
Οριζόντια ως προς το δάπεδο ακτίνα φωτός προσπίπτει σε ιδανικό καθρέφτη ο οποίος συνδέεται με δεύτερο καθρέφτη κάθετο προς το επίπεδο του πρώτου ( σχηματίζουν γωνία με σχήμα Γ εαν κοιτάξουμε κατακόρυφα προς τα κάτω δηλαδή ) . Τι μπορεί να ειπωθει για την ακτίνα που ανακλάται απο τον δεύτερο καθρέφτη ; Μπορείτε να προτείνετε εφαρμογές αυτού του φαινομένου ;
Το αποτέλεσμα δείχνει οτι η προσπίπτουσα ακτίνα επιστρέφει απο την διάταξη των δύο καθρεφτών πίσω στην πηγή ανεξάρτητα απο την γωνία που προσπίπτει αρχικά στους καθρέφτες . Αυτό με έναν μόνο καθρέφτη δεν μπορεί να γίνει . Προσθέτωντας έναν τρίτο καθρέφτη , κάθετο στους δύο προηγούμενους ,η ακτίνα μπορεί μάλιστα να πέσει υπό οποιαδήποτε κατεύθυνση στην διάταξη και να επιστέψει επίσης πίσω στην πηγή ( μετατοπισμένη φυσικά ) .
Διατάξεις που αξιοποιούν αυτή την γεωμετρία έχουν τοποθετηθεί για παράδειγμα στο φεγγάρι έτσι ώστε να μπορούμε να μετρήσουμε την απόσταση της απο την Γη ( σκοπεύοντας την με laser και μετρώντας το ανακλώμενο φως ) . Σημαντικές εφαρμογές υπάρχουν όμως και στον στρατιωτικό τομέα . Πολλαπλές ανακλάσεις απο τις λείες επιφάνειες ενός αεροσκάφους μπορούν να οδηγήσουν το προσπίτων ηλεκτρομαγνητικό κύμα απο ένα ραντάρ πίσω στον δέκτη του , οπότε η ραδιοδιατομή του στόχου εμφανίζεται μεγαλύτερη απο οτι είναι κανονικά . Αυτό μπορεί να είναι και καλό και κακό . Για παράδειγμα εαν ο σκοπός του αεροσκάφους είναι να αφήνει μικρό ίχνος στην οθόνη του ραντάρ , τότε είναι κακό . Μπορεί όμως να αξιοποιηθεί σκόπιμα κιόλας αυτό το φαινόμενο έτσι ώστε μικροί στόχοι όπως πύραυλοι για παράδειγμα να παίξουν τον ρόλο της παραπλάνησης , και τα εχθρικά ραντάρ να νομίζουν οτι βλέπουν κάποιο μεγάλο αεροπλάνο .
Αυτόματη ένωση συνεχόμενων μηνυμάτων:
Πολύ ωραίο σχήμα Δία . Και πολύ διδακτικό πρόβλημα ! Ίσως ανεβάσω αργότερα εαν προλάβω ένα παρόμοιας φύσεως το οποίο θα σχετίζεται με τον ήχο .Χμμμμ... Πήρε το μάτι μου ότι κάποια παιδάκια θέλουν άσκηση Οπτικής. Ο θείος Δίας δεν χαλά χατίρια. Απολαύστε μία αγαπημένη. Πάντως, γενικά ο κόσμος δεν αγαπά την Οπτική γιατί κρύβει μέσα της τη Γεωμετρία. Δηλαδή χρειάζονται βασικές γνώσεις Γεωμετρίας και το σχήμα πρέπει να είναι άψογο και λεπτομερές. Καλή διασκέδαση...
View attachment 122682
ΛΥΣΗ
Η γεωμετρία όντως δυσκολεύει πολύ κόσμο στην οπτική . Κακά τα ψέματα τα οπτικά φαινόμενα εαν και περιγράφονται απο πολύ απλούς νόμους ( όπως αυτούς της ανάκλασης , του snell κτλπ. ) ως προς την μαθηματική διατύπωση , δεν παύουν να είναι τρομερά πολύπλοκα φαινόμενα .
41%
Εκκολαπτόμενο μέλος
Ο 41% αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 25 ετών και Μαθητής Δημοτικού. Έχει γράψει 250 μηνύματα.

26-09-23

15:46
Αν κλαίνε και στο εμπ με προβλήματα φυσικής κοίτα να πας σε άλλο πολυτεχνείο.θα κλαψουν παιδια της ιατρικης και του εμπ
Δεν έχουμε να κάνουμε φυσική εναντίον μαθηματικά το καθένα εξυπηρετεί άλλα πράγματα. Τα διανύσματα πάντως είναι καθαρά μαθηματικό εργαλείο που εφαρμόζεται σε πλήθος από επιστήμες.εγω τι να μπλεξω ..τιποτα,,μα δεν βλεπεις οτι ο μαθηματικουλης θελεις να μας παρει τα διανυσματα ,,θα τον αφησω,,, θα του ριξω μπολικα και ας ειναι και απο στροβιλο πεδιο
Θείε Δία, όπως γράφει από πάνω και ο johnny ούτε εγώ έχω ασχοληθεί με οπτική, αλλά βρίσκω ενδιαφέρον το πρόβλημα που ανέβασες και πιθανές εφαρμογές, αν έχεις τίποτα καλό ρίχτο να μάθουμε και κάτι καινούριο.Πήρε το μάτι μου ότι κάποια παιδάκια θέλουν άσκηση Οπτικής. Ο θείος Δίας δεν χαλά χατίρια.
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11,295 μηνύματα.

26-09-23

20:34
@γιαννης_00 αυτό πιστεύω θα σου αρέσει . Απλό πρόβλημα αλλά με βαθύ νόημα και θεωρία απο πίσω με ευρύτατες εφαρμογές .
Πρόβλημα :
Χρησιμοποιούμε λαμπτήρα τον οποίο αναβοσβήνουμε με συχνότητα Fo . Δίπλα μας τοποθετούμε τροχό ο οποίος περιστρέφεται αριστερόστροφα ( απο την δική μας γωνία θέασης ) με συχνότητα fo . Ο δίσκος έχει μια κόκκινη γραμμή ζωγραφισμένη πάνω του που συνδέει την άκρη του με το κέντρο του . Αρχικά η κόκκινη γραμμή πάνω στον δίσκο είναι παράλληλη προς το έδαφος . Τι θα παρατηρήσουμε ανάλογα με την σχέση μεταξύ των fo και Fo ; Θεωρούμε οτι ο λαμπτήρας ανάβει και σβήνει σχεδόν ακαριαία .
Πρόβλημα :
Χρησιμοποιούμε λαμπτήρα τον οποίο αναβοσβήνουμε με συχνότητα Fo . Δίπλα μας τοποθετούμε τροχό ο οποίος περιστρέφεται αριστερόστροφα ( απο την δική μας γωνία θέασης ) με συχνότητα fo . Ο δίσκος έχει μια κόκκινη γραμμή ζωγραφισμένη πάνω του που συνδέει την άκρη του με το κέντρο του . Αρχικά η κόκκινη γραμμή πάνω στον δίσκο είναι παράλληλη προς το έδαφος . Τι θα παρατηρήσουμε ανάλογα με την σχέση μεταξύ των fo και Fo ; Θεωρούμε οτι ο λαμπτήρας ανάβει και σβήνει σχεδόν ακαριαία .
Dias
Επιφανές μέλος
Ο Dias αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Καθηγητής κι έχει σπουδάσει στο τμήμα Φυσικής ΕΚΠΑ (Αθήνα). Έχει γράψει 10,252 μηνύματα.

26-09-23

21:37
Κλασικό στροβοσκόπιο.Χρησιμοποιούμε λαμπτήρα τον οποίο αναβοσβήνουμε με συχνότητα Fo . Δίπλα μας τοποθετούμε τροχό ο οποίος περιστρέφεται αριστερόστροφα ( απο την δική μας γωνία θέασης ) με συχνότητα fo . Ο δίσκος έχει μια κόκκινη γραμμή ζωγραφισμένη πάνω του που συνδέει την άκρη του με το κέντρο του . Αρχικά η κόκκινη γραμμή πάνω στον δίσκο είναι παράλληλη προς το έδαφος . Τι θα παρατηρήσουμε ανάλογα με την σχέση μεταξύ των fo και Fo ; Θεωρούμε οτι ο λαμπτήρας ανάβει και σβήνει σχεδόν ακαριαια
Αν Fo = fo η γραμμή θα φαίνεται ακίνητη
Αν Fo < fo η γραμμή θα φαίνεται να κινείται αργά αριστερόστροφα
Αν Fo > fo η γραμμή θα φαίνεται να κινείται αργά δεξιόστροφα
Έχω ένα παλιό πικάπ που ελέγχω αν γυρίζει σωστά συγκρίνοντας τη συχνότητα περιστροφής με αυτή του εναλλασσόμενου ρεύματος.
Η στροβοσκοπική μέθοδος είναι πολύ συνηθισμένη στα συνεργεία αυτοκινήτων και σε πολλούς τομείς της βιομηχανίας.
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11,295 μηνύματα.

26-09-23

22:50
Ακριβώς Δία !Κλασικό στροβοσκόπιο.
Αν Fo = fo η γραμμή θα φαίνεται ακίνητη
Αν Fo < fo η γραμμή θα φαίνεται να κινείται αργά αριστερόστροφα
Αν Fo > fo η γραμμή θα φαίνεται να κινείται αργά δεξιόστροφα
Έχω ένα παλιό πικάπ που ελέγχω αν γυρίζει σωστά συγκρίνοντας τη συχνότητα περιστροφής με αυτή του εναλλασσόμενου ρεύματος.
Η στροβοσκοπική μέθοδος είναι πολύ συνηθισμένη στα συνεργεία αυτοκινήτων και σε πολλούς τομείς της βιομηχανίας.
Το πρόβλημα έχει και μια πολύ σοβαρή εφαρμογή στον φωτισμό χώρων που χρησιμοποιούν λαμπτήρες φθορισμού . Επειδή η τάση απο το δίκτυο μηδενίζεται δύο φορές σε μια περίοδο ( και η συχνότητα της εναλασσόμενης τάσης του δικτύου είναι 50 Hz ) , η τάση μηδενίζεται με συχνότητα 100 Hz . Εξοπλισμός που έχει στρεφόμενα μέρη τα οποία περιστρέφονται σε αρμονικές των 100 Hz λοιπόν ( π.χ. 200Hz , 300Hz...1000Hz κτλπ.) φαίνονται να είναι ακίνητα ή να κινούνται πολύ αργά . Αυτό μπορεί να οδηγήσει σε ατύχημα . Για αυτό ο ηλεκτρολόγος που κάνει μια μελέτη φωτισμού θα πρέπει να είναι πολύ προσεκτικός σε τέτοια θέματα διότι αφορούν την ασφάλεια .
Συνήθως ο τρόπος που αντιμετωπίζεται αυτό το πρόβλημα είναι είτε η τροφοδοσία με συνεχές ρεύμα , είτε η οδήγηση των λαμπτήρων με κατάλληλη συχνότητα , είτε με τριφασική παροχή , έτσι ώστε όταν μια φάση μηδενίζεται , να μην μηδενίζεται γενικά η τάση .
Υπάρχει μάλιστα ένα πολύ ενδιαφέρον και πολύ θεμελιώδες ζήτημα που κρύβεται σε αυτό το πρόβλημα . Στην ουσία η διακοπή του φωτός με συχνότητα Fo , κυριολεκτικά μας εξαναγκάζει να "δειγματοληπτούμε" την θέση της κόκκινης ρίγας ( η οποία στην ουσία μας "προδίδει" κατά κάποιο τρόπο την γωνιακή περιστροφή του δίσκου ) με συχνότητα Fo . Εαν σας βοηθάει σκεφτείτε οτι η δειγματοληψία είναι σαν κάποιος να σας ζητάει να έχετε κλειστά τα μάτια σας και να τα ανοίγετε κάθε 1/Fo δευτερόλεπτα για να παρατηρείτε που είναι η κόκκινη ρίγα .
Ένα βασικό θεώρημα στην επεξεργασία σημάτων , αυτό του Shannon λέεπ πως όταν δειγματοληπτείς ένα σήμα με συχνότητα μικρότερη απο το διπλάσιο της μεγαλύτερης συχνότητας που περιέχει , είναι αδύνατο να ανακατασκευάσεις το αρχικό σήμα . Δηλαδή μας είναι αδύνατο να προσδιορίσουμε την συχνότητα περιστροφής του δίσκου εαν Fo < 2fo .
Τι σημαίνει αυτό για τα μάτια μας όμως ; Σημαίνει οτι εκλαμβάνουμε λανθασμένα την συχνότητα περιστροφής του δίσκου λόγω της εμφάνισης του φαινομένου της αναδίπλωσης ή αλλοίωσης . Αντιλαμβανόμαστε δηλαδή λανθασμένη συχνότητα σε σχέση με την πραγματική που περιέχει το σήμα μας . Και συγκεκριμένα σε αυτό το πρόβλημα , όχι απλώς εκλαμβάνουμε λανθασμένα την πραγματική συχνότητα περιστροφής του δίσκου , αλλά εκλαμβάνουμε λανθασμένα ακόμα και την φορά περιστροφής του , όπως επισήμανε ο Δίας !
Για παράδειγμα εαν Fo = 1/(3/4)T = 4fo/3 , δηλαδή ο λαμπτήρας ανάβει ακαριαία με συχνότητα Fo = 4fo/3 > fo , βλέπουμε αρχικά την κόκκινη ρίγα στην θέση 0°( οριζόντια με το δάπεδο και φορά δεξιά) , μετά σε θέση 270° ( κατακόρυφη με φορά προς τα κάτω ) , μετά πάλι στην θέση 0° , μετά στην θέση 90° ( κατακόρυφη με φορά προς τα πάνω ) κ.ο.κ. Η μαύρη γραμμή είναι η πραγματική θέση της ρίγας συναρτήσει του χρόνου . Οι κόκκινες γραμμές αντιστοιχούν στις στιγμές που ο λαμπτήρας ανάβει και εντοπίζουμε την ρίγα . Η πράσσινη καμπύλη αντιστοιχή στην κίνηση της ρίγας όπως την καταλαβαίνουμε εμείς ως παρατηρητές . Όπως είναι φανερό , νομίζουμε οτι η κόκκινη ρίγα κινείται δεξιόστροφα , και όχι αριστερόστροφα !
Απο την άλλη εαν Fo = fo , η κόκκινη ρίγα όπως φαίνεται , παρατηρείται συνεχώς στην θέση θ = 0° , οπότε δεν καταλαβαίνουμε οτι έχει μετακινηθεί .
Fun fact : Όσοι είστε gamers θα έχετε παρατηρήσει μια ρύθμιση που ονομάζεται anti-aliasing filtering στις ρυθμίσεις γραφικών των παιχνιδιών σας . Ίσως να μην ξέρετε τι ακριβώς κάνει αυτή η ρύθμιση αλλά σίγουρα θα έχετε καταλάβει οτι όταν το ενεργοποιείτε , τα γραφικά που αφορούν ακμές για παράδειγμα γίνονται αισθητικά πιο όμορφα . Σίγουρα θα έχετε παρατηρήσει όμως και οτι ο υπολογιστή σας ζορίζεται παραπάνω σε σχέση με πριν . Τι ακριβώς συμβαίνει ;
Επί της ουσίας ακριβώς το ίδιο φαινόμενο που συζητήσαμε παραπάνω υπάρχει και στο παιχνίδι σας . Η διαφορά εδώ είναι οτι αυτό το φαινόμενο της αναδίπλωσης συμβαίνει στον χώρο πλέον και όχι στον χρόνο . Η σκηνή του παιχνιδιού σας ενδέχεται να απεικονίζει φυσικά αντικείμενα τα οποία χωρικά έχουν μεγάλη επανάληψη στοιχείων/μοτίβων ( λόγου χάρη ένας φράχτης ή ένας τοίχος απο τούβλα ) . Όταν η χωρική συχνότητα επανάληψης αυτών των στοιχείων είναι πολύ μεγάλη , με αποτέλεσμα μια χωρική εναλλαγή να είναι τόσο γρήγορη ώστε να χάνεται μεταξύ γειτονικών pixels , η εικόνα χαλάει . Ένας τρόπος να διορθωθεί το πρόβλημα είναι η αύξηση της ανάλυσης της οθόνης ( θυμηθείτε , πιο πυκνό πλέγμα απο pixel σημαίνει οτι δειγματοληπτείτε την πραγματική εικόνα με μεγαλύτερη χωρική συχνότητα ) . Μια άλλη λύση όμως είναι η ενεργοποίηση της περίφημης ρύθμισης του anti-aliasing φίλτρου . Αυτό , αντί να αυξήσει την συχνότητα που δειγματοληπτούμε την εικόνα για να την παρουσιάσουμε στον χρήστη μέσω της οθόνης , προσπαθεί να ξεφορτωθεί αυτές τις υψηλές χωρικές συχνότητες . Αυτό πρέπει να παραδεχτούμε οτι ακούγεται πολύ πιο λογικό καθώς αύξηση της ανάλυσης της οθόνης σημαίνει μεγαλύτερη απαιτούμενη επεξεργαστική ισχύ , και δεν συμφέρει τόσο δεδομένου οτι το πρόβλημα υπάρχει μόνο σε συγκεκριμένα μέρη της εικόνας που βλέπουμε . Υπάρχει κάποιο μειονέκτημα ; Φυσικά και υπάρχει . Όταν πετάς αυτή την υψίσυχνη πληροφορία , ενώ βελτιώνεις αισθητικά την εικόνα που βλέπεις στην οθόνη , ταυτόχρονα έχεις χάσει λεπτομέρειες και ακρίβεια . Κοινώς προκαλείς μια "θολούρα" .
Ελπίζω να ήταν κάπως ενδιαφέρον πρόβλημα !
Cade
Πολύ δραστήριο μέλος
Ο Cade αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Απόφοιτος λυκείου. Έχει γράψει 851 μηνύματα.

26-09-23

22:52
Έστω 2 φορές παραγωγίσιμη συνάρτηση f στο [0, +00), με f(0)=0 και f(x)>0 για κάθε x>0.
Αν η f έχει μοναδικό σημείο καμπής στο x=α >0 και
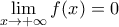
να δείξετε ότι υπάρχει bε(0,α) στο οποίο παίρνει τη μέγιστη τιμή της.
Αν η f έχει μοναδικό σημείο καμπής στο x=α >0 και
να δείξετε ότι υπάρχει bε(0,α) στο οποίο παίρνει τη μέγιστη τιμή της.
Dias
Επιφανές μέλος
Ο Dias αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Καθηγητής κι έχει σπουδάσει στο τμήμα Φυσικής ΕΚΠΑ (Αθήνα). Έχει γράψει 10,252 μηνύματα.

27-09-23

19:34
ΛΥΣΗ
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11,295 μηνύματα.

28-09-23

05:30
Θα πρότεινα την εξής λύση :Έστω 2 φορές παραγωγίσιμη συνάρτηση f στο [0, +00), με f(0)=0 και f(x)>0 για κάθε x>0.
Αν η f έχει μοναδικό σημείο καμπής στο x=α >0 και
View attachment 122775
να δείξετε ότι υπάρχει bε(0,α) στο οποίο παίρνει τη μέγιστη τιμή της.
Η f είναι συνεχής στο [0,α] , οπότε απο το ΘΜΕΤ θα παίρνει μια ελάχιστη και μια μέγιστη τιμή σε αυτό το διάστημα . Ξέρουμε οτι f(x) > 0 για κάθε χ > 0 και οτι f(0) = 0 . Οπότε το 0 είναι σημείο ελαχίστου .
Ας υποθέσουμε οτι το χ = α είναι το σημείο μεγίστου . Σε αυτή την περίπτωση επειδή η f είναι παραγωγίσιμη , και παρουσιάζει ακρότατο στο α , το οποίο είναι εσωτερικό σημείο του πεδίου ορισμού , θα ισχύει απο το Θ.Fermat :
f'(α) = 0
Το α όμως είναι το μοναδικό σημείο καμπής . Οπότε αυτό σημαίνει οτι η f αλλάζει κυρτότητα εκατέρωθεν του α.
Απο το ΘΜΤ για την f στο [0,α] θα υπάρχει ξ Ε (0,α) :
f'(ξ) = f(α)/α , το οποίο είναι θετικό καθώς α > 0 και f(x) > 0 για κάθε χ > 0 .
Έτσι έχουμε ξ < α , με f'(ξ) > f'(α) = 0
Δηλαδή η f' είναι γνησίως φθίνουσα στο [0,α] και γνησίως αύξουσα για χ > α .
Απο το ΘΜΤ όμως για την f στο [α,χ] , υπάρχει ζ Ε (α,χ) :
f'(ζ) = [ f(χ) - f(α) ]/(χ - α)
Εφόσον ζ > α θα πρέπει να ισχύει το εξής εφόσον η f' είναι γνησίως αύξουσα για χ > α :
f'(ζ) > f'(α) = 0 =>
[ f(χ) - f(α) ]/(χ - α) > 0 =>
lim { [ f(χ) - f(α) ]/(χ - α) } > 0 =>
x->+oo
0 > 0
Άτοπο.
Άρα το μέγιστο του διαστήματος [0,α] θα παρουσιάζεται σε κάποια θέση b E (0,α) .
Επιπλέον δεν μπορεί να υπάρχει κάποιο μέγιστο για χ > α , διότι εφόσον το α είναι το μοναδικό σημείο καμπής , η f θα είναι είτε κοίλη είτε κυρτή στο (0,α) . Εφόσον το α είναι μέγιστο , η f θα είναι κοίλη στο (0,α) και επομένως κυρτή στο (α,+οο)*.
Δηλαδή η f' είναι γνησίως φθίνουσα στο (0,α] και γνησίως αύξουσα στο [α,+οο) . Οπότε :
x > α =>
f'(x) > f'(α) = 0
Εαν υπήρχε όντως κάποιο μέγιστο στην θέση χο Ε (α,+οο) , τότε απο το θ.Fermat θα ίσχυε :
f'(xo) = 0 , το οποίο είναι άτοπο καθώς μόλις πριν δείξαμε οτι είναι f'(χ) > 0 , για κάθε χ > α .
*Αυτό μπορεί να δειχθεί εύκολα . Εαν η f ήταν κυρτή στο (0,α) και είχε μέγιστο στο x = b Ε (0,α) , τότε θα ίσχυε για κάθε χ Ε (0,α):
f(x) >= f(b) + f'(b)(x - b) = f(b) => λόγω Θ.Fermat
f(x) >= f(b)
Το οποίο είναι άτοπο καθώς το f(b) είναι το μέγιστο , οπότε θα έπρεπε f(x) <= f(b) . Άρα η f είναι κοίλη στο (0,α).
Εν τέλει λοιπόν το b E (0,α) είναι το μέγιστο της f .
Ας υποθέσουμε οτι το χ = α είναι το σημείο μεγίστου . Σε αυτή την περίπτωση επειδή η f είναι παραγωγίσιμη , και παρουσιάζει ακρότατο στο α , το οποίο είναι εσωτερικό σημείο του πεδίου ορισμού , θα ισχύει απο το Θ.Fermat :
f'(α) = 0
Το α όμως είναι το μοναδικό σημείο καμπής . Οπότε αυτό σημαίνει οτι η f αλλάζει κυρτότητα εκατέρωθεν του α.
Απο το ΘΜΤ για την f στο [0,α] θα υπάρχει ξ Ε (0,α) :
f'(ξ) = f(α)/α , το οποίο είναι θετικό καθώς α > 0 και f(x) > 0 για κάθε χ > 0 .
Έτσι έχουμε ξ < α , με f'(ξ) > f'(α) = 0
Δηλαδή η f' είναι γνησίως φθίνουσα στο [0,α] και γνησίως αύξουσα για χ > α .
Απο το ΘΜΤ όμως για την f στο [α,χ] , υπάρχει ζ Ε (α,χ) :
f'(ζ) = [ f(χ) - f(α) ]/(χ - α)
Εφόσον ζ > α θα πρέπει να ισχύει το εξής εφόσον η f' είναι γνησίως αύξουσα για χ > α :
f'(ζ) > f'(α) = 0 =>
[ f(χ) - f(α) ]/(χ - α) > 0 =>
lim { [ f(χ) - f(α) ]/(χ - α) } > 0 =>
x->+oo
0 > 0
Άτοπο.
Άρα το μέγιστο του διαστήματος [0,α] θα παρουσιάζεται σε κάποια θέση b E (0,α) .
Επιπλέον δεν μπορεί να υπάρχει κάποιο μέγιστο για χ > α , διότι εφόσον το α είναι το μοναδικό σημείο καμπής , η f θα είναι είτε κοίλη είτε κυρτή στο (0,α) . Εφόσον το α είναι μέγιστο , η f θα είναι κοίλη στο (0,α) και επομένως κυρτή στο (α,+οο)*.
Δηλαδή η f' είναι γνησίως φθίνουσα στο (0,α] και γνησίως αύξουσα στο [α,+οο) . Οπότε :
x > α =>
f'(x) > f'(α) = 0
Εαν υπήρχε όντως κάποιο μέγιστο στην θέση χο Ε (α,+οο) , τότε απο το θ.Fermat θα ίσχυε :
f'(xo) = 0 , το οποίο είναι άτοπο καθώς μόλις πριν δείξαμε οτι είναι f'(χ) > 0 , για κάθε χ > α .
*Αυτό μπορεί να δειχθεί εύκολα . Εαν η f ήταν κυρτή στο (0,α) και είχε μέγιστο στο x = b Ε (0,α) , τότε θα ίσχυε για κάθε χ Ε (0,α):
f(x) >= f(b) + f'(b)(x - b) = f(b) => λόγω Θ.Fermat
f(x) >= f(b)
Το οποίο είναι άτοπο καθώς το f(b) είναι το μέγιστο , οπότε θα έπρεπε f(x) <= f(b) . Άρα η f είναι κοίλη στο (0,α).
Εν τέλει λοιπόν το b E (0,α) είναι το μέγιστο της f .
Cade
Πολύ δραστήριο μέλος
Ο Cade αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Απόφοιτος λυκείου. Έχει γράψει 851 μηνύματα.

28-09-23

13:59
Γραφω μια πιο σύντομη.
Ορίζω g(x)=f(-lnx), 0<x≤1, g(0)=0. Η g είναι συνεχής και επειδή g(0)=0=g(1), g>0 παίρνει μέγιστη τιμή σε κάποιο κε(0,1). Οπότε η f παίρνει μέγιστη τιμή στο b=-lnκ. Τώρα αρκεί να δείξουμε ότι bε(0,α). Έστω b≥α, τότε στο [b, +00) έχουμε τις εξής περιπτώσεις:
1) f' γν. αύξουσα. Για x>b=>f'(x)>0 άτοπο λόγω του δοσμένου ορίου.
2) f' γν φθίνουσα. Θα υπάρχει ξ με f'(ξ)<0 και για x>ξ : f(x)≤f(ξ)+f'(ξ)(x-ξ), που πάλι ειναι άτοπο αν πάρουμε όριο. Άρα bε(0,α).
Ορίζω g(x)=f(-lnx), 0<x≤1, g(0)=0. Η g είναι συνεχής και επειδή g(0)=0=g(1), g>0 παίρνει μέγιστη τιμή σε κάποιο κε(0,1). Οπότε η f παίρνει μέγιστη τιμή στο b=-lnκ. Τώρα αρκεί να δείξουμε ότι bε(0,α). Έστω b≥α, τότε στο [b, +00) έχουμε τις εξής περιπτώσεις:
1) f' γν. αύξουσα. Για x>b=>f'(x)>0 άτοπο λόγω του δοσμένου ορίου.
2) f' γν φθίνουσα. Θα υπάρχει ξ με f'(ξ)<0 και για x>ξ : f(x)≤f(ξ)+f'(ξ)(x-ξ), που πάλι ειναι άτοπο αν πάρουμε όριο. Άρα bε(0,α).
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3,928 μηνύματα.

28-09-23

19:01
Δεν εχω κατσει να ασχοληθω να τη λυσω παντως μου φαινεται οτι εχεις κανει ενα λαθακι.Λες στο διαστημα [0,α] η f λογω συνεχειας θα χει μια μεγιστη και μια ελαχιστη τιμη λογω του γνωστου θεωρηματος.Δεκτο.Λες μετα εστω οτι το μεγιστο το εχει στο α.Μιλας ομως σε εκεινο το διαστημα αυστηρα!Οποτε αφου το α δεν ειναι εσωτερικο του διαστηματος αυτου δεν μπορεις να κανεις φερματ και να πεις f'(a)=0.Εσυ λες μετα προκειμενου να το εφαρμοσεις πονηρα σκεπτομενος εσωτερικο το α του [0,+00).Ομως δεν σημαινει οτι αφου το α ειναι μεγιστο στο διαστημα [0,α] θα ειναι και τοπικο ακροτατο στο [0,+00).Δες τον ορισμο του τοπικου ακροτατου.Θες δ>0 τετοιο ωστε f(x)<=f(x0) για χ στην τομη του πεδιου ορισμου με το (χ0-δ,χ0+δ).Aρα εσυ πως ξερεις οτι στη δεξια γειτονια του χ0 αυτο το δ λειτουργει??Αρα θεωρω οτι δεν λυνεται ετσι η ασκηση.Θα πρότεινα την εξής λύση :
Η f είναι συνεχής στο [0,α] , οπότε απο το ΘΜΕΤ θα παίρνει μια ελάχιστη και μια μέγιστη τιμή σε αυτό το διάστημα . Ξέρουμε οτι f(x) > 0 για κάθε χ > 0 και οτι f(0) = 0 . Οπότε το 0 είναι σημείο ελαχίστου .
Ας υποθέσουμε οτι το χ = α είναι το σημείο μεγίστου . Σε αυτή την περίπτωση επειδή η f είναι παραγωγίσιμη , και παρουσιάζει ακρότατο στο α , το οποίο είναι εσωτερικό σημείο του πεδίου ορισμού , θα ισχύει απο το Θ.Fermat :
f'(α) = 0
Το α όμως είναι το μοναδικό σημείο καμπής . Οπότε αυτό σημαίνει οτι η f αλλάζει κυρτότητα εκατέρωθεν του α.
Απο το ΘΜΤ για την f στο [0,α] θα υπάρχει ξ Ε (0,α) :
f'(ξ) = f(α)/α , το οποίο είναι θετικό καθώς α > 0 και f(x) > 0 για κάθε χ > 0 .
Έτσι έχουμε ξ < α , με f'(ξ) > f'(α) = 0
Δηλαδή η f' είναι γνησίως φθίνουσα στο [0,α] και γνησίως αύξουσα για χ > α .
Απο το ΘΜΤ όμως για την f στο [α,χ] , υπάρχει ζ Ε (α,χ) :
f'(ζ) = [ f(χ) - f(α) ]/(χ - α)
Εφόσον ζ > α θα πρέπει να ισχύει το εξής εφόσον η f' είναι γνησίως αύξουσα για χ > α :
f'(ζ) > f'(α) = 0 =>
[ f(χ) - f(α) ]/(χ - α) > 0 =>
lim { [ f(χ) - f(α) ]/(χ - α) } > 0 =>
x->+oo
0 > 0
Άτοπο.
Άρα το μέγιστο του διαστήματος [0,α] θα παρουσιάζεται σε κάποια θέση b E (0,α) .
Επιπλέον δεν μπορεί να υπάρχει κάποιο μέγιστο για χ > α , διότι εφόσον το α είναι το μοναδικό σημείο καμπής , η f θα είναι είτε κοίλη είτε κυρτή στο (0,α) . Εφόσον το α είναι μέγιστο , η f θα είναι κοίλη στο (0,α) και επομένως κυρτή στο (α,+οο)*.
Δηλαδή η f' είναι γνησίως φθίνουσα στο (0,α] και γνησίως αύξουσα στο [α,+οο) . Οπότε :
x > α =>
f'(x) > f'(α) = 0
Εαν υπήρχε όντως κάποιο μέγιστο στην θέση χο Ε (α,+οο) , τότε απο το θ.Fermat θα ίσχυε :
f'(xo) = 0 , το οποίο είναι άτοπο καθώς μόλις πριν δείξαμε οτι είναι f'(χ) > 0 , για κάθε χ > α .
*Αυτό μπορεί να δειχθεί εύκολα . Εαν η f ήταν κυρτή στο (0,α) και είχε μέγιστο στο x = b Ε (0,α) , τότε θα ίσχυε για κάθε χ Ε (0,α):
f(x) >= f(b) + f'(b)(x - b) = f(b) => λόγω Θ.Fermat
f(x) >= f(b)
Το οποίο είναι άτοπο καθώς το f(b) είναι το μέγιστο , οπότε θα έπρεπε f(x) <= f(b) . Άρα η f είναι κοίλη στο (0,α).
Εν τέλει λοιπόν το b E (0,α) είναι το μέγιστο της f .
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11,295 μηνύματα.

28-09-23

19:27
Δεν εχω κατσει να ασχοληθω να τη λυσω παντως μου φαινεται οτι εχεις κανει ενα λαθακι.Λες στο διαστημα [0,α] η f λογω συνεχειας θα χει μια μεγιστη και μια ελαχιστη τιμη λογω του γνωστου θεωρηματος.Δεκτο.Λες μετα εστω οτι το μεγιστο το εχει στο α.Μιλας ομως σε εκεινο το διαστημα αυστηρα!Οποτε αφου το α δεν ειναι εσωτερικο του διαστηματος αυτου δεν μπορεις να κανεις φερματ και να πεις f'(a)=0.
Δεν παίζει ρόλο το γεγονός οτι το α δεν είναι εσωτερικό σημείο του [0,α]. Εξακολουθεί να είναι εσωτερικό σημείο του πεδίου ορισμού οπότε το θεώρημα Fermat θα πρέπει να ισχύει κανονικά . Στην ουσία ισχυρίζομαι οτι το μέγιστο στο διάστημα αυτό θα είναι επιπλέον και το μέγιστο της f γενικά ( άρα θα είναι ακρότατο της f ).Εσυ λες μετα προκειμενου να το εφαρμοσεις πονηρα σκεπτομενος εσωτερικο το α του [0,+00).Ομως δεν σημαινει οτι αφου το α ειναι μεγιστο στο διαστημα [0,α] θα ειναι και τοπικο ακροτατο στο [0,+00).
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 9 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 258 μέλη διάβασαν αυτό το θέμα:
- eirinipap
- Debugging_Demon
- exotic xo
- Giorgosvr
- Qwerty 0
- iiTzArismaltor_
- Than003
- Hased Babis
- Kate1914
- bibliofagos
- Corfu kitty
- panosT436
- jellojina
- georgetherrr
- angela_k
- Jomo
- Joji
- Hecticism
- pnf292
- kost28
- suaimhneas
- Unboxholics
- Greg25
- BatGuin
- redpointer
- Albert.123
- Leo komm
- P.Dam.
- Steliosgkougkou
- chjan
- Evangeloz
- jYanniss
- love_to_learn
- wmaria
- Maynard
- χημεια4λαιφ
- Reader
- donut_daddy
- marikakitsou16
- Scandal
- physicscrazy
- Lia 2006
- Wonderkid
- chester20080
- panaman
- Msp1
- Sotis
- mirara
- melver
- grad778
- nickd
- Chrisphys
- V@Per
- sakplat
- ssalex
- despoina13
- catlover033
- carnage
- Μιχαήλ
- eukleidhs1821
- vas2017
- beatrixx
- phleidhs
- gegeorgiou90
- Drglitterstar
- agg41
- thepigod762
- Helen06
- Primary Care
- math2arch
- MrDragonboy
- chrismpd
- Μήτσος10
- bill09876
- Paragontas7000
- ikigai
- Marel
- soleilst
- Startx0
- marilenaaa
- EllieKal
- gzois
- akis_95
- EFAKIT
- Φινεύς
- tsiobieman
- estrela
- Lifelong Learner
- Annie
- Panatha mono
- Mitsaras23
- Isa
- ggl
- BiteTheDust
- Chris180
- aplalew
- user111
- Chemwizard
- giannhs2001
- Mukumbura
- MR WHITE
- SIAmia
- supertom4000
- J.Cameron
- ougkampougka
- persour
- Totreno
- sotirislk
- Specon
- Mariosm.
- Claire05
- Giorgos216
- Jimpower
- shezza94
- kwstasloul
- kan3nas
- dmav
- Obi-Wan Kenobi
- Nancysmilkyway
- Νομάρχης
- ogigidi
- ένας τυχαίος
- Hmmytheos
- constansn
- cannot_log_in
- hello1234
- ilal1200
- Alessandra Eliza
- Giannis327
- phoni
- aggorf
- Nala
- Frozensun
- xrisamikol
- Ilovemycats27
- PanosApo
- nik64
- angies
- dimitris_eee
- mike19
- angeloskar
- eltqt
- CrusaderKingsIII
- flaura
- elevag
- Patroklos
- Anonymous1
- IcedBreaje
- kiyoshi
- nicole1982
- Lost_In_Life
- Γατέχων
- AggelikiGr
- Nansytsg
- Athens2002
- k4t
- Maria_Xagorari
- suuuuiiii
- SoyN
- thecrazycretan
- Jesse_
- A350
- antonis97
- Ιωάννης1234
- george777
- Abiogenesis
- Enhypen
- Mary06
- arko
- Giorgkalo
- velentzakoss
- Giota_pel
- AnnaRd
- Νικολινα
- NikNik1995
- BillyTheKid
- Nick_nt
- a namaves
- xristarac
- ilovekpop
- GeorgePap2003
- Sofos Gerontas
- topg
- Γιώτα Γιαννακού
- plantbee
- Peter Pan13
- Ness
- MrDna
- Jojo K
- Mewmaw
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki


