Βοήθεια/Aπορίες στα Μαθηματικά Προσανατολισμού

[Samael]

Ορισμός: Αν

είναι μία συνάρτηση, λέμε ότι η f παρουσιάζει (ολικό) μέγιστο στο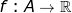

αν για κάθε

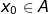ισχύει

Ορισμός: Αν

είναι μία συνάρτηση, λέμε ότι η f παρουσιάζει τοπικό μέγιστο στο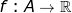

αν υπάρχει ένα

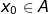τέτοιο ώστε για κάθε

ισχύει

Οι ορισμοί είναι ξεχωριστοί και ο ένας δεν κάνει αναφορά στον άλλον. Απλώς, είναι τετριμμένο να αποδείξεις ότι ένα (ολικό) μέγιστο είναι και τοπικό. Τετριμμένο, μεν, αλλά θέλει απόδειξη (προφανώς εκτός λυκείου αυτά, στο λύκειο θεωρείται προφανές).

Ναι αυτό σκεφτόμουν, οτι παρα είναι τετριμμένο για να ζητηθεί .
Απ'όσο θυμάμαι δεν παίζουν πολύ στο λύκειο με τα δ όμως,ούτε στα όρια .
Έχει αλλάξει κάτι απο τότε ;

 

[Μάρκος Βασίλης]

Ναι αυτό σκεφτόμουν, οτι παρα είναι τετριμμένο για να ζητηθεί .
Απ'όσο θυμάμαι δεν παίζουν πολύ στο λύκειο με τα δ όμως,ούτε στα όρια .
Έχει αλλάξει κάτι απο τότε ;

Όχι, ούτε κατά διάνοια, είναι εκτός φιλοσοφίας. Όλα αυτά καλύπτονται, όταν αυτό χρειάζεται, από τη χρήση του όρου «κοντά».

παρε πχ τη συναρτηση f(x)=(x-1)/e^x εχει τοπικο μεγιστο στο χ=2 το οποιο ομως ειναι και ολικο.εκει τι να αποδειξεις.να παρεις τα ορια στο -00 και στο +00.ψιλοαυτονοητο

Αναφέρομαι στους δύο ορισμούς και στο ότι ο δεύτερος (τοπικό μέγιστο) γενικεύει τον πρώτο, υπό την έννοια ότι ισχύει το εξής:

Αν η f παρουσιάζει στο α ολικό μέγιστο τότε παρουσιάζει και τοπικό μέγιστο εκεί.

Το παραπάνω είναι τετριμμένο, αλλά από τη σκοπιά της λογικής αποτελεί θεώρημα και θέλει απόδειξη. Τίποτα παραπάνω. Σε επίπεδο καθημερινής χρήσης των μαθηματικών δεν μας απασχολεί καθόλου όλο αυτό.

 

[eukleidhs1821]

Δειτε το πιο τρολ θεμα πανελληνιων που επεσε ποτε και αναφερομαι στο δ θεμα του 2008.Τοτε που κλαψανε παρα πολλοι γτ δεν μπορουσαν να δουν το κολπο αυτο!!

 

[Athens2002]

Δειτε το πιο τρολ θεμα πανελληνιων που επεσε ποτε και αναφερομαι στο δ θεμα του 2008.Τοτε που κλαψανε παρα πολλοι γτ δεν μπορουσαν να δουν το κολπο αυτο!!

Τα ερωτήματα β και γ που είναι και στην τωρινή ύλη πλέον νομιζω θεωρούνται πολύ κλασικά

 

[eukleidhs1821]

Τα ερωτήματα β και γ που είναι και στην τωρινή ύλη πλέον νομιζω θεωρούνται πολύ κλασικά

το β οντως ευκολο αλλα μονο 4 μορια το γ ερωτημα δεν το λες και ευκολο για την εποχη του.τοτε ελαχιστοι το λυσανε.ακομα και τωρα θεωρω λιγοι θα το λυνανε.γτ εχει 2 μεταβλητες αρα δυσκολο για επιπεδο λυκειου και + οτι πρεπει να εμφανισεις τα 2 ορια.για το πρωτο ερωτημα μην μιλησουμε καλυτερα το λυσανε ελαχιστοι

Προφανης ερωτηση αλλα πως αποδεινυεται.f(x)>0 αποδειχτε οτι το οριο limf(x)>=0

Αυτόματη ένωση συνεχόμενων μηνυμάτων: 2 Μαΐου 2020

Το βρηκα εστω οτι limf(x)<=0 τοτε κοντα στο χ0 f(x)<=0 ατοπο

Αυτόματη ένωση συνεχόμενων μηνυμάτων: 2 Μαΐου 2020

Kατι αλλο.Αν σας δωσουν 2 συναρτησεις με οριο στο χ0 οτι υπαρχει και μετα σας πουν υπαρχει το οριο του αθροισματος απλα την πατησατε διοτι δεν ξερετε αν το οριο ειναι πραγματικοι αριθμοι γτ αν ειναι απειρα μπορει να πεσετε σε απροσδιοριστια που μπορει να μην υπαρχει το οριο.Παπαγαλιζοντας απο το βιλιο αυτη τη λεπτομερεια δεν την καταλαβαινετε

 

[Μάρκος Βασίλης]

Προφανης ερωτηση αλλα πως αποδεινυεται.f(x)>0 αποδειχτε οτι το οριο limf(x)>=0

Αυτόματη ένωση συνεχόμενων μηνυμάτων: 2 Μαΐου 2020

Το βρηκα εστω οτι limf(x)<=0 τοτε κοντα στο χ0 f(x)<=0 ατοπο

Αυτόματη ένωση συνεχόμενων μηνυμάτων: 2 Μαΐου 2020

Kατι αλλο.Αν σας δωσουν 2 συναρτησεις με οριο στο χ0 οτι υπαρχει και μετα σας πουν υπαρχει το οριο του αθροισματος απλα την πατησατε διοτι δεν ξερετε αν το οριο ειναι πραγματικοι αριθμοι γτ αν ειναι απειρα μπορει να πεσετε σε απροσδιοριστια που μπορει να μην υπαρχει το οριο.Παπαγαλιζοντας απο το βιλιο αυτη τη λεπτομερεια δεν την καταλαβαινετε

Αρχικά, αν ήθελες να το «αποδείξεις» στα πλαίσια της σχολικής ύλης με απαγωγή σε άτοπο θα έπρεπε να υποθέσεις ότι

και όχι «μικρότερο ή ίσο». Αλλά, όπως και να έχει, δεν είναι στο πνεύμα του σχολικού βιβλίου τέτοιου είδους ερωτήσεις, οπότε δε θα ζητούσαμε κάτι τέτοιο.

Σε σχέση με το άλλο, γενικά στον απειροστικό όταν λέμε ότι ένα όριο υπάρχει εννοούμε ότι είναι πραγματικός αριθμός. Αν θέλουμε να συμπεριλάβουμε και τα άπειρα στην όλη υπόθεση χρησιμοποιούμε εκφράσεις του τύπου το όριο υπάρχει και είναι πραγματικός αριθμός ή άπειρο ή το όριο υπάρχει και είναι πραγματικός αριθμός για να αποκλείσουμε όποια παρανόηση. Δεν είναι ο στόχος των θεμάτων απλά να παίξουν με τις λέξεις - γι' αυτό και τέτοια θέματα δεν είναι «έξυπνα» αλλά αστοχίες της όποιας εξεταστικής επιτροπής.

 

[eukleidhs1821]

Αρχικά, αν ήθελες να το «αποδείξεις» στα πλαίσια της σχολικής ύλης με απαγωγή σε άτοπο θα έπρεπε να υποθέσεις ότι

και όχι «μικρότερο ή ίσο». Αλλά, όπως και να έχει, δεν είναι στο πνεύμα του σχολικού βιβλίου τέτοιου είδους ερωτήσεις, οπότε δε θα ζητούσαμε κάτι τέτοιο.

Σε σχέση με το άλλο, γενικά στον απειροστικό όταν λέμε ότι ένα όριο υπάρχει εννοούμε ότι είναι πραγματικός αριθμός. Αν θέλουμε να συμπεριλάβουμε και τα άπειρα στην όλη υπόθεση χρησιμοποιούμε εκφράσεις του τύπου το όριο υπάρχει και είναι πραγματικός αριθμός ή άπειρο ή το όριο υπάρχει και είναι πραγματικός αριθμός για να αποκλείσουμε όποια παρανόηση. Δεν είναι ο στόχος των θεμάτων απλά να παίξουν με τις λέξεις - γι' αυτό και τέτοια θέματα δεν είναι «έξυπνα» αλλά αστοχίες της όποιας εξεταστικής επιτροπής.

ωπα εβαλα και ισον κατα λαθος στην υποθεση.οκ λαθος μου.αν σου πει υπαρχει χωρις να σου πει τι ειναι τοτε δεν μπορεις να πεις οτι ειναι πραγματικος αριθμος.

Αυτόματη ένωση συνεχόμενων μηνυμάτων: 2 Μαΐου 2020

Aκουστε θεμα που θα ναι σωστο λαθος με αιτιολογηση σουπερ σοσαρα.Αν δεν υπαρχουν τα ορια 2 συναρτησεων δεν υπαρχει το οριο του αθροισματος.Λαθος με αντιπαραδειγμα τις 1/χ και -1/χ.

 

[Papachrist]

Καλησπέρα θα μπορούσατε να μου στείλετε τις λύσεις λύσεις των θεμάτων α και γ....αν γίνεται σήμερα γιατί έχω νυκτερινό πρόγραμμα ίντερνετ από 8 το βράδυ μέχρι 12 αύριο το μεσημέρι

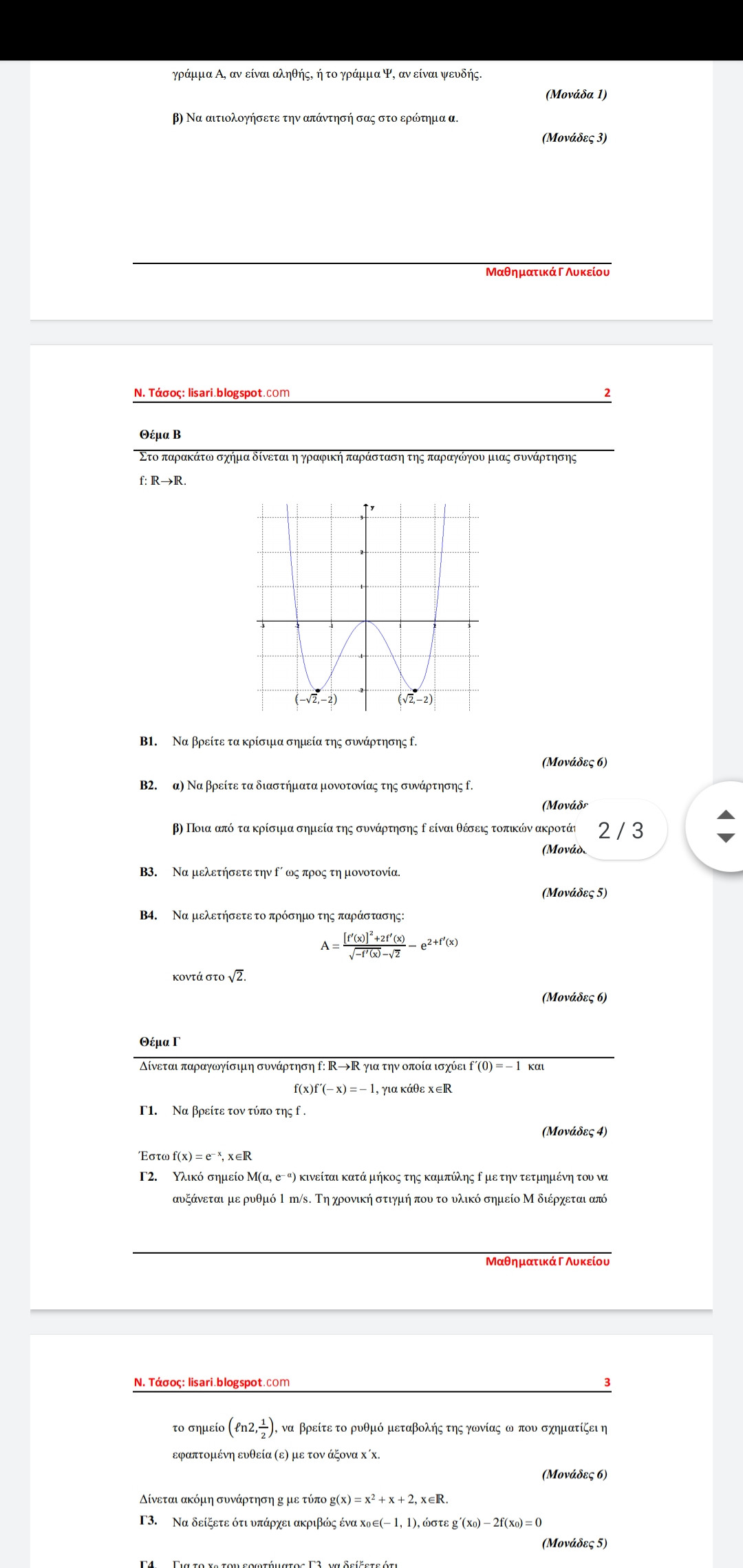
...επομένως παρακαλώ αν γίνεται σήμερα γιατί δεν θα μπορώ να τα μελετήσω αλλιώς... ευχαριστώ εκ των προτέρων(αν γίνεται χειρόγραφα παρακαλώ)

 

[eukleidhs1821]

κατα τα αλλα λεγατε πιο πανω δεν μπορει να πεσει η a^x.

 

[Panagiotis849]

Καλησπέρα θα μπορούσατε να μου στείλετε τις λύσεις λύσεις των θεμάτων α και γ....αν γίνεται σήμερα γιατί έχω νυκτερινό πρόγραμμα ίντερνετ από 8 το βράδυ μέχρι 12 αύριο το μεσημέριView attachment 69401View attachment 69402View attachment 69403...επομένως παρακαλώ αν γίνεται σήμερα γιατί δεν θα μπορώ να τα μελετήσω αλλιώς... ευχαριστώ εκ των προτέρων(αν γίνεται χειρόγραφα παρακαλώ)

Χλωμό μου φαίνεται να βρεις κάποιον τέτοια ώρα να στα στείλει

 

[Papachrist]

Χλωμό μου φαίνεται να βρεις κάποιον τέτοια ώρα να στα στείλει

Έστω αύριο το πρωί ...μπορείς εσύ αν γίνεται το θέμα δ

 

[eukleidhs1821]

To πολλαπλης ειναι καλη ερωτηση που ειναι αρκετα δυσκολη.Απαντιεται με αντιπαραδειγμα.εστω η συναρτηση με διπλο τυπο f(x)=x^2+1 x>=0 ,f(x)=x^2-1,x<0 limαπολυτοφ οταν χ τεινει στο μηδεν=1 ομως το οριο της f οταν χ τεινει στο ο απο δεξια ειναι 1 απο αριστερα ειναι -1.Οπότε καλλιστα μπορει να μην υπαρχει καν το οριο

Αυτόματη ένωση συνεχόμενων μηνυμάτων: 3 Μαΐου 2020

G1.βαζεις οπου χ το -χ και εχεις φ(-χ)φ'(χ)=-1 (1) εξισωνεις τα πρωτα μελη αφου τα δευτερα ειναι ισα και εχεις φ(-χ)φ'(χ)=φ(χ)φ'(-χ) δημιουργειται μια παραγωγος
(φ(-χ)φ(χ))'=0 αρα φ(-χ)φ(χ)=c φ(0)=1 αρα φ(χ)φ(-χ)=1 (2) διαιρεις κατα μελη τις (1) και (2) και εχεις φ'(χ)/φ(χ)=-1 το πρωτο μελος ειναι γνωστη παραγωγος (lnφ(χ))'=(-χ)' οποτε lnφ(χ)=-χ+c1 lnφ(0)=c1 c1=0 αρα lnφ(χ)=-χ φ(χ)=e^-x

Να αιτιολογηθει οτι φ(χ) διαφορο του μηδενος απο την μορφη της συναρτησιακης και λογω συνεχειας διατηρει σταθερο προσημο φ(0)=1 αρα φ(χ)>0 για καθε χ στο R.Eτσι μπορουμε να διαρεσουμε κατα μελη και να βγαλουμε το απολυτο στον ln

Αυτόματη ένωση συνεχόμενων μηνυμάτων: 3 Μαΐου 2020

G2.H κλιση της εφαπτομενης οπως γνωριζουμε ειναι tanω(t)=-e^-(x(t)) x'(t) χ'(t)=1 οποτε tanω(t)=-e^(-x(t))
Παραγωγιζουμε και εχουμε 1/cos^2ω(t)ω'(t)=e^-(x(t)) x'(t) καταληγουμε 1/cos^2ω(t)ω'(t)=e^-(x(t)) την χρονικη στιγμη που θελουμε ειναι tanω(t)=-1/2 οποτε 1/cos^2ω(t)=1+tan^2ω(t)=1+1/4=5/4 αρα 5/4 ω'(t0)=1/2 ω'(t0)=2/5

Αυτόματη ένωση συνεχόμενων μηνυμάτων: 3 Μαΐου 2020

Aν μπορει ο samuel να τα γραψει με καλυτερο τροπο γτ εγω δεν ξερω πως να φαινονται καλυτερα αν θελει

 

[Samael]

To πολλαπλης ειναι καλη ερωτηση που ειναι αρκετα δυσκολη.Απαντιεται με αντιπαραδειγμα.εστω η συναρτηση με διπλο τυπο f(x)=x^2+1 x>=0 ,f(x)=x^2-1,x<0 limαπολυτοφ οταν χ τεινει στο μηδεν=1 ομως το οριο της f οταν χ τεινει στο ο απο δεξια ειναι 1 απο αριστερα ειναι -1.Οπότε καλλιστα μπορει να μην υπαρχει καν το οριο

Αυτόματη ένωση συνεχόμενων μηνυμάτων: 3 Μαΐου 2020

G1.βαζεις οπου χ το -χ και εχεις φ(-χ)φ'(χ)=-1 (1) εξισωνεις τα πρωτα μελη αφου τα δευτερα ειναι ισα και εχεις φ(-χ)φ'(χ)=φ(χ)φ'(-χ) δημιουργειται μια παραγωγος
(φ(-χ)φ(χ))'=0 αρα φ(-χ)φ(χ)=c φ(0)=1 αρα φ(χ)φ(-χ)=1 (2) διαιρεις κατα μελη τις (1) και (2) και εχεις φ'(χ)/φ(χ)=-1 το πρωτο μελος ειναι γνωστη παραγωγος (lnφ(χ))'=(-χ)' οποτε lnφ(χ)=-χ+c1 lnφ(0)=c1 c1=0 αρα lnφ(χ)=-χ φ(χ)=e^-x

Η παρατήρηση είναι σωστή και το ξεκίνησες καλά,ωστόσο δεν φαίνεται ξεκάθαρα απο το ενδιάμεσο πόρισμα το ζητούμενο .

Αρκεί να θεωρήσει κάποιος μια συνάρτηση που το όριο της στο xo υπάρχει και ισχύει :

lim|f(x)|=|l| =>
lim|f(x)| = |limf(x)| =>
|limf(x)| = |l|

Θεωρώ :
limf(x) = y

Οπότε |y| = |l| => y = l ή y = -l

Η πρόταση ήταν :
Αν lim|f(x)| = |l| =/> y = l ή y=-l

Εμείς δείξαμε οτι ο ισχυρισμός είναι σίγουρα λανθασμένος εαν η f(x) έχει όριο στο xo, οπότε αυτό μας φτάνει για να αποφανθούμε οτι η πρόταση είναι ψευδής .

 

[eukleidhs1821]

G3.g'(x)=2x+1 θεωρουμε τη συναρτηση h(x)=2x+1-2e^-x Βολζανο στο [-1,1] και μετα δειχνουμε τη μοναδικοτητα μεσω μονοτονιας.

Αυτόματη ένωση συνεχόμενων μηνυμάτων: 3 Μαΐου 2020

Η παρατήρηση είναι σωστή και το ξεκίνησες καλά,ωστόσο δεν φαίνεται ξεκάθαρα απο το ενδιάμεσο πόρισμα το ζητούμενο .

Αρκεί να θεωρήσει κάποιος μια συνάρτηση που το όριο της στο xo υπάρχει και ισχύει :

lim|f(x)|=|l| =>
lim|f(x)| = |limf(x)| =>
|limf(x)| = |l|

Θεωρώ :
limf(x) = y

Οπότε |y| = |l| => y = l ή y = -l

Η πρόταση ήταν :
Αν lim|f(x)| = |l| =/> y = l ή y=-l

Εμείς δείξαμε οτι ο ισχυρισμός είναι σίγουρα λανθασμένος εαν η f(x) έχει όριο στο xo, οπότε αυτό μας φτάνει για να αποφανθούμε οτι η πρόταση είναι ψευδής .

μα το οριο μπορει να μην υπαρχει καν φιλε μου και δεν σου λεει οτι υπαρχει το οριο.οποτε εγω εβγαλα αντιπαραδειγμα που δειχνω οτι δεν υπαρχει το οριο ενω υπαρχει το οριο της απολυτου

Αυτόματη ένωση συνεχόμενων μηνυμάτων: 3 Μαΐου 2020

Μισο λεπτο.Η προταση λεει δεν συνεπαγεται οτι το οριο ειναι αυτο.Εσυ βγαζεις οτι συνεπαγεται.Για να ισχυριστεις αυτο επρεπε να σου λεει οτι το οριο υπαρχει.Αν το οριο υπηρχε οντως εχεις δικιο ομως η προταση δεν το διευκρινιζει οποτε ειναι σωστος ο ισχυρισμος της προτασης.

Αυτόματη ένωση συνεχόμενων μηνυμάτων: 3 Μαΐου 2020

Για να ισχυει αυτο που λεει ο samuel επρεπε η συναρτηση να ειχε το ιδιο προσημο γυρω απο το χ0.Αν ομως η συναρτηση αλλαζει προσημο γυρω απο το χ0 οπως στο αντιπαραδειγμα που εκανα το οριο δεν υπαρχει καν.

 

[Samael]

G3.g'(x)=2x+1 θεωρουμε τη συναρτηση h(x)=2x+1-2e^-x Βολζανο στο [-1,1] και μετα δειχνουμε τη μοναδικοτητα μεσω μονοτονιας.

Αυτόματη ένωση συνεχόμενων μηνυμάτων: 3 Μαΐου 2020

μα το οριο μπορει να μην υπαρχει καν φιλε μου και δεν σου λεει οτι υπαρχει το οριο.οποτε εγω εβγαλα αντιπαραδειγμα που δειχνω οτι δεν υπαρχει το οριο ενω υπαρχει το οριο της απολυτου

Δεν είπα οτι είσαι *λάθος* ,εννοούσα απλά οτι πρέπει να το κάνεις λίγο πιο ξεκάθαρο

 

[eukleidhs1821]

Δεν είπα οτι είσαι *λάθος* ,εννοούσα απλά οτι πρέπει να το κάνεις λίγο πιο ξεκάθαρο

εσυ λες οτι η προταση ειναι λαθος.εγω λεω ειναι σωστη.το απεδειξα με αντιπαραδειγμα οτι μπορει να μην υπαρχει καν το οριο.

 

[Samael]

εσυ λες οτι η προταση ειναι λαθος.εγω λεω ειναι σωστη.το απεδειξα με αντιπαραδειγμα οτι μπορει να μην υπαρχει καν το οριο.

Ο ίδιος το λες,εαν το όριο δεν υπάρχει πως γίνεται ο ισχυρισμός να είναι αληθής ;
Αφού δεν μπορείς να κάνεις καν λόγο για την τιμή αλήθειας της δεξιάς πρότασης εφόσον το
lim f(x) που είναι δεξιά δεν ορίζεται . Άρα δεν έχει καν νόημα να αναρωτηθείς για μια τέτοια πρόταση εαν είναι αληθής ή ψευδής .

Επομένως δέχεσαι οτι το όριο υπάρχει και μέσω των παραπάνω βημάτων που έγραψα οδηγείσαι στο οτι η πρόταση είναι ψευδής .

Κατά την γνώμη μου είναι μια πολύ δύσκολη ερώτηση γιατί απαιτεί κάποιος να χρησιμοποιεί λογική σε λίγο πιο προχωρημένο επίπεδο απ'ότι συνήθως διδάσκεται(ή μάλλον δεν διδάσκεται) . Εαν και είμαι αρκετά σίγουρος οτι έτσι είναι, η γνώμη του @Μάρκος Βασίλης είναι πάντα χρήσιμη .

 

[eukleidhs1821]

G4.Πονηροτατη ασκηση που λυνεται χωρις γνωσεις αναλυσης.H G(X) ως τριωνυμο επειδη α>0 εχει ελαχιστη τιμη την -Δ/4α=7/4 g(x)>=7/4 2f(x)=2e^-x>0 αρα g(x)+2f(x)>7/4 Θα αποδειξουμε οτι χ0^2+3χ0+3<=7/4 (1) Θεωρουμε το τριωνυμο h(x)=x^2+3x+3-7/4 βλεπουμε αν κανουμε τα γνωστα οτι για το χ0 του γ ερωτηματος που ανηκει στο (-1,1) ισχυει η σχεση (1).Αρα απο μεταβατικη ιδιοτητα βγαλαμε το ζητουμενο

Αυτόματη ένωση συνεχόμενων μηνυμάτων: 3 Μαΐου 2020

Ο ίδιος το λες,εαν το όριο δεν υπάρχει πως γίνεται ο ισχυρισμός να είναι αληθής ;
Αφού δεν μπορείς να κάνεις καν λόγο για την τιμή αλήθειας της δεξιάς πρότασης εφόσον το
lim f(x) που είναι δεξιά δεν ορίζεται . Άρα δεν έχει καν νόημα να αναρωτηθείς για μια τέτοια πρόταση εαν είναι αληθής ή ψευδής .

Επομένως δέχεσαι οτι το όριο υπάρχει και μέσω των παραπάνω βημάτων που έγραψα οδηγείσαι στο οτι η πρόταση είναι ψευδής .

Κατά την γνώμη μου είναι μια πολύ δύσκολη ερώτηση γιατί απαιτεί κάποιος να χρησιμοποιεί λογική σε λίγο πιο προχωρημένο επίπεδο απ'ότι συνήθως διδάσκεται(ή μάλλον δεν διδάσκεται) . Εαν και είμαι αρκετά σίγουρος οτι έτσι είναι, η γνώμη του @Μάρκος Βασίλης είναι πάντα χρήσιμη .

εσυ απεδειξες οτι αν το οριο υπαρχει μπορεις να ισχυριστεις οτι ειναι +l ή -l.Μα εγω απεδειξα οτι μπορει να μην υπαρχει το οριο.Αρα δεν εχει καν νοημα να πεις με τι ισουται.Δεν δεχτηκα οτι υπαρχει το οριο.Πρεπει να διευκρινιστει αυτο αν και το κολπο εκει ειναι να πιστεψεις οτι το οριο υπαρχει ενω δεν υπαρχει

Αυτόματη ένωση συνεχόμενων μηνυμάτων: 3 Μαΐου 2020

G5.Kαταρχην οριζεται η συνθεση και εχει πεδιο ορισμου το R.Meta βρισκουμε την μονοτονια της g0f αν παρεις τη παραγωγο τη βγαζεις αρνητικη αρα γνησιως φθινουσα.οποτε πρεπει να αποδειξεις τα μεσα οτι ειναι αντιθετη φορα και μετα να το βγαλεις απο τη μονοτονια της συνθεσης

Αυτόματη ένωση συνεχόμενων μηνυμάτων: 3 Μαΐου 2020

Γνωριζουμε δεν ξερω αν πρεπει να το αποδειξεις ή θεωρειται στημενο αυτο ας το πει καποιος που γνωριζει την υλη ΑΠολυτο ημιτονο χ <=απολυτο χ αρα απολυτο χ-απολυτοημιτονο+1/2>=1/2 το τουμπαρω<=2.Αρα λογικα πρεπει να βγαλεις το αλλο >2

Αυτόματη ένωση συνεχόμενων μηνυμάτων: 3 Μαΐου 2020

Της πλακας με μελετη συναρτησης βγαζω e^x-x>=1 πολλαπλασιαζω με 4 4(e^x-x)>=4 αρα απεδειξα τα μεσα κανε μονοτονια της συνθεσης και το απεδειξα.Η ασκηση λυθηκε

 

[Papachrist]

Καλησπέρα θα μπορούσατε να μου στείλετε τις λύσεις του θέματος αυτού καθώς με δυσκολεύει ιδιαίτερα

 

[eukleidhs1821]

Εσεις τις προσπαθειτε καθολου τις ασκησεις ή απλα περιμενετε τις λυσεις να τις αντιγραψετε??Γτ σε 2 μηνες τι θα κανετε?Ελπιζω να τις προσπαθειτε