eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3,928 μηνύματα.

25-04-20

16:06
Eκπληκτικη ασκηση οτι πρεπει για δ θεμα.Μικροτερο ισο και τιμες θεωρημα φερματ!!Θες 2 θεωρηματα φερματ πως ομως.Πας το f(x) στο αλλο μελος και στις 2 ανισωσεις και θεωρεις 2 συναρτησεις.Απο κει και περα πρεπει να αποδειξεις με κριτηριο παρεμβολης οτι το οριο της f στο μηδεν ειναι μηδεν.Αρα οι δυο συναρτησεις εχουν τοπικο ακροτατο στο μηδεν.Δημιουργειται ενα συστημα που υπολογισεις τα φ(π) και φ(π/2).Γυρνας στην πανω σχεση απο τη μια βγαζεις φ(χ)>=ημχ και απο την αλλή βγαζεις φ(χ)<=ημχ+αλλη μια παραταση που αποδεικνυεται θεωρωντας επιπλεον συναρτηση και μελετωντας ως προς μονοτονια οτι ειναι αρνητικο.αρα βγαζεις φ(χ)<=ημχ το οποιο σε συναρτηση με το φ(χ)>=ημχ που εχεις συναληθευει στο φ(χ)=ημχ
kvstas92
Νεοφερμένος
Ο kvstas92 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 22 ετών. Έχει γράψει 18 μηνύματα.

25-04-20

16:11
παναγια μουEκπληκτικη ασκηση οτι πρεπει για δ θεμα.Μικροτερο ισο και τιμες θεωρημα φερματ!!Θες 2 θεωρηματα φερματ πως ομως.Πας το f(x) στο αλλο μελος και στις 2 ανισωσεις και θεωρεις 2 συναρτησεις.Απο κει και περα πρεπει να αποδειξεις με κριτηριο παρεμβολης οτι το οριο της f στο μηδεν ειναι μηδεν.Αρα οι δυο συναρτησεις εχουν τοπικο ακροτατο στο μηδεν.Δημιουργειται ενα συστημα που υπολογισεις τα φ(π) και φ(π/2).Γυρνας στην πανω σχεση απο τη μια βγαζεις φ(χ)>=ημχ και απο την αλλή βγαζεις φ(χ)<=ημχ+αλλη μια παραταση που αποδεικνυεται θεωρωντας επιπλεον συναρτηση και μελετωντας ως προς μονοτονια οτι ειναι αρνητικο.αρα βγαζεις φ(χ)<=ημχ το οποιο σε συναρτηση με το φ(χ)>=ημχ που εχεις συναληθευει στο φ(χ)=ημχ
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3,928 μηνύματα.

25-04-20

16:27
μισο λεπτο κατι δεν λεω σωστα καταληγω φ(χ)>=ημχ και φ(χ)<=ημχ+(e^x-1-6x)/5 -φ(χ)>=-ημχ-(e^x-1-6x)/5 προσθετω κατα μελη 0>=-(e^x-1-6x)/5 e^x-1-6x>>=0παναγια μου
Αυτόματη ένωση συνεχόμενων μηνυμάτων:
μαρκο βασιλη κατι κανω λαθος στο τελος
Αυτόματη ένωση συνεχόμενων μηνυμάτων:
θα μπορουσες να δημιουργησεις και το οριο της παραγωγου και να κανεις απευθειας κριτηριο παρεμβολης αλλα δε συμπιπτουν τα ακριανα ορια οποτε δεν μπορεις να το εφαρμοσεις.για καποιο περιεργο λογο δεν μπορω να βγαλω το φ(χ)<=ημχ και σε συναρτηση με το φ(χ)>=ημχ να τα βγαλω ισα
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3,928 μηνύματα.

25-04-20

17:45
μαρκο βασιλη απαντα ρε φιλε
Μάρκος Βασίλης
Πολύ δραστήριο μέλος
Ο Βασίλης αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 28 ετών, Διδακτορικός και μας γράφει από Καισαριανή (Αττική). Έχει γράψει 1,871 μηνύματα.

25-04-20

19:03
Η σχέση είναι αυτή, αν την είδα καλά:

Αντικαθιστώντας το 0 - κλασικό αυτό σε τέτοιες ασκήσεις - παίρνουμε αμέσως ότι f(0)=0.
Θεωρούμε για αρχή τη συνάρτηση:

οπότε αρκεί να δείξουμε ότι η g είναι μηδενική. Αρχικά, ας παρατηρήσουμε ότι g(0)=0 και:

Επίσης, g'(0)=0 (εύκολο αυτό, απλά παραγωγίζουμε).
Οπότε η δοσμένη σχέση ξαναγράφεται ως εξής:

Πού, άμα κάνουμε τις πράξεις, δίνει:
 (1)
(1)
Τώρα, αν x>0, διαιρώντας με x παίρνουμε:

οπότε, παίρνοντας και ένα όριο καθώς το χ «πέφτει» προς το 0 έχουμε:

αφού:

Αν τώρα x<0 τότε διαιρούμε και πάλι με x, απλώς θα αλλάξει η φορά, οπότε παίρνουμε:

και, για τους ίδιους λόγους παίρνοντας όριο καθώς το x «ανεβαίνει» προς το 0:

Οπότε παίρνομε τις σχέσεις:

Λύνουμε το σύστημα και βρίσκουμε:

Οπότε, αντικαθιστώντας στην (1) παίρνουμε:

που ήταν και το ζητούμενο.
Μερικές οδηγίες για αυτές τις ασκήσεις είναι:

Αντικαθιστώντας το 0 - κλασικό αυτό σε τέτοιες ασκήσεις - παίρνουμε αμέσως ότι f(0)=0.
Θεωρούμε για αρχή τη συνάρτηση:

οπότε αρκεί να δείξουμε ότι η g είναι μηδενική. Αρχικά, ας παρατηρήσουμε ότι g(0)=0 και:

Επίσης, g'(0)=0 (εύκολο αυτό, απλά παραγωγίζουμε).
Οπότε η δοσμένη σχέση ξαναγράφεται ως εξής:

Πού, άμα κάνουμε τις πράξεις, δίνει:

Τώρα, αν x>0, διαιρώντας με x παίρνουμε:

οπότε, παίρνοντας και ένα όριο καθώς το χ «πέφτει» προς το 0 έχουμε:

αφού:

Αν τώρα x<0 τότε διαιρούμε και πάλι με x, απλώς θα αλλάξει η φορά, οπότε παίρνουμε:

και, για τους ίδιους λόγους παίρνοντας όριο καθώς το x «ανεβαίνει» προς το 0:

Οπότε παίρνομε τις σχέσεις:

Λύνουμε το σύστημα και βρίσκουμε:

Οπότε, αντικαθιστώντας στην (1) παίρνουμε:

που ήταν και το ζητούμενο.
Μερικές οδηγίες για αυτές τις ασκήσεις είναι:
- Δεν πανικοβαλόμαστε.
- Όταν σου δίνει και κάποιες τιμές της συνάρτησης, δοκίμασε να τις αξιοποιήσεις κάπως. Αν είναι τιμές της ίδιας της συνάρτησης, αντικατάστησε τα νούμερα να δεις τι βγάζει. Αν είναι, όπως εδώ, για κάποια παράγωγο, τότε δες την επόμενη συμβουλή (χεχεχε).
- Σου λέει κάτι για την παράγωγο και σου δίνει και μία ανισότητα. Σιγά τα αυγά, αφού δεν έχει νόημα να παραγωγίσουμε μία ανισότητα. Οπότε, εδώ έρχεται λίγο μία πιο ουσιαστική σκέψη στο παιχνίδι. Τι είναι η παράγωγος; Μα, το όριο του λόγου μεταβολής. Όριο, λοιπόν, σου δίνει σαν υπόθεση. Και σου δίνει και ανισότητα. Χμμμ... Μπορείς να πάρεις όριο σε ανισότητα χωρίς να «χαλάσει». Άρα, κάπως πρέπει να εμφανίσεις τον λόγο μεταβολής μέσα στην ανισότητα.
- Εδώ κάναμε και ένα άλλο κόλπο. Σου έλεγε, δείξε ότι f(x)=ημx. Ωραία, αλλά αυτό δε σημαίνει ότι δεν μπορείς να παίξεις με το ζητούμενο. Σύνηθες τρυκ είναι αυτό που είδες, μιας και το να δείξεις ότι μία συνάρτηση είναι 0 είναι, συνήθως, λίγο πιο απλό στο μάτι.
- Γενικά, σχεδόν ποτέ μία δύσκολη άσκηση δε βγαίνει με το να ξεκινήσουμε από τα δεδομένα μας και, ντουγρού, να πάμε στα ζητούμενα με συμπεράσματα που θα βγάζουμε το ένα πίσω από το άλλο (forward chaining, που λέμε). Το σύνηθες εδώ είναι να δουλεύουμε με τη μέθοδο του «αρκεί». Ξεκινάς από το ζητούμενο και βρίσκεις είτε άλλες διατυπώσεις του (όπως κάναμε εδώ) είτε πράγματα που αν ισχύουν, δίνουν μαζί με άλλα συμπεράσματα ενδεχομένως, και το ζητούμενο.
- Keep it simple! Μαθηματικά κάνουμε, δεν κάνουμε πυρηνική φυσική (αυτό πάει και σε άλλο thread... :Ρ). Τι κάναμε παραπάνω στην ουσία; Είδαμε στις υποθέσεις μία παράγωγο σε ένα σημείο, πήραμε τον ορισμό της παραγώγου. Είδαμε το
σε ένα άλλο σημείο, το διαιρέσαμε με x και πήραμε ορισμό της παραγώγου. Είδαμε ανισότητα, βρήκαμε κάποια όρια. Απλά πράγματα. Μην πηγαίνει ο νους σου στα περίπλοκα πρώτα - την κάνουν συχνά αυτή τη ζημιά τα φροντιστήρια/ιδιαίτερα, ομολογουμένως. Με τις 4-5 απλές ιδέες θα συνθέσεις το σύνθετο αποτέλεσμα στο τέλος.

eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3,928 μηνύματα.

25-04-20

19:33
βγαινει και με 2 φερματ φιλεΗ σχέση είναι αυτή, αν την είδα καλά:

Αντικαθιστώντας το 0 - κλασικό αυτό σε τέτοιες ασκήσεις - παίρνουμε αμέσως ότι f(0)=0.
Θεωρούμε για αρχή τη συνάρτηση:

οπότε αρκεί να δείξουμε ότι η g είναι μηδενική. Αρχικά, ας παρατηρήσουμε ότι g(0)=0 και:

Επίσης, g'(0)=0 (εύκολο αυτό, απλά παραγωγίζουμε).
Οπότε η δοσμένη σχέση ξαναγράφεται ως εξής:

Πού, άμα κάνουμε τις πράξεις, δίνει:
(1)
Τώρα, αν x>0, διαιρώντας με x παίρνουμε:

οπότε, παίρνοντας και ένα όριο καθώς το χ «πέφτει» προς το 0 έχουμε:

αφού:

Αν τώρα x<0 τότε διαιρούμε και πάλι με x, απλώς θα αλλάξει η φορά, οπότε παίρνουμε:

και, για τους ίδιους λόγους παίρνοντας όριο καθώς το x «ανεβαίνει» προς το 0:

Οπότε παίρνομε τις σχέσεις:

Λύνουμε το σύστημα και βρίσκουμε:

Οπότε, αντικαθιστώντας στην (1) παίρνουμε:

που ήταν και το ζητούμενο.
Μερικές οδηγίες για αυτές τις ασκήσεις είναι:
- Δεν πανικοβαλόμαστε.
- Όταν σου δίνει και κάποιες τιμές της συνάρτησης, δοκίμασε να τις αξιοποιήσεις κάπως. Αν είναι τιμές της ίδιας της συνάρτησης, αντικατάστησε τα νούμερα να δεις τι βγάζει. Αν είναι, όπως εδώ, για κάποια παράγωγο, τότε δες την επόμενη συμβουλή (χεχεχε).
- Σου λέει κάτι για την παράγωγο και σου δίνει και μία ανισότητα. Σιγά τα αυγά, αφού δεν έχει νόημα να παραγωγίσουμε μία ανισότητα. Οπότε, εδώ έρχεται λίγο μία πιο ουσιαστική σκέψη στο παιχνίδι. Τι είναι η παράγωγος; Μα, το όριο του λόγου μεταβολής. Όριο, λοιπόν, σου δίνει σαν υπόθεση. Και σου δίνει και ανισότητα. Χμμμ... Μπορείς να πάρεις όριο σε ανισότητα χωρίς να «χαλάσει». Άρα, κάπως πρέπει να εμφανίσεις τον λόγο μεταβολής μέσα στην ανισότητα.
- Εδώ κάναμε και ένα άλλο κόλπο. Σου έλεγε, δείξε ότι f(x)=ημx. Ωραία, αλλά αυτό δε σημαίνει ότι δεν μπορείς να παίξεις με το ζητούμενο. Σύνηθες τρυκ είναι αυτό που είδες, μιας και το να δείξεις ότι μία συνάρτηση είναι 0 είναι, συνήθως, λίγο πιο απλό στο μάτι.
- Γενικά, σχεδόν ποτέ μία δύσκολη άσκηση δε βγαίνει με το να ξεκινήσουμε από τα δεδομένα μας και, ντουγρού, να πάμε στα ζητούμενα με συμπεράσματα που θα βγάζουμε το ένα πίσω από το άλλο (forward chaining, που λέμε). Το σύνηθες εδώ είναι να δουλεύουμε με τη μέθοδο του «αρκεί». Ξεκινάς από το ζητούμενο και βρίσκεις είτε άλλες διατυπώσεις του (όπως κάναμε εδώ) είτε πράγματα που αν ισχύουν, δίνουν μαζί με άλλα συμπεράσματα ενδεχομένως, και το ζητούμενο.
- Keep it simple! Μαθηματικά κάνουμε, δεν κάνουμε πυρηνική φυσική (αυτό πάει και σε άλλο thread... :Ρ). Τι κάναμε παραπάνω στην ουσία; Είδαμε στις υποθέσεις μία παράγωγο σε ένα σημείο, πήραμε τον ορισμό της παραγώγου. Είδαμε το
σε ένα άλλο σημείο, το διαιρέσαμε με x και πήραμε ορισμό της παραγώγου. Είδαμε ανισότητα, βρήκαμε κάποια όρια. Απλά πράγματα. Μην πηγαίνει ο νους σου στα περίπλοκα πρώτα - την κάνουν συχνά αυτή τη ζημιά τα φροντιστήρια/ιδιαίτερα, ομολογουμένως. Με τις 4-5 απλές ιδέες θα συνθέσεις το σύνθετο αποτέλεσμα στο τέλος.
kvstas92
Νεοφερμένος
Ο kvstas92 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 22 ετών. Έχει γράψει 18 μηνύματα.

25-04-20

19:38
εισαι ωραιος, ειχα φτασει κοντα στην λυση σου αλλα ειχα κολλησει σε μια φαση ευχαριστωΗ σχέση είναι αυτή, αν την είδα καλά:

Αντικαθιστώντας το 0 - κλασικό αυτό σε τέτοιες ασκήσεις - παίρνουμε αμέσως ότι f(0)=0.
Θεωρούμε για αρχή τη συνάρτηση:

οπότε αρκεί να δείξουμε ότι η g είναι μηδενική. Αρχικά, ας παρατηρήσουμε ότι g(0)=0 και:

Επίσης, g'(0)=0 (εύκολο αυτό, απλά παραγωγίζουμε).
Οπότε η δοσμένη σχέση ξαναγράφεται ως εξής:

Πού, άμα κάνουμε τις πράξεις, δίνει:
(1)
Τώρα, αν x>0, διαιρώντας με x παίρνουμε:

οπότε, παίρνοντας και ένα όριο καθώς το χ «πέφτει» προς το 0 έχουμε:

αφού:

Αν τώρα x<0 τότε διαιρούμε και πάλι με x, απλώς θα αλλάξει η φορά, οπότε παίρνουμε:

και, για τους ίδιους λόγους παίρνοντας όριο καθώς το x «ανεβαίνει» προς το 0:

Οπότε παίρνομε τις σχέσεις:

Λύνουμε το σύστημα και βρίσκουμε:

Οπότε, αντικαθιστώντας στην (1) παίρνουμε:

που ήταν και το ζητούμενο.
Μερικές οδηγίες για αυτές τις ασκήσεις είναι:
- Δεν πανικοβαλόμαστε.
- Όταν σου δίνει και κάποιες τιμές της συνάρτησης, δοκίμασε να τις αξιοποιήσεις κάπως. Αν είναι τιμές της ίδιας της συνάρτησης, αντικατάστησε τα νούμερα να δεις τι βγάζει. Αν είναι, όπως εδώ, για κάποια παράγωγο, τότε δες την επόμενη συμβουλή (χεχεχε).
- Σου λέει κάτι για την παράγωγο και σου δίνει και μία ανισότητα. Σιγά τα αυγά, αφού δεν έχει νόημα να παραγωγίσουμε μία ανισότητα. Οπότε, εδώ έρχεται λίγο μία πιο ουσιαστική σκέψη στο παιχνίδι. Τι είναι η παράγωγος; Μα, το όριο του λόγου μεταβολής. Όριο, λοιπόν, σου δίνει σαν υπόθεση. Και σου δίνει και ανισότητα. Χμμμ... Μπορείς να πάρεις όριο σε ανισότητα χωρίς να «χαλάσει». Άρα, κάπως πρέπει να εμφανίσεις τον λόγο μεταβολής μέσα στην ανισότητα.
- Εδώ κάναμε και ένα άλλο κόλπο. Σου έλεγε, δείξε ότι f(x)=ημx. Ωραία, αλλά αυτό δε σημαίνει ότι δεν μπορείς να παίξεις με το ζητούμενο. Σύνηθες τρυκ είναι αυτό που είδες, μιας και το να δείξεις ότι μία συνάρτηση είναι 0 είναι, συνήθως, λίγο πιο απλό στο μάτι.
- Γενικά, σχεδόν ποτέ μία δύσκολη άσκηση δε βγαίνει με το να ξεκινήσουμε από τα δεδομένα μας και, ντουγρού, να πάμε στα ζητούμενα με συμπεράσματα που θα βγάζουμε το ένα πίσω από το άλλο (forward chaining, που λέμε). Το σύνηθες εδώ είναι να δουλεύουμε με τη μέθοδο του «αρκεί». Ξεκινάς από το ζητούμενο και βρίσκεις είτε άλλες διατυπώσεις του (όπως κάναμε εδώ) είτε πράγματα που αν ισχύουν, δίνουν μαζί με άλλα συμπεράσματα ενδεχομένως, και το ζητούμενο.
- Keep it simple! Μαθηματικά κάνουμε, δεν κάνουμε πυρηνική φυσική (αυτό πάει και σε άλλο thread... :Ρ). Τι κάναμε παραπάνω στην ουσία; Είδαμε στις υποθέσεις μία παράγωγο σε ένα σημείο, πήραμε τον ορισμό της παραγώγου. Είδαμε το
σε ένα άλλο σημείο, το διαιρέσαμε με x και πήραμε ορισμό της παραγώγου. Είδαμε ανισότητα, βρήκαμε κάποια όρια. Απλά πράγματα. Μην πηγαίνει ο νους σου στα περίπλοκα πρώτα - την κάνουν συχνά αυτή τη ζημιά τα φροντιστήρια/ιδιαίτερα, ομολογουμένως. Με τις 4-5 απλές ιδέες θα συνθέσεις το σύνθετο αποτέλεσμα στο τέλος.
aggelosst9
Εκκολαπτόμενο μέλος
Ο aggelosst9 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Φοιτητής του τμήματος Οικονομικής Επιστήμης Ο.Π.Α. (Αθήνα). Έχει γράψει 125 μηνύματα.

26-04-20

18:17
Είμαι 99% σίγουρος πως στο β χρησιμοποιώ το ξ του Α και κάνω 2 ΘΜΤ αλλά δεν μου βγαίνουν οι πράξεις

eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3,928 μηνύματα.

26-04-20

20:01
τι σπαστικη ασκηση ειναι αυτη.το πρωτο ειναι της πλακας με θμτ στο [1,3] και f'(ξ)=1 στο δευτερο αν κανεις 2 θμτ στο [1,2] και [2,3] δεν σε παει πουθενα.λογικα αξιοποιειες το ξ που απεδειξες με 2 θμτ [1,ξ] [ξ,3] παλι δεν σε παει πουθενα
Tα ξ1,ξ2 ειναι διαφορετικα??Γτ ηλιθιωδως μπορω να πω οτι αν ξ1=ξ2=ξ του πρωτου ερωτηματος βγαζει 2+1=3 αλλα σιγα μην βγαινει ετσι
Αυτόματη ένωση συνεχόμενων μηνυμάτων:
Tα ξ1,ξ2 ειναι διαφορετικα??Γτ ηλιθιωδως μπορω να πω οτι αν ξ1=ξ2=ξ του πρωτου ερωτηματος βγαζει 2+1=3 αλλα σιγα μην βγαινει ετσι
Μάρκος Βασίλης
Πολύ δραστήριο μέλος
Ο Βασίλης αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 28 ετών, Διδακτορικός και μας γράφει από Καισαριανή (Αττική). Έχει γράψει 1,871 μηνύματα.

26-04-20

21:51
View attachment 69314
Είμαι 99% σίγουρος πως στο β χρησιμοποιώ το ξ του Α και κάνω 2 ΘΜΤ αλλά δεν μου βγαίνουν οι πράξεις
Για το β') ερώτημα, μπορείς να πάρεις
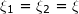
Όπως και να έχει, είναι τελείως κλασσική άσκηση το β') ερώτημα. Για τα διευκολυνθούμε, ας γράψουμε λίγο το ζητούμενο ως εξής:
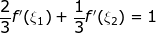
Τώρα μυριζόμαστε ότι πρέπει να σπάσουμε το [1,3] σε δύο τμήματα, στο πρώτο να δώσουμε τα 2/3 του μήκους και στο δεύτερο το 1/3. Έτσι, σπάμε το [1,3] στα [1,7/3] και [7/3,3]. Τώρα, η f ικανοποιεί τις υποθέσεις του ΘΜΤ και στα δύο οπότε βρίσκουμε
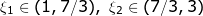
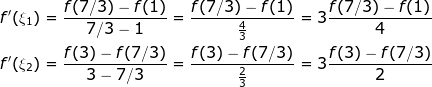
Τώρα, βλέπουμε ότι:
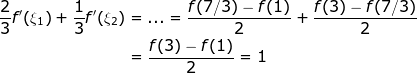
που ήταν το ζητούμενο.
Είναι κλασσικές ασκήσεις αυτές, προσοχή - όχι ότι έχουν ενδιαφέρον, αλλά είναι κρίμα να χάσεις μονάδες από τα στανταράκια.
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11,341 μηνύματα.

26-04-20

22:37
Παραθέτω μια ακόμη λύση,σε περίπτωση που κάποιος έκανε διαφορετικά τον διαχωρισμό του χωρίου :
f συνεχής στο [1,3] & παραγωγίσιμη στο (1,3) και η Cf διέρχεται
απο Α(1,1) & Β(3,3) .
Εντάξει το α ήταν πανεύκολο αλλά είμαι τυπικός και το βάζω να υπάρχει εαν τυχόν κάποιο άλλο παιδί χρειαστεί βοήθεια :
α)
Ζητάω εφαπτομένη στο Μ(ξ,f(ξ)) ,οπου ξ Ε (1,3) :
η y = -x -1 να είναι κάθετη σε αυτή .
Αρκεί :
λεφ*λε = -1 =>
λεφ*(-1) = -1 =>
λεφ = 1 =>
f '(ξ) = 1
Εφόσον ισχύουν οι προυποθέσεις για την εφαρμογή του ΘΜΤ
στο διάστημα [1,3] συμπεραίνουμε οτι υπάρχει ξ Ε (1,3) :
f '(ξ) = [f(3)-f(1)] / (3-1) = (3-1)/(3-1) = 1
Επειδή f(1) =1 & f(3) = 3 απο τα δεδομένα μας .
y - f(ξ) = x-ξ =>
f(ξ) = y-x+ξ
f συνεχής στο [1,3] & παραγωγίσιμη στο (1,3) και η Cf διέρχεται
απο Α(1,1) & Β(3,3) .
Εντάξει το α ήταν πανεύκολο αλλά είμαι τυπικός και το βάζω να υπάρχει εαν τυχόν κάποιο άλλο παιδί χρειαστεί βοήθεια :
α)
Ζητάω εφαπτομένη στο Μ(ξ,f(ξ)) ,οπου ξ Ε (1,3) :
η y = -x -1 να είναι κάθετη σε αυτή .
Αρκεί :
λεφ*λε = -1 =>
λεφ*(-1) = -1 =>
λεφ = 1 =>
f '(ξ) = 1
Εφόσον ισχύουν οι προυποθέσεις για την εφαρμογή του ΘΜΤ
στο διάστημα [1,3] συμπεραίνουμε οτι υπάρχει ξ Ε (1,3) :
f '(ξ) = [f(3)-f(1)] / (3-1) = (3-1)/(3-1) = 1
Επειδή f(1) =1 & f(3) = 3 απο τα δεδομένα μας .
y - f(ξ) = x-ξ =>
f(ξ) = y-x+ξ
aggelosst9
Εκκολαπτόμενο μέλος
Ο aggelosst9 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Φοιτητής του τμήματος Οικονομικής Επιστήμης Ο.Π.Α. (Αθήνα). Έχει γράψει 125 μηνύματα.

27-04-20

00:18
Οκ παίδες ευχαριστώ πολύ, με καλύψατε, επειδή το α έβγαινε τόσο εύκολα λέω θα χρειαστεί και στο β, για αυτό το παρέθεσα.
Έψαχνα να κάνω κάτι με το ξ του α γιατί στο 99% των ασκήσεων το πηγαίναμε έτσι όλη τη χρονιά.. είχα δει και το σπάσιμο σε τμήματα έτσι αλλά μάλλον ήταν στο ΠΟΛΥ πίσω μέρος του μυαλού μου :pΓια το β') ερώτημα, μπορείς να πάρειςκαι να τελειώνεις, αλλά φαντάζομαι δεν ήταν αυτή η πρόθεση. Έπρεπε, βέβαια, να γράφει στην εκφώνηση «διαφορετικά μεταξύ τους» ή κάτι άλλο.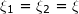
Όπως και να έχει, είναι τελείως κλασσική άσκηση το β') ερώτημα. Για τα διευκολυνθούμε, ας γράψουμε λίγο το ζητούμενο ως εξής:
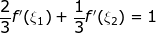
Τώρα μυριζόμαστε ότι πρέπει να σπάσουμε το [1,3] σε δύο τμήματα, στο πρώτο να δώσουμε τα 2/3 του μήκους και στο δεύτερο το 1/3. Έτσι, σπάμε το [1,3] στα [1,7/3] και [7/3,3]. Τώρα, η f ικανοποιεί τις υποθέσεις του ΘΜΤ και στα δύο οπότε βρίσκουμετέτοια ώστε: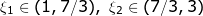
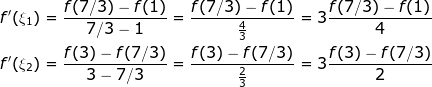
Τώρα, βλέπουμε ότι:
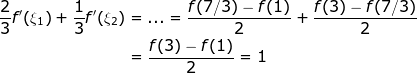
που ήταν το ζητούμενο.
Είναι κλασσικές ασκήσεις αυτές, προσοχή - όχι ότι έχουν ενδιαφέρον, αλλά είναι κρίμα να χάσεις μονάδες από τα στανταράκια.
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3,928 μηνύματα.

27-04-20

02:09
δεν νομιζω φιλε μου οτι ειναι πολυ σωστο το επιχειρημα οτι απο μια ριζα να γενικευσεις την συναρτηση.και γτ να μην ειναι ριζα μιας αλλης συναρτησης?Παραθέτω μια ακόμη λύση,σε περίπτωση που κάποιος έκανε διαφορετικά τον διαχωρισμό του χωρίου :
f συνεχής στο [1,3] & παραγωγίσιμη στο (1,3) και η Cf διέρχεται
απο Α(1,1) & Β(3,3) .
Εντάξει το α ήταν πανεύκολο αλλά είμαι τυπικός και το βάζω να υπάρχει εαν τυχόν κάποιο άλλο παιδί χρειαστεί βοήθεια :
β) ΘΜΤ στο [1,ξ] & [ξ,3] ,άρα υπάρχουν ξ1 Ε (1,ξ) & (ξ,3) τέτοια ώστε :α)
Ζητάω εφαπτομένη στο Μ(ξ,f(ξ)) ,οπου ξ Ε (1,3) :
η y = -x -1 να είναι κάθετη σε αυτή .
Αρκεί :
λεφ*λε = -1 =>
λεφ*(-1) = -1 =>
λεφ = 1 =>
f '(ξ) = 1
Εφόσον ισχύουν οι προυποθέσεις για την εφαρμογή του ΘΜΤ
στο διάστημα [1,3] συμπεραίνουμε οτι υπάρχει ξ Ε (1,3) :
f '(ξ) = [f(3)-f(1)] / (3-1) = (3-1)/(3-1) = 1
Επειδή f(1) =1 & f(3) = 3 απο τα δεδομένα μας .
y - f(ξ) = x-ξ =>
f(ξ) = y-x+ξ
f '(ξ1) = [f(ξ)-f(1)] / (ξ-1) = [f(ξ)-1]/(ξ-1)
f '(ξ2) = [f(3)-f(ξ)] / (3-ξ) = [3-f(ξ)]/(3-ξ) = [f(ξ)-3]/(ξ-3)
2f '(ξ1) +f '(ξ2) = [2f(ξ)-2]/(ξ-1) + [f(ξ)-3]/(ξ-3)
= [(2f(ξ)-2)(ξ-3) + (f(ξ)-3)(ξ-1)]/(ξ-1)(ξ-3)
= [ 2ξf(ξ) - 6f(ξ) -2ξ +6 +ξf(ξ) -f(ξ) -3ξ +3] /(ξ-1)(ξ-3)
=[ 3ξf(ξ) - 7f(ξ) -5ξ +9]/(ξ-1)(ξ-3)
Όμως βρήκαμε προηγουμένως ότι :
f '(ξ) = 1 όπου το ξ είναι μια λύση της γενικότερης εξίσωσης :
f '(x) -1 = 0 =>
Εφόσον η προηγούμενη ισχύει με ολοκλήρωση δεξιά και αριστερά, βρίσκουμε οτι θα ισχύει και η σχέση :
f(x)-x = c
Για να βρούμε το c απλά αντικαθιστούμε μια γνωστή τιμή της f(x) ,π.χ. για x =1 έχουμε :
f(1)-1 = c =>
1 -1 = c =>
c= 0
Τελικά :
f(x) = x
Επίσης για x = ξ η παραπάνω εξίσωση γίνεται :
f(ξ) = ξ
Καταλήγουμε εν τέλει οτι :
2f '(ξ1) +f '(ξ2) = [ 3ξf(ξ) - 7f(ξ) -5ξ +9]/(ξ-1)(ξ-3) = [ 3ξ² -7ξ -5ξ +9] /(ξ-1)(ξ-3) = [3ξ²-12ξ+9]/(ξ-1)(ξ-3)
= 3(ξ²-4ξ+3)/(ξ-1)(ξ-3) = 3(ξ-1)(ξ-3)/(ξ-1)(ξ-3) = 3
Και άρα αποδείξαμε το ζητούμενο .
Σημείωση θέλει πολύ προσοχή στην κατανόηση των βημάτων και γιατί η παραπάνω λύση λειτουργεί για να μην παρεξηγήσουμε ορισμένα επιχειρήματα κατά την διαδικασία . Η σχέση f(x) = x που προέκυψε σε καμία περίπτωση δεν σημαίνει οτι η συνάρτηση του προβλήματος μας είναι απαραίτητα μια ευθεία .
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11,341 μηνύματα.

27-04-20

12:14
δεν νομιζω φιλε μου οτι ειναι πολυ σωστο το επιχειρημα οτι απο μια ριζα να γενικευσεις την συναρτηση.και γτ να μην ειναι ριζα μιας αλλης συναρτησης?
Ναι , έχεις δίκιο , μεγάλο μου λάθος,το επιχείρημα για την μετάβαση στην γενικότερη εξίσωση δεν στέκει γιατί αποδείξαμε οτι ισχύει για τουλάχιστον ένα ξ Ε (1,ξ) και όχι οτι ισχύει καθολικά οτι f '(x) = 1.
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3,928 μηνύματα.

27-04-20

13:53
δεν πειραζει.ουδεις ασφαλτος που λεει και η ατζελαΝαι , έχεις δίκιο , μεγάλο μου λάθος,το επιχείρημα για την μετάβαση στην γενικότερη εξίσωση δεν στέκει γιατί αποδείξαμε οτι ισχύει για τουλάχιστον ένα ξ Ε (1,ξ) και όχι οτι ισχύει καθολικά οτι f '(x) = 1.
Αυτόματη ένωση συνεχόμενων μηνυμάτων:
Να αποδειχθει η προταση:TO μεγιστο ειναι το μεγαλυτερο απο τα τοπικα μεγιστα.Δεν μου φαινεται και πολυ σωστη προταση
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11,341 μηνύματα.

27-04-20

14:28
δεν πειραζει.ουδεις ασφαλτος που λεει και η ατζελα
Αυτόματη ένωση συνεχόμενων μηνυμάτων:
Να αποδειχθει η προταση:TO μεγιστο ειναι το μεγαλυτερο απο τα τοπικα μεγιστα.Δεν μου φαινεται και πολυ σωστη προταση
Πράγματι, σε ευχαριστώ για την παρατήρηση
 .
.Ούτε εγώ καταλαβαίνω ακριβώς την πρόταση, εφόσον το μέγιστο ορίζεται έτσι ώστε να είναι το μεγαλύτερο απο όλα τα τοπικά μέγιστα .
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3,928 μηνύματα.

27-04-20

14:40
το τοπικο μεγιστο μπορει να ιεναι μικροτερο απο τοπικο ελαχιστοΠράγματι, σε ευχαριστώ για την παρατήρηση.
Ούτε εγώ καταλαβαίνω ακριβώς την πρόταση, εφόσον το μέγιστο ορίζεται έτσι ώστε να είναι το μεγαλύτερο απο όλα τα τοπικά μέγιστα .
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11,341 μηνύματα.

27-04-20

14:47
το τοπικο μεγιστο μπορει να ιεναι μικροτερο απο τοπικο ελαχιστο
Δεν διαφωνώ με αυτό ωστόσο η πρόταση σου λέει οτι η σύγκριση γίνεται μεταξύ μέγιστου και τοπικών μέγιστων , όχι με τοπικά ελάχιστα .
Οπότε εαν ένα τοπικό μέγιστο είναι μικρότερο απο το τοπικό ελάχιστο,και πάλι δεν αναιρεί το γεγονός πως και φυσικά τόσο αυτό το τοπικό μέγιστο αλλά και αυτό το τοπικό ελάχιστο θα είναι μικρότερα απο το μέγιστο . Είναι ο ορισμός του μέγιστου μιας συνάρτησης.
Μάρκος Βασίλης
Πολύ δραστήριο μέλος
Ο Βασίλης αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 28 ετών, Διδακτορικός και μας γράφει από Καισαριανή (Αττική). Έχει γράψει 1,871 μηνύματα.

27-04-20

19:46
Πράγματι, σε ευχαριστώ για την παρατήρηση.
Ούτε εγώ καταλαβαίνω ακριβώς την πρόταση, εφόσον το μέγιστο ορίζεται έτσι ώστε να είναι το μεγαλύτερο απο όλα τα τοπικά μέγιστα .
Ορισμός: Αν




Ορισμός: Αν





Οι ορισμοί είναι ξεχωριστοί και ο ένας δεν κάνει αναφορά στον άλλον. Απλώς, είναι τετριμμένο να αποδείξεις ότι ένα (ολικό) μέγιστο είναι και τοπικό. Τετριμμένο, μεν, αλλά θέλει απόδειξη (προφανώς εκτός λυκείου αυτά, στο λύκειο θεωρείται προφανές).
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3,928 μηνύματα.

27-04-20

19:57
παρε πχ τη συναρτηση f(x)=(x-1)/e^x εχει τοπικο μεγιστο στο χ=2 το οποιο ομως ειναι και ολικο.εκει τι να αποδειξεις.να παρεις τα ορια στο -00 και στο +00.ψιλοαυτονοητο
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 24 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 226 μέλη διάβασαν αυτό το θέμα:
- trifasikodiavasma
- haji
- thepigod762
- Mariosm.
- soulatso
- oteletampis
- phleidhs
- Hased Babis
- AggelikiGr
- sir ImPeCaBlE
- veiNqh
- Scandal
- alekos
- Debugging_Demon
- just some guy
- xristosgkm
- ismember
- Apocalypse
- arrow25
- rempelos42
- ggl
- GStef
- QWERTY23
- xrisamikol
- Σωτηρία
- nikoletaz57
- _Aggelos123
- Mariam38
- SlimShady
- strsismos88
- Georgekk
- Lia 2006
- igeorgeoikonomo
- marian
- tsiobieman
- constansn
- Xristosdimitra
- Panagiotis849
- ρενακι 13
- Memetchi
- eukleidhs1821
- Nikkkpat
- Unboxholics
- korlef
- kwstaseL
- Thanos_D
- the purge
- T C
- Giii
- Papachrist
- liaiscool
- Αννα Τσιτα
- globglogabgalab
- Pharmacist01
- thanahss
- abcdefg12345
- nicole1982
- thecrazycretan
- kvstas92
- KingOfPop
- maria301
- papa2g
- stefan
- Κλημεντίνη
- TonyMontanaEse
- Athens2002
- Alexecon1991
- Μάρκος Βασίλης
- Cortes
- το κοριτσι του μαη
- calliope
- ale
- panagiotis G
- Kleanth
- aggelosst9
- BioChemical
- spring day
- nucomer
- Georgia110
- LeoDel
- pink_panther
- Alexandros973
- marsenis
- den antexw allh apotyxia
- KaterinaL
- kiyoshi
- drosos
- Λαμπρινηη
- Bill22
- Chrysablac.
- giorgosp97
- Βλα
- Monster Hunter
- jul25
- xxxtolis
- Stroka
- nicks1999
- totiloz
- Earendil
- mitsakos
- tasost
- lnesb
- ssalex
- Vasilina93
- alan09
- Livaja10
- χημεια4λαιφ
- Viedo
- UncleJ
- Kostakis45
- Infrared
- Zgian
- pepatogourounaki
- hirasawayui
- GeoCommand
- Eleni54
- American Economist
- EiriniS20
- ΘανάσοςG4
- stamoul1s
- Αριάνα123
- uni77
- Libertus
- tasoss
- PanosCh002
- Unseen skygge
- Νικόλας Ραπ.
- cel123
- The Limit Does Not Exist
- don_vito
- suaimhneas
- Αλκης Κ.
- alexrami
- Baggelitsa36
- Νομικάριος13
- spinalgr1990
- d_th
- Adolfo valencia
- Πα.Κ
- Vasilis25
- Johnman97
- Steffie88
- rekcoR
- gwgw_5
- fockos
- Mariahj
- roud
- kostas83
- Cpt.Philips
- Makis45
- Χρησλου
- Panos_02
- Vold
- tymvorixos
- GiorgosAsi
- Neos167
- theodoraooo
- George187
- Άρτεμις Α.
- Μαρία2222
- christos87
- Idontknoww
- jimis2001
- Metamorph
- Γατόπαρδος.
- Johnsk
- mitsos14
- johnsiak
- Elel
- Dreamer_SW
- Γιαννης1987Θεσσ
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki

