Συλλογή ασκήσεων και τεστ στα Μαθηματικά Προσανατολισμού

panabarbes · 10-11-13

Δίνεται συνάρτηση $\mathit{f}:R\rightarrow R$ , με $\mathit{f\left(R \right)}=R$ για την οποία ισχύει:
${f}^{5} (x)+3f(x) = x-2$ , για κάθε $x\epsilon R$

i. Να μελετήσετε την $\mathit{f}$ ως προς την μονοτονία.

ii. Να δείξετε ότι η $\mathit{f}$ αντιστρέφεται και να βρείτε την ${f}^{-1}$

iii. Έστω $z\epsilon C$ για τον οποίο ισχύει:

$f\left(\left|z+2 \right| \right) - f\left(\left|z+4i \right| \right) = f(2)$

Να βρείτε τη γραμμή στην οποία ανήκει η εικόνα του $\mathit{z}$ στο μιγαδικό επίπεδο.

Guest 018946 · 10-11-13

g(x)=x^5+3x
g γν αυξουσα

gof(x) γν αυξουσα

χ1>χ2

gof(x1)>gof(x2) <=> f(x1)>f(x2)

αρα φ γν αυξουσα αρα 1-1 αρα αντιστρεψιμη
θετω y=f(x)

x=2+f^5(x)+3f(x) ,x \in R
thus f^(-1)(x)=x^5+3x+2 , x \in R

ii) f(2)=0

|z+2|=|z+4i| και μετα θεσιμο και πραξειιιιιις

tipotas · 10-11-13

Αρχική Δημοσίευση από styt_geia:
Θεωρούμε την συνάρτηση $f(x)=\max\left\{x^3, \cos^2 x \right\}$ .
i) Nα δείξετε ότι υπάρχει μοναδικό $\xi \in \left(0, \frac{\pi}{2} \right)$ τέτοιο ώστε $\xi^3=\cos^2 \xi$
ii) Να δείξετε ότι $f(\xi)= \min f(x)$ στο $\left[0,\frac{\pi}{2}\right]$
iii) Να βρεθεί το πλήθος των ριζών της εξίσωσης $f(x)=\lambda$ για κάθε τιμή της παραμέτρου $\lambda \in \left[0,\frac{\pi^3}{8}\right]$

*Το cos δηλώνει το συνημίτονο

Καλησπέρα, μπορείς να εξηγήσεις την f(x) επειδή δεν κατάλαβα τη εννοείς;

rebel · 11-11-13

Αρχική Δημοσίευση από tipotas:
Καλησπέρα, μπορείς να εξηγήσεις την f(x) επειδή δεν κατάλαβα τη εννοείς;

Καλημέρα. Το max δύο αριθμών είναι ο μέγιστος από αυτούς. Στην περίπτωσή μας έστω $x_0 \in \ \left[ 0, \frac{\pi}{2} \right]$ . Τότε $f(x_0)=x_0^3$ αν $x_0^3 \geq \cos x_0^2$ ενώ $f(x_0)=\cos x_0^2$ αν $x_0^3 < \cos x_0^2$

nikoslarissa · 12-11-13

Δίνεται συνάρτηση $f$ γνησίως αύξουσα στο $R$ με $f(-1)>0$ και ο μιγαδικός αριθμός $z=\frac{f(-1)f(0)}{2}+\frac{4\sqrt{3}}{f(1)}i$ ,για τον οποίο ισχύει ότι $\left|z \right|=\frac{z}{2}(1-\sqrt{3}i)$ .Να αποδείξετε ότι:

α) $f(-1)f(0)f(1)=8$

β) $2Re(z)=\left|z \right|$

γ) $f(-1)<2<f(1)$

δ)η f αντιστρέφεται και ισχύει $-1<{f}^{-1}(\sqrt{\left|z \right|})<0$

panabarbes · 12-11-13

Αρχική Δημοσίευση από nikoslarissa:
Δίνεται συνάρτηση $f$ γνησίως αύξουσα στο $R$ με $f(-1)>0$ και ο μιγαδικός αριθμός $z=\frac{f(-1)f(0)}{2}+\frac{4\sqrt{3}}{f(1)}i$ ,για τον οποίο ισχύει ότι $\left|z \right|=\frac{z}{2}(1-\sqrt{3}i)$ .Να αποδείξετε ότι:

α) $f(-1)f(0)f(1)=8$

β) $2Re(z)=\left|z \right|$

γ) $f(-1)<2<f(1)$

δ)η f αντιστρέφεται και ισχύει $-1<{f}^{-1}(\sqrt{\left|z \right|})<0$

Σκεφτόμουν να την βάλω αυτήν την άσκηση! Με πρόλαβες!

Guest 018946 · 13-11-13

το 1) ειναι πραξεις και λες το δευτερο μελος πρεπει να ειναι πραγματικο και μηδενιζεις το φανταστικο μερος του δεξιου μιγα

2)πραξεις
3) εστω φ(1)=<2 <=> 4 <φ(-1)φ(0)

λογω γν αυξουσοτητας 0<φ(0)<2
0<φ(-1)<2
πολζω κατα μελη παιρνω ατοπο εντελως ομοια για την αλλη

4) αφου γν αυξουσα θα ειναι και 1-1 αρα θα αντιστρεφεται

ισοδυναμα δηλαδη εχω

-1<f^(-1)(\sqrt(f(-1)f(0))<0

f αρω
αφου η φ γν αυξουσα κραταω φορες
κ μετα τετραγωνιζω να πουμε
και παω φ^2(-1)<φ(0)φ(-1)<φ(0)

παω ξεχωριστα σε καθεμια και εχω φ(-1)<φ(0) αφου φ γν αυξουσα ισχυει

ομοια για την δεξια και τελοιωσαμε

tipotas · 14-11-13

Αρχική Δημοσίευση από styt_geia:
Καλημέρα. Το max δύο αριθμών είναι ο μέγιστος από αυτούς. Στην περίπτωσή μας έστω $x_0 \in \ \left[ 0, \frac{\pi}{2} \right]$ . Τότε $f(x_0)=x_0^3$ αν $x_0^3 \geq \cos x_0^2$ ενώ $f(x_0)=\cos x_0^2$ αν $x_0^3 < \cos x_0^2$

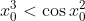
οκ ευχαριστώ

Guest 018946 · 20-11-13

"ένα μινι δωράκι"

Αν h συνεχής συνάρτηση στο R και η εξίσωση h(x)=x είναι αδύνατη, τότε να δείξετε ότι και η εξίσωση h(h(x))=x είναι
επίσης αδύνατη ,

Civilara · 20-11-13

Αρχική Δημοσίευση από dr.tasos:
"ένα μινι δωράκι"

Αν h συνεχής συνάρτηση στο R και η εξίσωση h(x)=x είναι αδύνατη, τότε να δείξετε ότι και η εξίσωση h(h(x))=x είναι
επίσης αδύνατη ,

Θεωρούμε την συνάρτηση g με τύπο g(x)=h(x)-x. Επειδή η h είναι συνεχής στο R τότε και η g είναι συνεχής στο R. Επειδή ισχύει h(x) διάφορο x για κάθε x ανήκει R τότε ισχύει g(x) διάφορο 0 για κάθε x ανήκει R και επειδή η g είναι συνεχής στο R τότε η g διατηρεί σταθερό πρόσημο στο R. Συνεπώς g(x)>0 για κάθε x ανήκει R ή g(x)<0 για κάθε x ανήκει R.

Η σύνθετη συνάρτηση goh με τύπο (goh)(x)=g(h(x))=h(h(x))-h(x) είναι συνεχής στο R καθώς οι h και g είναι συνεχείς στο R.

(i) Αν g(x)>0 τότε g(h(x))>0 για κάθε x ανήκει R. Έχουμε:
g(x)>0 => h(x)-x>0 => h(x)>x
g(h(x))>0 => h(h(x))-h(x)>0 => h(h(x))>h(x)
Επειδή h(h(x))>h(x)>x τότε h(h(x))>x για κάθε x ανήκει R

(ii) Αν g(x)<0 τότε g(h(x))<0 για κάθε x ανήκει R. Έχουμε:
g(x)<0 => h(x)-x<0 => h(x)<x
g(h(x))<0 => h(h(x))-h(x)<0 => h(h(x))<h(x)
Επειδή h(h(x))<h(x)<x τότε h(h(x))<x για κάθε x ανήκει R

Συνεπώς h(h(x)) διάφορο x για κάθε x ανήκει R.

Guest 018946 · 20-11-13

η λυση που εκανα ηταν με ατοπο εστω οτι εξισωση δεν ηταν αδυνατη θα υπηρχε χ0 τ.ω. : η(η(χ0))=χ0
μετα στην g που εθεσες βαζω μια το χ0 και μετα μια το η(χ0) αρα απο θετ θα υπηρχε ξ τ.ω. η(ξ)=ξ
ατοπο αφου ξερω οτι αυτο το πραμα ειναι αδυνατο

Guest 018946 · 20-11-13

Αρχική Δημοσίευση από styt_geia:
Έστω $f:[1,4]\rightarrow(0,+\infty)$ συνεχής με $f^{3}(4)=f(1)f(2)f(3)$ . Να εξεταστεί αν η f είναι 1-1

Γιαυτην μπορουμε να πουμε οτι εστω οτι ειναι 1-1 τοτε θα ειναι και γν μονοτονη

Χωρις βλαβη θεωρω οτι ειναι γν αυξουσα φ(4)>φ(1)
φ(4)>φ(2)
φ(4) >φ(3)

πολ/ζω κατα μελη ( ολα θετικα ) και έχω άτοπο

αρα φ δεν ειναι 1-1

panabarbes · 21-11-13

Αρχική Δημοσίευση από dr.tasos:
Γιαυτην μπορουμε να πουμε οτι εστω οτι ειναι 1-1 τοτε θα ειναι και γν μονοτονη

Χωρις βλαβη θεωρω οτι ειναι γν αυξουσα φ(4)>φ(1)
φ(4)>φ(2)
φ(4) >φ(3)

πολ/ζω κατα μελη ( ολα θετικα ) και έχω άτοπο

αρα φ δεν ειναι 1-1

Μην ξεχάσεις να παραθέσεις και την άλλη περίπτωση της γν. φθίνουσας σε κάποιο τεστ!

Guest 018946 · 21-11-13

Γιαυτο έβαλα και το χωρις βλάβη

rebel · 21-11-13

Αρχική Δημοσίευση από dr.tasos:
Γιαυτην μπορουμε να πουμε οτι εστω οτι ειναι 1-1 τοτε θα ειναι και γν μονοτονη

Έχω την εντύπωση ότι και αυτό θέλει απόδειξη.

Guest 018946 · 21-11-13

Οντως θελει αποδειξη Κωστα.

Διονύσης13 · 21 Νοεμβρίου 2013

Το έκανα σήμερα στο σχολείο, δεν το δέχτηκε χωρίς απόδειξη. Οπότε κάντε τη

Η απόδειξη βέβαι είναι λίγο μπελαλίδικη, οπότε το βγάζεις με Bolzano.

tipotas · 21-11-13

Που τις βρίσκετε αυτές τις ασκήσεις;

panabarbes · 21-11-13

Σε βιβλία

tipotas · 22-11-13

Αυτό εννοείται!
Εννοώ σε πια βιβλία

Συλλογή ασκήσεων και τεστ στα Μαθηματικά Προσανατολισμού

Εκκολαπτόμενο μέλος

Guest 018946

Επισκέπτης

Εκκολαπτόμενο μέλος

Πολύ δραστήριο μέλος

Δραστήριο μέλος

Εκκολαπτόμενο μέλος

Guest 018946

Επισκέπτης

Εκκολαπτόμενο μέλος

Guest 018946

Επισκέπτης

Περιβόητο μέλος

Guest 018946

Επισκέπτης

Guest 018946

Επισκέπτης

Εκκολαπτόμενο μέλος

Guest 018946

Επισκέπτης

Πολύ δραστήριο μέλος

Guest 018946

Επισκέπτης

Τιμώμενο Μέλος

Εκκολαπτόμενο μέλος

Εκκολαπτόμενο μέλος

Εκκολαπτόμενο μέλος