Helen06
Δραστήριο μέλος
Η Helen06 αυτή τη στιγμή είναι συνδεδεμένη. Είναι 19 ετών και Φοιτήτρια του τμήματος Πληροφοριακά Συστήματα Μακεδονίας. Έχει γράψει 531 μηνύματα.

22-07-23

16:54
Γειά σας θα ήθελα μια βοήθεια στις παρακάνω ασκήσεις. Η πρώτη είναι με τις δίκλαδες (η φώτο) και η δεύτερη είναι: να αποδείξω ότι η συνάρτηση (απόλυτο του χ-2)+1 δεν είναι 1-1. Το μόνο που κατάλαβα είναι ότι πρέπει να πάρω δύο τυχαία χ1<>χ2 και να αποδείξω f(x1)=f(x2). Υπάρχει κάποιος άλλος τρόπος;

eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.965 μηνύματα.

22-07-23

18:34
ωραια ερωτηματακια να καταλαβει καποιος τη θεωρια που στις πανελληνιες τα αποφευγουν για καποιον περιεργο λογο.για την απολυτο(χ-2)+1 μπορεις να παρεις ξερω γω χ1=1 f(1)=2 και χ1=3 f(3)=2 επομενως δεν ισχυει ο ορισμος και δεν ειναι 1-1.Αυτο που εκανα ειναι το λεγομενο αντιπαραδειγμα στα μαθηματικα.Γειά σας θα ήθελα μια βοήθεια στις παρακάνω ασκήσεις. Η πρώτη είναι με τις δίκλαδες (η φώτο) και η δεύτερη είναι: να αποδείξω ότι η συνάρτηση (απόλυτο του χ-2)+1 δεν είναι 1-1. Το μόνο που κατάλαβα είναι ότι πρέπει να πάρω δύο τυχαία χ1<>χ2 και να αποδείξω f(x1)=f(x2). Υπάρχει κάποιος άλλος τρόπος;
View attachment 118830
Τωρα,για τις 2 δικλαδες η δευτερη απο κατω που εχει ριζα παλι με αντιπαραδειγμα δεν ειναι 1-1 διοτι αν παρεις χ1=3 και χ2=0 θα σου βγαλουν την ιδια τιμη 1.Για την πρωτη ειναι 1-1 και πρεπει να το βγαλεις με τον ορισμο ειτε με μονοτονια αλλα κατασκευαστικα.Καλυτερα να το παμε με μονοτονια για πιο ευκολα.Η πρωτος κλαδος ευκολα ειναι γνησιως αυξουσα,ο δευτερος κλαδος επισης ευκολα ειναι γνησιως αυξουσα.Το θεμα ειναι πως θα δειξεις οτι ειναι και στην ενωση γτ προφανως θα ξερεις οτι f γνησιως αυξουσα στο Δ1 και γνησιως αυξουσα στο Δ2 δεν ειναι γνησιως αυξουσα κατ αναγκη και στο Δ1ενωσηΔ2.Πολυ ευκολα ομως διαπιστωνεται οτι ισχυει και στην ενωση γτ αν παρεις χ1 στον αριστερο κλαδο τα f(x1) ειναι αρνητικα και χ2 στον δεξιο κλαδο τα f(x2)>0 επομενως ισχυει ο ορισμος!Επομενως,γνησιως αυξουσα σε ολο το πεδιο ορισμου αρα και 1-1.Μπορουσες φυσικα να το πηγαινες με χ1 διαφορο του χ2 χωρις τη χρηση μονοτονιας αλλα καλο ειναι και ετσι για εκπαιδευτικους λογους.
Κατι ιδιαιτερο για αυτη τη συναρτηση οτι δεν μπορεις να εφαρμοσεις το θεωρημα με τις παραγωγους στην ενωση καθω στο μηδεν η συναρτηση δεν ειναι συνεχης!
Helen06
Δραστήριο μέλος
Η Helen06 αυτή τη στιγμή είναι συνδεδεμένη. Είναι 19 ετών και Φοιτήτρια του τμήματος Πληροφοριακά Συστήματα Μακεδονίας. Έχει γράψει 531 μηνύματα.

22-07-23

18:54
Τέλεια σ'ευχαριστώ πάρα πολύ. Και εγώ αυτό έκανα στη δίκλαδη μόνο που μετά δε μπόρεσα να βρω για όλη την F(X). Ωστόσο στο β) πως ξέρω ότι όντως δεν είναι 1-1, πρέπει πριν να ξεκινήσω να τη λύνω να δοκιμάζω αυτό με τους τυχαίους αριθμούς;ωραια ερωτηματακια να καταλαβει καποιος τη θεωρια που στις πανελληνιες τα αποφευγουν για καποιον περιεργο λογο.για την απολυτο(χ-2)+1 μπορεις να παρεις ξερω γω χ1=1 f(1)=2 και χ1=3 f(3)=2 επομενως δεν ισχυει ο ορισμος και δεν ειναι 1-1.Αυτο που εκανα ειναι το λεγομενο αντιπαραδειγμα στα μαθηματικα.
Τωρα,για τις 2 δικλαδες η δευτερη απο κατω που εχει ριζα παλι με αντιπαραδειγμα δεν ειναι 1-1 διοτι αν παρεις χ1=3 και χ2=0 θα σου βγαλουν την ιδια τιμη 1.Για την πρωτη ειναι 1-1 και πρεπει να το βγαλεις με τον ορισμο ειτε με μονοτονια αλλα κατασκευαστικα.Καλυτερα να το παμε με μονοτονια για πιο ευκολα.Η πρωτος κλαδος ευκολα ειναι γνησιως αυξουσα,ο δευτερος κλαδος επισης ευκολα ειναι γνησιως αυξουσα.Το θεμα ειναι πως θα δειξεις οτι ειναι και στην ενωση γτ προφανως θα ξερεις οτι f γνησιως αυξουσα στο Δ1 και γνησιως αυξουσα στο Δ2 δεν ειναι γνησιως αυξουσα κατ αναγκη και στο Δ1ενωσηΔ2.Πολυ ευκολα ομως διαπιστωνεται οτι ισχυει και στην ενωση γτ αν παρεις χ1 στον αριστερο κλαδο τα f(x1) ειναι αρνητικα και χ2 στον δεξιο κλαδο τα f(x2)>0 επομενως ισχυει ο ορισμος!Επομενως,γνησιως αυξουσα σε ολο το πεδιο ορισμου αρα και 1-1.Μπορουσες φυσικα να το πηγαινες με χ1 διαφορο του χ2 χωρις τη χρηση μονοτονιας αλλα καλο ειναι και ετσι για εκπαιδευτικους λογους.
Κατι ιδιαιτερο για αυτη τη συναρτηση οτι δεν μπορεις να εφαρμοσεις το θεωρημα με τις παραγωγους στην ενωση καθω στο μηδεν η συναρτηση δεν ειναι συνεχης!
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.965 μηνύματα.

22-07-23

18:59
οχι ρε συ τι να λυσεις με τυχαιους αριθμους!Αυτο ειναι το νοημα του αντιπαραδειγματος.Αν βρεις 2 αριθμους που βγαζουν ιδια συναρτησιακη τιμη σου κατοχυρωνει οτι δεν ειναι 1-1!!Αυτο γινεται γτ ο ορισμος του 1-1 σου λεει για καθε χ1,χ2 επομενως εσυ το αρνεισαι αυτο και θες να δεις αν υπαρχουν 2 τουλαχιστον χ1,χ2 που σου βγαζουν ιδια συναρτησιακη τιμη.Οσο για το πρωτο εκει ειναι η πονηραδα να βγαλεις με τον ορισμο οτι ειναι και στην ενωση f(x1)<f(x2) που ειναι ευκολο ομως γτ αν παρεις χ1 στον ενα κλαδο,χ2 στον αλλο κλαδο ειναι προφανης η διαταξη.Τέλεια σ'ευχαριστώ πάρα πολύ. Και εγώ αυτό έκανα στη δίκλαδη μόνο που μετά δε μπόρεσα να βρω για όλη την F(X). Ωστόσο στο β) πως ξέρω ότι όντως δεν είναι 1-1, πρέπει πριν να ξεκινήσω να τη λύνω να δοκιμάζω αυτό με τους τυχαίους αριθμούς;
Cade
Πολύ δραστήριο μέλος
Ο Cade αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Απόφοιτος λυκείου. Έχει γράψει 872 μηνύματα.

22-07-23

19:34
Άλλος τρόπος για την 2 είναι με τον ορισμό:
Για κάθε x1, x2∈R με f(x1)=f(x2) ισχύει:
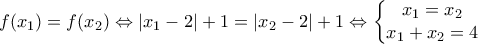
οπότε μπορούμε να βρούμε άπειρα ζεύγη (x1,x2) με διαφορετικά χ, τα οποία δίνουν την ίδια εικόνα.
Για κάθε x1, x2∈R με f(x1)=f(x2) ισχύει:
οπότε μπορούμε να βρούμε άπειρα ζεύγη (x1,x2) με διαφορετικά χ, τα οποία δίνουν την ίδια εικόνα.
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 26 ετών, Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 12.152 μηνύματα.

22-07-23

20:03
Εννοεί βασικά οτι επιλέγεις τυχαία δύο αριθμούς για το αντιπαράδειγμα . Οτι δεν υπάρχει συστηματικός τρόπος να εντοπίσεις ποιοι δύο αριθμοί θα δουλέψουν . Και έχει δίκιο , αυτό είναι το μειονέκτημα του αντιπαραδείγματος . Για απλές συκέ περιπτώσεις ασκήσεων είναι εύκολο να βρεις ποιοι αριθμοί θα δουλέψουν ( συνήθως το 0, 1 , 2 , 3 ,4 κτλπ. ) , αλλά για αυθαίρετες περιπτώσεις όχι τόσο .οχι ρε συ τι να λυσεις με τυχαιους αριθμους!Αυτο ειναι το νοημα του αντιπαραδειγματος.Αν βρεις 2 αριθμους που βγαζουν ιδια συναρτησιακη τιμη σου κατοχυρωνει οτι δεν ειναι 1-1!!Αυτο γινεται γτ ο ορισμος του 1-1 σου λεει για καθε χ1,χ2 επομενως εσυ το αρνεισαι αυτο και θες να δεις αν υπαρχουν 2 τουλαχιστον χ1,χ2 που σου βγαζουν ιδια συναρτησιακη τιμη.Οσο για το πρωτο εκει ειναι η πονηραδα να βγαλεις με τον ορισμο οτι ειναι και στην ενωση f(x1)<f(x2) που ειναι ευκολο ομως γτ αν παρεις χ1 στον ενα κλαδο,χ2 στον αλλο κλαδο ειναι προφανης η διαταξη.
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.965 μηνύματα.

23-07-23

18:30
αυτη η λυση εχει ενα μικρο προβλημα.Αυτο στο οποιο καταληγεις δεν ειναι συστημα!Δηλαδη δεν ισχυουν ταυτοχονα οι 2 εξισωσεις.ειναι ή χ1=χ2 ή χ1+χ2=4.Στην περιπτωση του χ1=χ2 υπαρχει προβλημα!Δεν θα το συνιστουσα!Με αντιπαραδειγμα ειναι πιο καλο.Άλλος τρόπος για την 2 είναι με τον ορισμό:
Για κάθε x1, x2∈R με f(x1)=f(x2) ισχύει:
View attachment 118838
οπότε μπορούμε να βρούμε άπειρα ζεύγη (x1,x2) με διαφορετικά χ, τα οποία δίνουν την ίδια εικόνα.
Αυτόματη ένωση συνεχόμενων μηνυμάτων:
Ναι εχεις ενα δικιο αλλα στα συγκεκριμενα παραδειγματα ειναι αρκετα προφανη τι τιμες θες.Στην μεν συναρτηση με το απολυτη αρκει ουσιαστικα να λυσεις την απολυτο(χ-2)=κατι θετικο και αμεσως θα βρεις τι τιμες θα βαλεις για να σου φτιαξει το αντιπαραδειγμα.....Αν λυσεις πχ την απολυτο(χ-2)=2023 παλι θα δουλεψει.Εννοεί βασικά οτι επιλέγεις τυχαία δύο αριθμούς για το αντιπαράδειγμα . Οτι δεν υπάρχει συστηματικός τρόπος να εντοπίσεις ποιοι δύο αριθμοί θα δουλέψουν . Και έχει δίκιο , αυτό είναι το μειονέκτημα του αντιπαραδείγματος . Για απλές συκέ περιπτώσεις ασκήσεων είναι εύκολο να βρεις ποιοι αριθμοί θα δουλέψουν ( συνήθως το 0, 1 , 2 , 3 ,4 κτλπ. ) , αλλά για αυθαίρετες περιπτώσεις όχι τόσο .
Στην περιπτωση του ριζικου και παλι δοκιμαζεις πχ εκει που μηδενιζει το υποριζο χ=3 και βλεπεις οτι δινει τιμη 1 αρα στον πανω κλαδο αν βαλεις μηδεν παιρνεις ιδια τιμη.Τετοιες ασκησεις ειναι αρκετα ευκολα τα αντιπαραδειγματα.
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 26 ετών, Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 12.152 μηνύματα.

23-07-23

18:42
Το ξέρω , αλλά το κορίτσι είναι της πληροφορικής , μάλλον για αυτό της ξύνισε αυτή η μέθοδοςΝαι εχεις ενα δικιο αλλα στα συγκεκριμενα παραδειγματα ειναι αρκετα προφανη τι τιμες θες.Στην μεν συναρτηση με το απολυτη αρκει ουσιαστικα να λυσεις την απολυτο(χ-2)=κατι θετικο και αμεσως θα βρεις τι τιμες θα βαλεις για να σου φτιαξει το αντιπαραδειγμα.....Αν λυσεις πχ την απολυτο(χ-2)=2023 παλι θα δουλεψει.
Στην περιπτωση του ριζικου και παλι δοκιμαζεις πχ εκει που μηδενιζει το υποριζο χ=3 και βλεπεις οτι δινει τιμη 1 αρα στον πανω κλαδο αν βαλεις μηδεν παιρνεις ιδια τιμη.Τετοιες ασκησεις ειναι αρκετα ευκολα τα αντιπαραδειγματα.
 .
.Πέρα απο την πλάκα όμως , γενικά το αντιπαράδειγμα είναι μια πολύ δυνατή μέθοδος . Ίσως περιορισμένη στην περίπτωση πιο γενικών συναρτήσεων( και επομένως real world συναρτήσεων , aka σήματα )που ούτε τον ορισμό μπορείς να ελέγξεις άμεσα , ούτε να παραγωγίσεις γίνεται ,ούτε να κάνεις εξίσωση εικόνων , οπότε εκεί ναι όντως θες υπολογιστή να ψάξει εξαντλητικά ή να κάνει χρήση κάποιου έξυπνου αλγόριθμου...αλλά πρέπει να δούμε την αξία της μεθόδου σε ένα ευρύτερο πλαίσιο :
Όσα παραδείγματα και να χρησιμοποιήσει κανείς για να αποδείξει την ισχύ μιας πρότασης δεν θα είναι αρκετά ορισμένες φορές ( εκτός εαν έχει να ελέγξει πεπερασμένο αριθμό περιπτώσεων οπότε αποδεικνύει το ζητούμενο εύκολα με εξαντλητικό τρόπο ). Για να λύσει κανείς τα χέρια του σε αυτή την περίπτωση πρέπει να βασιστεί σε κάποια αποδεικτική διαδικασία ευρύτερου βεληνεκούς ( λόγου χάρη μέθοδος της επαγωγής ) . Το αντιπαράδειγμα όμως είναι δυνατό ακριβώς επειδή με ένα και μόνο παράδειγμα μπορείς να αποδείξεις οτι σίγουρα κάτι δεν ισχύει .
@Helen06 εαν σε ενδιαφέρει σε περισσότερο βάθος το που πάει η κουβέντα θα σου πρότεινα να ψάξεις για το γνωστό N vs NP . Είναι ένα πολύ συναρπαστικό και πολύ ενδιαφέρον πρόβλημα που κάθεται μεταξύ μαθηματικών και επιστήμης υπολογιστών .
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.965 μηνύματα.

23-07-23

18:47
Σωστα.Ουσιαστικα με ενα απλο παραδειγμα αποδεικνυεις οτι δεν ισχυει καθολικα ο ορισμος και αρα καιγεται οτι ειναι 1-1 στην προκειμενη περιπτωση.Ηταν 2-3 χρονιες στις πανελληνιες που το αναδεικνυαν αυτο το κομματι του αντιπαραδειγματος κυριως στο πρωτο θεμα.Ομως θεωρηθηκε too much για πρωτο θεμα γτ οι μοναδες θεωρουνται στημενες,τους κραξανε ασχημα και εδω και καμια τριετια το ξαναεβγαλαν.Το ξέρω , αλλά το κορίτσι είναι της πληροφορικής , μάλλον για αυτό της ξύνισε αυτή η μέθοδος.
Πέρα απο την πλάκα όμως , γενικά το αντιπαράδειγμα είναι μια πολύ δυνατή μέθοδος . Ίσως περιορισμένη στην περίπτωση πιο γενικών συναρτήσεων που ούτε τον ορισμό μπορείς να ελέγξεις άμεσα , ούτε να παραγωγίσεις γίνεται , ούτε να κάνεις εξίσωση εικόνων , οπότε εκεί ναι όντως θες υπολογιστή να ψάξει εξαντλητικά ή να κάνει χρήση κάποιου έξυπνου αλγόριθμου...αλλά πρέπει να δούμε την αξία της μεθόδου σε ένα ευρύτερο πλαίσιο :
Όσα παραδείγματα και να χρησιμοποιήσει κανείς για να αποδείξει την ισχύ μιας πρότασης δεν είναι αρκετά ορισμένες φορές ( εκτός εαν έχει να ελέγξει για πεπερασμένο αριθμό περιπτώσεων οπότε το αποδεικνύει εξαντλητικά ). Οπότε εκεί πρέπει να βασιστεί σε κάποια αποδεικτική διαδικασία ευρύτερου βεληνεκούς ( λόγου χάρη μέθοδος της επαγωγής ) . Το αντιπαράδειγμα όμως είναι δυνατό ακριβώς επειδή με ένα και μόνο παράδειγμα μπορείς να αποδείξεις οτι σίγουρα κάτι δεν ισχύει .
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 26 ετών, Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 12.152 μηνύματα.

23-07-23

18:52
Πιστεύω οτι γενικά πρέπει να αφιερωθούν κάποια μαθήματα λίγο στο κομμάτι της λογικής , των αποδείξεων , των επιχειρημάτων κτλπ . Είναι κρίσιμο και βασικό γιατί είτε κάνεις άλγεβρα , είτε λογισμό , είτε γεωμετρία είτε οποιοδήποτε κλάδο των μαθηματικών , οι βασικές αποδεικτικές πρακτικές παραμένουν επί της ουσίας ίδιες . Είναι σαν να λέμε τα θεμέλια των μαθηματικών , όπως τα μαθηματικά αποτελούν τα θεμέλια για άλλες επιστήμες . Και μεταξύ μας τώρα η αλήθεια να λέγεται , ποιο χρήσιμη είναι η λογική σε καθημερινό επίπεδο και στον προγραμματισμό παρά ο λογισμός . Γιατί λογική όλοι θα χρησιμοποιήσουν στην ζωή τους , και ιδίως όσοι ασχοληθούν με υπολογιστές πρέπει να έχουν ένα πιο firm grasp . Απο την άλλη λογισμό , όχι , δεν θα χρησιμοποιήσουν όλοι . Τουλάχιστον όχι άμεσα .Σωστα.Ουσιαστικα με ενα απλο παραδειγμα αποδεικνυεις οτι δεν ισχυει καθολικα ο ορισμος και αρα καιγεται οτι ειναι 1-1 στην προκειμενη περιπτωση.Ηταν 2-3 χρονιες στις πανελληνιες που το αναδεικνυαν αυτο το κομματι του αντιπαραδειγματος κυριως στο πρωτο θεμα.Ομως θεωρηθηκε too much για πρωτο θεμα γτ οι μοναδες θεωρουνται στημενες,τους κραξανε ασχημα και εδω και καμια τριετια το ξαναεβγαλαν.
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.965 μηνύματα.

23-07-23

18:56
Την λογικη δεν την ακουμπανε στο λυκειο γτ ισως φοβουνται οτι επειδη ειναι αφηρημενο ως αντικειμενο θα δυσκολεψει τους μαθητες.Ειναι σαν να πας να μιλησεις για δακτυλιους,σωματα και ισομορφισμους στο λυκειο.Ακομα και ο πιο πορωμενος μαθητης θα κοιταει σαν χανος.Αντιθετα,ο διαφορικος λογισμος χρησιμοποιειται παντου μα παντου στις επιστημες και το κομματι της βελτιστοποιησης συναρτησεων ειναι πολυ διασημο κομματι.Το θεμα βεβαια ειναι οτι ως συνηθως παλι μπαινει το στοιχειο υπερβολης καθως αναζητουνται ασκησεις ακραιες του στυλ απεδειξε οτι υπαρχουν ξ1,ξ2 κτλπ για να ισχυει εκεινο κτλπ με χρηση 20 θμτ και ετσι δεν καταδεικνυεται η χρησιμοτητα του διαφορικου λογισμου.Πιστεύω οτι γενικά πρέπει να αφιερωθούν κάποια μαθήματα λίγο στο κομμάτι της λογικής , των αποδείξεων , των επιχειρημάτων κτλπ . Είναι κρίσιμο και βασικό γιατί είτε κάνεις άλγεβρα , είτε λογισμό , είτε γεωμετρία είτε οποιοδήποτε κλάδο των μαθηματικών , οι βασικές αποδεικτικές πρακτικές παραμένουν επί της ουσίας ίδιες . Είναι σαν να λέμε τα θεμέλια των μαθηματικών , όπως τα μαθηματικά αποτελούν τα θεμέλια για άλλες επιστήμες . Και μεταξύ μας τώρα η αλήθεια να λέγεται , ποιο χρήσιμη είναι η λογική σε καθημερινό επίπεδο και στον προγραμματισμό παρά ο λογισμός . Γιατί λογική όλοι θα χρησιμοποιήσουν στην ζωή τους , και ιδίως όσοι ασχοληθούν με υπολογιστές πρέπει να έχουν ένα πιο firm grasp . Απο την άλλη λογισμό , όχι , δεν θα χρησιμοποιήσουν όλοι . Τουλάχιστον όχι άμεσα .
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 26 ετών, Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 12.152 μηνύματα.

23-07-23

19:16
Είναι όλα θέμα παρουσίασης πιστεύω . Καθημερινά πολύς κόσμος σε υποσυνείδητο επίπεδο κάνει διάφορα μαθηματικά χωρίς να το αντιλαμβάνεται . Άλλωστε τα μαθηματικά σχετίζονται με την σκέψη κάποιου . Οπότε θεωρητικά μπορεί κάποιος που δεν έχει διδαχτεί formally μαθηματικά ποτέ να έχει μαθηματική σκέψη . Άλλοι περισσότερο άλλοι λιγότερο . Δεν λέμε να κάνουν όλη την λογική , αλλά κάποια βασικά στοιχεία θα ήταν χρήσιμα αφενός αλλά και ιδιαίτερα ενδιαφέρον αφετέρου . Άλλωστε και ο λογισμός εαν τον παρακολουθήσει κάποιος σε πανεπιστημιακό επίπεδο , με αυστηρή θεμελίωση , μόνο ευχάριστος όπως στο λύκειο δεν είναι . Κυρίως επειδή αναλώνεις τεράστιο χρόνο και προσπάθεια για να αποδείξεις πράγματα που κατά τα άλλα σου μπορεί να φαίνονται και εντελώς προφανείς . Η ουσία βέβαια δεν είναι να σκοτωθείς για να αποδείξεις το προφανές αλλά να εξασκηθείς στο να έχεις έναν συστηματικό τρόπο σκέψης για την αντιμετώπιση προβλημάτων , προφανή και μη .Την λογικη δεν την ακουμπανε στο λυκειο γτ ισως φοβουνται οτι επειδη ειναι αφηρημενο ως αντικειμενο θα δυσκολεψει τους μαθητες.Ειναι σαν να πας να μιλησεις για δακτυλιους,σωματα και ισομορφισμους στο λυκειο.Ακομα και ο πιο πορωμενος μαθητης θα κοιταει σαν χανος.Αντιθετα,ο διαφορικος λογισμος χρησιμοποιειται παντου μα παντου στις επιστημες και το κομματι της βελτιστοποιησης συναρτησεων ειναι πολυ διασημο κομματι.Το θεμα βεβαια ειναι οτι ως συνηθως παλι μπαινει το στοιχειο υπερβολης καθως αναζητουνται ασκησεις ακραιες του στυλ απεδειξε οτι υπαρχουν ξ1,ξ2 κτλπ για να ισχυει εκεινο κτλπ με χρηση 20 θμτ και ετσι δεν καταδεικνυεται η χρησιμοτητα του διαφορικου λογισμου.
arko
Εκκολαπτόμενο μέλος
Ο Κωνσταντίνος αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 20 ετών και Φοιτητής του τμήματος Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών ΕΜΠ. Έχει γράψει 177 μηνύματα.

23-07-23

19:37
Καταλαβαίνεις ότι δεν είναι ή ότι είναι 1-1 με τη γνωστή τεχνική «με το ματι».Τέλεια σ'ευχαριστώ πάρα πολύ. Και εγώ αυτό έκανα στη δίκλαδη μόνο που μετά δε μπόρεσα να βρω για όλη την F(X). Ωστόσο στο β) πως ξέρω ότι όντως δεν είναι 1-1, πρέπει πριν να ξεκινήσω να τη λύνω να δοκιμάζω αυτό με τους τυχαίους αριθμούς;
Προσωπικά σχεδιάζω μια πρόχειρη γραφική παράσταση όταν γίνεται, αλλιως βλέπεις άμα είναι άρτια.
αλλιώς ματι ή απόδειξη.
Cade
Πολύ δραστήριο μέλος
Ο Cade αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Απόφοιτος λυκείου. Έχει γράψει 872 μηνύματα.

23-07-23

19:47
Μα η περίπτωση x1=x2 είναι τετριμμένη, προφανώς θα υπάρχει στις λύσεις που θα βρούμε και μάλιστα δείχνω ότι δεν είναι μοναδική. Από τη δεύτερη σχέση μπορούμε να βρούμε x1, x2 διαφορετικά με τις ίδιες εικόνες, άρα τελειώσαμε (όπως άλλωστε αποδεικνύουν οι αντίστροφες συναπαγωγες). Συμφωνείς με τα παραπάνω; Δεν καταλαβαίνω που είναι το πρόβλημα.αυτη η λυση εχει ενα μικρο προβλημα.Αυτο στο οποιο καταληγεις δεν ειναι συστημα!Δηλαδη δεν ισχυουν ταυτοχονα οι 2 εξισωσεις.ειναι ή χ1=χ2 ή χ1+χ2=4.Στην περιπτωση του χ1=χ2 υπαρχει προβλημα!Δεν θα το συνιστουσα!Με αντιπαραδειγμα ειναι πιο καλο.
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.965 μηνύματα.

24-07-23

02:55
Γτ τετριμμενο οτι χ1=χ2 αφου την εξισωση λυνεις!Εμενα ο προβληματισμος μου ειναι στο ή.Το ή σημαινει οτι μπορει να ισχυει ειτε η μια σχεση ειτε η αλλη σχεση ειτε και οι δυο!Και αν ισχυει η μια σχεση χ1=χ2 τι γινεται σε αυτη την περιπτωση?Το θεωρω επισφαλη τροπο αποδειξης.Δεν ειναι απολυτα λαθος αλλα πολυ καλυτερο να το παει καποιος με αντιπαραδειγμα και να μην το μπλεξει με γενικοτητες που βαζουν προβληματα.Μα η περίπτωση x1=x2 είναι τετριμμένη, προφανώς θα υπάρχει στις λύσεις που θα βρούμε και μάλιστα δείχνω ότι δεν είναι μοναδική. Από τη δεύτερη σχέση μπορούμε να βρούμε x1, x2 διαφορετικά με τις ίδιες εικόνες, άρα τελειώσαμε (όπως άλλωστε αποδεικνύουν οι αντίστροφες συναπαγωγες). Συμφωνείς με τα παραπάνω; Δεν καταλαβαίνω που είναι το πρόβλημα.
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 26 ετών, Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 12.152 μηνύματα.

24-07-23

08:09
Προφανώς για όλα τα x1 = x2 θα είναι f(x1) = f(x2) βάσει του ορισμού της συνάρτησης . Η απόδειξη του Cade βασίζεται στο γεγονός ότι ξεκινάει με την παραδοχή ότι f(x1) = f(x2) και καταλήγει στο συμπέρασμα ότι η σχέση μεταξύ των x1 και x2 είναι :Γτ τετριμμενο οτι χ1=χ2 αφου την εξισωση λυνεις!Εμενα ο προβληματισμος μου ειναι στο ή.Το ή σημαινει οτι μπορει να ισχυει ειτε η μια σχεση ειτε η αλλη σχεση ειτε και οι δυο!Και αν ισχυει η μια σχεση χ1=χ2 τι γινεται σε αυτη την περιπτωση?Το θεωρω επισφαλη τροπο αποδειξης.Δεν ειναι απολυτα λαθος αλλα πολυ καλυτερο να το παει καποιος με αντιπαραδειγμα και να μην το μπλεξει με γενικοτητες που βαζουν προβληματα.
x1 = x2 ή x1+x2 = 4
Οπότε έχεις λύσεις που ισχύει απλώς x1 = x2 , που είναι οι τετριμμένες και δεν σε ενδιαφέρουν γιατί υπάρχουν για όλες τις συναρτήσεις είτε είναι 1-1 είτε όχι . Υπάρχει μια λύση x1 = x2 = 2 για την οποία ισχύουν ταυτόχρονα και οι δύο σχέσεις που πάλι δεν σε ενδιαφέρει γιατί ανήκει και αυτή στις τετριμμένες λύσεις...και τέλος υπάρχουν και λύσεις που ικανοποιούν μόνο την εξίσωση :
x1 + x2 = 4
Οπότε εάν πάρεις π.χ. :
x1 = 1 και x2 = 3 , βρίσκεις ότι f(x1) = f(x2) . Επί της ουσίας ο τρόπος του Cade είναι πιο ισχυρή απόδειξη του ζητούμενου καθώς σε αντίθεση με το αντιπαράδειγμα , δεν αποδεικνύει απλώς ότι η f είναι 1-1 αλλά και για ποια x1 != x2 ισχύει f(x1) = f(x2) .
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.965 μηνύματα.

26-07-23

13:56
Tεσπα τωρα που το ξανασκεφτομαι εχετε δικιο.Ουσιαστικα ειναι σαν να λυνεις μια εξισωση απολυτοχ=θ που ειναι ειτε θ ειτε -θ το χ κατι αναλογο και εδω.Βρηκες χ1,χ2 τα οποια ειναι απειρα σε αριθμο οπως αποδεικνευται απο χ1+χ2=4 που σπαει το 1-1.Τεσπα,παντως συνηθης τακτικη σε αυτα τα θεματα ειναι το αντιπαραδειγμα οποτε να μην λαβουν αυτη τη λυση οι υποψηφιοι ως υποδειγμα.Προφανώς για όλα τα x1 = x2 θα είναι f(x1) = f(x2) βάσει του ορισμού της συνάρτησης . Η απόδειξη του Cade βασίζεται στο γεγονός ότι ξεκινάει με την παραδοχή ότι f(x1) = f(x2) και καταλήγει στο συμπέρασμα ότι η σχέση μεταξύ των x1 και x2 είναι :
x1 = x2 ή x1+x2 = 4
Οπότε έχεις λύσεις που ισχύει απλώς x1 = x2 , που είναι οι τετριμμένες και δεν σε ενδιαφέρουν γιατί υπάρχουν για όλες τις συναρτήσεις είτε είναι 1-1 είτε όχι . Υπάρχει μια λύση x1 = x2 = 2 για την οποία ισχύουν ταυτόχρονα και οι δύο σχέσεις που πάλι δεν σε ενδιαφέρει γιατί ανήκει και αυτή στις τετριμμένες λύσεις...και τέλος υπάρχουν και λύσεις που ικανοποιούν μόνο την εξίσωση :
x1 + x2 = 4
Οπότε εάν πάρεις π.χ. :
x1 = 1 και x2 = 3 , βρίσκεις ότι f(x1) = f(x2) . Επί της ουσίας ο τρόπος του Cade είναι πιο ισχυρή απόδειξη του ζητούμενου καθώς σε αντίθεση με το αντιπαράδειγμα , δεν αποδεικνύει απλώς ότι η f είναι 1-1 αλλά και για ποια x1 != x2 ισχύει f(x1) = f(x2) .
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 1 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 60 μέλη διάβασαν αυτό το θέμα:
- sugar123
- Corfu kitty
- phleidhs
- Mary06
- suaimhneas
- carnage
- eukleidhs1821
- iiTzArismaltor_
- Hased Babis
- ggl
- ειδήμων
- Helen06
- panagiotis12
- Joji
- spring day
- Ameliak
- pannnos1992
- Wonderkid
- arapakos
- Lathy
- Kolptsres
- arko
- jimis2001
- george777
- suuuuiiii
- Frozensun
- Panagiotis849
- constansn
- flaura
- Ultimate_duck87
- GeorgePap2003
- Unboxholics
- Magigi
- Νικολινα
- Maynard
- Giannis_19
- angies
- stam23
- a namaves
- P.Dam.
- dmav
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki



