eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3,928 μηνύματα.

06-10-20

19:07
ειδες βρε τελικα οτι και τα μαθηματικα εχουν φαση και δεν ειναι μονο τα κομπιουτερ και οι μηχανες οπως τονιζεις συνεχεια?Η καλύτερη απόδειξη για εμένα πιστεύω είναι του Βασίλη γιατί 1ον) είναι η απλούστερη, 2ον)Μαθηματικώς μιλώντας είναι η πιο αναλυτική , και 3ον)χρησιμοποιεί την ανισότητα Cauchy-Schwarz, βλέποντας ως διανύσματα τα χ1= <α,b> & χ2= <sinx,cosx>.
Η απόδειξη μπορεί να γίνει και με χρήση μιγαδικών, αν εκφραστούν τα sinx και cosx ως μιγαδικά εκθετικά. Συγκεκριμένα καταλήγουμε σε μια έκφραση της μορφής :
αsinx+bcosx = cos(x-θ)*√α²+b² <= √α²+b² ,εφόσον cos(χ-θ)<=1
Όπου θ =
{atan(α/β) ,εαν α>0 & β>0
π-atan(-α/β) , εαν α>0 & β<0
-atan(-α/β), εαν α<0 & β>0
-π+atan(α/β) , εαν α<0 & α<0 }
Όπως και πριν εαν x = 2κπ+θ, για κ=0,1,2,...τότε ισχύει η ισότητα.
Για παράδειγμα εαν κ = 0, α>0 ^ b>0 => χ= θ =atan(α/β) => x-θ = 0 => cos(χ-θ) = 1 => αsinx+bcosx = √α²+b²
Η απλούστερη λύση όλων και μάλλον αυτό που θα αρκούσε σε μια εξέταση, αλλά η λιγότερο ας πούμε "εντυπωσιακή" είναι να σκεφτεί κανείς στο αρχικό πρόβλημα :
sinx+cosx = 2 , οτι το cosx προπορεύεται του sinx κατά π/2 . Κάνοντας το γράφημα των δυο συναρτήσεων λοιπόν για το διάστημα [0,2π] (ως περιοδικές συναρτήσεις) είναι φανερό οτι δεν παίρνουν ποτέ στο ίδιο σημείο την τιμή 1,σε όλο το R .
Διασκεδαστικό πρόβλημα θα έλεγα, από την άποψη οτι ώθησε σε αποδείξεις της γενίκευση του.
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11,341 μηνύματα.

06-10-20

19:48
ειδες βρε τελικα οτι και τα μαθηματικα εχουν φαση και δεν ειναι μονο τα κομπιουτερ και οι μηχανες οπως τονιζεις συνεχεια?
Δεν θυμάμαι να έχω αναφέρει ποτέ οτι τα μαθηματικά είναι οι υπολογιστές και οι μηχανές.
Τώρα εαν εχω πει οτι η θεωρητική πληροφορική στην ουσία είναι μαθηματικά ή οτι οι υπολογιστές και οι μηχανές όσον αφορά στο λειτουργικό τους κομμάτι είναι μαθηματικές μηχανές ίσως
 . Εκτός βέβαια εαν κάποιος δεν λογαριάζει τα υπολογιστικά μαθηματικά... ως μαθηματικά.
. Εκτός βέβαια εαν κάποιος δεν λογαριάζει τα υπολογιστικά μαθηματικά... ως μαθηματικά.
06-10-20

19:56
Αφού λέμε αποδείξεις για την γενικη ανισοτητα ας πω κιεγώ τη δική μου όπως τη σκέφτηκα. Ορίζω γωνία y τέτοια ώστε ημy/συνy= β/α ( α,β>0)
Έχουμε αημχ + βσυνχ =(συνyημχ + ημyσυνχ) * α/συνy => αημχ + βσυνχ= ημ(x+y) *α/συνy( σχεση 1).Αντικαθιστώ στη σχέση ημ^2y+ συν^2y= 1 και παίρνω (β/α * συνy)^2 + συνy^2 =1 => (συνy)^2(α^2 + β^2)/α^2= 1 =>συν^2y = α^2/(α^2 + β^2). Άρα συνy= α/ριζα(α^2 + β^2) και ημy = β/ριζα(α^2 + β^2). Αντικαθιστώ στην σχέση 1 και παίρνω: αημχ + βσυνχ = ημ(χ + y) * α/(α/ριζα(α^2+β^2)) = ριζα(α^2 + β^2) * ημ( χ + y) με y= arctan β/α. Είναι προφανές πλέον ότι η μέγιστη τιμή που παίρνει η παράσταση ριζα(α^2 + β^2) *ημ( χ + y) είναι η ρίζα(α^2 + β^2).Μπορώ βέβαια να δείξω το ίδιο και αν πάρω συνημίτονο και ημίτονο αρνητικά μόνο που θα προκύψει η ίδια παράσταση με ενα - μπροστά. Αν και μπορώ απλά να θεωρήσω τα ημy και συνy θετικά απο την αρχή. Φαντάζομαι αυτή είναι η "απευθείας" απόδειξη που ανέφερε ο Μάρκος Βασίλης;
Έχουμε αημχ + βσυνχ =(συνyημχ + ημyσυνχ) * α/συνy => αημχ + βσυνχ= ημ(x+y) *α/συνy( σχεση 1).Αντικαθιστώ στη σχέση ημ^2y+ συν^2y= 1 και παίρνω (β/α * συνy)^2 + συνy^2 =1 => (συνy)^2(α^2 + β^2)/α^2= 1 =>συν^2y = α^2/(α^2 + β^2). Άρα συνy= α/ριζα(α^2 + β^2) και ημy = β/ριζα(α^2 + β^2). Αντικαθιστώ στην σχέση 1 και παίρνω: αημχ + βσυνχ = ημ(χ + y) * α/(α/ριζα(α^2+β^2)) = ριζα(α^2 + β^2) * ημ( χ + y) με y= arctan β/α. Είναι προφανές πλέον ότι η μέγιστη τιμή που παίρνει η παράσταση ριζα(α^2 + β^2) *ημ( χ + y) είναι η ρίζα(α^2 + β^2).Μπορώ βέβαια να δείξω το ίδιο και αν πάρω συνημίτονο και ημίτονο αρνητικά μόνο που θα προκύψει η ίδια παράσταση με ενα - μπροστά. Αν και μπορώ απλά να θεωρήσω τα ημy και συνy θετικά απο την αρχή. Φαντάζομαι αυτή είναι η "απευθείας" απόδειξη που ανέφερε ο Μάρκος Βασίλης;
asdfqwerty
Πολύ δραστήριο μέλος
Ο asdfqwerty αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Φοιτητής του τμήματος Πληροφορικής & Τηλεπικοινωνιών ΕΚΠΑ. Έχει γράψει 1,347 μηνύματα.

06-10-20

20:31
αν θυμαμαι καλα γιατι εχει περασει αρκετος καιρος η ανισοτητα |a b|<=|a||b| με α , β διανυσματαΝαι, κι αυτό υπάρχουν αρκετοί τρόποι για να το δεις - π.χ. με παραγώγιση και 2-3 κιλά πράξεις ή με απευθείας απόδειξη της παραπάνω ανισότητας - ή πιο απλά, από την ανισότητα Cauchy-Schwarz για u=(a,b) και v=(sinx,cosx):
,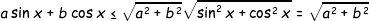
με το = να επιτυγχάνεται αν και μόνο αν τα u,v είναι γραμμικώς εξαρτημένα, δηλαδή όταν:
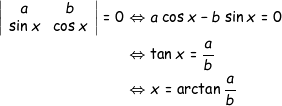
υπαρχει στο σχολικο ως εφαρμογη
Μάρκος Βασίλης
Πολύ δραστήριο μέλος
Ο Βασίλης αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 28 ετών, Διδακτορικός και μας γράφει από Καισαριανή (Αττική). Έχει γράψει 1,871 μηνύματα.

06-10-20

20:45
αν θυμαμαι καλα γιατι εχει περασει αρκετος καιρος η ανισοτητα |a b|<=|a||b| με α , β διανυσματα
υπαρχει στο σχολικο ως εφαρμογη
Ναι, αλλά δεν τη λένε με το όνομά της. Αλλά για δύο διανύσματα δύο διαστάσεων βγαίνει εύκολα με άλγεβρα της Α' λυκείου.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 4 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 74 μέλη διάβασαν αυτό το θέμα:
- Mary06
- ggl
- Mariaathens
- AlexK9
- Teorer
- Maynard
- T C
- Κορώνα
- eukleidhs1821
- Unboxholics
- Μάρκος Βασίλης
- Alexandros973
- Κλημεντίνη
- Nefh_
- jimis2001
- nucomer
- Scandal
- harry akritas
- Thanos_D
- Stroka
- Athens2002
- leo41
- tsiobieman
- Monster Hunter
- Bgpanos
- American Economist
- TonyMontanaEse
- Cortes
- igeorgeoikonomo
- Unseen skygge
- PanosBat
- the purge
- BioChemical
- Meow
- Λαμπρινηη
- Vold
- J.Cameron
- Panagiotis849
- Johnman97
- Memetchi
- Drglitterstar
- kiyoshi
- SlimShady
- MarcoReus
- nicole1982
- Φινεύς
- Βλα
- Αλκης Κ.
- Kostakis45
- giannhs2001
-
Φορτώνει...
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki

