Κορώνα
Νεοφερμένος
Η Κορώνα αυτή τη στιγμή δεν είναι συνδεδεμένη. Είναι 23 ετών. Έχει γράψει 45 μηνύματα.

05-10-20

02:08
Στην περίπτωση που καταλήξουμε σε εξίσωση της μορφής: ημχ+συνχ=2 τι μπορούμε να κάνουμε για να την λύσουμε;
The Mountain
Πολύ δραστήριο μέλος
Ο The Mountain αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Φοιτητής. Έχει γράψει 944 μηνύματα.

05-10-20

02:18
Τίποτα γιατί δεν έχει λύση. Σκέψου τι τιμές παίρνουν οι cos(x) και sin(x) και που τις παίρνουν για να το διαπιστώσεις. Αν δεν το χεις ξαναρωτάς.
γιαννης_00
Επιφανές μέλος
Ο γιαννης_00 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 24 ετών, Φοιτητής του τμήματος Πρόγραμμα Ιερατικών Σπουδών και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 12,666 μηνύματα.

05-10-20

03:45
Στην περίπτωση που καταλήξουμε σε εξίσωση της μορφής: ημχ+συνχ=2 τι μπορούμε να κάνουμε για να την λύσουμε;
Αν σωστα εχεις καταληξει εκει δεν υπαρχει λυση με το χ να ανήκει στο R οπως σωστα αναφερει ο the mountain .
Λυση υπαρχει στο πεδιο των μιγαδικων αλλα αυτο διδασκεται σε καποιες σχολες στο πανεπιστημιο.
Στην περίπτωση που καταλήξουμε σε εξίσωση της μορφής: ημχ+συνχ=2 τι μπορούμε να κάνουμε για να την λύσουμε;
Κορωνα βλεποντας παλι την απαντηση που σου εδωσα ειναι μεν προφανης και σωστη αλλα μαθηματικως δεν στεκει.
Η αποδεκτη μαθηματικα αποδειξη θα ηταν να στηριχθούμε σε κατι μαθηματικως αποδεκτο πχ το πεδιο τιμων του
ημχ ή του συνχ το οποιο ειναι μεταξυ -1 εως 1. Αν σου ειναι σημαντικη αυτη η ασκηση πες να το προσπαθησω.
Εμεις στην φυσικη χρησιμοποιουμε συχνα τετοια βολικα προφανη συμπερασματα αλλα εκει οι μαθηματικοι θυμωνουν.
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3,928 μηνύματα.

05-10-20

14:44
Η εξισωση εχει λυση αν λυνεται το συστημα ημχ=1 και συνχ=1 διοτι ημχ<=1 και συνχ<=1 ημχ=1 λυνεται για χ=2κπ+π/2 και συν(2κπ+π/2)=συνπ/2=0 αρα το συστημα ειναι αδυνατο.αρα η εξισωση ειναι αδυνατηΣτην περίπτωση που καταλήξουμε σε εξίσωση της μορφής: ημχ+συνχ=2 τι μπορούμε να κάνουμε για να την λύσουμε;
Κορώνα
Νεοφερμένος
Η Κορώνα αυτή τη στιγμή δεν είναι συνδεδεμένη. Είναι 23 ετών. Έχει γράψει 45 μηνύματα.

05-10-20

19:49
Σας ευχαριστώ για τις απαντήσεις όλους απλά έχει τύχει να λύνω γενικές ασκήσεις και να φτάνω σε αυτή την εξίσωση ενώ όλα είναι σωστά
γιαννης_00
Επιφανές μέλος
Ο γιαννης_00 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 24 ετών, Φοιτητής του τμήματος Πρόγραμμα Ιερατικών Σπουδών και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 12,666 μηνύματα.

05-10-20

19:55
Σας ευχαριστώ για τις απαντήσεις όλους απλά έχει τύχει να λύνω γενικές ασκήσεις και να φτάνω σε αυτή την εξίσωση ενώ όλα είναι σωστά
Α καταλαβα... οχι η ασκηση αυτη δεν μπορει να ειναι υποψηφιο θεμα . Δεν ξερω ποσο κουραστικες για να φτασεις εκει αλλα αν σου γραψω την συνεχεια θα δεις οτι ειναι κουραστικο ,δυσκολο και ανουσιο θεμα.
Μάρκος Βασίλης
Πολύ δραστήριο μέλος
Ο Βασίλης αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 28 ετών, Διδακτορικός και μας γράφει από Καισαριανή (Αττική). Έχει γράψει 1,871 μηνύματα.

05-10-20

23:16
Α καταλαβα... οχι η ασκηση αυτη δεν μπορει να ειναι υποψηφιο θεμα . Δεν ξερω ποσο κουραστικες για να φτασεις εκει αλλα αν σου γραψω την συνεχεια θα δεις οτι ειναι κουραστικο ,δυσκολο και ανουσιο θεμα.
Καθόλου δύσκολο θέμα δεν είναι, είναι η αλήθεια. Αρχικά, δεδομένου ότι
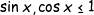
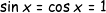
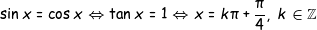
Όμως:
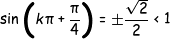
Άρα δεν έχουμε λύση.
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3,928 μηνύματα.

06-10-20

00:24
και ετσι οπως το κανω εγω το ιδιο ειναι,αλλα και αυτο καλη λυση ειναιΚαθόλου δύσκολο θέμα δεν είναι, είναι η αλήθεια. Αρχικά, δεδομένου ότιέπεται άμεσα ότι για να ισχύει η παραπάνω πρέπει να έχουμε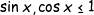 . Ωστόσο:
. Ωστόσο: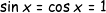
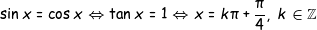
Όμως:
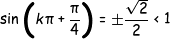
Άρα δεν έχουμε λύση.

06-10-20

09:38
Fun fact: Μια παράσταση της μορφής αημχ + βσυνχ πιάνει μέγιστη τιμή την sqrt(α^2 + β^2). Η συγκεκριμένη πιάνει την sqrt2. Η 3ημχ + 4συνχ για παράδειγμα πιάνει μέγιστη τιμή την 5.
Μάρκος Βασίλης
Πολύ δραστήριο μέλος
Ο Βασίλης αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 28 ετών, Διδακτορικός και μας γράφει από Καισαριανή (Αττική). Έχει γράψει 1,871 μηνύματα.

06-10-20

10:04
Fun fact: Μια παράσταση της μορφής αημχ + βσυνχ πιάνει μέγιστη τιμή την sqrt(α^2 + β^2). Η συγκεκριμένη πιάνει την sqrt2. Η 3ημχ + 4συνχ για παράδειγμα πιάνει μέγιστη τιμή την 5.
Ναι, κι αυτό υπάρχουν αρκετοί τρόποι για να το δεις - π.χ. με παραγώγιση και 2-3 κιλά πράξεις ή με απευθείας απόδειξη της παραπάνω ανισότητας - ή πιο απλά, από την ανισότητα Cauchy-Schwarz για u=(a,b) και v=(sinx,cosx):
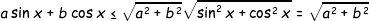
με το = να επιτυγχάνεται αν και μόνο αν τα u,v είναι γραμμικώς εξαρτημένα, δηλαδή όταν:
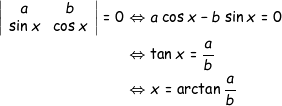
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3,928 μηνύματα.

06-10-20

12:37
Απο περιεργεια φ(χ)=sinx+cosx φ'(χ)=cosx-sinx φ'(χ)=0 συνεπαγεται χ=κπ+π/4 φ''(χ)=-sinx-cosx=
-(sinx+cosx) .Αν κ αρτιος φ''(κπ+π/4)=-ριζα2<0 αρα εχει μεγιστο το ριζα2/2+ριζα2/2=ριζα2.
Αν κ περιττος φ''(κπ+π/4)=-(-ριζα2)=ριζα2>0 αρα εχει ελαχιστο το -ριζα2.
αυτο δεν ξερω σε επιπεδο γ λυκειου αν υπαρχει θεωρια ή αποδειξη.αποδεικνυεται ως εξης.φ''(χ0)=lim(f'(x)-f'(x0)/x-x0) αν το οριο αυτο ειναι θετικο κοντα στο χ0 σημαινει το κλασμα θετικο.Για τα χ δεξιοτερα του χ0 f'(x)>f'(x0) για τα αριστεροτερα f'(x)<f'(x0) ομως f'(x0)=0 αρα σε μια περιοχη αριστερα του χ0 γν.φθινουσα,δεξιοτερα γν.αυξουσα αρα τοπικο ελαχιστο.
Επαναλαμβανω δεν ξερω αν αυτο ειναι θεωρια ή οχι απλα το αναφερω για να μην μπερδευτει καποιος πως πηρα στην παραπανω ασκηση αυτο το συμπερασμα
Eπισης για τους πανεπιστημιακους αποδεικνυεται και μεσω πολυωνυμου taylor δευτερης ταξης
-(sinx+cosx) .Αν κ αρτιος φ''(κπ+π/4)=-ριζα2<0 αρα εχει μεγιστο το ριζα2/2+ριζα2/2=ριζα2.
Αν κ περιττος φ''(κπ+π/4)=-(-ριζα2)=ριζα2>0 αρα εχει ελαχιστο το -ριζα2.
Αυτόματη ένωση συνεχόμενων μηνυμάτων:
αυτο δεν ξερω σε επιπεδο γ λυκειου αν υπαρχει θεωρια ή αποδειξη.αποδεικνυεται ως εξης.φ''(χ0)=lim(f'(x)-f'(x0)/x-x0) αν το οριο αυτο ειναι θετικο κοντα στο χ0 σημαινει το κλασμα θετικο.Για τα χ δεξιοτερα του χ0 f'(x)>f'(x0) για τα αριστεροτερα f'(x)<f'(x0) ομως f'(x0)=0 αρα σε μια περιοχη αριστερα του χ0 γν.φθινουσα,δεξιοτερα γν.αυξουσα αρα τοπικο ελαχιστο.
Επαναλαμβανω δεν ξερω αν αυτο ειναι θεωρια ή οχι απλα το αναφερω για να μην μπερδευτει καποιος πως πηρα στην παραπανω ασκηση αυτο το συμπερασμα
Eπισης για τους πανεπιστημιακους αποδεικνυεται και μεσω πολυωνυμου taylor δευτερης ταξης
asdfqwerty
Πολύ δραστήριο μέλος
Ο asdfqwerty αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Φοιτητής του τμήματος Πληροφορικής & Τηλεπικοινωνιών ΕΚΠΑ. Έχει γράψει 1,347 μηνύματα.

06-10-20

14:07
Ναι, κι αυτό υπάρχουν αρκετοί τρόποι για να το δεις - π.χ. με παραγώγιση και 2-3 κιλά πράξεις ή με απευθείας απόδειξη της παραπάνω ανισότητας - ή πιο απλά, από την ανισότητα Cauchy-Schwarz για u=(a,b) και v=(sinx,cosx):
,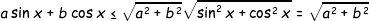
με το = να επιτυγχάνεται αν και μόνο αν τα u,v είναι γραμμικώς εξαρτημένα, δηλαδή όταν:
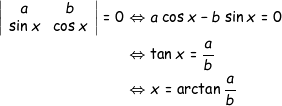
μπορεις να μελετησεις την συγκεριμενη συναρτηση στο [0,2π] αφου ειναι περιοδικη με περιοδο με 2πΑπο περιεργεια φ(χ)=sinx+cosx φ'(χ)=cosx-sinx φ'(χ)=0 συνεπαγεται χ=κπ+π/4 φ''(χ)=-sinx-cosx=
-(sinx+cosx) .Αν κ αρτιος φ''(κπ+π/4)=-ριζα2<0 αρα εχει μεγιστο το ριζα2/2+ριζα2/2=ριζα2.
Αν κ περιττος φ''(κπ+π/4)=-(-ριζα2)=ριζα2>0 αρα εχει ελαχιστο το -ριζα2.
Αυτόματη ένωση συνεχόμενων μηνυμάτων:
αυτο δεν ξερω σε επιπεδο γ λυκειου αν υπαρχει θεωρια ή αποδειξη.αποδεικνυεται ως εξης.φ''(χ0)=lim(f'(x)-f'(x0)/x-x0) αν το οριο αυτο ειναι θετικο κοντα στο χ0 σημαινει το κλασμα θετικο.Για τα χ δεξιοτερα του χ0 f'(x)>f'(x0) για τα αριστεροτερα f'(x)<f'(x0) ομως f'(x0)=0 αρα σε μια περιοχη αριστερα του χ0 γν.φθινουσα,δεξιοτερα γν.αυξουσα αρα τοπικο ελαχιστο.
Επαναλαμβανω δεν ξερω αν αυτο ειναι θεωρια ή οχι απλα το αναφερω για να μην μπερδευτει καποιος πως πηρα στην παραπανω ασκηση αυτο το συμπερασμα
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3,928 μηνύματα.

06-10-20

14:11
σωστος γτ θα εχει την ιδια συμπεριφορα παντου αν την μελετησεις σε αυτο το διαστημα οντας περιοδικη.βεβαια πρωτα θα πρεπει να αποδειξεις οτι ειναι περιοδικη με περιοδο 2π γτ μπορει καποιος να σου πει δεν ξερω δειχτο.μπορεις να μελετησεις την συγκεριμενη συναρτηση στο [0,2π] αφου ειναι περιοδικη με περιοδο με 2π
asdfqwerty
Πολύ δραστήριο μέλος
Ο asdfqwerty αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Φοιτητής του τμήματος Πληροφορικής & Τηλεπικοινωνιών ΕΚΠΑ. Έχει γράψει 1,347 μηνύματα.

06-10-20

14:22
ε απλο ειναι να βγει αλλα ενταξει σε ενα επισημο κειμενο θα ηθελε αποδειξη αλλα δεν υπαρχει περιπτωση να τυχει σε εξετασεις-πανελληνιες κατι τετοιοσωστος γτ θα εχει την ιδια συμπεριφορα παντου αν την μελετησεις σε αυτο το διαστημα οντας περιοδικη.βεβαια πρωτα θα πρεπει να αποδειξεις οτι ειναι περιοδικη με περιοδο 2π γτ μπορει καποιος να σου πει δεν ξερω δειχτο
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3,928 μηνύματα.

06-10-20

14:45
H αποδειξη ειναι.Η περιοδος ειναι 2π διοτι φ(χ+2π)=φ(χ-2π)=φ(χ) και χ+2π,χ-2π ανηκου στο πεδιο ορισμου.Καλο ειναι ολα τα παιδια να ειναι λιγο ψιλιασμενα και να μαθαινουν σε βαθος τα παντα διοτι σε πανελλαδικες εστι θα χτυπησουνε μεγαλο βαθμο,αλλα οχι μονο σε πανελλαδικες και γενικοτερα.Το βαθος και η ευρυτητα σκεψης σε παει μπροστα

06-10-20

14:51
Ένας άλλος τρόπος να το δεις είναι να γράψεις το ημχ + συνχ ως ριζα2*ημ(χ + π/4) με βάση την ταυτοτητα ημ(α + β) = ημασυνβ + συναημβ. Έτσι προκύπτει και η περιοδικότητα αλλά και μια πολύ πιο βολική μορφή για την επίλυση εξισώσεων
Μάρκος Βασίλης
Πολύ δραστήριο μέλος
Ο Βασίλης αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 28 ετών, Διδακτορικός και μας γράφει από Καισαριανή (Αττική). Έχει γράψει 1,871 μηνύματα.

06-10-20

15:24
Απο περιεργεια φ(χ)=sinx+cosx φ'(χ)=cosx-sinx φ'(χ)=0 συνεπαγεται χ=κπ+π/4 φ''(χ)=-sinx-cosx=
-(sinx+cosx) .Αν κ αρτιος φ''(κπ+π/4)=-ριζα2<0 αρα εχει μεγιστο το ριζα2/2+ριζα2/2=ριζα2.
Αν κ περιττος φ''(κπ+π/4)=-(-ριζα2)=ριζα2>0 αρα εχει ελαχιστο το -ριζα2.
Αυτόματη ένωση συνεχόμενων μηνυμάτων:
αυτο δεν ξερω σε επιπεδο γ λυκειου αν υπαρχει θεωρια ή αποδειξη.αποδεικνυεται ως εξης.φ''(χ0)=lim(f'(x)-f'(x0)/x-x0) αν το οριο αυτο ειναι θετικο κοντα στο χ0 σημαινει το κλασμα θετικο.Για τα χ δεξιοτερα του χ0 f'(x)>f'(x0) για τα αριστεροτερα f'(x)<f'(x0) ομως f'(x0)=0 αρα σε μια περιοχη αριστερα του χ0 γν.φθινουσα,δεξιοτερα γν.αυξουσα αρα τοπικο ελαχιστο.
Επαναλαμβανω δεν ξερω αν αυτο ειναι θεωρια ή οχι απλα το αναφερω για να μην μπερδευτει καποιος πως πηρα στην παραπανω ασκηση αυτο το συμπερασμα
Για το όριο είναι εντός το συμπέρασμα της τοπικής συμπεριφοράς - ότι η συνάρτηση έχει τοπικά το ίδιο πρόσημο με το όριό της εκεί.
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3,928 μηνύματα.

06-10-20

15:37
ωραια.το κριτηριο της δευτερης παραγωγου δεν ξερω αν ειναι.Για το όριο είναι εντός το συμπέρασμα της τοπικής συμπεριφοράς - ότι η συνάρτηση έχει τοπικά το ίδιο πρόσημο με το όριό της εκεί.
Μάρκος Βασίλης
Πολύ δραστήριο μέλος
Ο Βασίλης αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 28 ετών, Διδακτορικός και μας γράφει από Καισαριανή (Αττική). Έχει γράψει 1,871 μηνύματα.

06-10-20

15:37
ωραια.το κριτηριο της δευτερης παραγωγου δεν ξερω αν ειναι.
Εκτός, γενικά, αλλά εντός βιβλίου - γενικής παιδείας.
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11,341 μηνύματα.

06-10-20

19:05
Ναι, κι αυτό υπάρχουν αρκετοί τρόποι για να το δεις - π.χ. με παραγώγιση και 2-3 κιλά πράξεις ή με απευθείας απόδειξη της παραπάνω ανισότητας - ή πιο απλά, από την ανισότητα Cauchy-Schwarz για u=(a,b) και v=(sinx,cosx):
,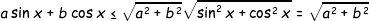
με το = να επιτυγχάνεται αν και μόνο αν τα u,v είναι γραμμικώς εξαρτημένα, δηλαδή όταν:
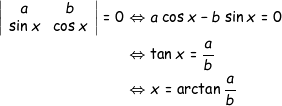
Η καλύτερη απόδειξη για εμένα πιστεύω είναι του Βασίλη γιατί 1ον) είναι η απλούστερη, 2ον)Μαθηματικώς μιλώντας είναι η πιο αναλυτική , και 3ον)χρησιμοποιεί την ανισότητα Cauchy-Schwarz, βλέποντας ως διανύσματα τα χ1= <α,b> & χ2= <sinx,cosx>.
Η απόδειξη μπορεί να γίνει και με χρήση μιγαδικών, αν εκφραστούν τα sinx και cosx ως μιγαδικά εκθετικά. Συγκεκριμένα καταλήγουμε σε μια έκφραση της μορφής :
αsinx+bcosx = cos(x-θ)√(α²+b²) <= √(α²+b²) ,εφόσον cos(χ-θ)<=1
Όπου θ =
{atan(α/β) ,εαν α>0 & β>0
π-atan(-α/β) , εαν α>0 & β<0
-atan(-α/β), εαν α<0 & β>0
-π+atan(α/β) , εαν α<0 & α<0 }
Όπως και πριν εαν x = 2κπ+θ, για κ=0,1,2,...τότε ισχύει η ισότητα.
Για παράδειγμα εαν κ = 0, α>0 ^ b>0 =>
χ= θ =atan(α/β) =>
x-θ = 0 => cos(χ-θ) = 1 =>
αsinx+bcosx = √(α²+b²)
Η απλούστερη λύση όλων και μάλλον αυτό που θα αρκούσε σε μια εξέταση, αλλά η λιγότερο ας πούμε "εντυπωσιακή" είναι να σκεφτεί κανείς στο αρχικό πρόβλημα :
sinx+cosx = 2 , οτι το cosx προπορεύεται του sinx κατά π/2 . Κάνοντας το γράφημα των δυο συναρτήσεων λοιπόν για το διάστημα [0,2π] (ως περιοδικές συναρτήσεις) είναι φανερό οτι δεν παίρνουν ποτέ στο ίδιο σημείο την τιμή 1,σε όλο το R .
Διασκεδαστικό πρόβλημα θα έλεγα, από την άποψη οτι ώθησε σε αποδείξεις της γενίκευσης του.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 2 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 74 μέλη διάβασαν αυτό το θέμα:
- Mary06
- ggl
- Mariaathens
- AlexK9
- Teorer
- Maynard
- T C
- Κορώνα
- eukleidhs1821
- Unboxholics
- Μάρκος Βασίλης
- Alexandros973
- Κλημεντίνη
- Nefh_
- jimis2001
- nucomer
- Scandal
- harry akritas
- Thanos_D
- Stroka
- Athens2002
- leo41
- tsiobieman
- Monster Hunter
- Bgpanos
- American Economist
- TonyMontanaEse
- Cortes
- igeorgeoikonomo
- Unseen skygge
- PanosBat
- the purge
- BioChemical
- Meow
- Λαμπρινηη
- Vold
- J.Cameron
- Panagiotis849
- Johnman97
- Memetchi
- Drglitterstar
- kiyoshi
- SlimShady
- MarcoReus
- nicole1982
- Φινεύς
- Βλα
- Αλκης Κ.
- Kostakis45
- giannhs2001
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki

