lowbaper92
Πολύ δραστήριο μέλος


Αρκετά καλό διαγωνισματάκι.
Θέμα 4ο
β)Μήπως έχεις κάνει λάθος στην g(x)??
Όντως..g(x)=f(x)-x
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
lowbaper92
Πολύ δραστήριο μέλος


Παρτε 2 καλες
Θεμα 1ο
g:R->R συνεχης και γν.αυξουσα
3)Θεωρουμε τη συναρτηση :
, δειξτε οτι η
εχει μια τουλαχιστον ριζα στο
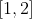
Το |z-3| που εχεις στη συναρτηση ποιο ειναι το μέγιστο ή το ελάχιστο?
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
jimmy007
Εκκολαπτόμενο μέλος


συμφωνω με τα παραπανω.. αλλα βαζε spoiler αλλη φορα
Δεν μου πολυ αρεσε η δικαιολογηση σου στο θεμα 4ο Α - β ερωτημα ..
OK για το spoiler. Τι εννοείς δεν σου αρέσει?? Επειδή είναι πολύ σύντομη??
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
coheNakatos
Δραστήριο μέλος


-----------------------------------------
Όντως..g(x)=f(x)-x
τοτε τριωνυμο με αρνητικη διακρινουσα αν δεν κανω λαθος
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
jimmy007
Εκκολαπτόμενο μέλος


λαθος δεν ειναι απλα ενταξει μπορεις να πεις οτι το 1 ειναι προφανης ριζα και οτι ειναι μοναδικη πιο απλα
-----------------------------------------
τοτε τριωνυμο με αρνητικη διακρινουσα αν δεν κανω λαθος
Ναι. Εγώ πάντως αυτό που σκέφτηκα. εκείνη την στιγμή είπα.
Το ότι διατηρεί σταθερό πρόσημο αποδεικνύεται επειδή είναι συνεχής και διάφορη του μηδενός..
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
lowbaper92
Πολύ δραστήριο μέλος


λαθος δεν ειναι απλα ενταξει μπορεις να πεις οτι το 1 ειναι προφανης ριζα και οτι ειναι μοναδικη πιο απλα
-----------------------------------------
τοτε τριωνυμο με αρνητικη διακρινουσα αν δεν κανω λαθος
εγω πηρα οτι εστω g(x)=0 και κατεληξα σε ατοπο
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
coheNakatos
Δραστήριο μέλος


Το |z-3| που εχεις στη συναρτηση ποιο ειναι το μέγιστο ή το ελάχιστο?
εδω ειναι το ολο θεμα της ασκησης
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
coheNakatos
Δραστήριο μέλος


Ναι. Εγώ πάντως αυτό που σκέφτηκα. εκείνη την στιγμή είπα.
Το ότι διατηρεί σταθερό πρόσημο αποδεικνύεται επειδή είναι συνεχής και διάφορη του μηδενός..
Αν βρεις πρωτα τον τυπο της βγαινει οπως το πα
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
jimmy007
Εκκολαπτόμενο μέλος


Αν βρεις πρωτα τον τυπο της βγαινει οπως το πα
H g στο τετράγωνο σου βγαίνει τριώνυμο με αρνητική διακρίνουσα και όχι η g.
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
coheNakatos
Δραστήριο μέλος


H g στο τετράγωνο σου βγαίνει τριώνυμο με αρνητική διακρίνουσα και όχι η g.
αρα
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Antonis.1821
Νεοφερμένο μέλος


Δεν έχει σημασία. Σημασία έχει να βρεις τη μεγιστη και ελάχιστη τιμή του |z-3|. Μετα θα δεις...Το |z-3| που εχεις στη συναρτηση ποιο ειναι το μέγιστο ή το ελάχιστο?
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
coheNakatos
Δραστήριο μέλος


Δεν έχει σημασία. Σημασία έχει να βρεις τη μεγιστη και ελάχιστη τιμή του |z-3|. Μετα θα δεις...
Ε ενταξει τωρα ειναι ευκολο


Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
jimmy007
Εκκολαπτόμενο μέλος


Δεν έχει σημασία. Σημασία έχει να βρεις τη μεγιστη και ελάχιστη τιμή του |z-3|. Μετα θα δεις...
Πανεύκολο είναι να το βρεις ρε παιδιά. Ας μου πει κάποιος πως βάζεις spoiler για να βοηθήσω...
Και μία άσκηση δικιά μου(εφαρμογή μάλλον):
Αν f παραγωγίσιμη στο R και f'(x) διάφορη του μηδέν για κάθε x Ε R να δείξετε ότι η f είναι γνησίως μονότονη.
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
g!orgos
Εκκολαπτόμενο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
g!orgos
Εκκολαπτόμενο μέλος


(αρκετα εξυπνη , κυριως για το πως θετεις την ασκηση μιλώντας για την μονοτονια :no1

Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
coheNakatos
Δραστήριο μέλος


Nα πω κατι... Πως αποδεικνυεται οτι η f δεν μηδενιζεται πουθενα ώστε να πουμε ότι διατηρει προσημο στο R για να εκμεταλλευτουμε ότι f(0)>0 ? Ή απλα μπορουμε να βρουμε τους 2 δυνατους τυπους της f και να δοκιμασουμε ποιος δινει f(0)>0 ?
συνεχης και διαφορη του μηδενος αρα διατηρει το προσημο της και σε συνδυασμο με το f(0)>0 απορριπτουμε τον εναν τυπο
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
jimmy007
Εκκολαπτόμενο μέλος


αρα(με συνοπτικες διαδικασιες απορριπτεις το μειον)
Aυτό εννοούσα και εγώ...
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
jimmy007
Εκκολαπτόμενο μέλος


Εστω οτι η f δεν ειναι γνησιως μονότονη. Οπότε θα υπάρχουν χ1 , χ2 τετοια ωστε f(x1)=f(x2)=0 Aπο θεωρημα rolle για την f στο [χ1,χ2] προκυπτει ότι υπαρχει ενα τουλαχιστον ξ ε (χ1,χ2) τετοιο ώστε f ' (ξ) = 0 . άτοπο συμφωνα με την εκφωνηση.. Αρα η f τέμνει τον χχ΄σε ένα σημειο οπότε ειναι γνησιως μονοτονη!
(αρκετα εξυπνη , κυριως για το πως θετεις την ασκηση μιλώντας για την μονοτονια :no1
Υπάρχει ένα προβληματάκι. Αν μία συνάρτηση δεν είναι γν. μονότονη αυτό δεν σημαίνει ότι θα έχει αναγκαστικά 2 τουλάχιστον ρίζες...
Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
g!orgos
Εκκολαπτόμενο μέλος



Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
coheNakatos
Δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 16 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 1 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 289 μέλη διάβασαν αυτό το θέμα:
- Maynard
- foxypup
- Pars3c
- mikke
- thepigod762
- 98.8%chimpanzee
- trifasikodiavasma
- ggl
- ioanna2007
- Hased Babis
- Mariosm.
- infection54
- Jesse_
- topg
- eukleidhs1821
- bill09876
- Debugging_Daemon
- mali
- Joji
- Ness
- Helen06
- Scandal
- synthnightingale
- arko
- BillyTheKid
- Magigi
- Paragontas7000
- Unboxholics
- just some guy
- george777
- Wonderkid
- IceCream05
- Abiogenesis
- GeorgePap2003
- katia.m
- giannhs2001
- paul
- Praxis
- Apocalypse
- shezza94
- desp1naa
- rempelos42
- Sherlockina
- oups
- Dimgeb
- spring day
- KingOfPop
- mpapa
- Chrisa
- Physicsstudent
- tsiobieman
- P.Dam.
- persi
- theodoraooo
- PanosBat
- kost28
- mikriarchitectonissa
- BILL KEXA
- Dr. Gl. Luminous
- Eleftheria2
- Lathy
- bruh_234
- Miranda32
- SlimShady
- kallikd
- nucomer
- alpha.kappa
- Eeeee
- J.Cameron
- Marple
- Kitana
- F1L1PAS
- sophiaa
- VFD59
- papa2g
- το κοριτσι του μαη
- srg96
- Hopeful22
- Φινεύς
- Phys39
- Anta2004
- fairyelly
- Pharmacist01
- jYanniss
- Panagiotis849
- Kokro
- augustine
- Nikoletaant
- Mashiro@Iberan
- margik
- Mammy Nun
- Pastramis
- Σωτηρία
- Appolon
- panosveki
- Nickt23
- igeorgeoikonomo
- Steliosgkougkou
- QWERTY23
- Ameliak
- aladdin
- nimbus
- Φωτεινη Τζα.
- marian
- Georgekk
- xrisamikol
- the purge
- Dora140303
- Machris
- s93060
- Nikitas18
- Stif6
- stav.mdp
- damn
- aekaras 21
- Anthropaki
- Angelos12345
- ioannam
- Μάρκος Βασίλης
- skyway
- Nick2325
- Nala
- Manolo165
- Ryuzaki
- T C
- Devilshjoker
- El_
- George9989
- TonyMontanaEse
- globglogabgalab
- constansn
- barkos
- katerinavld
- fenia
- An_uknown_world
- Jimmis18
- maria2001
- KingPoul
- Xara
- thecrazycretan
- abcdefg12345
- Κλημεντίνη
- ale
- panagiotis G
- mechaniceng
- Giii
- calliope
- Tequila
- natalix
- Cortes
- Alexecon1991
- pepsoula
- Mariaathens
- Lia 2006
- 1205
- παιδι για κλαματα
- Alexandros36k
- alexd99
- chembam
- Specon
- Dr House
- panagiotis23
- Johnman97
- rhymeasylum
- Αννα Τσιτα
- KaterinaL
- Libertus
- LeoDel
- iminspain
- den antexw allh apotyxia
- Λαμπρινηη
- Mendel2003
- Ijt
- drosos
- Κορώνα
- JohnGreek
- Αρχηγος_β3
- alexandra_
- ΘανάσοςG4
- Dimitris9
- Birtjan
- george7cr7
- NickT
- Bgpanos
- JKTHEMAN
- nicole1982
- χημεια4λαιφ
- Stroka
- Kostakis45
- charmander
- leo41
- EiriniS20
- Αριάνα123
- MarilynSt
- iManosX13
- Nefh_
- Viedo
- Βλα
- suaimhneas
- george pol
- kristinbacktoschool
- fearless
- Rene2004
- Steffie88
- Slytherin
- jimnikol21
- Unseen skygge
- cel123
- jul25
- Thanos_D
- Ireneeneri
- tasost
- Mukumbura
- xxxtolis
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki



