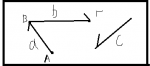
Δινονται τα διανυσματα
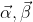
και
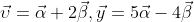
για τα οποια ισχυουν
<90,\vec{\upsilon }\perp \vec{y})
.
Να αποδειξετε οτι
Α.
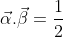
Β.Η γωνια των διανυσματων α και β ειναι 60 μοιρες.
Γ.Τα διανυσματα
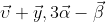
ειναι παραλληλα.
Α. υy=(α+2β)(5α-4β)=α(5α)+α(-4β)+(2β)(5α)+(2β)(-4β)=5(α^2)-4(αβ)+10(αβ)-8(β^2)=5(α^2)-8(β^2)+6(αβ)=5(|α|^2)-8(|β|^2)+6(αβ)
υ κάθετο y => (υ,y)=π/2 => υy=0 => 5(|α|^2)-8(|β|^2)+6(αβ)=0 => αβ=[5(|α|^2)-8(|β|^2)]/6 => αβ=[5*(1^2)-8*(1^2)]/6=3/6=1/2
Άρα αβ=1/2
Β. αβ=|α||β|συν(α,β) => συν(αβ)=αβ/(|α||β|) => συν(α,β)=(1/2)/(1*1)=1/2 => συν(α,β)=συν(π/3)
Άρα (α,β)=2κπ-(π/3) ή (α,β)=2κπ+(π/3) όπου κ ακέραιος. Ξέρουμε ότι 0<(α,β)<π/2
- 0<2κπ-(π/3)<π/2 => π/3<2κπ<5π/6 => 1/6<κ<5/12 => δεν υπάρχει ακέραιος κ στο διάστημα (1/6,5/12)
-0<2κπ+(π/3)<π/2 => -π/2<2κπ<π/6 => -1/4<κ<1/12 => ο μοναδικός ακέραιος στο διάστημα (-1/4,1/12) είναι ο κ=0, οπότε για κ=0 προκύπτει (α,β)=π/3
Άρα (α,β)=π/3 rad =60 μοίρες
Γ.
γ=υ+y => γ=(α+2β)+ (5α-4β) => γ=6α-2β
δ=3α-β
Επομένως γ=6α-2β=2(3α-β)=2δ => γ=2δ => άρα γ//δ και συγκεκριμένα γ ομόρροπο δ
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


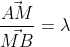 ,
, 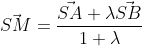
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki