Βοήθεια/Aπορίες στα Μαθηματικά Προσανατολισμού

Guest 856924 · 9 Μαρτίου 2015

θα θελα να μου λυσετε 3 ασκησεις(αναλυτικα)...
ασκηση 1
εστω f παρ/μη στο R και ισχυει για καθε χεR f^3(x)+3f(x)=x^3 + 3x + 3e^x -3
α)να μελετηθει η f ως προς τη μονοτονια και τα ακροτατα
β)να λυθει η εξισωση f(x)=0 και να βρεθει το προσημο της f
γ)αν f γν.αυξουσα στο R να λυθει η ανισωση f(xlnx)>f(-1/2 x^2 +2x -3/2 )

ασκηση 2
α)να μελετηθει ως προς τη μονοτονια οι συναρτησεις
g(x)=e^3x + 2e^x και φ(χ)=x^5+x+3
β)εστω f ορισμενη και συνεχης στο R και ισχυει
e^3f(x) + 2e^f(x)=x^5+x+3 ν.δ.ο f γν.αυξουσα
γ)ν.δ.ο η Cf διερχεται αππο την αρχη των αξονων

ασκηση 3
εστω f παρ/μη στο {-2,2} f(-2)=8 f(2)=-1 και f ' (x)#0 να βρεθει το συνολο τιμων της f

Fedde le Grand · 09-03-15

Έτσι όπως τις βλέπω δε βρίσκω κάτι το ιδιαίτερο. Δε θες να της προσπαθήσεις και να μας ρωτήσεις σε ποιο σημείο κολλάς;

Guest 856924 · 10 Μαρτίου 2015

για να ειμαι ακριβης θα θελα απ την 1 το γ) και απο τη 2 γ)

PiDefiner · 12-03-15

1) Να βρείτε την f(x) αν f''(x)=e^x + 2x, x ανήκει στο R και η Cf τέμνει τον xx' στα σημεία με τετμημένες x0=1 και x1-0.
2) Να βρείτε την f(x) αν f'(x) - 1 = f(x)/x, x>0 και 2f(1)=1
3) Να βρείτε την f στο R με f(x)>0, της οποίας η γραφική παράσταση σε κάθε σημείο της Μ(x,f(x)) έχει εφαπτομένη με συντελεστή διεύθυνσης 4x*sqrt(f(x)) για κάθε x στο R και f(1)=9.

Μπορεί κάποιος να τις λύσει και να μου πει αποτελέσματα για να τα διασταυρώσουμε; Δεν είμαι σίγουρος αν είναι σωστά λυμένες.

Guest 856924 · 12-03-15

Αρχική Δημοσίευση από arnold:
για να ειμαι ακριβης θα θελα απ την 1 το γ) και απο τη 2 γ)

θα θελα λυση σε αυτα γιατι κατι μπερδευω

Fedde le Grand · 12 Μαρτίου 2015

Για το 1γ γνωρίζεις μονοτονία άρα φεύγουν τα f--->μπροστά όλοι οι όροι--->νέα συνάρτηση--->προφανής ρίζα--->Μονοτονία--->ανίσωση και βγαίνει για ποιες τιμές η συνάρτηση σου είναι θετική!

Για το 2ο είναι το εξής. Θες να αποδείξεις ότι f(0)=0. Θέτεις όπου χ=0 και έχεις e^3f(0) + 2ef(0)=3. Θέτεις e^f(x)=y, όλα μπροστά, χορνεράκι και έχεις ότι (y-1)(y^3+y+3)=0. Το τριώνυμο δε μηδενίζεται αφού Δ<0 άρα είναι παντού αρνητικό άρα y=1 και οπότε e^f(0)=1, δηλαδή f(0)=0.

Φίλε PiDefiner τα πρώτα δύο τα έβγαλα: f(x)=e^x + x^2 + c1x + c2 και f(x)=cx - 1

Στo τρίτο δε κατάλαβα τι λες.

Guest 856924 · 13-03-15

Το 1 γ) γραψτο μου μια κανονικα για να δω κατι στο τελος

Fedde le Grand · 13-03-15

Εν τω μεταξύ, είχα κάνει λάθος στη παράγωγο και μου έβγαινε η συνάρτηση γν. αύξουσα παντού αλλά τέσπα. Λοιπόν, η f γνησίως αύξουσα άρα "φεύγουν" τα f, τα πάω μπροστά και έχω g(x)= xlnx + 1/2x^2 -2x + 3/2 με x>0. Είναι g(1)=0. Για χ>0 έχω g'(x)= lnx + x - 1. Παρατηρώ ότι g'(1)=0. Συνεχίζω με 2η παράγωγο και έχω: g''(x)=1/x + 1>0 για κάθε χ ανήκει στο ΠΟ της g. Δηλαδή, η g' είναι γνησίως αύξουσα για χ>0. Οπότε:

χ>1 <=> g'(x)>g'(1) <=> g'(x)>0. (g γν αύξουσα για χ>1)
0<x<1 <=> g'(x)<g'(1) <=> g'(x)<0. (g γν. φθίνουσα για χ>0 και χ<1)

Άρα έτσι προκύπτει και η μονοτονία της g. Αφού έχω βρει προφανή ρίζα για την g, την αξιοποιώ:

x>1 <=> g(x)>g(1) <=> g(x)>0.
0<x<1 <=> g(x)>g(1) <=> g(x)>0.

Οπότε η g είναι θετική για κάθε χ ανήκει στο ΠΟ της g. Αυτό το τελευταίο είναι ουσιαστικά ίδια διαδικασία με τα ακρότατα...

Guest 190013 · 13-03-15

Έχει κανείς αναλυτική απάντηση για την ερώτηση κατανόησης 7 στην σελίδα 295 του σχολικού; Οι επίσημες απαντήσεις την δίνουν σωστή

Λέει:

Αν f, g έχουν στο x0 σημείο καμπής, τότε έχει και η h=f*g Σ - Λ

rebel · 13 Μαρτίου 2015

Νομίζω λάθος. Αντιπαράδειγμα: Οι $f(x)=x^3,\,\,g(x)=-x^3$ παρουσιάζουν σημείο καμπής στο $x_0=0$ αλλά η $h(x)=f(x)g(x)=-x^6$ είναι παντού κοίλη. (Ποιες είναι οι επίσημες απαντήσεις; Γιατί έψαξα στο λυσάρι και δεν έχει)

Guest 190013 · 13-03-15

Μας τις έδωσαν στο σχολείο δεν ξέρω πού τις βρήκαν

eyb0ss · 13-03-15

Αρχική Δημοσίευση από PiDefiner:
1) Να βρείτε την f(x) αν f''(x)=e^x + 2x, x ανήκει στο R και η Cf τέμνει τον xx' στα σημεία με τετμημένες x0=1 και x1-0.
2) Να βρείτε την f(x) αν f'(x) - 1 = f(x)/x, x>0 και 2f(1)=1
3) Να βρείτε την f στο R με f(x)>0, της οποίας η γραφική παράσταση σε κάθε σημείο της Μ(x,f(x)) έχει εφαπτομένη με συντελεστή διεύθυνσης 4x*sqrt(f(x)) για κάθε x στο R και f(1)=9.

Μπορεί κάποιος να τις λύσει και να μου πει αποτελέσματα για να τα διασταυρώσουμε; Δεν είμαι σίγουρος αν είναι σωστά λυμένες.

Επειδή δεν είδα πουθενά λυμένη την 3). Το δεδομένο που δίνει είναι: $f'(x)=4x\sqrt{f(x)}$ . Απλή είναι, αν δεν μπορείς το ξαναβλέπουμε.

PiDefiner · 13-03-15

Αρχική Δημοσίευση από Fedde le Grand:
άρα y=1 και οπότε e^f(0)=1, δηλαδή f(0)=0.

Φίλε PiDefiner τα πρώτα δύο τα έβγαλα: f(x)=e^x + x^2 + c1x + c2 και f(x)=cx - 1

Στo τρίτο δε κατάλαβα τι λες.

Χμ... στο πρώτο μήπως ξέχασες να αντιπαραγώγισεις το x^2 τη δεύτερη φορά; Επίσης αν δεν βαριέσαι, μπορείς να βρεις και τα c;
Όσο για το δεύτερο, δεν ξέρω πως κατέληξες εκεί, έχω τελείως διαφορετικό αποτέλεσμα.

Αρχική Δημοσίευση από mathguy1996:
Επειδή δεν είδα πουθενά λυμένη την 3). Το δεδομένο που δίνει είναι: $f'(x)=4x\sqrt{f(x)}$ . Απλή είναι, αν δεν μπορείς το ξαναβλέπουμε.

Τις έχω λύσεις όλες, όπως είπα, απλά θέλω να σιγουρέψω πως δεν τις έκανα λάθος (π.χ. κάποια αντιπαραγώγιση), γι' αυτό ζήτησα να διασταυρώσω με κάποιον αποτελέσματα. Γράφω τι βρήκα στο καθένα και αν θες να γράψω ολόκληρες τις λύσεις μου, πες μου.

1) f(x) = e^x + (x^3)/3 +x(2/3 - e) -1
2) f(x) = xlnx + x/2
3) f(x) - (x^2 + 2)^2

Fedde le Grand · 13-03-15

Για το πρώτο, σωστά, έκανα λαθάκι. Το σωστό είναι: f(x)=e^x + x^3/3 + c1x + c2.
*Δε βρίσκω τα c1, c2 επειδή δε καταλαβαίνω ακριβώς τι έγραψες στα σημεία τομής με τον x΄x.

Όσο για το δεύτερο, την έκανα με άλλο τρόπο και μου βγαίνει: f(x)= xlnx + c!

eyb0ss · 13-03-15

Αρχική Δημοσίευση από PiDefiner:
Τις έχω λύσεις όλες, όπως είπα, απλά θέλω να σιγουρέψω πως δεν τις έκανα λάθος (π.χ. κάποια αντιπαραγώγιση), γι' αυτό ζήτησα να διασταυρώσω με κάποιον αποτελέσματα. Γράφω τι βρήκα στο καθένα και αν θες να γράψω ολόκληρες τις λύσεις μου, πες μου.

1) f(x) = e^x + (x^3)/3 +x(2/3 - e) -1
2) f(x) = xlnx + x/2
3) f(x) - (x^2 + 2)^2

Αρχική Δημοσίευση από Fedde le Grand:
Για το πρώτο, σωστά, έκανα λαθάκι. Το σωστό είναι: f(x)=e^x + x^3/3 + c1x + c2.
*Δε βρίσκω τα c1, c2 επειδή δε καταλαβαίνω ακριβώς τι έγραψες στα σημεία τομής με τον x΄x.

Όσο για το δεύτερο, την έκανα με άλλο τρόπο και μου βγαίνει: f(x)= xlnx + c!

Πράγματι, με τα δεδομένα που έδωσε η f είναι
$f(x)=e^x+\frac{x^3}{3}-\frac{3e+1}{3}x$ που τέμνει τους άξονες στα σημεία (0,1) και (1,0).
Δεν ξέρω πως βρήκε ο Pi την f έτσι.

Fedde le Grand · 13-03-15

mathguy έχω μια απορία: Στη δεύτερη άσκηση που παραθέτει την κάνω με δύο τρόπους και για κάποιο λόγο βγάζω διαφορετικά αποτελέσματα. Ο πρώτος είναι με παράγωγο πηλίκου και ο δεύτερος είναι πολλαπλασιάζοντας όλους τους όρους με e^-lnx!

Που κάνω την πατάτα;

eyb0ss · 13-03-15

Αρχική Δημοσίευση από Fedde le Grand:
mathguy έχω μια απορία: Στη δεύτερη άσκηση που παραθέτει την κάνω με δύο τρόπους και για κάποιο λόγο βγάζω διαφορετικά αποτελέσματα. Ο πρώτος είναι με παράγωγο πηλίκου και ο δεύτερος είναι πολλαπλασιάζοντας όλους τους όρους με e^-lnx!

Που κάνω την πατάτα;

Σε καμιά πράξη παίζει να κάνεις λάθος. Τέλος πάντων, η δοσμένη είναι ισοδύναμη με την $f'(x)-xf(x)=x$ πολλαπλασιάζουμε με $e^{-lnx}=\frac{1}{e^{lnx}}=\frac{1}{x}$
$\frac{1}{x}f'(x)-\frac{1}{x^2}f(x)=\frac{1}{x} \Leftrightarrow \left(\frac{f(x)}{x}\right)'=(lnx)'$ άρα $\frac{f(x)}{x}=lnx+c \Leftrightarrow f(x)=xlnx+cx$

PiDefiner · 14 Μαρτίου 2015

Αρχική Δημοσίευση από Fedde le Grand:
Για το πρώτο, σωστά, έκανα λαθάκι. Το σωστό είναι: f(x)=e^x + x^3/3 + c1x + c2.
*Δε βρίσκω τα c1, c2 επειδή δε καταλαβαίνω ακριβώς τι έγραψες στα σημεία τομής με τον x΄x.

Όσο για το δεύτερο, την έκανα με άλλο τρόπο και μου βγαίνει: f(x)= xlnx + c!

Λοιπόν, ας τα πάρω με τη σειρά. Καταρχάς για το 1ο, έχεις δίκιο, τώρα είδα πως το έγραψα. Εννοούσα "τέμνει τον xx' στα σημεία με τετμημένες 1 και 0 (x1=1 και x2=0)

Αρχική Δημοσίευση από mathguy1996:
Πράγματι, με τα δεδομένα που έδωσε η f είναι
$f(x)=e^x+\frac{x^3}{3}-\frac{3e+1}{3}x$ που τέμνει τους άξονες στα σημεία (0,1) και (1,0).
Δεν ξέρω πως βρήκε ο Pi την f έτσι.

Αυτό που έγραψα από πάνω (το διορθωμένο), δεν σημαίνει πως f(1)=f(0)=0;

Αρχική Δημοσίευση από Fedde le Grand:
mathguy έχω μια απορία: Στη δεύτερη άσκηση που παραθέτει την κάνω με δύο τρόπους και για κάποιο λόγο βγάζω διαφορετικά αποτελέσματα. Ο πρώτος είναι με παράγωγο πηλίκου και ο δεύτερος είναι πολλαπλασιάζοντας όλους τους όρους με e^-lnx!

Που κάνω την πατάτα;

Εγώ, πάντως, αφού πολλαπλασιάσω με x και καταλήξω στην 1η σχέση του mathguy, διαιρώ με το x^2 (x το δίνει θετικό) και κάνω αντιπαραγώγιση.

Αρχική Δημοσίευση από mathguy1996:
Σε καμιά πράξη παίζει να κάνεις λάθος. Τέλος πάντων, η δοσμένη είναι ισοδύναμη με την $f'(x)-xf(x)=x$ πολλαπλασιάζουμε με $e^{-lnx}=\frac{1}{e^{lnx}}=\frac{1}{x}$
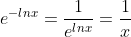
$\frac{1}{x}f'(x)-\frac{1}{x^2}f(x)=\frac{1}{x} \Leftrightarrow \left(\frac{f(x)}{x}\right)'=(lnx)'$ άρα $\frac{f(x)}{x}=lnx+c \Leftrightarrow f(x)=xlnx+cx$

Σε αυτό συμφωνούμε. Αν βάλεις και όπου x το 1 βρίσκεις το c=1/2.

Edit: Βάζω ακόμα μια. Σε αυτή χρειάζομαι, όμως βοήθεια.
Δίνεται η συνάρτηση $\sqrt[3]{x^3-2x^2+x}$ και πρέπει να βρω την μονοτονία της. Όταν την κάνω $(x^3-2x^2+x)^\1/3$ , δεν πρέπει να βάλω και απόλυτο; Και μετά να την κάνω κλαδωτή; Αυτό το έκανα, και βρήκα ότι αλλάζει πρόσημο (και τύπο) στο 0 (αν παραγοντοποιήσουμε το πολυώνυμο), και μετά παραγώγισα (στο μηδέν δεν είναι παραγωγίσιμη). Μπορεί κάποιος να μου πεις πως γίνεται η κλαδωτή και η παράγωγός της, γιατί το έχω μπερδέψει έτσι όπως το έκανα. Αν θέλετε στέλνω φωτογραφία (είναι πολύ μπέρδεμα για να τη γράψω σε latex), αλλά το πιο πιθανό είναι ότι δεν θα καταλάβετε τα γράμματά μου

eyb0ss · 14 Μαρτίου 2015

Αρχική Δημοσίευση από Pidefiner:
Edit: Βάζω ακόμα μια. Σε αυτή χρειάζομαι, όμως βοήθεια.
Δίνεται η συνάρτηση $\sqrt[3]{x^3-2x^2+x}$ και πρέπει να βρω την μονοτονία της. Όταν την κάνω $(x^3-2x^2+x)^\1/3$ , δεν πρέπει να βάλω και απόλυτο; Και μετά να την κάνω κλαδωτή; Αυτό το έκανα, και βρήκα ότι αλλάζει πρόσημο (και τύπο) στο 0 (αν παραγοντοποιήσουμε το πολυώνυμο), και μετά παραγώγισα (στο μηδέν δεν είναι παραγωγίσιμη). Μπορεί κάποιος να μου πεις πως γίνεται η κλαδωτή και η παράγωγός της, γιατί το έχω μπερδέψει έτσι όπως το έκανα. Αν θέλετε στέλνω φωτογραφία (είναι πολύ μπέρδεμα για να τη γράψω σε latex), αλλά το πιο πιθανό είναι ότι δεν θα καταλάβετε τα γράμματά μου

Έστω $h(x)=\sqrt[3]{x}, x\in \mathbb{R}$ και $g(x)=x^3-2x^2+x, x\in \mathbb{R}$ . Προφανώς θα είναι
$f=h\circ g \Rightarrow f(x)=h(g(x))$ .
Η $h$ είναι παντού παραγωγίσιμη με εξαίρεση το 0 οπότε για να δούμε που η $f$ δεν είναι παραγωγίσιμη αρκεί να λύσουμε την εξίσωση $g(x)=0$ .
Έχουμε $g(x)=0 \Leftrightarrow x^3-2x^2+x=0 \Leftrightarrow x(x^2-2x+1)=0 \Leftrightarrow x(x-1)^2=0$ άρα
$x=0\cup x=1$ . Δηλαδή η $f$ είναι παντού παραγωγίσιμη με εξαίρεση τα 0 και 1 (Μέσω ορισμού γνωρίζουμε ότι η $h(g(x))$ είναι παραγωγίσιμη στο $x_0$ όταν η $g$ είναι παραγωγίσιμη στο $x_0$ και $h$ είναι παραγωγίσιμη στο $g(x_0)$ ).
Για $x_1,x_2\in \mathbb{R}$ με $x_1>x_2$ έχουμε $\sqrt[3]{x_1}>\sqrt[3]{x_2} \Leftrightarrow h(x_1)>h(x_2)$ άρα η $h$ είναι γνησίως αύξουσα. Αρκεί να μελετήσουμε την μονοτονία της $g$ για να βρούμε την μονοτονία της $f$ δηλαδή.
Μονοτονία της $g$ :
Η $g$ είναι παραγωγίσιμη στο $\mathbb{R}$ με $g'(x)=3x^2-4x+1$ με ρίζες 1/3 και 1. Άρα
$g$ γνησίως αύξουσα στα διαστήματα $(-\infty,\frac{1}{3}],[1,+\infty)$ και γνησίως φθίνουσα στο $[\frac{1}{3},1]$ (Με μελέτη προσήμου). Δηλαδή
για $x_1,x_2\in (-\infty,\frac{1}{3}]$ με $x_1>x_2$ έχουμε $g(x_1)>g(x_2) \Leftrightarrow h(g(x_1))>h(g(x_2)) \Leftrightarrow f(x_1)>f(x_2)$ άρα $f$ γνησίως αύξουσα στο $(-\infty,\frac{1}{3}].$

για $x_1,x_2\in [\frac{1}{3},1]$ με $x_1>x_2$ έχουμε $g(x_1)<g(x_2) \Leftrightarrow h(g(x_1))<h(g(x_2)) \Leftrightarrow f(x_1)<f(x_2)$ άρα $f$ γνησίως φθίνουσα στο $[\frac{1}{3},1]$

για $x_1,x_2\in [1,+\infty)$ με $x_1>x_2$ έχουμε $g(x_1)>g(x_2) \Leftrightarrow h(g(x_1))>h(g(x_2)) \Leftrightarrow f(x_1)>f(x_2)$ άρα $f$ γνησίως αύξουσα στο $[1,+\infty)$ .
Δεν χρειάστηκε η παράγωγος της $f$
Στην ουσία η $f$ είναι αύξων μονοτονικός μετασχηματισμός της $g$ για αυτό ακολουθεί την ίδια μονοτονία με αυτήν.
Τώρα που το ξαναβλέπω, το κομμάτι όπου μελετάω την παραγωγισιμότητα της $f$ είναι περιττό και δεν χρειάζεται στη λύση.

PiDefiner · 14-03-15

Χμμ, δεν σκέφτηκα ποτέ ότι θα μπορούσα να την λύσω έτσι. Πάντως και εγώ τα ίδια βρήκα, μόνο που στο 1 ο παρανομαστής της παραγώγου μηδενιζόταν και είχα πρόβλημα, αλλά τώρα που το σκέφτομαι μπορούσα να το απλοποιήσω. Τέλος πάντων. Ευχαριστώ πολύ!

Βοήθεια/Aπορίες στα Μαθηματικά Προσανατολισμού

Guest 856924

Επισκέπτης

Πολύ δραστήριο μέλος

Guest 856924

Επισκέπτης

Δραστήριο μέλος

Guest 856924

Επισκέπτης

Πολύ δραστήριο μέλος

Guest 856924

Επισκέπτης

Πολύ δραστήριο μέλος

Guest 190013

Επισκέπτης

Πολύ δραστήριο μέλος

Guest 190013

Επισκέπτης

Δραστήριο μέλος

Δραστήριο μέλος

Πολύ δραστήριο μέλος

Δραστήριο μέλος

Πολύ δραστήριο μέλος

Δραστήριο μέλος

Δραστήριο μέλος

Δραστήριο μέλος

Δραστήριο μέλος