Trolletarian
Πολύ δραστήριο μέλος


Ας θεωρήσουμε την συνάρτηση f(x)=2x+e^(-x) η οποία είναι συνεχής και παραγωγίσιμη στο R και έχει πρώτη παράγωγο f΄(x)=2-e^(-x). Η συνάρτηση f παρουσιάζει ολικό ελάχιστο για x=-ln2 (αφήνεται ως άσκηση) και έχει τιμή f(-ln2)=2(1-ln2).
Άρα f(x)>=f(-ln2) => 2χ+e^(-x)>=2(1-ln2) => x+e^(-x)>=-x+2(1-ln2)
Επειδή lim(x->-άπειρο)[-x+2(1-ln2)]=+άπειρο τότε lim(x->-άπειρο)(x+e^(-x))=+άπειρο



 γαμάτη λύση,δεν το ήξερα αυτό το τέχνασμα.
γαμάτη λύση,δεν το ήξερα αυτό το τέχνασμα.Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Trolletarian
Πολύ δραστήριο μέλος


εσύ που ήξερες ότι βγαίνει άπειρο?Δε μου κάνει για σχολική βασικά. Νομίζω πως ξεφεύγει λίγο από τα σχολικά πλαίσια.
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
koum
Πολύ δραστήριο μέλος


εσύ που ήξερες ότι βγαίνει άπειρο?
Έκανα γραφική παράσταση.
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος


γαμάτη λύση,δεν το ήξερα αυτό το τέχνασμα.
Thanks

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Trolletarian
Πολύ δραστήριο μέλος


Έκανα γραφική παράσταση.
ναι δίκαιο έχεις, και απο εκεί το καταλαβαίνεις ,αλλά εγώ ήθελα απόδειξη.
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
red span
Δραστήριο μέλος


μπορω να το σπασω δηλ φ(χ)=1 και γ(χ)=5 ????

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Gina54
Εκκολαπτόμενο μέλος


Εχει κανεις καμια ιδεα?
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Ricky
Εκκολαπτόμενο μέλος


Aν η συναρτηση f :R -->R ειναι παραγωγισιμη να βρειτε : την f ' (1) οταν f(του x τετραγωνο)= f τετραγωνο του(χ) , χ ανηκει στο R και f(1) διαφορετικο του 1
Εχει κανεις καμια ιδεα?
Δοκίμασε να παραγωγίσεις τη σχέση
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
koum
Πολύ δραστήριο μέλος


Aν η συναρτηση f :R -->R ειναι παραγωγισιμη να βρειτε : την f ' (1) οταν f(του x τετραγωνο)= f τετραγωνο του(χ) , χ ανηκει στο R και f(1) διαφορετικο του 1
Εχει κανεις καμια ιδεα?
Απλά παραγωγίζεις τη δοθείσα σχέση.

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Gina54
Εκκολαπτόμενο μέλος


Ευχαριστώ για τη βοηθεια
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


για βρείτε αυτό το όριο:
ε=e
Και μια λιγότερο κομψή λύση
και απο De L'Hospital
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Μιχάλης9867
Πολύ δραστήριο μέλος


(φ(χ)-1)(γ(χ)-5)=0
μπορω να το σπασω δηλ φ(χ)=1 ή γ(χ)=5 ????
προφανως και δεν αποκλειεται να ειναι και η φ και γ 0 αλλα αρκει το ή
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
emily zola
Νεοφερμένο μέλος


Να δείξετε ότι δεν έχει πραγματικές ρίζες
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Metal-Militiaman
Νεοφερμένο μέλος


(φ(χ)-1)(γ(χ)-5)=0
μπορω να το σπασω δηλ φ(χ)=1 και γ(χ)=5 ????
Προφανώς εννοείς ή και όχι και.
Στα μαθηματικά το "ή" σημαίνει ή το ένα ή το άλλο ή και τα δύο δηλαδή εαν έχεις αβ=0 τότε α=0 ή β=0 ή α=0 και β=0 αλλά
το τελευταίο "ή" παραλείπεται διότι εννοείται οπότε λες α=0 ή β=0 .
Για τις συναρτήσεις όμως υπάρχει περίπτωση να μην ισχύει ο παραπάνω προτασιακός τύπος για κάποια
Σε αφήνω να το βρεις μόνος σου.Τέτοια προβληματάκια είναι καλό να τα παλεύεις όσο μπορείς.
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
emily zola
Νεοφερμένο μέλος


Ευχαριστώ πολύ για την βοήθεια!Η συνάρτησηείναι παραγωγίσιμη στο
με
Άρα η f παρουσιάζει ελάχιστο για
οπότε
και επομένως δεν έχει ρίζα στο
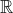

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
red span
Δραστήριο μέλος


Εκανα λαθος εννουσα ''η'' προφανως το καταλαβες το παλεψα αρκετη ωρα διαβασα οτι πρεπει να κανεις επλαηθευση αλλα δεν πολυ καταλαβα δηλαδη το ιδιο ισχυει και για τις λυσεις της δευτεροβαθμιας δηλ Φ²(Χ)+5Φ(Χ)-6=0 ΔΕΝ ΜΠΡΟΩ να πω Φ(χ)=1 η φ(χ)=-6Προφανώς εννοείς ή και όχι και.
Στα μαθηματικά το "ή" σημαίνει ή το ένα ή το άλλο ή και τα δύο δηλαδή εαν έχεις αβ=0 τότε α=0 ή β=0 ή α=0 και β=0 αλλά
το τελευταίο "ή" παραλείπεται διότι εννοείται οπότε λες α=0 ή β=0 .
Για τις συναρτήσεις όμως υπάρχει περίπτωση να μην ισχύει ο παραπάνω προτασιακός τύπος για κάποια.
Σε αφήνω να το βρεις μόνος σου.Τέτοια προβληματάκια είναι καλό να τα παλεύεις όσο μπορείς.
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Metal-Militiaman
Νεοφερμένο μέλος


Εκανα λαθος εννουσα ''η'' προφανως το καταλαβες το παλεψα αρκετη ωρα διαβασα οτι πρεπει να κανεις επλαηθευση αλλα δεν πολυ καταλαβα δηλαδη το ιδιο ισχυει και για τις λυσεις της δευτεροβαθμιας δηλ Φ²(Χ)+5Φ(Χ)-6=0 ΔΕΝ ΜΠΡΟΩ να πω Φ(χ)=1 η φ(χ)=-6
Εάν η f είναι ορισμένη ώστε να ικανοποιηεί την εξίσωση
Θεωρείς λοιπόν ότι η f είναι διπλού τύπου.
Έστω a,b Ε A ώστε f(a)=1 και f(b)=-6 άρα για χ=a και y=b έχουμε
f(a)f(b)+5f(a)-6=0
ή 1*(-6)+5*1-6=0
ή -7=0, άτοπο.
Επομένως f(x)=1 ή f(x)=-6 , xE A .
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
red span
Δραστήριο μέλος


δηλαδη διπλου τυπου να υπαρχουν αλλα α,β που να επαληθευουν την εξισωσηΕάν η f είναι ορισμένη ώστε να ικανοποιηεί την εξίσωσητότε μπορείς να πεις ότι f(χ)=1 ή f(x)=-6(συμπεριλαμβανομένης της περίπτωσης που ίσχυουν και τα δυο προφανώς για διαφορετικά x). Όμως όταν σου δίνεται μία σχέση για την f με x,y για παράδειγμα f(x)f(y)+5f(x)-6=0 και χ,yΕ A=Π.Ο.(f) που για χ=y είναι
τότε πρέπει να απορρίψεις την περίπτωση διπλού τύπου .
Θεωρείς λοιπόν ότι η f είναι διπλού τύπου.
Έστω a,b Ε A ώστε f(a)=1 και f(b)=-6 άρα για χ=a και y=b έχουμε
f(a)f(b)+5f(a)-6=0
ή 1*(-6)+5*1-6=0
ή -7=0, άτοπο.
Επομένως f(x)=1 ή f(x)=-6 , xE A .
Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Θάλεια
Διάσημο μέλος


α)Αν
β)Αν
ι)το γεωμετρικο τοπο των εικονων
ιι)τη μεγιστη τιμη του
εχει κανενας καμια ιδεα;;;

Σημείωση: Το μήνυμα αυτό γράφτηκε 15 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 3 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 232 μέλη διάβασαν αυτό το θέμα:
- Hased Babis
- ChrisG152
- giorgos5002
- Kougami
- giannis06
- Panagiwths12
- mikke
- hristosdab
- trifasikodiavasma
- haji
- thepigod762
- Mariosm.
- soulatso
- oteletampis
- phleidhs
- AggelikiGr
- sir ImPeCaBlE
- veiNqh
- Scandal
- alekos
- Debugging_Daemon
- just some guy
- xristosgkm
- ismember
- Apocalypse
- arrow25
- rempelos42
- ggl
- GStef
- QWERTY23
- xrisamikol
- Σωτηρία
- nikoletaz57
- _Aggelos123
- Mariam38
- SlimShady
- strsismos88
- Georgekk
- Lia 2006
- igeorgeoikonomo
- marian
- tsiobieman
- constansn
- Xristosdimitra
- Panagiotis849
- ρενακι 13
- Memetchi
- eukleidhs1821
- Nikkkpat
- Unboxholics
- korlef
- kwstaseL
- Thanos_D
- the purge
- T C
- Giii
- Papachrist
- liaiscool
- Αννα Τσιτα
- globglogabgalab
- Pharmacist01
- otinanai123
- abcdefg12345
- nicole1982
- thecrazycretan
- Ουριήλ
- kvstas92
- KingOfPop
- maria301
- Poirot
- papa2g
- stefan
- Κλημεντίνη
- TonyMontanaEse
- Lathy
- Alexecon1991
- Μάρκος Βασίλης
- Cortes
- το κοριτσι του μαη
- calliope
- ale
- panagiotis G
- Kleanth
- aggelosst9
- BioChemical
- spring day
- nucomer
- Georgia110
- LeoDel
- pink_panther
- Alexandros973
- marsenis
- den antexw allh apotyxia
- KaterinaL
- kiyoshi
- drosos
- Λαμπρινηη
- Bill22
- Chrysablac.
- giorgosp97
- Βλα
- Monster Hunter
- jul25
- xxxtolis
- Stroka
- nicks1999
- totiloz
- Earendil
- mitsakos
- tasost
- lnesb
- ssalex
- alan09
- Livaja10
- χημεια4λαιφ
- Viedo
- UncleJ
- Kostakis45
- Infrared
- Zgian
- pepatogourounaki
- hirasawayui
- GeoCommand
- Eleni54
- American Economist
- EiriniS20
- ΘανάσοςG4
- stamoul1s
- Αριάνα123
- uni77
- Libertus
- tasoss
- PanosCh002
- Unseen skygge
- Νικόλας Ραπ.
- cel123
- The Limit Does Not Exist
- don_vito
- suaimhneas
- Αλκης Κ.
- alexrami
- Baggelitsa36
- Νομικάριος13
- spinalgr1990
- d_th
- Adolfo valencia
- Πα.Κ
- Vasilis25
- Johnman97
- Steffie88
- rekcoR
- gwgw_5
- fockos
- Mariahj
- roud
- kostas83
- Cpt.Philips
- Makis45
- Χρησλου
- Panos_02
- Vold
- tymvorixos
- GiorgosAsi
- Neos167
- theodoraooo
- George187
- Άρτεμις Α.
- Μαρία2222
- christos87
- Idontknoww
- jimis2001
- Metamorph
- Γατόπαρδος.
- Johnsk
- mitsos14
- johnsiak
- Elel
- Dreamer_SW
- Γιαννης1987Θεσσ
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki



