arko
Εκκολαπτόμενο μέλος
Ο Κωνσταντίνος αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 20 ετών και Φοιτητής του τμήματος Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών ΕΜΠ. Έχει γράψει 177 μηνύματα.

10-04-23

13:04
Ολοκλήρωμα 01 (f(x)-αx)^2
Cade
Πολύ δραστήριο μέλος
Ο Cade αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Απόφοιτος λυκείου. Έχει γράψει 872 μηνύματα.

11-04-23

03:49
τελευταία
Δίνεται συνάρτηση f: [0,1] -> R παραγωγίσιμη, τέτοια, ώστε ∀xε[0,1] να ισχύει :
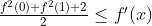 .
.
Να βρεθούν οι τιμές f(0), f(1) και ο τύπος της f
Δίνεται συνάρτηση f: [0,1] -> R παραγωγίσιμη, τέτοια, ώστε ∀xε[0,1] να ισχύει :
Να βρεθούν οι τιμές f(0), f(1) και ο τύπος της f
arko
Εκκολαπτόμενο μέλος
Ο Κωνσταντίνος αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 20 ετών και Φοιτητής του τμήματος Ηλεκτρολόγων Μηχανικών & Μηχανικών Υπολογιστών ΕΜΠ. Έχει γράψει 177 μηνύματα.

11-04-23

15:46
Πολύ πρωτότυπη άσκηση, από πού την πήρες?τελευταία
Δίνεται συνάρτηση f: [0,1] -> R παραγωγίσιμη, τέτοια, ώστε ∀xε[0,1] να ισχύει :
View attachment 114517.
Να βρεθούν οι τιμές f(0), f(1) και ο τύπος της f
ΘΜΤ [0,1]
ΘΜΤ [0,χ], [χ,1]
Guest 749981
Επισκέπτης
αυτή τη στιγμή δεν είναι συνδεδεμέν. Δεν έχει γράψει κανένα μήνυμα.

14-04-23

17:08
Για μια δις παραγωγίσιμη συνάρτηση f: [0,1] -> ℝ ισχύει f(xy) = f(x) + f(y). Νδο η f"(x) = 0 έχει ρίζα στο [0,1].
Για μια συνεχή συνάρτηση f: ℝ -> ℝ ισχύει f(x+y) = f(x) + f(y) αν και μόνο αν f(nx) = nf(x), όπου n∈ℝ* και x∈ℝ. Σωστό ή λάθος;
Για μια συνεχή συνάρτηση f: ℝ -> ℝ ισχύει f(x+y) = f(x) + f(y) αν και μόνο αν f(nx) = nf(x), όπου n∈ℝ* και x∈ℝ. Σωστό ή λάθος;
Panzerkampfwagen
Διάσημο μέλος
Ο Panzerkampfwagen αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Φοιτητής του τμήματος Νομικής ΑΠΘ. Έχει γράψει 3.610 μηνύματα.

14-04-23

21:50
Μαλακία άσκηση για λυκειακά πλαίσια γιατί είναι εκτός τόπου και χρόνου.Για μια δις παραγωγίσιμη συνάρτηση f: [0,1] -> ℝ ισχύει f(xy) = f(x) + f(y). Νδο η f"(x) = 0 έχει ρίζα στο [0,1].
Για μια συνεχή συνάρτηση f: ℝ -> ℝ ισχύει f(x+y) = f(x) + f(y) αν και μόνο αν f(nx) = nf(x), όπου n∈ℝ* και x∈ℝ. Σωστό ή λάθος;
Για ποιόν λόγο να μπλέξεις Συναρτησιακή Εξίσωση Cauchy στο 18χρονο με την απόδειξη ότι είναι Q-γραμμική;
Λύση ενδεικτικά:

και η αντίστροφη
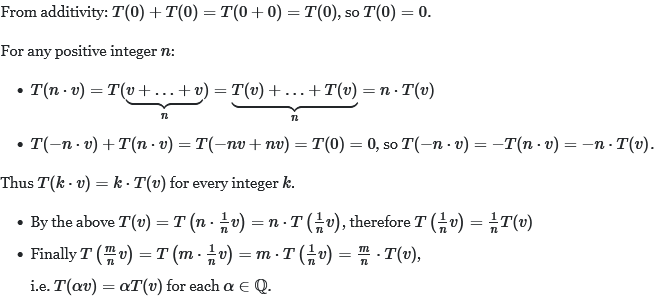
Τώρα για το πρώτο, πάλι από συναρτησιακή ανάλυση θέτεις g(x) = f(e^x) και τότε
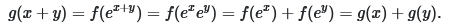
Απλά ειλικρινά για ποιόν λόγο ένας μαθητής γ λυκ να ξέρει τέτοιες πολύ συγκεκριμένες και σύνθετες παπαρολογίες; Σκέψου εγώ έχω κάνει και συναρτησιακή ανάλυση και πάλι έπρεπε να ψάξω να τα βρω.
Guest 749981
Επισκέπτης
αυτή τη στιγμή δεν είναι συνδεδεμέν. Δεν έχει γράψει κανένα μήνυμα.

14-04-23

22:11
Την πρώτη την έβγαλα με γ' λυκείου, για την δεύτερη δεν ξέρωΜαλακία άσκηση για λυκειακά πλαίσια γιατί είναι εκτός τόπου και χρόνου.
Για ποιόν λόγο να μπλέξεις Συναρτησιακή Εξίσωση Cauchy στο 18χρονο με την απόδειξη ότι είναι Q-γραμμική;
Λύση ενδεικτικά:

και η αντίστροφη
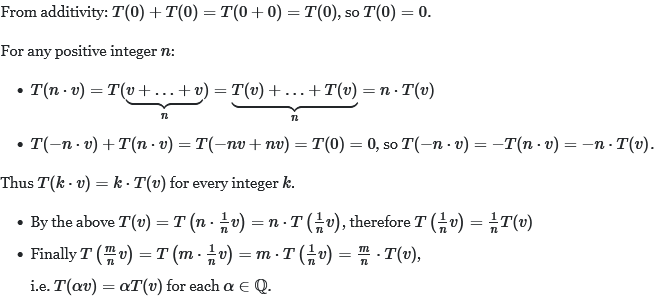
Τώρα για το πρώτο, πάλι από συναρτησιακή ανάλυση θέτεις g(x) = f(e^x) και τότε
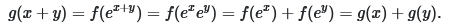
Απλά ειλικρινά για ποιόν λόγο ένας μαθητής γ λυκ να ξέρει τέτοιες πολύ συγκεκριμένες και σύνθετες παπαρολογίες; Σκέψου εγώ έχω κάνει και συναρτησιακή ανάλυση και πάλι έπρεπε να ψάξω να τα βρω.
IceCream05
Νεοφερμένο μέλος
Η IceCream05 αυτή τη στιγμή δεν είναι συνδεδεμένη. Είναι 20 ετών και Μαθήτρια Γ' λυκείου. Έχει γράψει 37 μηνύματα.
Cade
Πολύ δραστήριο μέλος
Ο Cade αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Απόφοιτος λυκείου. Έχει γράψει 872 μηνύματα.

15-04-23

02:51
Α. Προκύπτει άμεσα από θ.Fermat.
Β. ΘΜΤ.
Γ. Θέτουμε x = f(u) στο πρώτο μέλος της ισότητας κ με πράξεις καταλήγουμε στην αρχική ανισότητα του ξ
Δ. Ολοκληρώνοντας κατά παραγοντες παίρνουμε ότι f'(1)=f(1)-f(0) οπότε με διαδοχική εφαρμογη του ΘΜΤ υπάρχει ξε(0,1) : f'(ξ) = f(1)-f(0) και
ρε(ξ,1) : f"(ρ) = f'(1)-f'(ξ)/(1-ξ) απ' όπου λαμβάνουμε
f"(ρ)=0
Β. ΘΜΤ.
Γ. Θέτουμε x = f(u) στο πρώτο μέλος της ισότητας κ με πράξεις καταλήγουμε στην αρχική ανισότητα του ξ
Δ. Ολοκληρώνοντας κατά παραγοντες παίρνουμε ότι f'(1)=f(1)-f(0) οπότε με διαδοχική εφαρμογη του ΘΜΤ υπάρχει ξε(0,1) : f'(ξ) = f(1)-f(0) και
ρε(ξ,1) : f"(ρ) = f'(1)-f'(ξ)/(1-ξ) απ' όπου λαμβάνουμε
f"(ρ)=0
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.965 μηνύματα.

15-04-23

15:16
ωραιο ερωτηματακι για το πρωτο για δ1.δεν εχουν βαλει ποτε να υπολογισεις ορισμενο ολοκληρωμα μεσω fermat και ειναι ενδιαφερον οτι το lnx το βγαζεις εξω ως σταθερα.
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.965 μηνύματα.

15-04-23

16:32
οτι να ναι γενικως!Βαριεμαι και να κατσω να ασχοληθω να λυσω τετοιες ασκησεις.Μαλακία άσκηση για λυκειακά πλαίσια γιατί είναι εκτός τόπου και χρόνου.
Για ποιόν λόγο να μπλέξεις Συναρτησιακή Εξίσωση Cauchy στο 18χρονο με την απόδειξη ότι είναι Q-γραμμική;
Λύση ενδεικτικά:

και η αντίστροφη
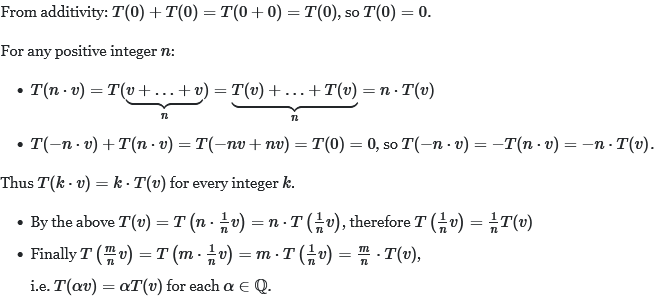
Τώρα για το πρώτο, πάλι από συναρτησιακή ανάλυση θέτεις g(x) = f(e^x) και τότε
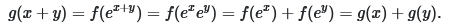
Απλά ειλικρινά για ποιόν λόγο ένας μαθητής γ λυκ να ξέρει τέτοιες πολύ συγκεκριμένες και σύνθετες παπαρολογίες; Σκέψου εγώ έχω κάνει και συναρτησιακή ανάλυση και πάλι έπρεπε να ψάξω να τα βρω.
Panzerkampfwagen
Διάσημο μέλος
Ο Panzerkampfwagen αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Φοιτητής του τμήματος Νομικής ΑΠΘ. Έχει γράψει 3.610 μηνύματα.

15-04-23

16:33
Τα μαθηματικά λυκείου είναι μακραν το πιο τοξικό μάθημα γιατί οποιοσδήποτε παίρνει ασκήσεις πανεπιστημιακού επιπέδου, τις γαμάει τη μάνα για να τις βγάλει με εργαλεία Γ' Λυκείου και τις λέει "Επαναληπτικές".οτι να ναι γενικως!Βαριεμαι και να κατσω να ασχοληθω να λυσω τετοιες ασκησεις.
Τέτοιες έβρισκα και εγώ και έκλαιγα όταν έδινα γιατί αντικειμενικά δεν λύνονται.
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.965 μηνύματα.

15-04-23

16:34
μα δεν υπαρχει περιπτωση να βαλουν ποτε τετοια ερωτηματα.το θεμα ειναι λυνουν υποψηφιοι θεματα οπως αυτο με το fermat κτλπ.αυτα ειναι επικινδυνα για εξετασειςΤα μαθηματικά λυκείου είναι μακραν το πιο τοξικό μάθημα γιατί οποιοσδήποτε παίρνει ασκήσεις πανεπιστημιακού επιπέδου, τις γαμάει τη μάνα για να τις βγάλει με εργαλεία Γ' Λυκείου και τις λέει "Επαναληπτικές".
Τέτοιες έβρισκα και εγώ και έκλαιγα όταν έδινα γιατί αντικειμενικά δεν λύνονται.
Panzerkampfwagen
Διάσημο μέλος
Ο Panzerkampfwagen αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Φοιτητής του τμήματος Νομικής ΑΠΘ. Έχει γράψει 3.610 μηνύματα.

15-04-23

16:35
Συμφωνώ απόλυτα.μα δεν υπαρχει περιπτωση να βαλουν ποτε τετοια ερωτηματα.το θεμα ειναι λυνουν υποψηφιοι θεματα οπως αυτο με το fermat κτλπ.αυτα ειναι επικινδυνα για εξετασεις
Cade
Πολύ δραστήριο μέλος
Ο Cade αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Απόφοιτος λυκείου. Έχει γράψει 872 μηνύματα.

16-04-23

21:27
Έστω η παραγωγίσιμη συνάρτηση
f: [0,1] -> R με f(0)=0.
Αν η f είναι κυρτή, να αποδείξετε ότι :
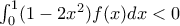
f: [0,1] -> R με f(0)=0.
Αν η f είναι κυρτή, να αποδείξετε ότι :
Cade
Πολύ δραστήριο μέλος
Ο Cade αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Απόφοιτος λυκείου. Έχει γράψει 872 μηνύματα.

18-04-23

23:28
Λύση :
επειδή η f είναι κυρτή, από ΘΜΤ στα διαστήματα

θα υπάρχουν m, n τέτοια ώστε :
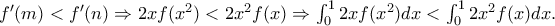
(ισότητα μόνο για x=0 και x=1)
Οπότε αν θέσουμε προκύπτει το ζητούμενο
επειδή η f είναι κυρτή, από ΘΜΤ στα διαστήματα
θα υπάρχουν m, n τέτοια ώστε :
(ισότητα μόνο για x=0 και x=1)
Οπότε αν θέσουμε προκύπτει το ζητούμενο
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.965 μηνύματα.

19-04-23

12:34
παρα πολυ εξυπνη ασκηση.συγχαρητηρια.βεβαια θεωρω οτι χ^2<χ στο (0,1) θελει μια γρηγορη αποδειξηΛύση :
επειδή η f είναι κυρτή, από ΘΜΤ στα διαστήματα
View attachment 114708
θα υπάρχουν m, n τέτοια ώστε :
View attachment 114710
(ισότητα μόνο για x=0 και x=1)
Οπότε αν θέσουμε προκύπτει το ζητούμενο
hl_amhxanos
Πολύ δραστήριο μέλος
Ο Νίκος Κούκος αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 26 ετών, Φοιτητής του τμήματος Λογιστικής & Χρηματοοικονομικής ΟΠΑ και μας γράφει από Αγία Παρασκευή (Αττική). Έχει γράψει 824 μηνύματα.

02-05-23

17:28

Διαγώνισμα Μαθηματικών προσανατολισμού Γ’ Λυκείου!
Ένα ακόμη διαγώνισμα στα Μαθηματικά προσανατολισμού της Γ’ Λυκείου εφ’όλης της ύλης από τον εξαίρετο συνάδελφο Θοδωρή Παγώνη: Διαγώνισμα-Γ-Λυκ-Κατ-28-04-2023Download Καλό Μήνα σε όλους!…
 liveyourmaths.com
liveyourmaths.com
Καλή διασκέδαση
Cade
Πολύ δραστήριο μέλος
Ο Cade αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Απόφοιτος λυκείου. Έχει γράψει 872 μηνύματα.

03-05-23

11:08
Δ2. Η g είναι συνεχής στο R ως πηλίκο συνεχών συναρτήσεων οπότε αρκεί νδο
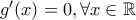
Είναι
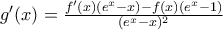
οπότε αν θεωρήσουμε συνάρτηση
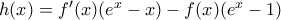
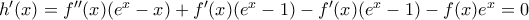
από τη σχέση που δίνεται, άρα h(x) = c1, ∀xεR.
Για x=0 : c1=0 => h(x) = 0 άρα g(x) = c2 => c2 = 1 απ' όπου έπεται ο τύπος της f
Είναι
οπότε αν θεωρήσουμε συνάρτηση
από τη σχέση που δίνεται, άρα h(x) = c1, ∀xεR.
Για x=0 : c1=0 => h(x) = 0 άρα g(x) = c2 => c2 = 1 απ' όπου έπεται ο τύπος της f
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.965 μηνύματα.

03-05-23

15:09
το τεταρτο θεμα θα το περιμενα πολυ πιο δυσκολο.οκ το πρωτο ερωτημα πρεπει να ξερεις την ανισοτητα με το απολυτο ημιτονο χ αλλα οι καλοι μαθητες το γνωριζουν.το δευτερο ερωτημα ειναι ολο πραξεις.το δ3 με το μεγιστο α πολυ πολυ προφανες ενω το τελευταιο ερωτημα παλι προφανες αν εκμεταλλευτεις το ελαχιστο ενω και την κυρτοτητα που σου χει βαλει να τη βρεις επρεπε να υπαρχει καποιο ερωτημα να την αξιοποιησεις.ψιλοπροχειρο θεμα
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 3 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 289 μέλη διάβασαν αυτό το θέμα:
- Maynard
- foxypup
- Pars3c
- mikke
- thepigod762
- 98.8%chimpanzee
- trifasikodiavasma
- ggl
- ioanna2007
- Hased Babis
- Mariosm.
- infection54
- Jesse_
- topg
- eukleidhs1821
- bill09876
- Debugging_Demon
- mali
- Joji
- Ness
- Helen06
- Scandal
- synthnightingale
- arko
- BillyTheKid
- Magigi
- Paragontas7000
- Unboxholics
- just some guy
- george777
- Wonderkid
- Micro
- IceCream05
- Abiogenesis
- GeorgePap2003
- katia.m
- giannhs2001
- paul
- Praxis
- Apocalypse
- shezza94
- desp1naa
- rempelos42
- Sherlockina
- oups
- Dimgeb
- spring day
- KingOfPop
- mpapa
- Chrisa
- Physicsstudent
- tsiobieman
- P.Dam.
- persi
- theodoraooo
- PanosBat
- kost28
- mikriarchitectonissa
- BILL KEXA
- Dr. Gl. Luminous
- Eleftheria2
- Lathy
- bruh_234
- Miranda32
- SlimShady
- kallikd
- nucomer
- alpha.kappa
- Eeeee
- J.Cameron
- Marple
- Kitana
- F1L1PAS
- sophiaa
- VFD59
- papa2g
- το κοριτσι του μαη
- srg96
- Hopeful22
- Φινεύς
- Phys39
- Anta2004
- fairyelly
- Pharmacist01
- jYanniss
- Panagiotis849
- Kokro
- augustine
- Nikoletaant
- Mashiro@Iberan
- margik
- Mammy Nun
- Pastramis
- Σωτηρία
- Appolon
- panosveki
- Nickt23
- igeorgeoikonomo
- Steliosgkougkou
- QWERTY23
- Ameliak
- aladdin
- nimbus
- Φωτεινη Τζα.
- marian
- Georgekk
- xrisamikol
- Poirot
- the purge
- Dora140303
- Machris
- s93060
- Nikitas18
- Stif6
- stav.mdp
- damn
- aekaras 21
- Anthropaki
- Angelos12345
- ioannam
- Μάρκος Βασίλης
- skyway
- Nick2325
- Nala
- Manolo165
- Ryuzaki
- T C
- Devilshjoker
- El_
- George9989
- TonyMontanaEse
- globglogabgalab
- constansn
- barkos
- katerinavld
- fenia
- An_uknown_world
- Jimmis18
- maria2001
- KingPoul
- Xara
- thecrazycretan
- abcdefg12345
- Κλημεντίνη
- ale
- panagiotis G
- mechaniceng
- Giii
- calliope
- Tequila
- natalix
- Ουριήλ
- Cortes
- Alexecon1991
- pepsoula
- Mariaathens
- Lia 2006
- 1205
- παιδι για κλαματα
- Alexandros36k
- alexd99
- chembam
- Specon
- Dr House
- panagiotis23
- Johnman97
- rhymeasylum
- Αννα Τσιτα
- KaterinaL
- Libertus
- LeoDel
- iminspain
- den antexw allh apotyxia
- Λαμπρινηη
- Mendel2003
- Ijt
- drosos
- Κορώνα
- JohnGreek
- Αρχηγος_β3
- alexandra_
- ΘανάσοςG4
- Dimitris9
- Birtjan
- george7cr7
- NickT
- Bgpanos
- JKTHEMAN
- nicole1982
- χημεια4λαιφ
- Stroka
- Kostakis45
- charmander
- leo41
- EiriniS20
- Αριάνα123
- MarilynSt
- iManosX13
- Nefh_
- Viedo
- Βλα
- suaimhneas
- george pol
- kristinbacktoschool
- fearless
- Rene2004
- Steffie88
- Slytherin
- jimnikol21
- Unseen skygge
- cel123
- jul25
- Thanos_D
- Ireneeneri
- tasost
- Mukumbura
- xxxtolis
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki



