Guest 749981
Επισκέπτης
αυτή τη στιγμή δεν είναι συνδεδεμέν. Δεν έχει γράψει κανένα μήνυμα.

03-09-22

17:46
Για το Δ2 επίσης: Έστω Α(χ) = (χf(x) - 1)/(x(x-1)). Για να έχει λύση η Α(χ) = 0 θα πρέπει να υπάρχει χ με f(x) = 1/x, απορρίπτεται λόγω υπόθεσης. Άρα η Α (συνεχής λόγω συνέχειας της f) διατηρεί σταθερό πρόσημο. Από f(2) = ln2, Α(χ) > 0. Άρα f'(x) = -A(x).
Η Δ4 με έκαψε με τις πράξεις.
asdfqwerty
Πολύ δραστήριο μέλος
Ο asdfqwerty αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Φοιτητής του τμήματος Πληροφορικής & Τηλεπικοινωνιών ΕΚΠΑ. Έχει γράψει 1.347 μηνύματα.
Guest 586541
Επισκέπτης
αυτή τη στιγμή δεν είναι συνδεδεμέν. Δεν έχει γράψει κανένα μήνυμα.

13-09-22

03:18
Αρκετα ευκολα θεματα..
Έλυσα το Δ και συμφωνώ, είναι ευκολότερα από τα καλοκαιρινά. Πιο φροντιστηριακά. Το Δ3 φερειπείν, είναι κλασσική άσκηση που διδάσκεται στη συνέχεια.
Το Δ4, αν και με τρικ που συναντάται, ήθελε λίγη παρατηρητικότητα για να βγει. Από εκεί και πέρα τετριμμένο... Κατά τη γνώμη μου στο ίδιο επίπεδο με αυτό των καλοκαιριών ή και πιο εύκολο...
Δ1,Δ2 αστεία, μόνο προσοχή σε πράξεις απαιτεί το Δ2, ενώ στο Δ1 δίνει στο πιάτο το αποτέλεσμα.
Δεν παρατηρώ κάτι ασυνήθιστο σε Α,Β,Γ...
Μάλλον θορυβήθηκαν από τις κενές θέσεις λόγω ΕΒΕ και αποφάσισαν να μαλακώσουν...δεν μας έχουν συνηθίσει σε τόσο βατά στις επαναληπτικές (με εξαίρεση στη κορωνοδιετία, για προφανείς λόγους)...
Cade
Πολύ δραστήριο μέλος
Ο Cade αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Απόφοιτος λυκείου. Έχει γράψει 856 μηνύματα.

13-09-22

06:21
Δεν καταλαβαίνω γιατί έβαλαν τόσο εύκολα Δ3, Δ4, θα μπορούσαν και καλύτερα. Δ3 βγάζει μάτι ότι πρόκειται για θετ από το άθροισμα των συντελεστών που βρίσκεται στον παρανομαστή και Δ4 από το αποτέλεσμα, οπότε πηγαίνοντας ανάποδα βρίσκεις εύκολα την σχέση που πρέπει να ολοκληρώσεις. Γενικά δε βρίσκω κάποια ιδιαίτερη δυσκολία στο διαγώνισμα, ένας σωστά διαβασμένος μαθητής με λίγη προσοχή έγραφε 19-20 για πλάκα.Έλυσα το Δ και συμφωνώ, είναι ευκολότερα από τα καλοκαιρινά. Πιο φροντιστηριακά. Το Δ3 φερειπείν, είναι κλασσική άσκηση που διδάσκεται στη συνέχεια.
Το Δ4, αν και με τρικ που συναντάται, ήθελε λίγη παρατηρητικότητα για να βγει. Από εκεί και πέρα τετριμμένο... Κατά τη γνώμη μου στο ίδιο επίπεδο με αυτό των καλοκαιριών ή και πιο εύκολο...
Δ1,Δ2 αστεία, μόνο προσοχή σε πράξεις απαιτεί το Δ2, ενώ στο Δ1 δίνει στο πιάτο το αποτέλεσμα.
Δεν παρατηρώ κάτι ασυνήθιστο σε Α,Β,Γ...
Μάλλον θορυβήθηκαν από τις κενές θέσεις λόγω ΕΒΕ και αποφάσισαν να μαλακώσουν...δεν μας έχουν συνηθίσει σε τόσο βατά στις επαναληπτικές (με εξαίρεση στη κορωνοδιετία, για προφανείς λόγους)...
Guest 586541
Επισκέπτης
αυτή τη στιγμή δεν είναι συνδεδεμέν. Δεν έχει γράψει κανένα μήνυμα.

13-09-22

10:32
Η μόνη (πολύ) μικρή δυσκολία ήταν στο να θυμηθείς την παράγωγο όταν δεις από τι πρέπει να είναι μεγαλύτερο το ολοκλήρωμα που δίνει και να μην μπερδευτείς στην απόδειξη χρησιμοποιώντας τον πρώτο κλάδο... ήθελε λίγη παρατηρητικότητα και συγκέντρωση, από εκεί και πέρα είναι γνωστό και χιλιοειδωμένο το θέμα...αρκετά εύκολα θέματα γενικά...Δεν καταλαβαίνω γιατί έβαλαν τόσο εύκολα Δ3, Δ4, θα μπορούσαν και καλύτερα. Δ3 βγάζει μάτι ότι πρόκειται για θετ από το άθροισμα των συντελεστών που βρίσκεται στον παρανομαστή και Δ4 από το αποτέλεσμα, οπότε πηγαίνοντας ανάποδα βρίσκεις εύκολα την σχέση που πρέπει να ολοκληρώσεις. Γενικά δε βρίσκω κάποια ιδιαίτερη δυσκολία στο διαγώνισμα, ένας σωστά διαβασμένος μαθητής με λίγη προσοχή έγραφε 19-20 για πλάκα.
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.928 μηνύματα.

13-09-22

19:09
ελα ρε γραφανε πανελληνιες επαναληπτικες το σαββατο? πολυ ωραια θεματα απο οτι βλεπω και πρωτοτυπα που αν πεφτανε σε κανονικες θα σκουζανε 300 χρονια.το β4 αρκετα εξυπνο ερωτημα για να τονιστει η διαφορα οτι αν λεμε ισες συναρτησεις πρεπει να εξετασουμε και το πεδιο ορισμου!!στο γ θεμα γνωστες ιδεες ολα απλα στο τελευταιο πρεπει καποιος να ναι πονηρεμενος να αξιοποιησει την εφαπτομενη.στο δ θεμα τολμησαν και βαλανε την χ^χ!!!αρκετα πονηρο θεμα! το δ1 πρεπει να σαι πολυ προσεκτικος και να σου ερθει αμεσως να το κανεις e^xlnx αλλιως χαιρετας γρηγορα!το δ2 παμπονηρο καθως βαλανε στο ακρο να μηδενιζει η παραγωγος οποτε καποιος πρεπει να ναι γνωστης της θεωριας για να το απορριψει.στο δ3 βαλανε αυτο που δεν εχουνε τολμησει να βαλουνε σε κανονικες θεωρημα μεγιστης και ελαχιστης τιμης οπου πας σε 2 περιπτωσεις με θεωρημα ενδιαμεσων τιμων και το να παρει την ακραια τιμη.ειναι ενα κλασσικο ερωτημα βεβαια που το δουλευουνε απο αρχαιοτατων χρονων τα φροντιστηρια αλλα δεν εχει πεσει ποτε σε πανελλαδικες!και εδω αν δεν το εχεις δουλεψει χαιρετας.το δ4 πρεπει αμεσα να σου κοψει οτι πρεπει να αποδειξεις οτι xf(x)>f'(x) αρκει να πονηρευτεις το δευτερο μελος.δεν ξερω με την κουραση ολου του διαγωνισματος αν καποιος θα το σκεφτει γρηγορα αυτο!
δεν καταλαβαινω γτ τετοια απαξιωση στα θεματα.δηλαδη τι θεματα θελετε?
Αυτόματη ένωση συνεχόμενων μηνυμάτων:
διαφωνω οτι ηταν γελοια θεματα οπως λετε!αν πεφτανε σε κανονικες θα κλαιγανε αρκετοι!το δ3 ναι ειναι δουλεμενο θεμα και το θυμαμαι απλα για καποιον περιεργο λογο σε αυτη τη μορφη δεν το εχουν βαλει ποτε.βαζω στοιχημα οτι αρκετοι θα κολωνανε.επισης,το δ4 ειναι αρκετα πονηρο ερωτημα αν δεν σου ερθει αμεσως.θελει να βλεπεις.επισης,η χ^χ δεν ειναι η πιο γελοια συναρτηση.εχει καποιες παγιδες πχ να απορριψεις το ακρο στο κρισιμο σημειο.ακομα και στο β το β4 δεν ειναι και το πιο συνηθες ερωτημα σε πανελλαδικες που διακρινει μια γνωση.στο γ θεμα το γ4 και αυτο ειναι ωραιο ερωτημα που δεν ειναι αστειο αν δεν εισαι αριστος.Η μόνη (πολύ) μικρή δυσκολία ήταν στο να θυμηθείς την παράγωγο όταν δεις από τι πρέπει να είναι μεγαλύτερο το ολοκλήρωμα που δίνει και να μην μπερδευτείς στην απόδειξη χρησιμοποιώντας τον πρώτο κλάδο... ήθελε λίγη παρατηρητικότητα και συγκέντρωση, από εκεί και πέρα είναι γνωστό και χιλιοειδωμένο το θέμα...αρκετά εύκολα θέματα γενικά...
δεν καταλαβαινω γτ τετοια απαξιωση στα θεματα.δηλαδη τι θεματα θελετε?
Guest 586541
Επισκέπτης
αυτή τη στιγμή δεν είναι συνδεδεμέν. Δεν έχει γράψει κανένα μήνυμα.

13-09-22

19:17
ελα ρε γραφανε πανελληνιες επαναληπτικες το σαββατο? πολυ ωραια θεματα απο οτι βλεπω και πρωτοτυπα που αν πεφτανε σε κανονικες θα σκουζανε 300 χρονια.το β4 αρκετα εξυπνο ερωτημα για να τονιστει η διαφορα οτι αν λεμε ισες συναρτησεις πρεπει να εξετασουμε και το πεδιο ορισμου!!στο γ θεμα γνωστες ιδεες ολα απλα στο τελευταιο πρεπει καποιος να ναι πονηρεμενος να αξιοποιησει την εφαπτομενη.στο δ θεμα τολμησαν και βαλανε την χ^χ!!!αρκετα πονηρο θεμα! το δ1 πρεπει να σαι πολυ προσεκτικος και να σου ερθει αμεσως να το κανεις e^xlnx αλλιως χαιρετας γρηγορα!το δ2 παμπονηρο καθως βαλανε στο ακρο να μηδενιζει η παραγωγος οποτε καποιος πρεπει να ναι γνωστης της θεωριας για να το απορριψει.στο δ3 βαλανε αυτο που δεν εχουνε τολμησει να βαλουνε σε κανονικες θεωρημα μεγιστης και ελαχιστης τιμης οπου πας σε 2 περιπτωσεις με θεωρημα ενδιαμεσων τιμων και το να παρει την ακραια τιμη.ειναι ενα κλασσικο ερωτημα βεβαια που το δουλευουνε απο αρχαιοτατων χρονων τα φροντιστηρια αλλα δεν εχει πεσει ποτε σε πανελλαδικες!και εδω αν δεν το εχεις δουλεψει χαιρετας.το δ4 πρεπει αμεσα να σου κοψει οτι πρεπει να αποδειξεις οτι xf(x)>f'(x) αρκει να πονηρευτεις το δευτερο μελος.δεν ξερω με την κουραση ολου του διαγωνισματος αν καποιος θα το σκεφτει γρηγορα αυτο!
Ε όχι και θα σκούζανε 300 χρόνια...η x^x είναι πολύ γνωστή συνάρτηση και ο οποιοσδήποτε πηγαίνει για 15+ γνωρίζει πώς να τη χειριστεί...ήταν αρκετά ευκολότερα από τα καλοκαιρινά...και βατά σε κάθε περίπτωση...
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.928 μηνύματα.

13-09-22

19:18
διαφωνω καθετως και οριζοντιως.θεμα σαν το δ4 δεν υπηρχε το καλοκαιρι.πολυ πιο δυσκολα θεματα συνολικα.Ε όχι και θα σκούζανε 300 χρόνια...η x^x είναι πολύ γνωστή συνάρτηση και ο οποιοσδήποτε πηγαίνει για 15+ γνωρίζει πώς να τη χειριστεί...ήταν αρκετά ευκολότερα από τα καλοκαιρινά...και βατά εν γένει...
Guest 586541
Επισκέπτης
αυτή τη στιγμή δεν είναι συνδεδεμέν. Δεν έχει γράψει κανένα μήνυμα.

13-09-22

19:21
διαφωνω οτι ηταν γελοια θεματα οπως λετε!αν πεφτανε σε κανονικες θα κλαιγανε αρκετοι!το δ3 ναι ειναι δουλεμενο θεμα και το θυμαμαι απλα για καποιον περιεργο λογο σε αυτη τη μορφη δεν το εχουν βαλει ποτε.βαζω στοιχημα οτι αρκετοι θα κολωνανε.επισης,το δ4 ειναι αρκετα πονηρο ερωτημα αν δεν σου ερθει αμεσως.θελει να βλεπεις.επισης,η χ^χ δεν ειναι η πιο γελοια συναρτηση.εχει καποιες παγιδες πχ να απορριψεις το ακρο στο κρισιμο σημειο.ακομα και στο β το β4 δεν ειναι και το πιο συνηθες ερωτημα σε πανελλαδικες που διακρινει μια γνωση.στο γ θεμα το γ4 και αυτο ειναι ωραιο ερωτημα που δεν ειναι αστειο αν δεν εισαι αριστος.
δεν καταλαβαινω γτ τετοια απαξιωση στα θεματα.δηλαδη τι θεματα θελετε?
Δεν έπεσε κάποιο πρωτότυπο ερώτημα, όπως το φετινό Δ3, το Δ4 του 2019, το Δ3 του 2018, το Δ5 του 2017, κλπ...αναφέρομαι στις κανονικές, ενώ και στις επαναληπτικές έθεταν τέτοιου είδους ερωτήματα...
Cade
Πολύ δραστήριο μέλος
Ο Cade αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Απόφοιτος λυκείου. Έχει γράψει 856 μηνύματα.

13-09-22

19:28
υπερβολές. Ποια γνώση ακριβώς, το οτι ίσες συναρτήσεις λέγονται αυτές που έχουν ίδιο (τύπο) και πεδίο ορισμού; σιγά το πράγμα. Επίσης θεωρώ δεδομένο ότι ένας μαθητής της γ γνωρίζει ποια σημεία λέγονται κρίσιμα.ελα ρε γραφανε πανελληνιες επαναληπτικες το σαββατο? πολυ ωραια θεματα απο οτι βλεπω και πρωτοτυπα που αν πεφτανε σε κανονικες θα σκουζανε 300 χρονια.το β4 αρκετα εξυπνο ερωτημα για να τονιστει η διαφορα οτι αν λεμε ισες συναρτησεις πρεπει να εξετασουμε και το πεδιο ορισμου!!στο γ θεμα γνωστες ιδεες ολα απλα στο τελευταιο πρεπει καποιος να ναι πονηρεμενος να αξιοποιησει την εφαπτομενη.στο δ θεμα τολμησαν και βαλανε την χ^χ!!!αρκετα πονηρο θεμα! το δ1 πρεπει να σαι πολυ προσεκτικος και να σου ερθει αμεσως να το κανεις e^xlnx αλλιως χαιρετας γρηγορα!το δ2 παμπονηρο καθως βαλανε στο ακρο να μηδενιζει η παραγωγος οποτε καποιος πρεπει να ναι γνωστης της θεωριας για να το απορριψει.στο δ3 βαλανε αυτο που δεν εχουνε τολμησει να βαλουνε σε κανονικες θεωρημα μεγιστης και ελαχιστης τιμης οπου πας σε 2 περιπτωσεις με θεωρημα ενδιαμεσων τιμων και το να παρει την ακραια τιμη.ειναι ενα κλασσικο ερωτημα βεβαια που το δουλευουνε απο αρχαιοτατων χρονων τα φροντιστηρια αλλα δεν εχει πεσει ποτε σε πανελλαδικες!και εδω αν δεν το εχεις δουλεψει χαιρετας.το δ4 πρεπει αμεσα να σου κοψει οτι πρεπει να αποδειξεις οτι xf(x)>f'(x) αρκει να πονηρευτεις το δευτερο μελος.δεν ξερω με την κουραση ολου του διαγωνισματος αν καποιος θα το σκεφτει γρηγορα αυτο!
Αυτόματη ένωση συνεχόμενων μηνυμάτων:
διαφωνω οτι ηταν γελοια θεματα οπως λετε!αν πεφτανε σε κανονικες θα κλαιγανε αρκετοι!το δ3 ναι ειναι δουλεμενο θεμα και το θυμαμαι απλα για καποιον περιεργο λογο σε αυτη τη μορφη δεν το εχουν βαλει ποτε.βαζω στοιχημα οτι αρκετοι θα κολωνανε.επισης,το δ4 ειναι αρκετα πονηρο ερωτημα αν δεν σου ερθει αμεσως.θελει να βλεπεις.επισης,η χ^χ δεν ειναι η πιο γελοια συναρτηση.εχει καποιες παγιδες πχ να απορριψεις το ακρο στο κρισιμο σημειο.ακομα και στο β το β4 δεν ειναι και το πιο συνηθες ερωτημα σε πανελλαδικες που διακρινει μια γνωση.στο γ θεμα το γ4 και αυτο ειναι ωραιο ερωτημα που δεν ειναι αστειο αν δεν εισαι αριστος.
δεν καταλαβαινω γτ τετοια απαξιωση στα θεματα.δηλαδη τι θεματα θελετε?
Όσον αφορά το δ3 τώρα (που μόνο δ3 δεν είναι, το πολύ β), προκύπτει άμεσα από το σύνολο τιμών, δε βλέπω τον λόγο κάποιος να κώλωνε όπως λες.
Και στο δ4, αυτή η διαφορά στο τέλος δε βγάζει μάτια για το ποια συνάρτηση είναι μέσα στο ολοκλήρωμα; Εχεις βρει και την παράγωγο από προηγούμενα ερωτήματα και το βγάζεις κατευθείαν.
εκεί που θα συμφωνήσω είναι στο γ4 που μπορεί κάποιου να μην του 'ρθει εκείνη την ώρα, αλλά και πάλι για να ζητάει κυρτότητα- εφαπτομένη αναγκαστικά με αυτό θα παίξει
Guest 586541
Επισκέπτης
αυτή τη στιγμή δεν είναι συνδεδεμέν. Δεν έχει γράψει κανένα μήνυμα.

13-09-22

19:31
Στοιχειώδη παρατηρητικότητα, άντε και σχετικά καλές αλγεβρικές δεξιότητες απαιτούσε το Δ4...το Δ3 είναι παιδικό, αφού κάθε βόθημα περιέχει όμοιά του..δεν βλέπω τι το περίεργο έχουν τα Β και Γ για σοβαρούς μαθητές, φροντιστηριακότατα...διαφωνω καθετως και οριζοντιως.θεμα σαν το δ4 δεν υπηρχε το καλοκαιρι.πολυ πιο δυσκολα θεματα συνολικα.
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.928 μηνύματα.

13-09-22

20:07
κοροιδευεις το ερωτημα αλλα κανεις ενα πολυ σοβαρο λαθος.οχι ιδιο τυπο αλλα f(x)=g(x).μπορω να σου βαλω 2 συναρτησεις με διαφορετικους τυπους που δινουν ιδια συναρτησιακη τιμη.υπερβολές. Ποια γνώση ακριβώς, το οτι ίσες συναρτήσεις λέγονται αυτές που έχουν ίδιο (τύπο) και πεδίο ορισμού; σιγά το πράγμα. Επίσης θεωρώ δεδομένο ότι ένας μαθητής της γ γνωρίζει ποια σημεία λέγονται κρίσιμα.
Όσον αφορά το δ3 τώρα (που μόνο δ3 δεν είναι, το πολύ β), προκύπτει άμεσα από το σύνολο τιμών, δε βλέπω τον λόγο κάποιος να κώλωνε όπως λες.
Στο δ4, αυτή η διαφορά στο τέλος δε βγάζει μάτια για το ποια συνάρτηση είναι μέσα στο ολοκλήρωμα; Εχεις βρει και την παράγωγο από προηγούμενα ερωτήματα και το βγάζεις κατευθείαν.
εκεί που θα συμφωνήσω είναι στο γ4 που μπορεί κάποιου να μην του 'ρθει εκείνη την ώρα, αλλά και πάλι για να ζητάει κυρτότητα- εφαπτομένη αναγκαστικά με αυτό θα παίξει
Cade
Πολύ δραστήριο μέλος
Ο Cade αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Απόφοιτος λυκείου. Έχει γράψει 856 μηνύματα.

13-09-22

20:09
Για αυτό το έβαλα σε παρένθεση, το γνωρίζω.κοροιδευεις το ερωτημα αλλα κανεις ενα πολυ σοβαρο λαθος.οχι ιδιο τυπο αλλα f(x)=g(x).μπορω να σου βαλω 2 συναρτησεις με διαφορετικους τυπους που δινουν ιδια συναρτησιακη τιμη
πάντως για να κλείνω, αυτό που ήθελα προσωπικά είναι καλύτερα ερωτήματα στο Δ. έστω και ένα που να εξετάζει φαντασία και κριτική σκέψη και όχι παλι χιλιοδουλεμένα ερωτήματα
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.928 μηνύματα.

13-09-22

20:11
τεσπα εγω δεν ειπα οτι ειναι παλουκια αλυτα απλα ειχαν καποια ωραια ερωτηματα.οτι στοιχημα θελετε οτι αν πεφτανε τετοιου τυπου ερωτηματα τον ιουνιο τα ποσοστα αποτυχιας θα ηταν ακομα μεγαλυτερα.εσεις απλα ειστε αριστοι που οτι και αν βαλουν θεματα τα λυνετε.δεν εχει αξια η γνωμη σας.δεν εχουν ολοι την ναυλα τη δικη μας να λυνουν θεματα.επισης,το δ3 που κοροιδευετε ναι συμφωνω ειναι φροντιστηριακο ερωτημα αλλα για καποιον περιεργο λογο δεν εχει πεσει ποτε!οποτε,μπορει πολλοι να μην το ειχανε κανει και να ζοριζονταν.
οσον αφορα το δευτερο θεμα δεν θυμαμαι στο αντιστοιχο δευτερο θεμα του ιουνιου να ηταν μεγαλυτερης δυσκολιας.ισα,ισα εδω ειχε καποια μεγαλυτερη πονηραδα με το πεδιο ορισμου.
Αυτόματη ένωση συνεχόμενων μηνυμάτων:
οσον αφορα το δευτερο θεμα δεν θυμαμαι στο αντιστοιχο δευτερο θεμα του ιουνιου να ηταν μεγαλυτερης δυσκολιας.ισα,ισα εδω ειχε καποια μεγαλυτερη πονηραδα με το πεδιο ορισμου.
hl_amhxanos
Πολύ δραστήριο μέλος
Ο Νίκος Κούκος αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 25 ετών, Απόφοιτος λυκείου και μας γράφει από Αγία Παρασκευή (Αττική). Έχει γράψει 820 μηνύματα.

13-09-22

20:29
Συμφωνώ με Ευκλείδη, εσείς οι 2 έχετε λύσει πολλές ασκήσεις συγκρητικά με ακόμα και το τοπ25% των πανελληνιομάχων βέβαια αυτό μόνο θετικό είναι για εσάς
asdfqwerty
Πολύ δραστήριο μέλος
Ο asdfqwerty αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Φοιτητής του τμήματος Πληροφορικής & Τηλεπικοινωνιών ΕΚΠΑ. Έχει γράψει 1.347 μηνύματα.

13-09-22

20:41
Γιεπ, γενικοτερα αυτο λειπει απο καποια διαγωνισματα πανελληνιων .. καποιο πρωτοτυπο ερωτημα περα απο τα γνωστα και περα απο τα φροντιστηριακα που να βγαζει τον υποψηφιο στα ανοιχτα.. Δεν χρειαζεται να ειναι καποιο τερας .. και κατι μικρο μπορει να κανει την διαφορα γιατι ξεχωριζει την κριτικη σκεψη του υποψηφιου και τι αποκομισε τελικα.Δεν έπεσε κάποιο πρωτότυπο ερώτημα, όπως το φετινό Δ3, το Δ4 του 2019, το Δ3 του 2018, το Δ5 του 2017, κλπ...αναφέρομαι στις κανονικές, ενώ και στις επαναληπτικές έθεταν τέτοιου είδους ερωτήματα...
Cade
Πολύ δραστήριο μέλος
Ο Cade αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Απόφοιτος λυκείου. Έχει γράψει 856 μηνύματα.

15-09-22

01:58
από imc. Η γενική ιδέα είναι απλή, αλλά η λύση όχι και τόσο.

asdfqwerty
Πολύ δραστήριο μέλος
Ο asdfqwerty αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Φοιτητής του τμήματος Πληροφορικής & Τηλεπικοινωνιών ΕΚΠΑ. Έχει γράψει 1.347 μηνύματα.

15-09-22

05:32
θες καταλληλη αρχικη... το f(x) != 0 να σας πονηρεψει.. πρεπει στην τελικη μορφη να υπαρχει ως παρονομαστηςαπό imc. Η γενική ιδέα είναι απλή, αλλά η λύση όχι και τόσο.
View attachment 108517

Cade
Πολύ δραστήριο μέλος
Ο Cade αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Απόφοιτος λυκείου. Έχει γράψει 856 μηνύματα.

10-04-23

11:56
Μια που πλησιάζει ο καιρός είπα να ξαναζωντανεψω το θρεντ με μια απλή άσκηση για τους υποψηφίους.
Λοιπόν, έστω η συνεχής συνάρτηση :
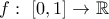
για την οποία ισχύει:
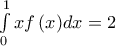
Να δειχθεί ότι :
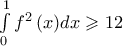
Λοιπόν, έστω η συνεχής συνάρτηση :
για την οποία ισχύει:
Να δειχθεί ότι :
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 2 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 288 μέλη διάβασαν αυτό το θέμα:
- trifasikodiavasma
- ggl
- ioanna2007
- Hased Babis
- thepigod762
- akis_95
- Mariosm.
- Maynard
- infection54
- Jesse_
- topg
- eukleidhs1821
- bill09876
- Debugging_Demon
- mali
- Joji
- Ness
- Helen06
- Scandal
- synthnightingale
- arko
- BillyTheKid
- Magigi
- Paragontas7000
- Unboxholics
- just some guy
- george777
- Wonderkid
- IceCream05
- Abiogenesis
- GeorgePap2003
- katia.m
- giannhs2001
- paul
- Praxis
- Apocalypse
- shezza94
- desp1naa
- rempelos42
- Sherlockina
- oups
- Dimgeb
- spring day
- KingOfPop
- mpapa
- Chrisa
- Physicsstudent
- tsiobieman
- P.Dam.
- persi
- theodoraooo
- PanosBat
- kost28
- mikriarchitectonissa
- BILL KEXA
- Dr. Gl. Luminous
- Eleftheria2
- Athens2002
- bruh_234
- Miranda32
- SlimShady
- kallikd
- nucomer
- alpha.kappa
- Eeeee
- J.Cameron
- Marple
- Kitana
- F1L1PAS
- sophiaa
- VFD59
- papa2g
- το κοριτσι του μαη
- srg96
- Hopeful22
- Φινεύς
- Phys39
- Anta2004
- fairyelly
- Pharmacist01
- jYanniss
- Panagiotis849
- Kokro
- augustine
- Nikoletaant
- Mashiro@Iberan
- margik
- Mammy Nun
- Pastramis
- Σωτηρία
- Appolon
- panosveki
- Nickt23
- igeorgeoikonomo
- Steliosgkougkou
- QWERTY23
- Ameliak
- aladdin
- nimbus
- Φωτεινη Τζα.
- marian
- Georgekk
- xrisamikol
- the purge
- Theodora03
- Machris
- s93060
- Nikitas18
- Stif6
- stav.mdp
- damn
- aekaras 21
- Anthropaki
- Angelos12345
- ioannam
- Μάρκος Βασίλης
- skyway
- Nick2325
- Nala
- Manolo165
- Ryuzaki
- T C
- Devilshjoker
- El_
- George9989
- TonyMontanaEse
- globglogabgalab
- constansn
- barkos
- katerinavld
- fenia
- An_uknown_world
- Jimmis18
- maria2001
- KingPoul
- Xara
- thecrazycretan
- abcdefg12345
- Κλημεντίνη
- ale
- panagiotis G
- mechaniceng
- Giii
- calliope
- Tequila
- natalix
- Cortes
- Alexecon1991
- pepsoula
- Mariaathens
- Lia 2006
- 1205
- παιδι για κλαματα
- Alexandros36k
- alexd99
- chembam
- Specon
- Dr House
- panagiotis23
- Johnman97
- rhymeasylum
- Αννα Τσιτα
- KaterinaL
- Libertus
- LeoDel
- iminspain
- den antexw allh apotyxia
- Λαμπρινηη
- Mendel2003
- Ijt
- drosos
- Κορώνα
- JohnGreek
- Αρχηγος_β3
- alexandra_
- ΘανάσοςG4
- Dimitris9
- Birtjan
- george7cr7
- NickT
- Bgpanos
- JKTHEMAN
- nicole1982
- χημεια4λαιφ
- Stroka
- Kostakis45
- charmander
- leo41
- EiriniS20
- Αριάνα123
- MarilynSt
- iManosX13
- Nefh_
- Viedo
- Βλα
- suaimhneas
- george pol
- kristinbacktoschool
- fearless
- Rene2004
- Steffie88
- Slytherin
- jimnikol21
- Unseen skygge
- cel123
- jul25
- Thanos_D
- Ireneeneri
- tasost
- Mukumbura
- xxxtolis
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki

