BaSO4
Δραστήριο μέλος
Η Δρ. Βουλίδης αυτή τη στιγμή δεν είναι συνδεδεμένη. Είναι Φοιτήτρια του τμήματος Μηχανολόγων Μηχανικών ΑΠΘ. Έχει γράψει 744 μηνύματα.

19-08-22

13:22
Μακάρι να έβρισκα το forum νωρίτερα.Χαίρομαι να βλέπω νέα παιδιά να ασχολούνται με την επίλυση ασκήσεων στα μαθηματικά ενώ οι πανελλήνιες είναι παρελθόν. Αυτό δείχνει ότι τα αγαπήσατε, κατά κάποιο τρόπο. Κι εγώ πριν κάποια χρόνια, έκανα το ίδιο και μου θυμίσατε αυτή την εποχή, σας ευχαριστώ.
Μπράβο σας!

asdfqwerty
Πολύ δραστήριο μέλος
Ο asdfqwerty αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Φοιτητής του τμήματος Πληροφορικής & Τηλεπικοινωνιών ΕΚΠΑ. Έχει γράψει 1.347 μηνύματα.

19-08-22

14:01
βατη ασκηση με γνωστες ιδεες, ειδικα το α) ε @eukleidhs1821View attachment 107005
Τη βρήκα στο ίντερνετ και μου κέντρισε το ενδιαφέρον...δεν ξέρω τι επιφυλάσσει, πάντως είναι ψαρωτική

Το Δ2 (ιιι) παει να δειξει κατι καλο, που υπαρχει αναγκη να κοιταμε οταν λυνουμε εξισωσεις - ανισωσεις.. διοτι ξεχνιεται μιας και στις πανελληνιες δινεται παντα, τωρα βεβαια το εχει προδωσει αρκετα η εκφωνηση.
Και το Δ3 ειναι ενδιαφερον να δει καποιος , μιας και ακολουθεις μια αντιστροφη διαδικασια αποτελεσμα ολοκληρωματος => ολοκληρωμα απο οπου προερχεται το ολοκληρωμα ωστε να καταλαβεις την λυση.
BaSO4
Δραστήριο μέλος
Η Δρ. Βουλίδης αυτή τη στιγμή δεν είναι συνδεδεμένη. Είναι Φοιτήτρια του τμήματος Μηχανολόγων Μηχανικών ΑΠΘ. Έχει γράψει 744 μηνύματα.

19-08-22

14:19
Παίζει να κάνω λάθος, αλλά στο Δ2.iii), εφόσον αυτά μέσα στην h πρέπει να είναι μεγαλύτερα του 0, το πεδίο ορισμού για την εξίσωση δε βγαίνει κενό (x>1 και x<1);View attachment 107005
Τη βρήκα στο ίντερνετ και μου κέντρισε το ενδιαφέρον...δεν ξέρω τι επιφυλάσσει, πάντως είναι ψαρωτική
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.928 μηνύματα.

19-08-22

16:56
ειδες ομως μετα απο τοσα χρονια αυτη την ιδεα την κυνηγανε?θεωρω θεμα χρονου να τεθει στις πανελληνιες και θα δεις οτι παλι δε θα το λυσουν αρκετοι! αν και γενικως αποφευγουν τα τελευταια χρονια ασκησεις τυπου βρειτε τον τυπο της fβατη ασκηση με γνωστες ιδεες, ειδικα το α) ε @eukleidhs1821
Το Δ2 (ιιι) παει να δειξει κατι καλο, που υπαρχει αναγκη να κοιταμε οταν λυνουμε εξισωσεις - ανισωσεις.. διοτι ξεχνιεται μιας και στις πανελληνιες δινεται παντα, τωρα βεβαια το εχει προδωσει αρκετα η εκφωνηση.
Και το Δ3 ειναι ενδιαφερον να δει καποιος , μιας και ακολουθεις μια αντιστροφη διαδικασια αποτελεσμα ολοκληρωματος => ολοκληρωμα απο οπου προερχεται το ολοκληρωμα ωστε να καταλαβεις την λυση.
BaSO4
Δραστήριο μέλος
Η Δρ. Βουλίδης αυτή τη στιγμή δεν είναι συνδεδεμένη. Είναι Φοιτήτρια του τμήματος Μηχανολόγων Μηχανικών ΑΠΘ. Έχει γράψει 744 μηνύματα.

28-08-22

17:59
Ήθελα να ανεβάσω αυτά που έγραψα πιο νωρίς, αλλά το ξέχασα και μετά δεν είχα χρόνο.View attachment 107005
Τη βρήκα στο ίντερνετ και μου κέντρισε το ενδιαφέρον...δεν ξέρω τι επιφυλάσσει, πάντως είναι ψαρωτική


(έχει περικοπεί αρκετά η εικόνα και δε φαίνεται στο τέλος πού τείνει το x)
Cade
Πολύ δραστήριο μέλος
Ο Cade αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Απόφοιτος λυκείου. Έχει γράψει 856 μηνύματα.

28-08-22

18:59
Δεν κατάλαβα στο Δ4 από πού προέκυψε το 6.Ήθελα να ανεβάσω αυτά που έγραψα πιο νωρίς, αλλά το ξέχασα και μετά δεν είχα χρόνο.
για τη g η αιτιολόγηση στο τέλος θα μπορούσε να είναι καλύτερη νομίζω…
Για το Δ2.iii) όπως έχω πει πιο πάνω, ίσως υπάρχει κάποιο ορθογραφικό, γιατί αλλιώς μου φαίνεται πολύ σύντομη η απάντηση…Πάντως, υπάρχει μοτίβο και κάτι ίσως μπορεί να γίνει, αν θέσουμε φ(x)=h(x+2)+h(x), x>0 και χρησιμοποιήσουμε τη μονοτονία/1-1.
Επίσης, ωραίο το Δ3, αν και λίγο προφανές.
Στο Δ4 παίζει να έχω κάνει ορθογραφικά…
(έχει περικοπεί αρκετά η εικόνα και δε φαίνεται στο τέλος πού τείνει το x)
Σωστή πάντως, μπράβο!

* Επίσης το Δ2iii) έτσι πρέπει να βγαίνει γτ έτσι όπως βλέπω τη φ(x) δεν τη κόβω για 1-1
Guest 831328
Επισκέπτης
αυτή τη στιγμή δεν είναι συνδεδεμέν. Δεν έχει γράψει κανένα μήνυμα.

28-08-22

19:27
Αυτές τις ασκήσεις που τις βρίσκειςΔεν κατάλαβα στο Δ4 από πού προέκυψε το 6.
Σωστή πάντως, μπράβο!
* Επίσης το Δ2iii) έτσι πρέπει να βγαίνει γτ έτσι όπως βλέπω τη φ(x) δεν τη κόβω για 1-1
Cade
Πολύ δραστήριο μέλος
Ο Cade αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Απόφοιτος λυκείου. Έχει γράψει 856 μηνύματα.

28-08-22

19:34
Παλιά διαγωνίσματα σχολείων/φροντιστηρίων, βοηθήματα και mathematicaΑυτές τις ασκήσεις που τις βρίσκεις
BaSO4
Δραστήριο μέλος
Η Δρ. Βουλίδης αυτή τη στιγμή δεν είναι συνδεδεμένη. Είναι Φοιτήτρια του τμήματος Μηχανολόγων Μηχανικών ΑΠΘ. Έχει γράψει 744 μηνύματα.

28-08-22

20:05
Στην αρχή στο Ι(α) υπάρχει ο όρος 2(3(α-1)) που βγαίνει 6α-6 και το -6 το βγάζω έξω από το όριο, γιατί είναι σταθερός αριθμός. Πρακτικά, το έκανα, για να με διευκολύνει λιγουλάκι.Δεν κατάλαβα στο Δ4 από πού προέκυψε το 6.
Ούτε κι εμένα μου φαίνεται για 1-1 η φ στο (0,+00)…Αν όντως βγαίνει κενό, μου φαίνεται λίγο βλακεία, παρόλο που ειναι κι αυτό μια απάντηση.Επίσης το Δ2iii) έτσι πρέπει να βγαίνει γτ έτσι όπως βλέπω τη φ(x) δεν τη κόβω για 1-1
asdfqwerty
Πολύ δραστήριο μέλος
Ο asdfqwerty αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Φοιτητής του τμήματος Πληροφορικής & Τηλεπικοινωνιών ΕΚΠΑ. Έχει γράψει 1.347 μηνύματα.

28-08-22

20:19
Για ποιο λογο ειναι βλακεια.. πολλοι ξεχνανε να ορισουν μια εξισωση - ανισωση και ξεκινανε αμεσως την επιλυση. Πολυ ευκολα βλεπεις οτι δεν οριζεται η συγκεκριμενη οποτε η απαντηση ειναι μονοσημαντη. Αυτο θεωρω ηθελε να θυμισει ο θεματοδοτης και φαινεται και απο τον τροπο που το εχει γραψει το ερωτημαΣτην αρχή στο Ι(α) υπάρχει ο όρος 2(3(α-1)) που βγαίνει 6α-6 και το -6 το βγάζω έξω από το όριο, γιατί είναι σταθερός αριθμός. Πρακτικά, το έκανα, για να με διευκολύνει λιγουλάκι.
Ούτε κι εμένα μου φαίνεται για 1-1 η φ στο (0,+00)…Αν όντως βγαίνει κενό, μου φαίνεται λίγο βλακεία, παρόλο που ειναι κι αυτό μια απάντηση.
BaSO4
Δραστήριο μέλος
Η Δρ. Βουλίδης αυτή τη στιγμή δεν είναι συνδεδεμένη. Είναι Φοιτήτρια του τμήματος Μηχανολόγων Μηχανικών ΑΠΘ. Έχει γράψει 744 μηνύματα.

28-08-22

20:21
Απλώς φαίνεται πιο promising από ότι είναι και ξενέρωσα λίγο…Για ποιο λογο ειναι βλακεια.. πολλοι ξεχνανε να ορισουν μια εξισωση - ανισωση και ξεκινανε αμεσως την επιλυση. Πολυ ευκολα βλεπεις οτι δεν οριζεται η συγκεκριμενη οποτε η απαντηση ειναι μονοσημαντη. Αυτο θεωρω ηθελε να θυμισει ο θεματοδοτης και φαινεται και απο τον τροπο που το εχει γραψει το ερωτημα

Cade
Πολύ δραστήριο μέλος
Ο Cade αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Απόφοιτος λυκείου. Έχει γράψει 856 μηνύματα.

28-08-22

20:28
Η αλήθεια είναι αυτήΑπλώς φαίνεται πιο promising από ότι είναι και ξενέρωσα λίγο…

Αυτόματη ένωση συνεχόμενων μηνυμάτων:
Το 2 δε πάει και στους τρεις όρους ;Στην αρχή στο Ι(α) υπάρχει ο όρος 2(3(α-1)) που βγαίνει 6α-6 και το -6 το βγάζω έξω από το όριο, γιατί είναι σταθερός αριθμός. Πρακτικά, το έκανα, για να με διευκολύνει λιγουλάκι.
BaSO4
Δραστήριο μέλος
Η Δρ. Βουλίδης αυτή τη στιγμή δεν είναι συνδεδεμένη. Είναι Φοιτήτρια του τμήματος Μηχανολόγων Μηχανικών ΑΠΘ. Έχει γράψει 744 μηνύματα.

28-08-22

20:33
Ναι, επειδή έβγαλα μόνο το -1 από το όριο, πρέπει αυτό να πολλαπλασιαστεί και με το 2 και με το 3, οπότε βγαίνει -6, ενώ το 2 πάει σε όλο το υπόλοιπο όριο και το 3 πάει μόνο στο α που είναι στην αρχή. Μάλλον έχω κάνει κάποιο μπέρδεμα εκεί, αλλά ακόμη δεν το έχω δει...Το 2 δε πάει και στους τρεις όρους ;
Cade
Πολύ δραστήριο μέλος
Ο Cade αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Απόφοιτος λυκείου. Έχει γράψει 856 μηνύματα.

28-08-22

21:20
Έχεις δίκιο, μόλις το είδα...όλα καλά. Συγχώρεσε με γιατί είμαι κ άυπνος.Ναι, επειδή έβγαλα μόνο το -1 από το όριο, πρέπει αυτό να πολλαπλασιαστεί και με το 2 και με το 3, οπότε βγαίνει -6, ενώ το 2 πάει σε όλο το υπόλοιπο όριο και το 3 πάει μόνο στο α που είναι στην αρχή. Μάλλον έχω κάνει κάποιο μπέρδεμα εκεί, αλλά ακόμη δεν το έχω δει...
Cade
Πολύ δραστήριο μέλος
Ο Cade αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Απόφοιτος λυκείου. Έχει γράψει 856 μηνύματα.

30-08-22

00:40
Μια ωραία
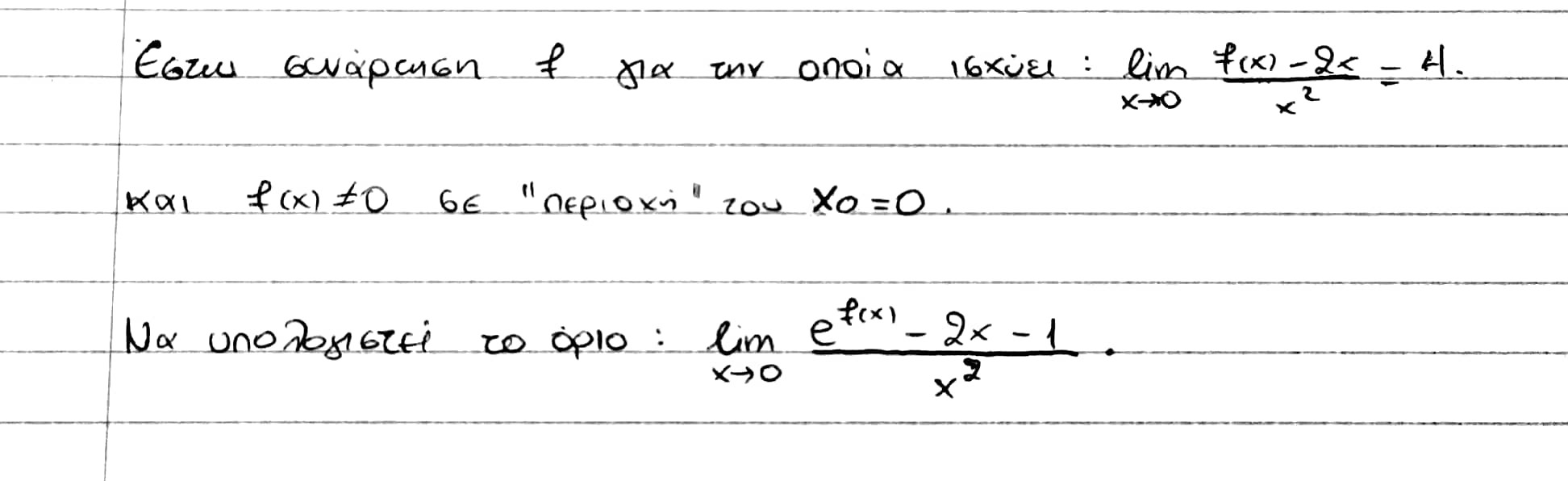
BaSO4
Δραστήριο μέλος
Η Δρ. Βουλίδης αυτή τη στιγμή δεν είναι συνδεδεμένη. Είναι Φοιτήτρια του τμήματος Μηχανολόγων Μηχανικών ΑΠΘ. Έχει γράψει 744 μηνύματα.

30-08-22

00:41
Α ωραία, μικρούλα είναι.Μια ωραία
View attachment 107475
Cade
Πολύ δραστήριο μέλος
Ο Cade αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Απόφοιτος λυκείου. Έχει γράψει 856 μηνύματα.

30-08-22

02:06
Θυμάμαι που προσπαθούσα να τη λύσω πέρυσι τον Αύγουστο στα θερινά και μου χε βγάλει την παναγία. Μιλάμε για ώρεςΑ ωραία, μικρούλα είναι.
Apocalypse
Νεοφερμένο μέλος
Ο Apocalypse αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Μαθητής Γ' λυκείου. Έχει γράψει 24 μηνύματα.

30-08-22

11:36
Τελικά πόσο κάνει το όριο;Μια ωραία
View attachment 107475
Guest 749981
Επισκέπτης
αυτή τη στιγμή δεν είναι συνδεδεμέν. Δεν έχει γράψει κανένα μήνυμα.

30-08-22

12:48
Από την πρώτη ισότητα προκύπτει ότι:
lim f(x) = 0, x -> 0
Έπειτα το ζητούμενο όριο γίνεται με προσθαφαίρεση του f(x) στον αριθμητή
lim(e^f(x) + f(x) - 2x - 1 - f(x))/x²
lim(e^f(x) - f(x) - 1)/x² = L
Είναι f(x) ≠ 0 κοντά στο 0 και υπάρχει η γνωστή ανισότητα e^u - u - 1 >= 0 με την ισότητα στο u = 0. Το όριο γράφεται ως:
lim(e^f(x) - f(x) - 1)* 1/x² = άπειρο,
Το όριο της e^f(x) - f(x) - 1 υπάρχει επειδή υπάρχει της f(x)
lim f(x) = 0, x -> 0
Έπειτα το ζητούμενο όριο γίνεται με προσθαφαίρεση του f(x) στον αριθμητή
lim(e^f(x) + f(x) - 2x - 1 - f(x))/x²
lim(e^f(x) - f(x) - 1)/x² = L
Είναι f(x) ≠ 0 κοντά στο 0 και υπάρχει η γνωστή ανισότητα e^u - u - 1 >= 0 με την ισότητα στο u = 0. Το όριο γράφεται ως:
lim(e^f(x) - f(x) - 1)* 1/x² = άπειρο,
Το όριο της e^f(x) - f(x) - 1 υπάρχει επειδή υπάρχει της f(x)
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 26 ετών, Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11.416 μηνύματα.

30-08-22

13:33
lim [e^f(x) - 2x - 1]/x² =Μια ωραία
View attachment 107475
x->0
lim [e^f(x) - f(x) + f(x) - 2x - 1]/x² =
x->0
lim [e^f(x) - f(x) - 1]/x² + lim[f(x) - 2x]/x² =
x->0
lim [e^f(x) - f(x) - 1]/x² + 4
x->0
Ισχύει πως για κάθε x E R :
e^x >= x+1
e^x - x - 1 >= 0
Η ισότητα ισχύει μόνο όταν x = 0.
Με αντικατάσταση του x με f(x) παραπάνω έχουμε :
e^f(x) - f(x) - 1 >= 0
Κοντά στο 0 η f != 0, οπότε :
lim e^f(x) - f(x) - 1 > 0
x->0
Επομένως :
lim [e^f(x) - f(x) - 1]/x² = κ/0+ = +οο , όπου κ κάποιος πεπερασμένος θετικός αριθμός.
x->0
Έτσι και το αρχικό όριο ισούται με +οο.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 21 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 288 μέλη διάβασαν αυτό το θέμα:
- trifasikodiavasma
- ggl
- ioanna2007
- Hased Babis
- thepigod762
- akis_95
- Mariosm.
- Maynard
- infection54
- Jesse_
- topg
- eukleidhs1821
- bill09876
- Debugging_Demon
- mali
- Joji
- Ness
- Helen06
- Scandal
- synthnightingale
- arko
- BillyTheKid
- Magigi
- Paragontas7000
- Unboxholics
- just some guy
- george777
- Wonderkid
- IceCream05
- Abiogenesis
- GeorgePap2003
- katia.m
- giannhs2001
- paul
- Praxis
- Apocalypse
- shezza94
- desp1naa
- rempelos42
- Sherlockina
- oups
- Dimgeb
- spring day
- KingOfPop
- mpapa
- Chrisa
- Physicsstudent
- tsiobieman
- P.Dam.
- persi
- theodoraooo
- PanosBat
- kost28
- mikriarchitectonissa
- BILL KEXA
- Dr. Gl. Luminous
- Eleftheria2
- Athens2002
- bruh_234
- Miranda32
- SlimShady
- kallikd
- nucomer
- alpha.kappa
- Eeeee
- J.Cameron
- Marple
- Kitana
- F1L1PAS
- sophiaa
- VFD59
- papa2g
- το κοριτσι του μαη
- srg96
- Hopeful22
- Φινεύς
- Phys39
- Anta2004
- fairyelly
- Pharmacist01
- jYanniss
- Panagiotis849
- Kokro
- augustine
- Nikoletaant
- Mashiro@Iberan
- margik
- Mammy Nun
- Pastramis
- Σωτηρία
- Appolon
- panosveki
- Nickt23
- igeorgeoikonomo
- Steliosgkougkou
- QWERTY23
- Ameliak
- aladdin
- nimbus
- Φωτεινη Τζα.
- marian
- Georgekk
- xrisamikol
- the purge
- Theodora03
- Machris
- s93060
- Nikitas18
- Stif6
- stav.mdp
- damn
- aekaras 21
- Anthropaki
- Angelos12345
- ioannam
- Μάρκος Βασίλης
- skyway
- Nick2325
- Nala
- Manolo165
- Ryuzaki
- T C
- Devilshjoker
- El_
- George9989
- TonyMontanaEse
- globglogabgalab
- constansn
- barkos
- katerinavld
- fenia
- An_uknown_world
- Jimmis18
- maria2001
- KingPoul
- Xara
- thecrazycretan
- abcdefg12345
- Κλημεντίνη
- ale
- panagiotis G
- mechaniceng
- Giii
- calliope
- Tequila
- natalix
- Cortes
- Alexecon1991
- pepsoula
- Mariaathens
- Lia 2006
- 1205
- παιδι για κλαματα
- Alexandros36k
- alexd99
- chembam
- Specon
- Dr House
- panagiotis23
- Johnman97
- rhymeasylum
- Αννα Τσιτα
- KaterinaL
- Libertus
- LeoDel
- iminspain
- den antexw allh apotyxia
- Λαμπρινηη
- Mendel2003
- Ijt
- drosos
- Κορώνα
- JohnGreek
- Αρχηγος_β3
- alexandra_
- ΘανάσοςG4
- Dimitris9
- Birtjan
- george7cr7
- NickT
- Bgpanos
- JKTHEMAN
- nicole1982
- χημεια4λαιφ
- Stroka
- Kostakis45
- charmander
- leo41
- EiriniS20
- Αριάνα123
- MarilynSt
- iManosX13
- Nefh_
- Viedo
- Βλα
- suaimhneas
- george pol
- kristinbacktoschool
- fearless
- Rene2004
- Steffie88
- Slytherin
- jimnikol21
- Unseen skygge
- cel123
- jul25
- Thanos_D
- Ireneeneri
- tasost
- Mukumbura
- xxxtolis
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki

