Συλλογή ασκήσεων και τεστ στα Μαθηματικά Προσανατολισμού

[Alexandros28]

Πιο σωστά, το όριο της f στο 0 είναι 1, το οποιο αντί να χρησιμοποιηθεί διπλός τύπος για χ διάφορο του 0 και χ ίσο με 0, καλύπτονται όλες οι τιμές της f αν οριστεί ως η συνχ παντου.

Αυτόματη ένωση συνεχόμενων μηνυμάτων: 30 Ιουλίου 2022

Επίσης υπάρχει η παγιδα και πρέπει να πάρεις περιπτώσεις για χ θετικό και χ αρνητικό λόγω του ότι το θεώρημα ισχύει σε διάστημα και όχι σε ένωση

 

[Cade]

Επίσης υπάρχει η παγιδα και πρέπει να πάρεις περιπτώσεις για χ θετικό και χ αρνητικό λόγω του ότι το θεώρημα ισχύει σε διάστημα και όχι σε ένωση

σίγουρα; επειδή η σχέση xf(x)=xcosx ισχύει για κάθε χ.
για που λες;

 

[Alexandros28]

Διαιρώντας δια χ ισχύει για το R*, μπορούμε όμως να βρουμε το όριο της f στο 0. Και αφού η f είναι συνεχής, η τιμή αυτή ισούται με το f(0)=1=συν0

Αυτόματη ένωση συνεχόμενων μηνυμάτων: 30 Ιουλίου 2022

Καλά άλλο καταλαβα για τις περιπτώσεις, συγχωρα με γιατί είμαι και έξω. Νόμιζα ότι χρειαζόταν να διαιρέσεις με χ πριν λυθεί η διαφορική

 

[Cade]

.

 

[asdfqwerty]

β) Εστω: h(x) = f(x) + x * e^-1 -1 , x στο [0, π / 2]
h'(x) = -ημχ + e^-1
h''(x) = -συνx < 0 => h' φθινουσα

h'(0) = e^-1 > 0
h'(π / 2) = e^-1 - 1 < 0
bolzano .. => υπαρχει μοναδικο x_o στο (0, π / 2) : h'(xo) = 0

h'(x) > 0 (0, x_o) => h γν. αυξουσα στο [0, x_o] με h(0) = 0 => h(x) >= 0 στο [0, x_0]

γ) η εξισωση ειναι αδυνατη για x > 1 μιας και x^2 > 1 >= συνχ

Εστω: φ(χ) = συνχ - χ^2, για χ <= 1
φ'(χ) = -ημχ - 2χ ( μπορει να βγει το προσημο και απο εδω με παραπανω γραψιμο)
φ''(χ) = -συνχ - 2 < 0

( -1 <= -συνχ <= 1 <=> -3 <= -συνχ -2 <= -1 < 0)

φ' γνησιως φθινουσα και παρατηρουμε φ'(0) = 0 μοναδικη ριζα οποτε
εχουμε φ'(χ) >0 για x < 0 και φ'(x) < 0 στο (0,1)

=> φ γν. αυξουσα στο (-οο, 0]
=> φ γν. φθινουσα στο [0, 1]

φ(0) = 1
φ(1) = συν1 - 1 < 0

=> υπαρχει μοναδικο χ_2 στο (0, 1) τ.ω φ(χ_2) = 0

lim(x-> -oo) φ(χ) = χ^2 ( συνχ / χ^2 - 1) = (+οο) (0 - 1) = -00

=> υπαρχει μοναδικο χ_1 στο (-οο, 0) τ.ω φ(χ_1) = 0

δ) συνχ φθινουσα στο [0, π / 2] => g φθινουσα στο [0, π / 2] => g 1-1 => υπαρχει g^-1
με πεδιο ορισμου το [0, 1]

ισχυει: g(g^-1 (x)) = x για καθε χ στο [0, 1]

=> g'(g^-1(x)) * (g^-1)'(x) = 1 (E)

g'(g^-1(x)) = 0 <=> ημg^-1(x) = 0 ( ημ στο [0,1] υποσυνολο του [0, π / 2] ειναι αυξουσα αρα και 1-1)

g^-1(x) = 0 <=> x = 1

=> (g^-1)'(x) = 1 / g'(g^-1(x)) , x στο [0, 1)

ε) g'(x) = 1 / g'(g^-1(x)) , x στο [0, 1)

<=> ημx = 1 / ημ(g^-1(x))

το πρωτο μελος ειναι < 1 ενω το 2ο > 1

οποτε η εξισωση ειναι αδυνατη...

ελπισω να μην εγραψα καμια πατατα γιατι το πηγα μονοκοπανια :p...

 

[eukleidhs1821]

β) Εστω: h(x) = f(x) + x * e^-1 -1 , x στο [0, π / 2]
h'(x) = -ημχ + e^-1
h''(x) = -συνx < 0 => h' φθινουσα

h'(0) = e^-1 > 0
h'(π / 2) = e^-1 - 1 < 0
bolzano .. => υπαρχει μοναδικο x_o στο (0, π / 2) : h'(xo) = 0

h'(x) > 0 (0, x_o) => h γν. αυξουσα στο [0, x_o] με h(0) = 0 => h(x) >= 0 στο [0, x_0]

γ) η εξισωση ειναι αδυνατη για x > 1 μιας και x^2 > 1 >= συνχ

Εστω: φ(χ) = συνχ - χ^2, για χ <= 1
φ'(χ) = -ημχ - 2χ ( μπορει να βγει το προσημο και απο εδω με παραπανω γραψιμο)
φ''(χ) = -συνχ - 2 < 0

( -1 <= -συνχ <= 1 <=> -3 <= -συνχ -2 <= -1 < 0)

φ' γνησιως φθινουσα και παρατηρουμε φ'(0) = 0 μοναδικη ριζα οποτε
εχουμε φ'(χ) >0 για x < 0 και φ'(x) < 0 στο (0,1)

=> φ γν. αυξουσα στο (-οο, 0]
=> φ γν. φθινουσα στο [0, 1]

φ(0) = 1
φ(1) = συν1 - 1 < 0

=> υπαρχει μοναδικο χ_2 στο (0, 1) τ.ω φ(χ_2) = 0

lim(x-> -oo) φ(χ) = χ^2 ( συνχ / χ^2 - 1) = (+οο) (0 - 1) = -00

=> υπαρχει μοναδικο χ_1 στο (-οο, 0) τ.ω φ(χ_1) = 0

δ) συνχ φθινουσα στο [0, π / 2] => g φθινουσα στο [0, π / 2] => g 1-1 => υπαρχει g^-1
με πεδιο ορισμου το [0, 1]

ισχυει: g(g^-1 (x)) = x για καθε χ στο [0, 1]

=> g'(g^-1(x)) * (g^-1)'(x) = 1 (E)

g'(g^-1(x)) = 0 <=> ημg^-1(x) = 0 ( ημ στο [0,1] υποσυνολο του [0, π / 2] ειναι αυξουσα αρα και 1-1)

g^-1(x) = 0 <=> x = 1

=> (g^-1)'(x) = 1 / g'(g^-1(x)) , x στο [0, 1)

ε) g'(x) = 1 / g'(g^-1(x)) , x στο [0, 1)

<=> ημx = 1 / ημ(g^-1(x))

το πρωτο μελος ειναι < 1 ενω το 2ο > 1

οποτε η εξισωση ειναι αδυνατη...

ελπισω να μην εγραψα καμια πατατα γιατι το πηγα μονοκοπανια :p...

νομιζω για να φανει η παραγωγισιμοτητα της αντιστροφης ασχετα αν σου χει λεει εξαρχης οτι ειναι παραγωγισιμη καλυτερα να ξεκιναγες αναποδα απο το f^-1(f(x))=x

 

[Guest 831328]

Εγώ για το ερώτημα δ βρήκα αυτή την λύση, είναι σωστη??

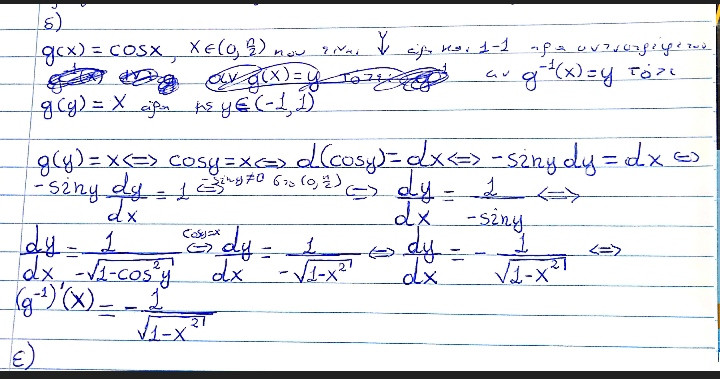
Σόρρυ yε(0,1)

 

[eukleidhs1821]

πρακτικα αν κανεις την διαδικασια που κανε ο asd βγαζεις οτι η παραγωγος της αντιστροφη ισουται με 1/f'(x).Αυτο στη γενικη περιπτωση.
Εδω βγαζεις -1/ημχ θες ομως το ημχ να το εκφρασεις με το συνχ=y επομενως ημχ=τεραγωνικη ριζα(1-συν^2χ)=ριζα (1-y^2) επειδη ειμαστε στο πρωτο τεταρτημοριο.

Αυτόματη ένωση συνεχόμενων μηνυμάτων: 30 Ιουλίου 2022

για το ε) μια εναλλακτικη για να ειναι παραλληλες πρεπει f'(x)=-1/f'(x) δηλαδη καταληγεις ημ^2χ=1 που αυτο εφοσον μιλαμε στο (0,π/2) η εξισωση ειναι αδυνατη.επομενως δεν εχουν παραλληλες εφαπτομενες.αν την οριζε την f στο π/2 τοτε θα ειχανε!

Αυτόματη ένωση συνεχόμενων μηνυμάτων: 30 Ιουλίου 2022

το δευτερο ερωτημα μοιαζει σε πολυ μεγαλο βαθμο με το δ1 των πανελλαδικων του 2020 απλα μπερδεψανε την εκφωνηση εδω.θα μπορουσαν να πουν δειξτε οτι η συναρτηση εχει τοπικο μεγιστο στο χ0 ανηκει στο (0,π/2)

Αυτόματη ένωση συνεχόμενων μηνυμάτων: 30 Ιουλίου 2022

β) Εστω: h(x) = f(x) + x * e^-1 -1 , x στο [0, π / 2]
h'(x) = -ημχ + e^-1
h''(x) = -συνx < 0 => h' φθινουσα

h'(0) = e^-1 > 0
h'(π / 2) = e^-1 - 1 < 0
bolzano .. => υπαρχει μοναδικο x_o στο (0, π / 2) : h'(xo) = 0

h'(x) > 0 (0, x_o) => h γν. αυξουσα στο [0, x_o] με h(0) = 0 => h(x) >= 0 στο [0, x_0]

γ) η εξισωση ειναι αδυνατη για x > 1 μιας και x^2 > 1 >= συνχ

Εστω: φ(χ) = συνχ - χ^2, για χ <= 1
φ'(χ) = -ημχ - 2χ ( μπορει να βγει το προσημο και απο εδω με παραπανω γραψιμο)
φ''(χ) = -συνχ - 2 < 0

( -1 <= -συνχ <= 1 <=> -3 <= -συνχ -2 <= -1 < 0)

φ' γνησιως φθινουσα και παρατηρουμε φ'(0) = 0 μοναδικη ριζα οποτε
εχουμε φ'(χ) >0 για x < 0 και φ'(x) < 0 στο (0,1)

=> φ γν. αυξουσα στο (-οο, 0]
=> φ γν. φθινουσα στο [0, 1]

φ(0) = 1
φ(1) = συν1 - 1 < 0

=> υπαρχει μοναδικο χ_2 στο (0, 1) τ.ω φ(χ_2) = 0

lim(x-> -oo) φ(χ) = χ^2 ( συνχ / χ^2 - 1) = (+οο) (0 - 1) = -00

=> υπαρχει μοναδικο χ_1 στο (-οο, 0) τ.ω φ(χ_1) = 0

δ) συνχ φθινουσα στο [0, π / 2] => g φθινουσα στο [0, π / 2] => g 1-1 => υπαρχει g^-1
με πεδιο ορισμου το [0, 1]

ισχυει: g(g^-1 (x)) = x για καθε χ στο [0, 1]

=> g'(g^-1(x)) * (g^-1)'(x) = 1 (E)

g'(g^-1(x)) = 0 <=> ημg^-1(x) = 0 ( ημ στο [0,1] υποσυνολο του [0, π / 2] ειναι αυξουσα αρα και 1-1)

g^-1(x) = 0 <=> x = 1

=> (g^-1)'(x) = 1 / g'(g^-1(x)) , x στο [0, 1)

ε) g'(x) = 1 / g'(g^-1(x)) , x στο [0, 1)

<=> ημx = 1 / ημ(g^-1(x))

το πρωτο μελος ειναι < 1 ενω το 2ο > 1

οποτε η εξισωση ειναι αδυνατη...

ελπισω να μην εγραψα καμια πατατα γιατι το πηγα μονοκοπανια :p...

γτ δεν εκανες κριτηριο παρεμβολης κατευθειαν και το εκανες ετσι?αφου εβγαινε αμεσως

 

[eukleidhs1821]

Εγώ για το ερώτημα δ βρήκα αυτή την λύση, είναι σωστη??

Σόρρυ yε(0,1)View attachment 105872

αυτο με τα διαφορικα ειναι για τους αμπαλους τους φυσικους που δεν ξερουν μαθηματικα.
καλυτερα καντο οπως ο asd και ξεκινα καλυτερα απο το f^-1(f(x)=x για να το καταλαβεις.
παρεμπιπτοντως αυτους τους τυπους των αντιστροφων τριγωνομετρικων τις παραγωγους τους μαθαινεις απεξω στο πρωτο ετος.
παραγωγος του τοξου εφαπτομενης ειναι 1/1+χ^2.σε βοηθα και στα ολοκληρωματα αυτο.
δηλαδη αν δεις ενα ολοκληρωμα 1/1+χ^2 κατευθειαν λες arc(tanx)+c.

 

[Guest 831328]

αυτο με τα διαφορικα ειναι για τους αμπαλους τους φυσικους που δεν ξερουν μαθηματικα.
καλυτερα καντο οπως ο asd και ξεκινα καλυτερα απο το f^-1(f(x)=x για να το καταλαβεις.
παρεμπιπτοντως αυτους τους τυπους των αντιστροφων τριγωνομετρικων τις παραγωγους τους μαθαινεις απεξω στο πρωτο ετος.
παραγωγος του τοξου εφαπτομενης ειναι 1/1+χ^2.σε βοηθα και στα ολοκληρωματα αυτο.
δηλαδη αν δεις ενα ολοκληρωμα 1/1+χ^2 κατευθειαν λες arc(tanx)+c.

Καλά εγώ από πανελλαδικές έληξα. Πλέον θα αρχίσω τις σπουδές μου στο ceid. Πληροφορικός θα είμαι, οπότε δεν με ενδιαφέρει και τόσο το τυπικό των μαθηματικών πλέον, γιατί αυτό για τους τύπους είναι που λες. Δεν βλέπω τίποτα λανθασμένο στην λογική μου οπότε, as long as it works I will not try to fix it. Επίσης την ίδια απόδειξη που παρέθεσα με τα διαφορικά έχει το σχολικό βιβλίο των μαθηματικών γ λυκείου στην Κύπρο που έχουν εντός ύλης αντίστροφες τριγωνομετρικές.

 

[Alexandros28]

για το ε) μια εναλλακτικη για να ειναι παραλληλες πρεπει f'(x)=-1/f'(x) δηλαδη καταληγεις ημ^2χ=1 που αυτο εφοσον μιλαμε στο (0,π/2) η εξισωση ειναι αδυνατη.επομενως δεν εχουν παραλληλες εφαπτομενες.αν την οριζε την f στο π/2 τοτε θα ειχανε!

Δεν έχω καταλάβει τι εννοείς ακριβώς εδώ, αλλά δε νομίζω να είναι σωστή λογική να ψάξεις κάποιο χ στο οποιο είναι παράλληλες οι εφαπτομενες. Μπορεί να έχουν παράλληλες εφαπτομενες σε διαφορετικό χ, όχι απαραίτητα στο ίδιο. Προτιμότερο θεωρώ είναι να εξετάσουμε τα σύνολα τιμών των δυο συναρτησεων και αν η τομή τους είναι το κενό σύνολο, τότε δεν υπάρχουν παράλληλες εφαπτομενες

 

[hl_amhxanos]

Καλά εγώ από πανελλαδικές έληξα. Πλέον θα αρχίσω τις σπουδές μου στο ceid. Πληροφορικός θα είμαι, οπότε δεν με ενδιαφέρει και τόσο το τυπικό των μαθηματικών πλέον, γιατί αυτό για τους τύπους είναι που λες. Δεν βλέπω τίποτα λανθασμένο στην λογική μου οπότε, as long as it works I will not try to fix it. Επίσης την ίδια απόδειξη που παρέθεσα με τα διαφορικά έχει το σχολικό βιβλίο των μαθηματικών γ λυκείου στην Κύπρο που έχουν εντός ύλης αντίστροφες τριγωνομετρικές.

Σόρρυ που δεν έχω προσδώσω κάτι σχετικό με το νήμα αλλά όταν έγραψες το μήνυμά σου αυτόματα μου πετάχτηκε στο μυαλό αυτό το βίντεο, χαχαχα δεν θα ήθελες να μάθεις να προγραμματίζεις ένα donut με ascii characters ?

 

[Guest 831328]

Σόρρυ που δεν έχω προσδώσω κάτι σχετικό με το νήμα αλλά όταν έγραψες το μήνυμά σου αυτόματα μου πετάχτηκε στο μυαλό αυτό το βίντεο, χαχαχα δεν θα ήθελες να μάθεις να προγραμματίζεις ένα donut με ascii characters ?

Δεν είπα σε καμία περίπτωση ότι δεν θα χρειαστώ μαθηματικά, θά τά χρειαστώ και μου αρέσουν και θέλω να καταπιαστώ με αυτά, αλλά το τυπικό της υπόθεσης των μαθηματικών που πρέπει να έχει έναν συγκεκριμένο τρόπο παρουσίασης στο μαθηματικό κομμάτι με εκνευρίζει λίγο

 

[hl_amhxanos]

Δεν είπα σε καμία περίπτωση ότι δεν θα χρειαστώ μαθηματικά, θά τά χρειαστώ και μου αρέσουν και θέλω να καταπιαστώ με αυτά, αλλά το τυπικό της υπόθεσης των μαθηματικών που πρέπει να έχει έναν συγκεκριμένο τρόπο παρουσίασης στο μαθηματικό κομμάτι με εκνευρίζει λίγο

Συμφωνώ μαζί σου! δεν θα σου κόψει κανείς μονάδες πλέον αν γράψεις την παράγωγο με τον συμβολισμό του Όιλερ αντί του Λανγράνζ, άσε που οι περισσότεροι μαθηματικοί τον δικό σου συμβολισμό προτιμούνε

 

[eukleidhs1821]

Δεν έχω καταλάβει τι εννοείς ακριβώς εδώ, αλλά δε νομίζω να είναι σωστή λογική να ψάξεις κάποιο χ στο οποιο είναι παράλληλες οι εφαπτομενες. Μπορεί να έχουν παράλληλες εφαπτομενες σε διαφορετικό χ, όχι απαραίτητα στο ίδιο. Προτιμότερο θεωρώ είναι να εξετάσουμε τα σύνολα τιμών των δυο συναρτησεων και αν η τομή τους είναι το κενό σύνολο, τότε δεν υπάρχουν παράλληλες εφαπτομενες

ναι εχεις δικιο!μεγαλο λαθος συμβαινει

 

[Cade]

πάμε και άλλη μια

δεν την έχω λύσει ούτε γω ακόμη αλλά είδα τα δεδομένα και μου φάνηκε καλή

 

[eukleidhs1821]

ωραια ασκησουλα.
πρωτο ερωτημα.θετω ολη την παρασταση μεσα στο οριο h(x) που γνωριζω το οριο και λυνω ως προς e^f(x)-1-f(x) ξες e^f(x)-1-f(x)=x^2g(x)
lim(e^f(x)-1-f(x))=0 λογω συνεχειας καταληγεις οτι e^f(0)-1-f(0)=0
ομως e^x>=x+1 για καθε πραγματικο αντικαθιστωντας οπου χ το χ-1 παιρνουμε e^x-1-x>=0 με την ισοτητα να ισχυει μονο για χ=1 επομενως f(0)=1.εκφραστικα ισως μπορουμε να το πουμε καλυτερα.
δευτερο ερωτημα.κανω de l hospital και καταληγω να απομονωσω το εξης
limf'(x) lim(e^f(x)-1-1)/2x το δευτερο οριο ξανακανοντας de l hospital βγαινει f'(0)/2
το πρωτο παλι κανει f'(0) επομενως εχεις f'(0)^2=4 ομως ξες οτι f'(0)<0 λογω αμβλειας γωνιας που λεει αρα f'(0)=-2 εξισωση βγαινει y=-2x+1
τριτο ερωτημα.ειναι f'(x)^2>0 καθαρα θετικο επομενως αν τα ακρα του ολοκληρωματος δεν ειναι ιδια θα βγαινει το ολοκληρωμα ειτε θετικο ειτε αρνητικο.επομενως f(0)=f(1)
με rolle το βρηκες. μετα λογω συνεχειας δευτερας παραγωγου εχεις οτι διατηρει προσημο η δευτερα παραγωγος αφου ειναι διαφορη μηδενος.
κανεις θμτ στο [0,ξ] για την f' και βγαζεις f''(ξ)>0 αρα γενικευεται αυτο και ιεναι κυρτη
τεταρτο ερωτημα.η f' γνησιως αυξουσα και πιανεσαι απο τη μονοτονια γυρω απο το ξ επομενως βγαζεις το ελαχιστο.
πεμπτο ερωτημα στο [1,3] ειναι γνησιως αυξουσα. 1<=χ<=3 f(x)>=f(1) πεφτεις στα ολοκληρωματα ολοκληρωμαf(x)dx>2f(1)=2f(0)=2

 

[Cade]

Δεν την έχω δει, ελπίζω να είναι εντάξει

 

[eukleidhs1821]

View attachment 106489
Δεν την έχω δει, ελπίζω να είναι εντάξει

επρεπε να την ανεβασεις αλλη μερα.σημερα εχω τοση τσαντιλα απο χτες που ακομα δεν εχω συνελθει.θα προσπαθησω ομως να τη δω

 

[Guest 586541]

Δ1 Θέτεις συνάρτηση g(x)=e^x+lnx+x, με παραγώγιση βγαίνει αύξουσα. Από κατασκευαστική το x-2 αύξουσα. (f(x)>0 από περιορισμό) Άρα για x1<x2 προκύπτει g(f(x1))<g(f(x2))<=>f(x1)<f(x2).

Δ2i Αν στην δοσμένη περάσουμε limx->+oo προκύπτει limx->+oo (e^f(x)+lnf(x)+f(x))=+oo

Αν το limx->+oo του f(x) είναι:

- Πραγματικός διάφορος του μηδέν άτοπο, γιατί δεν θα παίρναμε άπειρο.

- Μηδέν άτοπο, γιατί θα παίρναμε -oo.

- +oo Πιθανό γιατί θα παίρναμε +oo.

Επειδή η μόνη δυνατή περίπτωση είναι η τρίτη, θα είναι και η σωστή.

Όμοια σκεφτόμαστε στο -oo και βγαίνει το ζητούμενο.

Και λόγω της μονοτονίας το σύνολο τιμών ισούται με (limx->-oo+,limx->+oo).

Δ2ii Εφόσον f αύξουσα και άρα 1-1 θα αντιστρέφεται. Θέτουμε όπου x το f^-1(x) και προκύπτει.

Δ3i παρατηρούμε ότι h(1)=e+3. Οπότε εμφανίζεται η παράγωγος. Για το h(x-1) με θέσιμο.

Δ3ii Το δεξιά από το > είναι το h(x^2+1). Λόγω μονοτονίας αρκεί e^x>x^2+1 όπου με πέρασμα ln και μετά όλα στα δεξιά, βγαίνει αύξουσα. Αυτό που θέσαμε κάνει 0 μόνο για x=0, άρα για κάθε x>0 ισχύει η ανίσωση.

Δ4 Στα αριστερά το h(a) και ΘΜΤ. Το e+2 ισούται με h'(1) και αφού a>1 λόγω της μονοτονίας προκύπτει.