Θεωρούμε την συνάρτηση
=\max\left\{x^3, \cos^2 x \right\})
.
i) Nα δείξετε ότι υπάρχει μοναδικό
)
τέτοιο ώστε
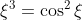
ii) Να δείξετε ότι
= \min f(x))
στο
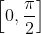
iii) Να βρεθεί το πλήθος των ριζών της εξίσωσης
=\lambda)
για κάθε τιμή της παραμέτρου
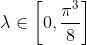
*Το cos δηλώνει το συνημίτονο
Για x>1 είναι x^3>1 και -1<=συνx<=1 => |συνx|<=1 => |συνx|^2<=1 => (συνx)^2<=1
Άρα (συνx)^2<=1<x^3. Επομένως για x>1 είναι f(x)=x^3
Για x<0 είναι x^3<0 και 0<=(συνx)^2<=1.
Άρα x^3<0<=(συνx)^2. Επομένως για x<0 είναι f(x)=(συνx)^2.
Μένει να καθοριστεί ο τύπος της f στο διάστημα [0,1].
Θεωρούμε την συνάρτηση g(x)=(x^3)-((συνx)^2), x ανήκει R. Η g είναι συνεχής και παραγωγίσιμη στο R με πρώτη παράγωγο:
g΄(x)=3(x^2)+ημ2x
Για 0<x<π/2 είναι 0<2x<π και επομένως 0<ημ2x<=1. Επειδή x^2>0 και ημ2x>0 για κάθε x ανήκει (0,π/2) τότε είναι g΄(x)>0 για κάθε x ανήκει (0,π/2). Η g είναι συνεχής στο [0,π/2], παραγωγίσιμη στο (0,π/2) και ισχύει g΄(x)>0 για κάθε x στο (0,π/2). Επομένως η g είναι γνησίως αύξουσα στο [0,π/2].
Έχουμε g(0)=-1<0 και g(π/2)=(π^3)/8>0, οπότε g(0)g(π/2)<0. Η g είναι συνεχής στο [0,π/2] και ισχύει g(0)g(π/2)<0. Επομένως σύμφωνα με το θεώρημα Bolzano υπάρχει ξ ανήκει (0,π/2) τέτοιο ώστε g(ξ)=0 => ξ^3=(συνξ)^2 και επειδή η g είναι γνησίως αύξουσα τότε αυτό είναι μοναδικό.
Επίσης έχουμε g(1)=1-((συν1)^2). Επειδή 0<1<π/3 τότε είναι συν(π/3)<συν1<συν0 => 1/2<συν1<1 => 1/4<(συν1)^2<1 =>
=> -1<-((συν1)^2)<-1/4 => 0<1-((συν1)^2)

/4 => 0<g(1)

/4
Είναι g(0)<0 και g(1)>0. Η g είναι συνεχής στο [0,π/2] και ισχύει g(0)g(1)<0. Επομένως σύμφωνα με το θεώρημα Bolzano υπάρχει x0 ανήκει (0,1) τέτοιο ώστε g(x0)=0 => x0^3=(συνx0)^2 και επειδή η g είναι γνησίως αύξουσα τότε αυτό είναι μοναδικό και ισχύει x0=ξ.
Άρα f(ξ)=ξ^3=(συνξ)^2 όπου 0<ξ<1
Με δεδομένο ότι η g είναι γνησίως αύξουσα στο [0,1] (υποσύνολο του [0,π/2]) έχουμε:
0<=x<ξ => g(x)<g(ξ) => (x^3)-((συνx)^2)<0 => (x^3)<(συνx)^2 => Άρα f(x)= (συνx)^2 για 0<=x<ξ
ξ<x<=1 => g(ξ)<g(x) => 0<(x^3)-((συνx)^2) => (x^3)>(συνx)^2 => Άρα f(x)= x^3 για ξ<x<=1
Συνοψίζοντας
f(x)=(συνx)^2, x<ξ
f(x)=(x^3), x>ξ
f(ξ)=ξ^3=(συνξ)^2
Η συνάρτηση f είναι συνεχής στα διαστήματα (-οο,ξ) και (ξ,+οο). Στο σημείο ξ έχουμε:
lim(x->ξ-)f(x)=lim(x->ξ-)((συνx)^2)=(συνξ)^2=f(ξ)
lim(x->ξ+)f(x)=lim(x->ξ-)(x^3)=ξ^3=f(ξ)
Επειδή lim(x->ξ-)f(x)=lim(x->ξ+)f(x)=f(ξ) τότε η f είναι συνεχής στο ξ. Επομένως η f είναι συνεχής στο R.
Η f είναι παραγωγίσιμη στο (-οο,ξ) με πρώτη παράγωγο f΄(x)=-ημ2x. Για 0<x<ξ<1<π/2 είναι 0<2x<2ξ<2<π, οπότε ημ2x>0 => -ημ2x<0 =>
=> f΄(x)<0 για κάθε x ανήκει (0,ξ).
H f είναι παραγωγίσιμη στο (ξ,+οο) με πρώτη παράγωγο f΄(x)=3(x^2). Για 0<ξ<x είναι x^2>0 => f΄(x)>0.
Άρα f΄(x)>0 για κάθε x στο (ξ, +οο)
Η f είναι συνεχής στο [0,ξ], παραγωγίσιμη στο (0,ξ) και ισχύει f΄(x)<0 για κάθε x στο (0,ξ). Επομένως η f είναι γνησίως φθίνουσα στο [0,ξ].
Η f είναι συνεχής στο [ξ,+οο), παραγωγίσιμη στο (ξ,+οο) και ισχύει f΄(x)<0 για κάθε x στο (ξ,+οο). Επομένως η f είναι γνησίως φθίνουσα στο [ξ,+οο).
Επειδή η f είναι συνεχής στο [0,π/2], γνησίως φθίνουσα στο [0,ξ] και γνησίως αύξουσα στο [ξ,π/2] (ως υποσύνολο του [ξ,+οο)) τότε παρουσιάζει τοπικό ελάχιστο στο ξ με τιμή: minf(x)=f(ξ)
Άρα f(ξ)=minf(x) στο [0,π/2]
Επειδή 0<ξ<1 είναι 0<ξ^3<1 => 0<f(ξ)<1 όπου f(ξ)=ξ^3=(συνξ)^2
Έχουμε lim(x->+oo)f(x)=lim(x->+oo)(x^3)=+oo
Για κάθε x ανήκει (-οο,ξ) είναι f(x)=(συνx)^2 και ισχύει 0<=(συνχ)^2<=1. Επομένως η εικόνα του (-οο,ξ) είναι το f((-oo,ξ))=[0,1]
Επειδή η f είναι συνεχής και γνησίως αύξουσα στο (ξ,+οο) τότε f((ξ,+οο))=(f(ξ),+οο)
Επίσης το 0 είναι ολικό ελάχιστο της f, δηλαδή f(x)>=0 για κάθε x ανήκει R.
Θα αναζητηθούν οι λύσεις της f(x)=λ στο R όπου 0<=λ<=(π^3)/8
(α) Θα αναζητηθούν οι λύσεις της εξίσωσης f(x)=λ στο διάστημα (-οο,ξ) όπου f(x)=(συνx)^2.
(i) Επειδή 0<=(συνx)^2<=1 για κάθε x<ξ τότε για 1<λ<=(π^3)/8 η εξίσωση f(x)=λ δεν έχει λύσεις
(ii) Αν 0<=λ<=1 τότε η εξίσωση (συνx)^2=λ έχει λύσεις. Έστω 0<=φ<=π/2 με συνφ=SQRT(λ). Έχουμε
(συνx)^2=λ => |συνx|=SQRT(λ) => συνx=SQRT(λ) ή συνx=-SQRT(λ) => συνx=συνφ ή συνx=-συνφ =>
=> συνx=συνφ ή συνx=συν(π-φ)
Για συνx=συνφ προκύπτει x=2απ+φ ή x=2βπ-φ όπου α,β ανήκουν Z
Για συνx=συν(π-φ) προκύπτει x=2γπ+π-φ ή x=2δπ-π+φ όπου γ, δ ανήκουν Z
Επειδή x<ξ τότε για τους ακέραιους α, β, γ, δ ισχύουν οι εξής περιορισμοί:
2απ+φ<ξ => α<(ξ-φ)/(2π)
2βπ-φ<ξ => β<(ξ+φ)/(2π)
2γπ+π-φ<ξ => γ<(ξ+φ-π)/(2π)
2δπ-π+φ<ξ => δ<(ξ-φ+π)/(2π)
(β) Θα αναζητηθούν οι λύσεις της εξίσωσης f(x)=λ στο διάστημα [ξ,+οο) όπου f(x)=x^3.
f(x)=λ => x^3=λ => x=λ^(1/3)
Πρέπει x>=ξ => λ^(1/3)>=ξ => λ>=ξ^3 => λ>=f(ξ)
Άρα αν 0<=λ<ξ^3 τότε η εξίσωση f(x)=λ δεν έχει λύσεις στο [ξ,+οο)
Αν ξ^3<λ<=(π^3)/8 τότε έχει μοναδική λύση την x=λ^(1/3)
Συνεπώς καταλήγουμε στα εξής συμπεράσματα:
(α) Αν 0<=λ<ξ^3 τότε τα x=2απ+φ, x=2βπ-φ, x=2γπ+π-φ και x=2δπ-π+φ είναι λύσεις της εξίσωσης f(x)=λ όπου συνφ=λ^(1/2) με 0<=φ<=π/2 και για τους ακεραίους α, β, γ και δ ισχύουν οι περιορισμοί:
α<(ξ-φ)/(2π)
β<(ξ+φ)/(2π)
γ<(ξ+φ-π)/(2π)
δ<(ξ-φ+π)/(2π)
Άρα σε αυτήν την περίπτωση η εξίσωση f(x)=λ έχει άπειρες πραγματικές λύσεις.
(β) Αν ξ^3<=λ<=1 τότε τα x=2απ+φ, x=2βπ-φ, x=2γπ+π-φ, x=2δπ-π+φ και x=λ^(1/3) είναι λύσεις της εξίσωσης f(x)=λ όπου συνφ=λ^(1/2) με 0<=φ<=π/2 και για τους ακεραίους α, β, γ και δ ισχύουν οι περιορισμοί:
α<(ξ-φ)/(2π)
β<(ξ+φ)/(2π)
γ<(ξ+φ-π)/(2π)
δ<(ξ-φ+π)/(2π)
Άρα σε αυτήν την περίπτωση η εξίσωση f(x)=λ έχει άπειρες πραγματικές λύσεις.
(γ) Αν 1<λ<=(π^3)/8 τότε η εξίσωση f(x)=λ έχει μοναδική λύση την x=λ^(1/3)


 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki


 /4 => 0<g(1)
/4 => 0<g(1)
