Dias
Επιφανές μέλος
Ο Dias αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Καθηγητής κι έχει σπουδάσει στο τμήμα Φυσικής ΕΚΠΑ (Αθήνα). Έχει γράψει 10.315 μηνύματα.

28-09-23

19:42
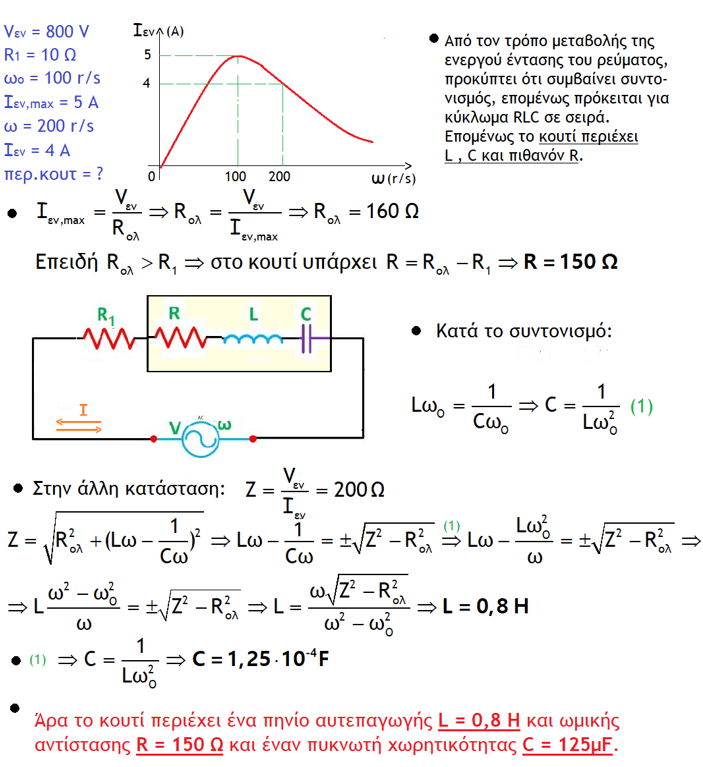
Τι λέτε για εναλλασσόμενο ρεύμα;

ΛΥΣΗ

eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.928 μηνύματα.

29-09-23

02:20
Oχι φιλε δεν ισχυει αυτο που λες.Αν θεωρεις οτι το μεγιστο στο διαστημα αυτο ειναι και μεγιστο εστω και τοπικο συνολικα ισχυει αλλα ειναι αυθαιρετο να το πας ετσι.Μεγιστο σε ενα ακρο υποδιαστηματος σε καμια περιπτωση δε θεωρειται τοπικο γτ ξαναλεω δεν πληρειται ο ορισμος!Αλλα εδω μιλαμε για το fermat.Δες το θεωρημα την διατυπωση.Σου λεει εστω η f ορισμενη σε ενα διαστημα Δ (ορισμενη σημαινει οτι το Δ ειναι υποδιαστημα του πεδιου ορισμου) και χ0 εσωτερικο του Δ.Ας πει και αλλος την αποψη του θεωρω παντως οτι δεν ισχυει ετσι.Δεν παίζει ρόλο το γεγονός οτι το α δεν είναι εσωτερικό σημείο του [0,α]. Εξακολουθεί να είναι εσωτερικό σημείο του πεδίου ορισμού οπότε το θεώρημα Fermat θα πρέπει να ισχύει κανονικά . Στην ουσία ισχυρίζομαι οτι το μέγιστο στο διάστημα αυτό θα είναι επιπλέον και το μέγιστο της f γενικά ( άρα θα είναι ακρότατο της f ).
Ο μονος τροπος που ειναι σωστο ειναι αν θεωρησεις απευθειας εστω οτι σε αυτο το α η f παρουσιαζει μεγιστο.
Τοτε ναι μπορεις να το ισχυριστεις.Απλα με τον τροπο που το διατυπωσες ειναι λαθος.
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 26 ετών, Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11.425 μηνύματα.

29-09-23

03:38
Το Fermat έχει κληθεί σωστά , γιατί υποθέτω εαν δεις οτι το α είναι ολικό μέγιστο της f . Έχω πράγματι λάθος όμως στην απόδειξη , και πρακτικό αλλά και διατύπωσης . Το πρώτο φαίνεται άμεσα απο το γεγονός οτι το συμπέρασμα του άτοπου μου σε εκείνο το σημείο δεν συνδέεται με την υπόθεση που οδήγησε στο άτοπο .Oχι φιλε δεν ισχυει αυτο που λες.Αν θεωρεις οτι το μεγιστο στο διαστημα αυτο ειναι και μεγιστο εστω και τοπικο συνολικα ισχυει αλλα ειναι αυθαιρετο να το πας ετσι.Μεγιστο σε ενα ακρο υποδιαστηματος σε καμια περιπτωση δε θεωρειται τοπικο γτ ξαναλεω δεν πληρειται ο ορισμος!Αλλα εδω μιλαμε για το fermat.Δες το θεωρημα την διατυπωση.Σου λεει εστω η f ορισμενη σε ενα διαστημα Δ (ορισμενη σημαινει οτι το Δ ειναι υποδιαστημα του πεδιου ορισμου) και χ0 εσωτερικο του Δ.Ας πει και αλλος την αποψη του θεωρω παντως οτι δεν ισχυει ετσι.
Σου παραθέτω μια τροποποιημένη απόδειξη να την ελέγξεις ( τελικά καλύτερα τα μαθηματικα να τα κάνει κανείς το πρωί ) :
Ας υποθέσουμε οτι το χ = α είναι η θέση μεγίστου της f . Σε αυτή την περίπτωση επειδή η f είναι παραγωγίσιμη , και παρουσιάζει ακρότατο στο α , το οποίο είναι εσωτερικό σημείο του πεδίου ορισμού , θα ισχύει απο το Θ.Fermat :
f'(α) = 0
Το α όμως είναι το μοναδικό σημείο καμπής . Οπότε αυτό σημαίνει οτι η f αλλάζει κυρτότητα εκατέρωθεν του α. Απο το ΘΜΤ για την f στο [0,α] θα υπάρχει ξ Ε (0,α) :
f'(ξ) = f(α)/α , το οποίο είναι θετικό καθώς α > 0 και f(x) > 0 για κάθε χ > 0.
Έτσι έχουμε ξ < α , με f'(ξ) > f'(α) = 0
Δηλαδή η f' είναι γνησίως φθίνουσα στο [0,α] και γνησίως αύξουσα για χ > α .
Απο το ΘΜΤ όμως για την f στο [α,χ] , υπάρχει ζ Ε (α,χ) :
f'(ζ) = [ f(χ) - f(α) ]/(χ - α)
Εφόσον ζ > α θα πρέπει να ισχύει το εξής εφόσον η f' είναι γνησίως αύξουσα για χ > α :
f'(ζ) > f'(α) = 0 =>
[ f(χ) - f(α) ]/(χ - α) > 0 =>
lim { [ f(χ) - f(α) ]/(χ - α) } > 0 =>
x->+oo
0 > 0
Άτοπο.
Επομένως το α δεν μπορεί να είναι μέγιστο της f . ( Αυτό είναι το σωστό συμπέρασμα του άτοπου ) .
--------------------------------------------------------------------------------------------------------------------------------------
Εδώ μπορεί να έχω κάποιο λάθος , είμαι λίγο νυσταγμένος
--------------------------------------------------------------------------------------------------------------------------------------
Επιπλέον δεν μπορεί να υπάρχει κάποιο μέγιστο για χ = χο > α , διότι τότε θα ήταν :
f(x) <= f(xo) κοντά στο xo .
Η f όμως είναι κυρτή για χ > α , άρα στο χο θα ισχύει :
f(x) >= f(xo) + f'(xo)(x - xo) = f(xo) => λόγω Θ.Fermat
f(x) >= f(xo)
Το οποίο είναι άτοπο .
--------------------------------------------------------------------------------------------------------------------------------------
Επομένως η θέση ενός πιθανού μέγιστου περιορίζεται στο διάστημα [0,α] . Το ΘΜΕΤ εξασφαλίζει οτι η f πράγματι θα έχει μια μέγιστη και μια ελάχιστη τιμή σε αυτό το διάστημα . Το 0 δεν μπορεί να είναι μέγιστο γιατί ξέρουμε οτι f(x) > 0 για κάθε x > 0 , και f(x) = 0 μόνο όταν χ = 0 . Οπότε 0 θα είναι θέση ελαχίστου . Εαν απο την άλλη το α ήταν το μέγιστο της f στο [0,α] , αυτό θα το έκανε και μέγιστο της f σε όλο το Df , το οποίο είναι άτοπο καθώς δείξαμε οτι το α δεν μπορεί να είναι μέγιστο της f . Οπότε αναγκαστικά η θέση μεγίστου b E (0,α) .
f'(α) = 0
Το α όμως είναι το μοναδικό σημείο καμπής . Οπότε αυτό σημαίνει οτι η f αλλάζει κυρτότητα εκατέρωθεν του α. Απο το ΘΜΤ για την f στο [0,α] θα υπάρχει ξ Ε (0,α) :
f'(ξ) = f(α)/α , το οποίο είναι θετικό καθώς α > 0 και f(x) > 0 για κάθε χ > 0.
Έτσι έχουμε ξ < α , με f'(ξ) > f'(α) = 0
Δηλαδή η f' είναι γνησίως φθίνουσα στο [0,α] και γνησίως αύξουσα για χ > α .
Απο το ΘΜΤ όμως για την f στο [α,χ] , υπάρχει ζ Ε (α,χ) :
f'(ζ) = [ f(χ) - f(α) ]/(χ - α)
Εφόσον ζ > α θα πρέπει να ισχύει το εξής εφόσον η f' είναι γνησίως αύξουσα για χ > α :
f'(ζ) > f'(α) = 0 =>
[ f(χ) - f(α) ]/(χ - α) > 0 =>
lim { [ f(χ) - f(α) ]/(χ - α) } > 0 =>
x->+oo
0 > 0
Άτοπο.
Επομένως το α δεν μπορεί να είναι μέγιστο της f . ( Αυτό είναι το σωστό συμπέρασμα του άτοπου ) .
--------------------------------------------------------------------------------------------------------------------------------------
Εδώ μπορεί να έχω κάποιο λάθος , είμαι λίγο νυσταγμένος
--------------------------------------------------------------------------------------------------------------------------------------
Επιπλέον δεν μπορεί να υπάρχει κάποιο μέγιστο για χ = χο > α , διότι τότε θα ήταν :
f(x) <= f(xo) κοντά στο xo .
Η f όμως είναι κυρτή για χ > α , άρα στο χο θα ισχύει :
f(x) >= f(xo) + f'(xo)(x - xo) = f(xo) => λόγω Θ.Fermat
f(x) >= f(xo)
Το οποίο είναι άτοπο .
--------------------------------------------------------------------------------------------------------------------------------------
Επομένως η θέση ενός πιθανού μέγιστου περιορίζεται στο διάστημα [0,α] . Το ΘΜΕΤ εξασφαλίζει οτι η f πράγματι θα έχει μια μέγιστη και μια ελάχιστη τιμή σε αυτό το διάστημα . Το 0 δεν μπορεί να είναι μέγιστο γιατί ξέρουμε οτι f(x) > 0 για κάθε x > 0 , και f(x) = 0 μόνο όταν χ = 0 . Οπότε 0 θα είναι θέση ελαχίστου . Εαν απο την άλλη το α ήταν το μέγιστο της f στο [0,α] , αυτό θα το έκανε και μέγιστο της f σε όλο το Df , το οποίο είναι άτοπο καθώς δείξαμε οτι το α δεν μπορεί να είναι μέγιστο της f . Οπότε αναγκαστικά η θέση μεγίστου b E (0,α) .
Dias
Επιφανές μέλος
Ο Dias αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Καθηγητής κι έχει σπουδάσει στο τμήμα Φυσικής ΕΚΠΑ (Αθήνα). Έχει γράψει 10.315 μηνύματα.

29-09-23

13:59
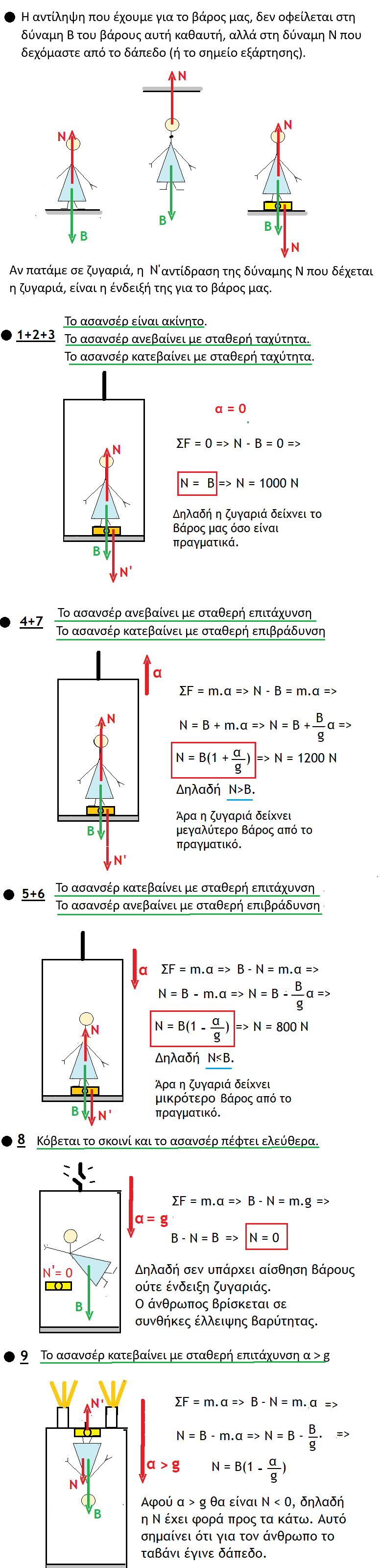
Στο ασανσέρ νοιώθετε άλλοτε βαρύτεροι και άλλοτε ελαφρύτεροι από το κανονικό. Να δούμε γιατί;

ΛΥΣΗ

eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.928 μηνύματα.

29-09-23

14:48
E αυτο που σου ειπα εκανες τελικα.Υπεθεσες οτι το α ειναι σημειου μεγιστου οποτε κανονικα ισχυει το fermat.Aπλα μπερδευτηκες με το θεωρημα μεγιστης και ελαιχτης τιμηςΤο Fermat έχει κληθεί σωστά , γιατί υποθέτω εαν δεις οτι το α είναι ολικό μέγιστο της f . Έχω πράγματι λάθος όμως στην απόδειξη , και πρακτικό αλλά και διατύπωσης . Το πρώτο φαίνεται άμεσα απο το γεγονός οτι το συμπέρασμα του άτοπου μου σε εκείνο το σημείο δεν συνδέεται με την υπόθεση που οδήγησε στο άτοπο .
Σου παραθέτω μια τροποποιημένη απόδειξη να την ελέγξεις ( τελικά καλύτερα τα μαθηματικα να τα κάνει κανείς το πρωί ) :
Ας υποθέσουμε οτι το χ = α είναι η θέση μεγίστου της f . Σε αυτή την περίπτωση επειδή η f είναι παραγωγίσιμη , και παρουσιάζει ακρότατο στο α , το οποίο είναι εσωτερικό σημείο του πεδίου ορισμού , θα ισχύει απο το Θ.Fermat :
f'(α) = 0
Το α όμως είναι το μοναδικό σημείο καμπής . Οπότε αυτό σημαίνει οτι η f αλλάζει κυρτότητα εκατέρωθεν του α. Απο το ΘΜΤ για την f στο [0,α] θα υπάρχει ξ Ε (0,α) :
f'(ξ) = f(α)/α , το οποίο είναι θετικό καθώς α > 0 και f(x) > 0 για κάθε χ > 0.
Έτσι έχουμε ξ < α , με f'(ξ) > f'(α) = 0
Δηλαδή η f' είναι γνησίως φθίνουσα στο [0,α] και γνησίως αύξουσα για χ > α .
Απο το ΘΜΤ όμως για την f στο [α,χ] , υπάρχει ζ Ε (α,χ) :
f'(ζ) = [ f(χ) - f(α) ]/(χ - α)
Εφόσον ζ > α θα πρέπει να ισχύει το εξής εφόσον η f' είναι γνησίως αύξουσα για χ > α :
f'(ζ) > f'(α) = 0 =>
[ f(χ) - f(α) ]/(χ - α) > 0 =>
lim { [ f(χ) - f(α) ]/(χ - α) } > 0 =>
x->+oo
0 > 0
Άτοπο.
Επομένως το α δεν μπορεί να είναι μέγιστο της f . ( Αυτό είναι το σωστό συμπέρασμα του άτοπου ) .
--------------------------------------------------------------------------------------------------------------------------------------
Εδώ μπορεί να έχω κάποιο λάθος , είμαι λίγο νυσταγμένος
--------------------------------------------------------------------------------------------------------------------------------------
Επιπλέον δεν μπορεί να υπάρχει κάποιο μέγιστο για χ = χο > α , διότι τότε θα ήταν :
f(x) <= f(xo) κοντά στο xo .
Η f όμως είναι κυρτή για χ > α , άρα στο χο θα ισχύει :
f(x) >= f(xo) + f'(xo)(x - xo) = f(xo) => λόγω Θ.Fermat
f(x) >= f(xo)
Το οποίο είναι άτοπο .
--------------------------------------------------------------------------------------------------------------------------------------
Επομένως η θέση ενός πιθανού μέγιστου περιορίζεται στο διάστημα [0,α] . Το ΘΜΕΤ εξασφαλίζει οτι η f πράγματι θα έχει μια μέγιστη και μια ελάχιστη τιμή σε αυτό το διάστημα . Το 0 δεν μπορεί να είναι μέγιστο γιατί ξέρουμε οτι f(x) > 0 για κάθε x > 0 , και f(x) = 0 μόνο όταν χ = 0 . Οπότε 0 θα είναι θέση ελαχίστου . Εαν απο την άλλη το α ήταν το μέγιστο της f στο [0,α] , αυτό θα το έκανε και μέγιστο της f σε όλο το Df , το οποίο είναι άτοπο καθώς δείξαμε οτι το α δεν μπορεί να είναι μέγιστο της f . Οπότε αναγκαστικά η θέση μεγίστου b E (0,α) .
Αυτόματη ένωση συνεχόμενων μηνυμάτων:
Ωχ παλι υπαρχει λαθος.Λες f(x)-f(a)/x-a>0 μετα λες αφου υπαρχει το οριο limf(x)-f(a)/x-a>0 ομως η ιδιοτητα λεει οτι αν εχεις f(x)>g(x) και υπαρχουν τα ορια ειναι limf(x)>=limg(x).Eνω αν εχεις limf(x)>0 πραγματι κοντα στο χ0 ειναι f(x) καθαρα θετικο.Το Fermat έχει κληθεί σωστά , γιατί υποθέτω εαν δεις οτι το α είναι ολικό μέγιστο της f . Έχω πράγματι λάθος όμως στην απόδειξη , και πρακτικό αλλά και διατύπωσης . Το πρώτο φαίνεται άμεσα απο το γεγονός οτι το συμπέρασμα του άτοπου μου σε εκείνο το σημείο δεν συνδέεται με την υπόθεση που οδήγησε στο άτοπο .
Σου παραθέτω μια τροποποιημένη απόδειξη να την ελέγξεις ( τελικά καλύτερα τα μαθηματικα να τα κάνει κανείς το πρωί ) :
Ας υποθέσουμε οτι το χ = α είναι η θέση μεγίστου της f . Σε αυτή την περίπτωση επειδή η f είναι παραγωγίσιμη , και παρουσιάζει ακρότατο στο α , το οποίο είναι εσωτερικό σημείο του πεδίου ορισμού , θα ισχύει απο το Θ.Fermat :
f'(α) = 0
Το α όμως είναι το μοναδικό σημείο καμπής . Οπότε αυτό σημαίνει οτι η f αλλάζει κυρτότητα εκατέρωθεν του α. Απο το ΘΜΤ για την f στο [0,α] θα υπάρχει ξ Ε (0,α) :
f'(ξ) = f(α)/α , το οποίο είναι θετικό καθώς α > 0 και f(x) > 0 για κάθε χ > 0.
Έτσι έχουμε ξ < α , με f'(ξ) > f'(α) = 0
Δηλαδή η f' είναι γνησίως φθίνουσα στο [0,α] και γνησίως αύξουσα για χ > α .
Απο το ΘΜΤ όμως για την f στο [α,χ] , υπάρχει ζ Ε (α,χ) :
f'(ζ) = [ f(χ) - f(α) ]/(χ - α)
Εφόσον ζ > α θα πρέπει να ισχύει το εξής εφόσον η f' είναι γνησίως αύξουσα για χ > α :
f'(ζ) > f'(α) = 0 =>
[ f(χ) - f(α) ]/(χ - α) > 0 =>
lim { [ f(χ) - f(α) ]/(χ - α) } > 0 =>
x->+oo
0 > 0
Άτοπο.
Επομένως το α δεν μπορεί να είναι μέγιστο της f . ( Αυτό είναι το σωστό συμπέρασμα του άτοπου ) .
--------------------------------------------------------------------------------------------------------------------------------------
Εδώ μπορεί να έχω κάποιο λάθος , είμαι λίγο νυσταγμένος
--------------------------------------------------------------------------------------------------------------------------------------
Επιπλέον δεν μπορεί να υπάρχει κάποιο μέγιστο για χ = χο > α , διότι τότε θα ήταν :
f(x) <= f(xo) κοντά στο xo .
Η f όμως είναι κυρτή για χ > α , άρα στο χο θα ισχύει :
f(x) >= f(xo) + f'(xo)(x - xo) = f(xo) => λόγω Θ.Fermat
f(x) >= f(xo)
Το οποίο είναι άτοπο .
--------------------------------------------------------------------------------------------------------------------------------------
Επομένως η θέση ενός πιθανού μέγιστου περιορίζεται στο διάστημα [0,α] . Το ΘΜΕΤ εξασφαλίζει οτι η f πράγματι θα έχει μια μέγιστη και μια ελάχιστη τιμή σε αυτό το διάστημα . Το 0 δεν μπορεί να είναι μέγιστο γιατί ξέρουμε οτι f(x) > 0 για κάθε x > 0 , και f(x) = 0 μόνο όταν χ = 0 . Οπότε 0 θα είναι θέση ελαχίστου . Εαν απο την άλλη το α ήταν το μέγιστο της f στο [0,α] , αυτό θα το έκανε και μέγιστο της f σε όλο το Df , το οποίο είναι άτοπο καθώς δείξαμε οτι το α δεν μπορεί να είναι μέγιστο της f . Οπότε αναγκαστικά η θέση μεγίστου b E (0,α) .
Αυτόματη ένωση συνεχόμενων μηνυμάτων:
Λοιπον απο οτι καταλαβα σωστα εχεις απορριψει το μεγιστο για τα χ>α.Το θεμα ειναι οτι εντελει δεν εβγαλες σωστα το ατοπο για το α.Επισης,το γεγονος οτι ειναι μεγιστο στο διαστημα [0,α] σε καμια περιπτωση δεν σου διασφαλιζει οτι ειναι ολικο μεγιστο οπως θες ακομα και το εσωτερικο του [0,α] να παρεις.Απλα σιγουρα αν απορριψεις το α αφοβα εχεις βγαλει το f'(εσωτερικου σημειου)=0 επομενως εκει θα πρεπει να βγαλεις συνολικα απο αριστερα και δεξια οτι ειναι αρνητικα και θετικο οποτε οκ.Μηπως η εκφωνηση λεει τοπικο μεγιστο και οχι ολικο μεγιστο??Το Fermat έχει κληθεί σωστά , γιατί υποθέτω εαν δεις οτι το α είναι ολικό μέγιστο της f . Έχω πράγματι λάθος όμως στην απόδειξη , και πρακτικό αλλά και διατύπωσης . Το πρώτο φαίνεται άμεσα απο το γεγονός οτι το συμπέρασμα του άτοπου μου σε εκείνο το σημείο δεν συνδέεται με την υπόθεση που οδήγησε στο άτοπο .
Σου παραθέτω μια τροποποιημένη απόδειξη να την ελέγξεις ( τελικά καλύτερα τα μαθηματικα να τα κάνει κανείς το πρωί ) :
Ας υποθέσουμε οτι το χ = α είναι η θέση μεγίστου της f . Σε αυτή την περίπτωση επειδή η f είναι παραγωγίσιμη , και παρουσιάζει ακρότατο στο α , το οποίο είναι εσωτερικό σημείο του πεδίου ορισμού , θα ισχύει απο το Θ.Fermat :
f'(α) = 0
Το α όμως είναι το μοναδικό σημείο καμπής . Οπότε αυτό σημαίνει οτι η f αλλάζει κυρτότητα εκατέρωθεν του α. Απο το ΘΜΤ για την f στο [0,α] θα υπάρχει ξ Ε (0,α) :
f'(ξ) = f(α)/α , το οποίο είναι θετικό καθώς α > 0 και f(x) > 0 για κάθε χ > 0.
Έτσι έχουμε ξ < α , με f'(ξ) > f'(α) = 0
Δηλαδή η f' είναι γνησίως φθίνουσα στο [0,α] και γνησίως αύξουσα για χ > α .
Απο το ΘΜΤ όμως για την f στο [α,χ] , υπάρχει ζ Ε (α,χ) :
f'(ζ) = [ f(χ) - f(α) ]/(χ - α)
Εφόσον ζ > α θα πρέπει να ισχύει το εξής εφόσον η f' είναι γνησίως αύξουσα για χ > α :
f'(ζ) > f'(α) = 0 =>
[ f(χ) - f(α) ]/(χ - α) > 0 =>
lim { [ f(χ) - f(α) ]/(χ - α) } > 0 =>
x->+oo
0 > 0
Άτοπο.
Επομένως το α δεν μπορεί να είναι μέγιστο της f . ( Αυτό είναι το σωστό συμπέρασμα του άτοπου ) .
--------------------------------------------------------------------------------------------------------------------------------------
Εδώ μπορεί να έχω κάποιο λάθος , είμαι λίγο νυσταγμένος
--------------------------------------------------------------------------------------------------------------------------------------
Επιπλέον δεν μπορεί να υπάρχει κάποιο μέγιστο για χ = χο > α , διότι τότε θα ήταν :
f(x) <= f(xo) κοντά στο xo .
Η f όμως είναι κυρτή για χ > α , άρα στο χο θα ισχύει :
f(x) >= f(xo) + f'(xo)(x - xo) = f(xo) => λόγω Θ.Fermat
f(x) >= f(xo)
Το οποίο είναι άτοπο .
--------------------------------------------------------------------------------------------------------------------------------------
Επομένως η θέση ενός πιθανού μέγιστου περιορίζεται στο διάστημα [0,α] . Το ΘΜΕΤ εξασφαλίζει οτι η f πράγματι θα έχει μια μέγιστη και μια ελάχιστη τιμή σε αυτό το διάστημα . Το 0 δεν μπορεί να είναι μέγιστο γιατί ξέρουμε οτι f(x) > 0 για κάθε x > 0 , και f(x) = 0 μόνο όταν χ = 0 . Οπότε 0 θα είναι θέση ελαχίστου . Εαν απο την άλλη το α ήταν το μέγιστο της f στο [0,α] , αυτό θα το έκανε και μέγιστο της f σε όλο το Df , το οποίο είναι άτοπο καθώς δείξαμε οτι το α δεν μπορεί να είναι μέγιστο της f . Οπότε αναγκαστικά η θέση μεγίστου b E (0,α) .
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 26 ετών, Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11.425 μηνύματα.

29-09-23

15:26
Θα κάτσω να το δω αναλυτικά κάποια στιγμή πρωί τις επόμενες μέρες γιατί όλο τα κοιτάω το βράδυ και ξεκάθαρα δεν έχει νόημα γιατί γίνονται συνεχώς λάθη .E αυτο που σου ειπα εκανες τελικα.Υπεθεσες οτι το α ειναι σημειου μεγιστου οποτε κανονικα ισχυει το fermat.Aπλα μπερδευτηκες με το θεωρημα μεγιστης και ελαιχτης τιμης
Αυτόματη ένωση συνεχόμενων μηνυμάτων:
Ωχ παλι υπαρχει λαθος.Λες f(x)-f(a)/x-a>0 μετα λες αφου υπαρχει το οριο limf(x)-f(a)/x-a>0 ομως η ιδιοτητα λεει οτι αν εχεις f(x)>g(x) και υπαρχουν τα ορια ειναι limf(x)>=limg(x).Eνω αν εχεις limf(x)>0 πραγματι κοντα στο χ0 ειναι f(x) καθαρα θετικο.
Αυτόματη ένωση συνεχόμενων μηνυμάτων:
Λοιπον απο οτι καταλαβα σωστα εχεις απορριψει το μεγιστο για τα χ>α.Το θεμα ειναι οτι εντελει δεν εβγαλες σωστα το ατοπο για το α.Επισης,το γεγονος οτι ειναι μεγιστο στο διαστημα [0,α] σε καμια περιπτωση δεν σου διασφαλιζει οτι ειναι ολικο μεγιστο οπως θες ακομα και το εσωτερικο του [0,α] να παρεις.Απλα σιγουρα αν απορριψεις το α αφοβα εχεις βγαλει το f'(εσωτερικου σημειου)=0 επομενως εκει θα πρεπει να βγαλεις συνολικα απο αριστερα και δεξια οτι ειναι αρνητικα και θετικο οποτε οκ.Μηπως η εκφωνηση λεει τοπικο μεγιστο και οχι ολικο μεγιστο??
Τώρα σχετικά με αυτό που λες στο τέλος...δεν ξέρω , επειδή γράφει ο Cade , την μέγιστη τιμή της , εγώ αντιλαμβάνομαι το ολικό μέγιστο . Διαφορετικά δεν θα έλεγε δείξτε οτι η f έχει μέγιστο στο στο (0,α) ;
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.928 μηνύματα.

29-09-23

15:32
Ναι και γω πιστευω οτι ολικο μεγιστο εννοει.Απλα αν εννοουσε τοπικο μεγιστο απαξ και τελειωνες με το α οτι δεν ειναι τοπικο μεγιστο τελειωνε η ιστορια.Θα κάτσω να το δω αναλυτικά κάποια στιγμή πρωί τις επόμενες μέρες γιατί όλο τα κοιτάω το βράδυ και ξεκάθαρα δεν έχει νόημα γιατί γίνονται συνεχώς λάθη .
Τώρα σχετικά με αυτό που λες στο τέλος...δεν ξέρω , επειδή γράφει ο Cade , την μέγιστη τιμή της , εγώ αντιλαμβάνομαι το ολικό μέγιστο . Διαφορετικά δεν θα έλεγε δείξτε οτι η f έχει μέγιστο στο στο (0,α) ;
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 26 ετών, Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11.425 μηνύματα.

29-09-23

15:52
Τούτο πως σου φαίνεται ;Ναι και γω πιστευω οτι ολικο μεγιστο εννοει.Απλα αν εννοουσε τοπικο μεγιστο απαξ και τελειωνες με το α οτι δεν ειναι τοπικο μεγιστο τελειωνε η ιστορια.
Δείξαμε οτι f' είναι γνησίως αύξουσα για χ >= α .
Για κάθε x > α λοιπόν :
f'(x) > f'(α) = 0
Δηλαδή και η f είναι γνησίως αύξουσα για χ > α .
Άρα f(x) > f(α) , για κάθε x > α .
Παίρνοντας το όριο καθώς το χ τείνει στο +οο :
lim f(x) >= f(α) =>
x-> +oo
f(α) <= 0
Άτοπο .
Άρα το α δεν μπορεί να είναι μέγιστο .
Κοίτα , αυτό που λες τώρα σχετικά με το local vs global μέγιστο πρέπει να το σκεφτώ λίγο παραπάνω . Πιστεύω θέμα διατύπωσης θα είναι και εδώ πιο πολύ .
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.928 μηνύματα.

29-09-23

18:48
Ωραιος!Απο την ωρα που εφτασες f(x)>f(a) δεν χρειαζοταν να συνεχισεις!Ηταν δεδομενο οτι δεν μπορει να εχει μεγιστο στο α.Επομενως τωρα ειμαστε σιγουροι οτι στο ξ που ανηκει στο (0,α) εχει τοπικο μεγιστο αρα πρεπει να βγαλουμε το ολικο μεγιστοΤούτο πως σου φαίνεται ;
Δείξαμε οτι f' είναι γνησίως αύξουσα για χ >= α .
Για κάθε x > α λοιπόν :
f'(x) > f'(α) = 0
Δηλαδή και η f είναι γνησίως αύξουσα για χ > α .
Άρα f(x) > f(α) , για κάθε x > α .
Παίρνοντας το όριο καθώς το χ τείνει στο +οο :
lim f(x) >= f(α) =>
x-> +oo
f(α) <= 0
Άτοπο .
Άρα το α δεν μπορεί να είναι μέγιστο .
Κοίτα , αυτό που λες τώρα σχετικά με το local vs global μέγιστο πρέπει να το σκεφτώ λίγο παραπάνω . Πιστεύω θέμα διατύπωσης θα είναι και εδώ πιο πολύ
Cade
Πολύ δραστήριο μέλος
Ο Cade αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Απόφοιτος λυκείου. Έχει γράψει 856 μηνύματα.

29-09-23

23:37
Η άσκηση αναφέρεται σε ολικό μέγιστο.Μηπως η εκφωνηση λεει τοπικο μεγιστο και οχι ολικο μεγιστο?
Μια συνάρτηση που βρήκα και φαίνεται να ικανοποιεί τα δεδομένα είναι η f(x)=xe^(-x).
Μάλιστα για κ=1/e => b=1 και f(1)=1/e το οποίο όντως είναι το ολικό μέγιστο της συνάρτησης που ανέφερα παραπάνω.Ορίζω g(x)=f(-lnx), 0<x≤1, g(0)=0. Η g είναι συνεχής και επειδή g(0)=0=g(1), g>0 παίρνει μέγιστη τιμή σε κάποιο κε(0,1). Οπότε η f παίρνει μέγιστη τιμή στο b=-lnκ.
άσκηση #5
Έστω οι συνεχείς συναρτήσεις f,g: [0,1]->R με g γνησίως αύξουσα. Αν ισχύει:
να δειχθεί ότι η εξίσωση f(x)=0 έχει 2 τουλάχιστον ρίζες στο (0,1).
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.928 μηνύματα.

30-09-23

12:42
ok μια λυση που να ναι καθολικη θελουμε ομως οχι μια συναρτηση που ικανοποιει αυτες τις προυποθεσεις.Η άσκηση αναφέρεται σε ολικό μέγιστο.
Μια συνάρτηση που βρήκα και φαίνεται να ικανοποιεί τα δεδομένα είναι η f(x)=xe^(-x).
----------------Μάλιστα για κ=1/e => b=1 και f(1)=1/e το οποίο όντως είναι το ολικό μέγιστο της συνάρτησης που ανέφερα παραπάνω.
View attachment 122906
άσκηση #5
Έστω οι συνεχείς συναρτήσεις f,g: [0,1]->R με g γνησίως αύξουσα. Αν ισχύει:
View attachment 122926
να δειχθεί ότι η εξίσωση f(x)=0 έχει 2 τουλάχιστον ρίζες στο (0,1).
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.928 μηνύματα.

30-09-23

14:05
Η μια ριζα βγαινει με rolle για την συναρτηση ολοκληρωμα απο 0 εως χ f(t)dt στο [0,1].Tωρα για την αλλη ισως παει με ατοπο.Δεν ξερω
Dias
Επιφανές μέλος
Ο Dias αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Καθηγητής κι έχει σπουδάσει στο τμήμα Φυσικής ΕΚΠΑ (Αθήνα). Έχει γράψει 10.315 μηνύματα.

30-09-23

16:15
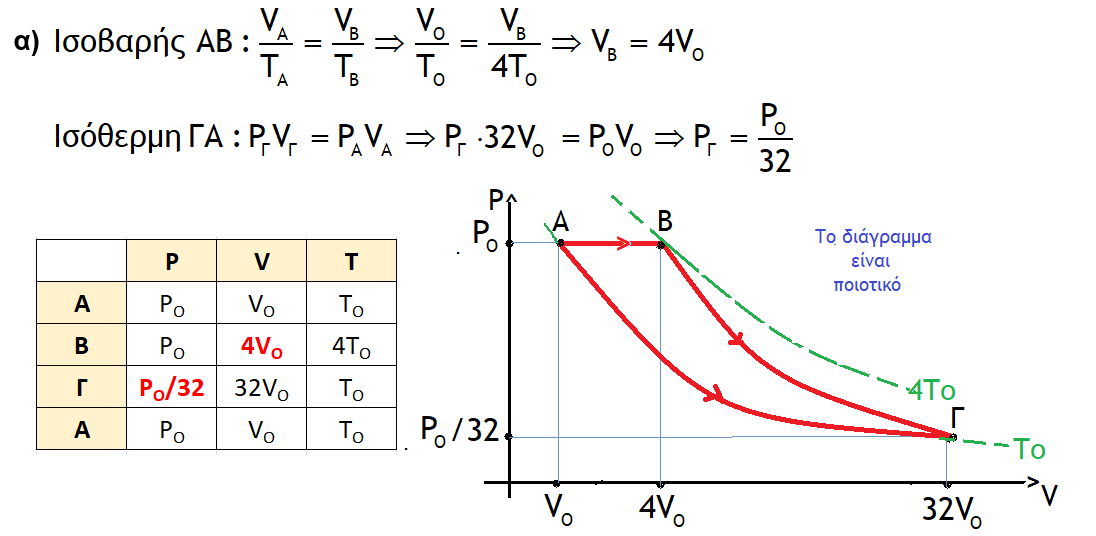
Τι θα λέγατε για λίγη (απλή) Θερμοδυναμική;

ΛΥΣΗ

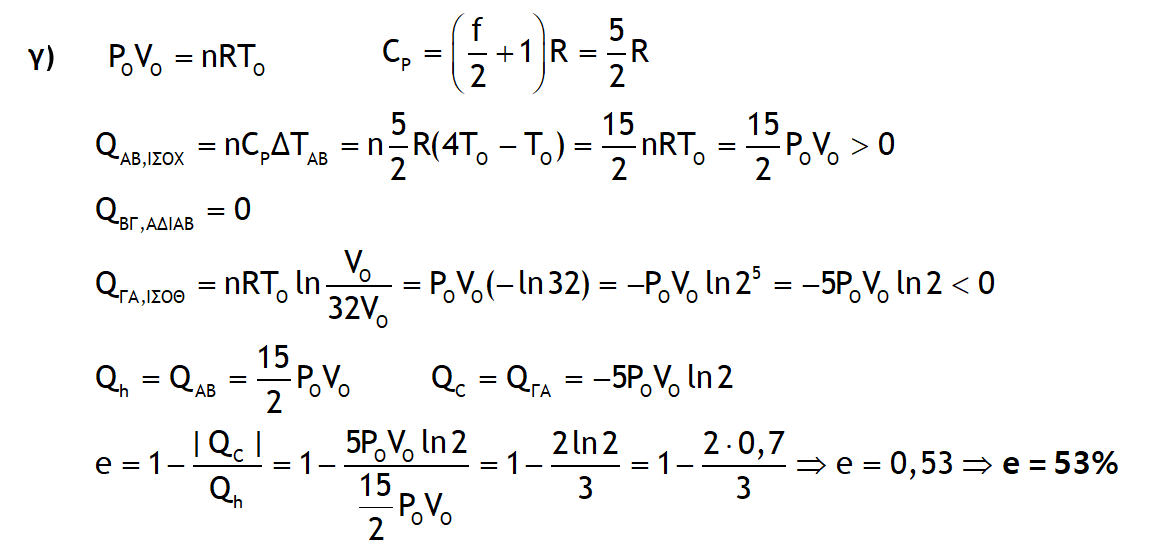
Cade
Πολύ δραστήριο μέλος
Ο Cade αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Απόφοιτος λυκείου. Έχει γράψει 856 μηνύματα.

30-09-23

19:02
Αφού δεν έχουμε κάπου αλλού μεγιστο αρκεί να δείξουμε ότι η f είναι κοίλη στο (0,α) και τελειώσαμεΕπομενως τωρα ειμαστε σιγουροι οτι στο ξ που ανηκει στο (0,α) εχει τοπικο μεγιστο αρα πρεπει να βγαλουμε το ολικο μεγιστο
γιαννης_00
Επιφανές μέλος
Ο γιαννης_00 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 24 ετών, Φοιτητής του τμήματος Πρόγραμμα Ιερατικών Σπουδών και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 12.981 μηνύματα.

30-09-23

19:39
Στη φυσικη ονομαζουμε ελευθερη πτωση σωματος οταν αυτο θα κινηθει με μονη δρωσα δυναμη επ αυτου το βαρος...
Αφαιρουμε και τον αερα και καταληγουμε στις παρακατω γνωστες σχεσεις..
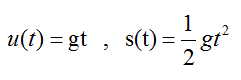
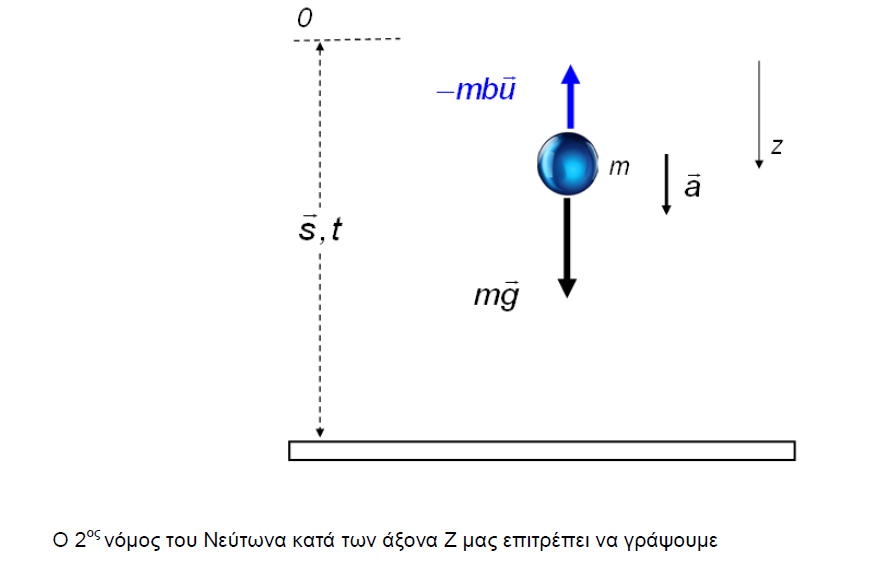
Τι θα γινοταν αν βαζαμε και τον αερα στο σεναριο μας ...πως θα ηταν αυτες οι σχεσεις?
Ασκηση απο Θ .Αλεξοπουλο ..σεμφε




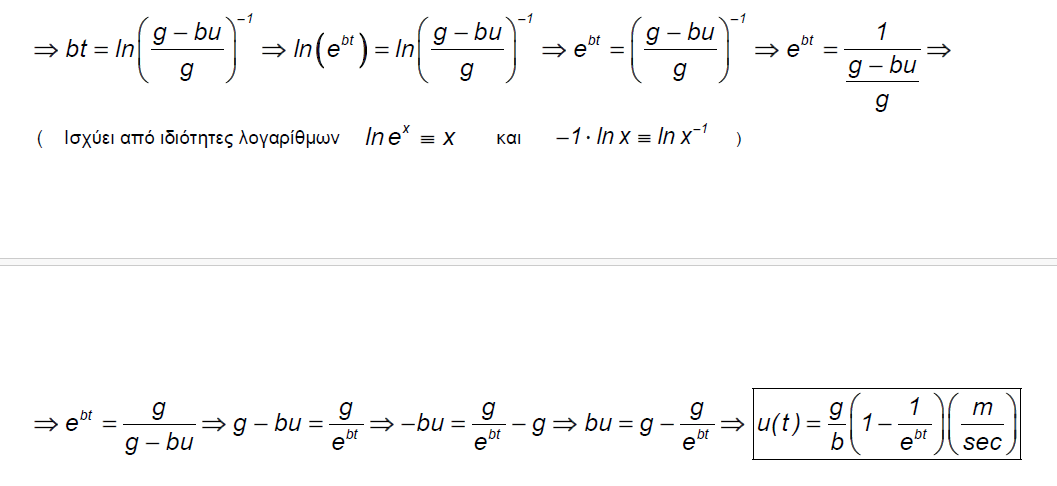


Καλα εντελως τζαζ σχεσεις ...Η φυση θελει το e της και το ln της.
Αφαιρουμε και τον αερα και καταληγουμε στις παρακατω γνωστες σχεσεις..
Τι θα γινοταν αν βαζαμε και τον αερα στο σεναριο μας ...πως θα ηταν αυτες οι σχεσεις?
Ασκηση απο Θ .Αλεξοπουλο ..σεμφε
Καλα εντελως τζαζ σχεσεις ...Η φυση θελει το e της και το ln της.
Dias
Επιφανές μέλος
Ο Dias αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Καθηγητής κι έχει σπουδάσει στο τμήμα Φυσικής ΕΚΠΑ (Αθήνα). Έχει γράψει 10.315 μηνύματα.

30-09-23

23:46
γιαννης_00
1) Γιάννη μου, μπράβο σου για τη δουλειά και την παρουσίαση που έκανες!
2) Θέλω να συμπληρώσω τη μελέτη σου από την ποιοτική όμως πλευρά.
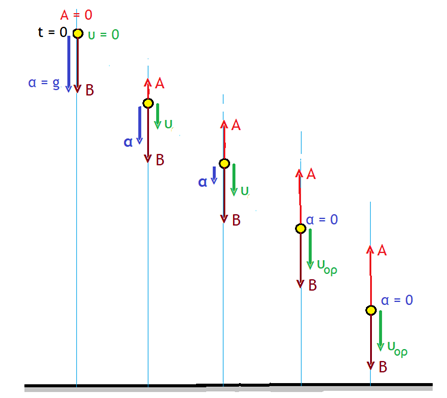 Όταν αφήνουμε ένα σώμα να πέσει από μεγάλο ύψος (όχι όμως τόσο μεγάλο ώστε να μεταβάλλεται αισθητά το g), σίγουρα υπάρχει και η αντίσταση του αέρα. Το σώμα αρχίζει επιταχυνόμενη κίνηση. Όμως η αντίσταση του αέρα αυξάνεται με την ταχύτητα, άρα η επιτάχυνση α = (Β – Α)/m διαρκώς μικραίνει. Αυτό σημαίνει ότι η κίνηση του σώματος είναι επιταχυνόμενη μεν, αλλά με διαρκώς μειούμενη επιτάχυνση. Έτσι η ταχύτητα αυξάνεται και η αντίσταση του αέρα καθώς αυξάνεται, κάποια στιγμή θα γίνει ίσου μέτρου με το βάρος, οπότε ΣF = 0. Επομένως από τη στιγμή αυτή και μετά η κίνηση θα είναι ομαλή με μέγιστη σταθερή οριακή (τερματική) ταχύτητα.
Όταν αφήνουμε ένα σώμα να πέσει από μεγάλο ύψος (όχι όμως τόσο μεγάλο ώστε να μεταβάλλεται αισθητά το g), σίγουρα υπάρχει και η αντίσταση του αέρα. Το σώμα αρχίζει επιταχυνόμενη κίνηση. Όμως η αντίσταση του αέρα αυξάνεται με την ταχύτητα, άρα η επιτάχυνση α = (Β – Α)/m διαρκώς μικραίνει. Αυτό σημαίνει ότι η κίνηση του σώματος είναι επιταχυνόμενη μεν, αλλά με διαρκώς μειούμενη επιτάχυνση. Έτσι η ταχύτητα αυξάνεται και η αντίσταση του αέρα καθώς αυξάνεται, κάποια στιγμή θα γίνει ίσου μέτρου με το βάρος, οπότε ΣF = 0. Επομένως από τη στιγμή αυτή και μετά η κίνηση θα είναι ομαλή με μέγιστη σταθερή οριακή (τερματική) ταχύτητα.
3) Η οριακή ταχύτητα έχει πολλές εφαρμογές. Οι αλεξιπτωτιστές δεν τσακίζονται, οι σταγόνες της βροχής δεν μας τραυματίζουν, οι σχετικές ασκήσεις στην επαγωγή είναι SOS.
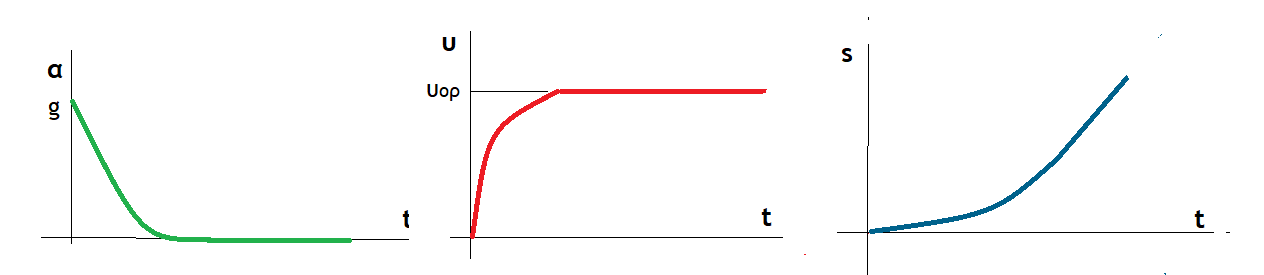
4) Οι ποιοτικές γραφικές παραστάσεις της κίνησης είναι:
 5) Ήθελα όμως να δω αν η θεωρία σου συμφωνεί με την ποιοτική μελέτη μου. Έτσι έβαλα τις εξισώσεις σου στο geobra (με αυθαίρετο b = 5) και να τι βγήκε:
5) Ήθελα όμως να δω αν η θεωρία σου συμφωνεί με την ποιοτική μελέτη μου. Έτσι έβαλα τις εξισώσεις σου στο geobra (με αυθαίρετο b = 5) και να τι βγήκε:
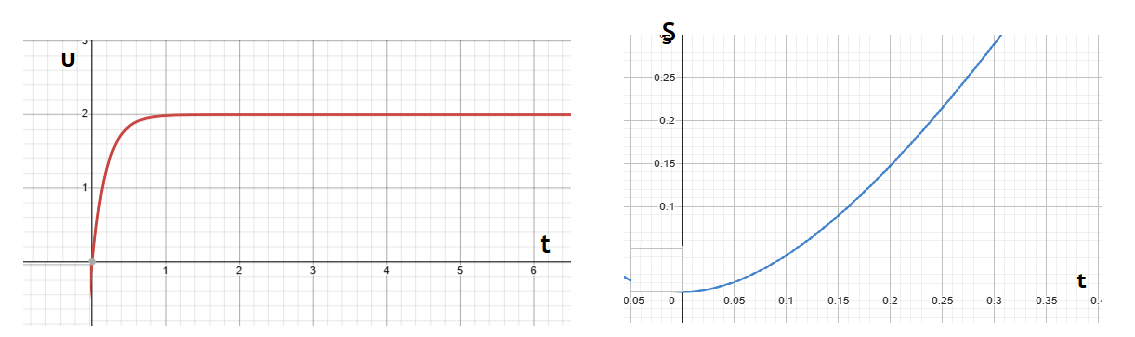
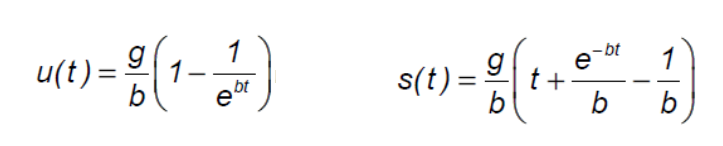 Καλό ε;6)
Καλό ε;6)

Σε πολλά στη φύση εμφανίζεται το e και ο lnx. Mα γιαυτό μας βρήκανε και δεν τα βρήκαμε.
7) Και πάλι μπράβο!!

1) Γιάννη μου, μπράβο σου για τη δουλειά και την παρουσίαση που έκανες!
2) Θέλω να συμπληρώσω τη μελέτη σου από την ποιοτική όμως πλευρά.
3) Η οριακή ταχύτητα έχει πολλές εφαρμογές. Οι αλεξιπτωτιστές δεν τσακίζονται, οι σταγόνες της βροχής δεν μας τραυματίζουν, οι σχετικές ασκήσεις στην επαγωγή είναι SOS.
4) Οι ποιοτικές γραφικές παραστάσεις της κίνησης είναι:
Σε πολλά στη φύση εμφανίζεται το e και ο lnx. Mα γιαυτό μας βρήκανε και δεν τα βρήκαμε.
7) Και πάλι μπράβο!!
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 26 ετών, Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11.425 μηνύματα.

01-10-23

00:12
@γιαννης_00 , πολύ καλή επιλογή προβλήματος . Ο αέρας αγνοείται πάντα στα περισσότερα προβλήματα αφήνοντας μια αισθηση πως οι νόμοι της φυσικής δεν είναι αρκετά πλήρεις( δεν είναι όντως αλλά σε τέτοιο επίπεδο είναι) ή οτι δεν περιγράφουν με αρκετή ακρίβεια τα καθημερινά φαινόμενα .γιαννης_00
1) Γιάννη μου, μπράβο σου για τη δουλειά και την παρουσίαση που έκανες!
2) Θέλω να συμπληρώσω τη μελέτη σου από την ποιοτική όμως πλευρά.
Όταν αφήνουμε ένα σώμα να πέσει από μεγάλο ύψος (όχι όμως τόσο μεγάλο ώστε να μεταβάλλεται αισθητά το g), σίγουρα υπάρχει και η αντίσταση του αέρα. Το σώμα αρχίζει επιταχυνόμενη κίνηση. Όμως η αντίσταση του αέρα αυξάνεται με την ταχύτητα, άρα η επιτάχυνση α = (Β – Α)/m διαρκώς μικραίνει. Αυτό σημαίνει ότι η κίνηση του σώματος είναι επιταχυνόμενη μεν, αλλά με διαρκώς μειούμενη επιτάχυνση. Έτσι η ταχύτητα αυξάνεται και η αντίσταση του αέρα καθώς αυξάνεται, κάποια στιγμή θα γίνει ίσου μέτρου με το βάρος, οπότε ΣF = 0. Επομένως από τη στιγμή αυτή και μετά η κίνηση θα είναι ομαλή με μέγιστη σταθερή οριακή (τερματική) ταχύτητα.
3) Η οριακή ταχύτητα έχει πολλές εφαρμογές. Οι αλεξιπτωτιστές δεν τσακίζονται, οι σταγόνες της βροχής δεν μας τραυματίζουν, οι σχετικές ασκήσεις στην επαγωγή είναι SOS.
4) Οι ποιοτικές γραφικές παραστάσεις της κίνησης είναι:
5) Ήθελα όμως να δω αν η θεωρία σου συμφωνεί με την ποιοτική μελέτη μου. Έτσι έβαλα τις εξισώσεις σου στο geobra (με αυθαίρετο b = 5) και να τι βγήκε:
6)
View attachment 123012
Σε πολλά στη φύση εμφανίζεται το e και ο lnx. Mα γιαυτό μας βρήκανε και δεν τα βρήκαμε.
7) Και πάλι μπράβο!!
@Dias πάρα πολύ όμορφη η ποιοτική περιγραφή σου Δία . Δυστυχώς ακόμα και στο πανεπιστήμιο όταν διδάσκεται τέτοια προβλήματα κανείς η έμφαση πέφτει εξολοκλήρου στην απάντηση και κανένας δεν κάθεται να σκεφτεί 5 λεπτά τι βρήκε και γιατί . Οπότε αναδεικνύεις κάτι πολύ σημαντικό , οτι ακόμα και ένας μαθητής χωρίς τις κατάλληλες μαθηματικές γνώσεις , εαν έχει καλή φυσική διαίσθηση μπορεί να κατανοήσει τι θα συμβεί !
Συμπληρώνω στα ενδεικτικά παραδείγματα σου και την κλασσική αντιμετώπιση των ηλεκτρονίων κατά την κίνηση τους μέσα στον κρύσταλλο ενός ημιαγωγού , ως μπίλιες που κινούνται με μια ισοδύναμη σταθερή ταχύτητα ( την γνωστή ταχύτητα ολίσθησης ) .
Στην πραγματικότητα τα ηλεκτρόνια συγκρούονται κατά μέσο ανά τ δευτερόλεπτα(στατιστικό μέγεθος φυσικά) . Στο διάστημα αυτό επιταχύνονται μέχρι να σκεδαστούν και μετά να αρχίσουν να επιταχύνονται πάλι μέχρι την επόμενη σκέδαση . Οπότε όλο αυτό μπορεί να περιγραφτεί ισοδύναμα με μια σταθερή ταχύτητα κίνησης , μικρότερη φυσικά απο την μέγιστη που αποκτούν στην πραγματικότητα .
Αυτή η ισοδύναμη σταθερή ταχύτητα εξαρτάται απο το εφαρμοζόμενο ηλεκτρικό πεδίο και την ευκινησία των ηλεκτρονίων μέσα στον κρύσταλλο . Για ίδια εφαρμοζόμενη τάση , στον κρύσταλλο με την μεγαλύτερη ευκινησία τα ηλεκτρόνια θα αποκτήσουν μεγαλύτερες ισοδύναμες ταχύτητες .
Το ενδιαφέρον είναι οτι μετά απο μια τιμή του εφαρμοζόμενου ηλεκτρικού πεδίου η ισοδύναμη αυτή σταθερή ταχύτητα δεν μπορεί να αυξηθεί άλλο καθώς η ευκινησία αρχίζει να μειώνεται ( οι κρούσιες γίνονται πολύ συχνές για να προλάβει να επιταχυνθεί αρκετά το ηλεκτρόνιο ) . Για παράδειγμα σε έναν ημιαγωγό < 1 μm σε μήκος , οι τάσεις που απαιτούνται για να δημιουργηθούν μεγάλα ηλεκτρικά πεδία που θα προκαλέσουν τον κορεσμό στην ταχύτητα των ηλεκτρονίων , είναι της τάξεως των δεκάδων mV . Πολύ μικρότερες απο αυτές που εφαρμόζονται συνήθως στις πραγματικές διατάξεις .
γιαννης_00
Επιφανές μέλος
Ο γιαννης_00 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 24 ετών, Φοιτητής του τμήματος Πρόγραμμα Ιερατικών Σπουδών και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 12.981 μηνύματα.

01-10-23

01:59
Ευχαριστω παιδια ..ναι ετσι σωστα ,ειναι η οριακη ταχυτητα..
Eχω και μια ασκησουλα με οριακη ταχυτητα αλλα μεσα σε νερακι (αρχη μετρηση ιξωδους) με εκεινο τον νομο του stokes..αλλη φορα
Eχω και μια ασκησουλα με οριακη ταχυτητα αλλα μεσα σε νερακι (αρχη μετρηση ιξωδους) με εκεινο τον νομο του stokes..αλλη φορα
γιαννης_00
Επιφανές μέλος
Ο γιαννης_00 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 24 ετών, Φοιτητής του τμήματος Πρόγραμμα Ιερατικών Σπουδών και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 12.981 μηνύματα.

01-10-23

10:58
Ο ευελπις νεος γυμνασμενος και φουσκωμενος και άμυαλος θελει να πηδηξει απο την παραλια αλλα να μην πεσει στην ξερα ...να παει παραπερα
Ας το βοηθησουμε και να του πουμε ποσο φορα πρεπει να παρει...μπας και την γλυτωσει.
Συντακης : Θ.Αλεξοπουλος σεμφε.

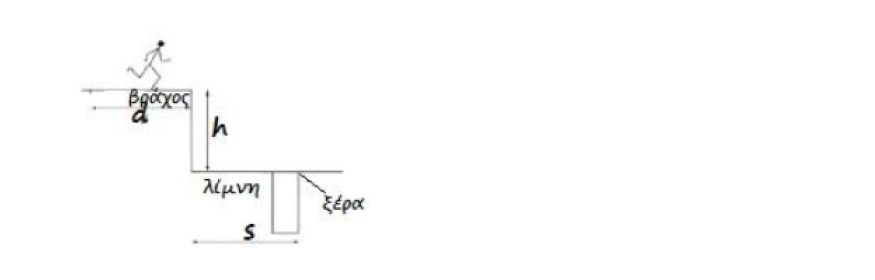
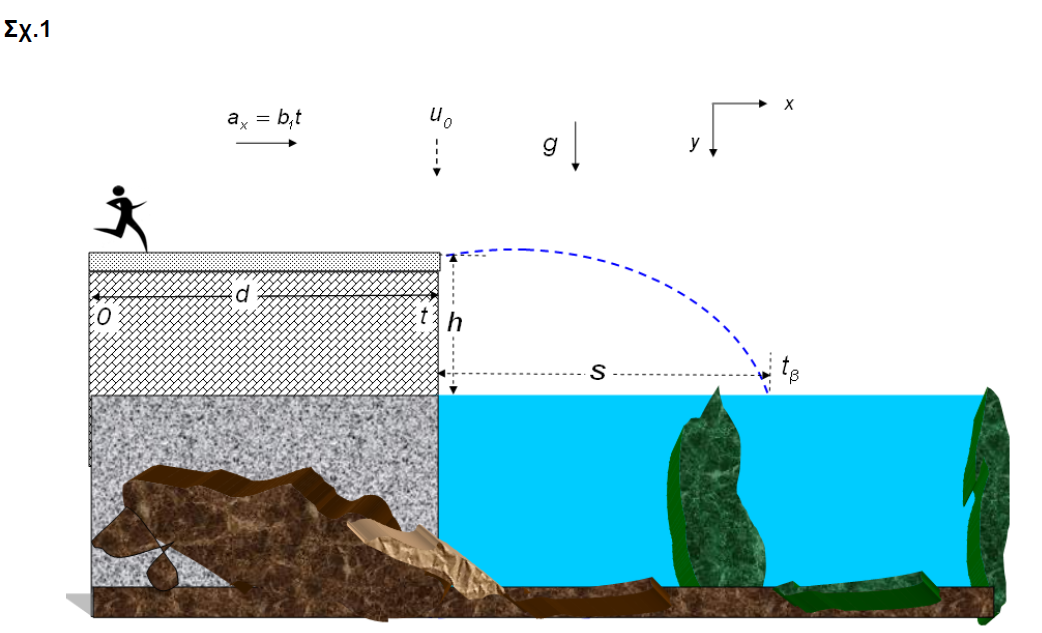


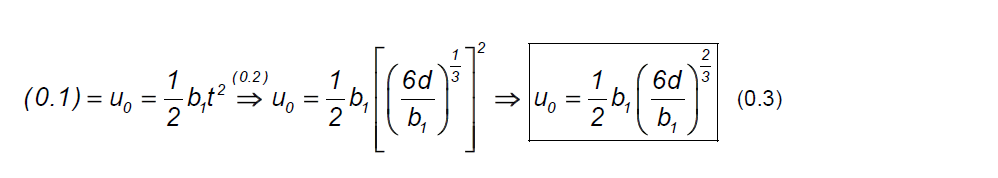


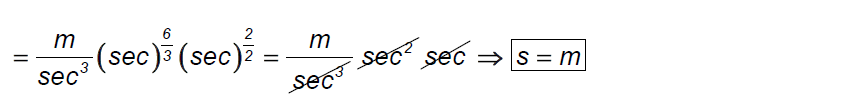
Ωραια τον σωσαμε τον νεο...εμεις θα αλλαζαμε παραλια παντως.
Ας το βοηθησουμε και να του πουμε ποσο φορα πρεπει να παρει...μπας και την γλυτωσει.
Συντακης : Θ.Αλεξοπουλος σεμφε.
Ωραια τον σωσαμε τον νεο...εμεις θα αλλαζαμε παραλια παντως.
γιαννης_00
Επιφανές μέλος
Ο γιαννης_00 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 24 ετών, Φοιτητής του τμήματος Πρόγραμμα Ιερατικών Σπουδών και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 12.981 μηνύματα.

01-10-23

12:39
Εδω εχουμε μια ασκηση που αφιερωνεται στα παιδια του λυκειου που κανουν στερεο και θελουν να σχεδιαζουν τις δρωσες δυναμεις,απλα και ωραια.

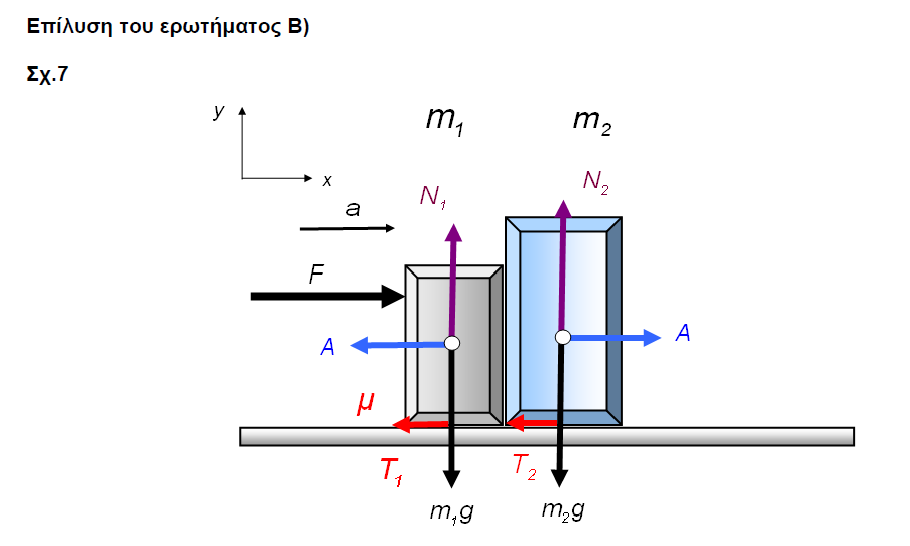

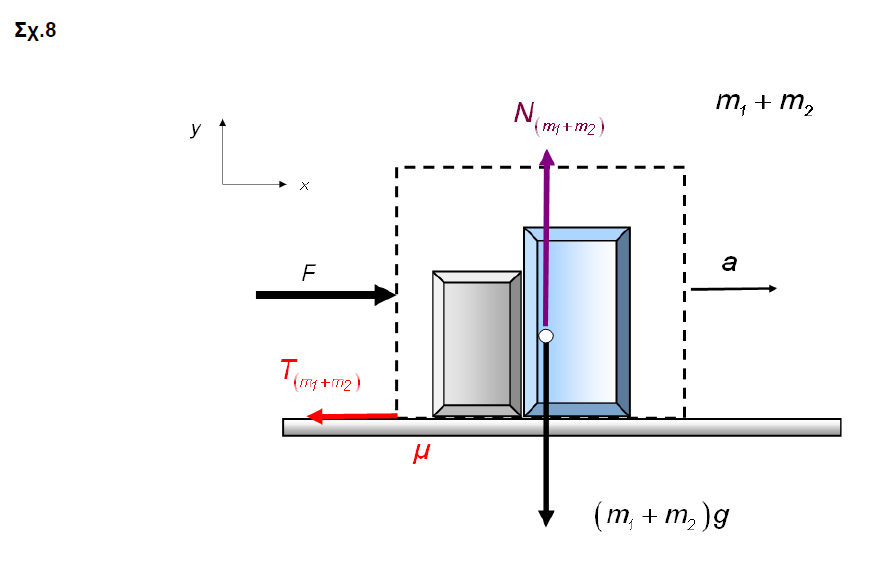




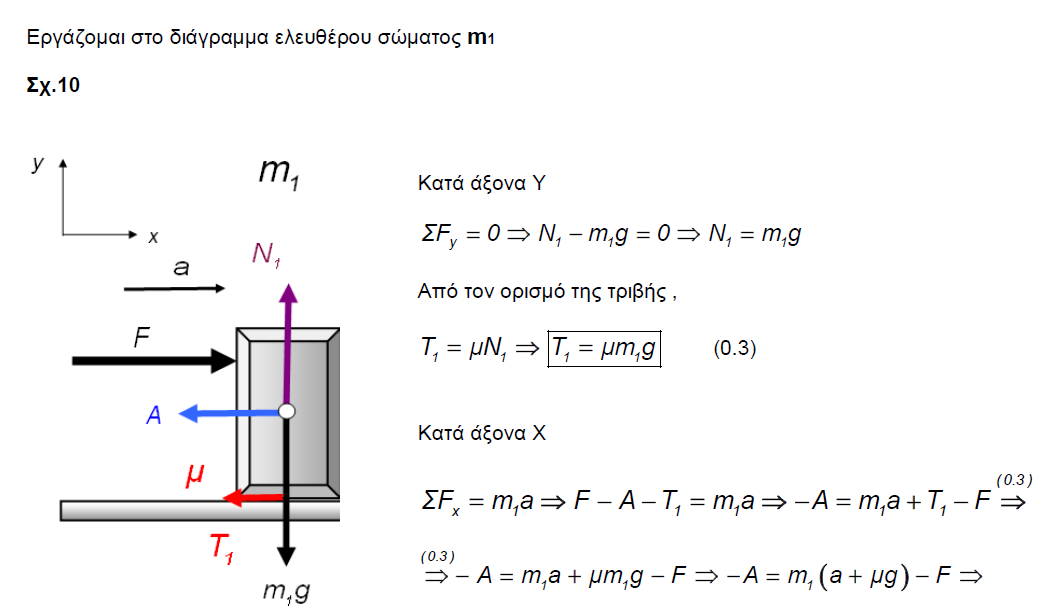

Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 1 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 264 μέλη διάβασαν αυτό το θέμα:
- Chrisphys
- rseven
- Hased Babis
- Debugging_Demon
- tsiobieman
- Hecticism
- andromaxh07
- Unboxholics
- Corfu kitty
- jellojina
- Scandal
- bibliofagos
- Kate1914
- georgetherrr
- antonis97
- Reader
- BatGuin
- thesmilingchild
- iiTzArismaltor_
- Μήτσος10
- Orfano
- charmander
- panosT436
- eirinipap
- exotic xo
- Giorgosvr
- Qwerty 0
- Than003
- angela_k
- Jomo
- Joji
- pnf292
- kost28
- suaimhneas
- Greg25
- redpointer
- Albert.123
- Leo komm
- P.Dam.
- Steliosgkougkou
- chjan
- Evangeloz
- jYanniss
- love_to_learn
- wmaria
- Maynard
- χημεια4λαιφ
- donut_daddy
- marikakitsou16
- physicscrazy
- Lia 2006
- Wonderkid
- chester20080
- panaman
- Msp1
- Sotis
- mirara
- melver
- grad778
- nickd
- V@Per
- sakplat
- ssalex
- despoina13
- catlover033
- carnage
- Μιχαήλ
- eukleidhs1821
- vas2017
- beatrixx
- phleidhs
- gegeorgiou90
- Dr. Gl. Luminous
- agg41
- thepigod762
- Helen06
- Primary Care
- math2arch
- MrDragonboy
- chrismpd
- bill09876
- Paragontas7000
- ikigai
- Marel
- soleilst
- Startx0
- marilenaaa
- EllieKal
- gzois
- akis_95
- EFAKIT
- Φινεύς
- estrela
- Lifelong Learner
- Annie
- Panatha mono
- Mitsaras23
- Isa
- ggl
- BiteTheDust
- Chris180
- aplalew
- user111
- Chemwizard
- giannhs2001
- Mukumbura
- MR WHITE
- SIAmia
- supertom4000
- J.Cameron
- ougkampougka
- persour
- Totreno
- sotirislk
- Specon
- Mariosm.
- Claire05
- Giorgos216
- Jimpower
- shezza94
- kwstasloul
- kan3nas
- dmav
- Obi-Wan Kenobi
- Nancysmilkyway
- Νομάρχης
- ogigidi
- ένας τυχαίος
- Hmmytheos
- constansn
- cannot_log_in
- hello1234
- ilal1200
- Alessandra Eliza
- Giannis327
- phoni
- aggorf
- Nala
- Frozensun
- xrisamikol
- Ilovemycats27
- PanosApo
- nik64
- angies
- dimitris_eee
- mike19
- angeloskar
- eltqt
- CrusaderKingsIII
- flaura
- elevag
- Patroklos
- Anonymous1
- IcedBreaje
- kiyoshi
- nicole1982
- Lost_In_Life
- Γατέχων
- AggelikiGr
- Nansytsg
- Athens2002
- k4t
- Maria_Xagorari
- suuuuiiii
- SoyN
- thecrazycretan
- Jesse_
- A350
- Ιωάννης1234
- george777
- Abiogenesis
- Enhypen
- Mary06
- arko
- Giorgkalo
- velentzakoss
- Giota_pel
- AnnaRd
- Νικολινα
- NikNik1995
- BillyTheKid
- Nick_nt
- a namaves
- xristarac
- ilovekpop
- GeorgePap2003
- Sofos Gerontas
- topg
- Γιώτα Γιαννακού
- plantbee
- Peter Pan13
- Ness
- MrDna
- Jojo K
- Mewmaw
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki

