Βοήθεια/Aπορίες στα Μαθηματικά Προσανατολισμού

P@NT?LO$ · 1 Μαρτίου 2013

Αρχική Δημοσίευση από Sansy16:
Γεια σας λιγη βοηθεια στο υπολογισμο του ολοκληρωματος e^x^2*e^2lnx με ακρα απο το 0 μεχρι το 1 εχω κανει τα παντα και δεν μπορω να βρω αποτελεσμα

εχει ως λυση το e-1?

An $f(x)=\int_{0}^{x}(\int_{0}^{t}{\sigma \upsilon \nu }^{5}u du)dt$ να βρειτε την f''

help SOS

rebel · 28-02-13

https://ischool.e-steki.gr/showthread.php?p=2576616#post2576616

alexandros13 · 28-02-13

rebel · 1 Μαρτίου 2013

Ωραίες ασκήσεις. Νομίζω ότι το κατάλληλο thread γιαυτές θα ήταν η συλλογή της Β' Λυκείου.
1)
Πολλαπλασιάζω την σχέση με $\overrightarrow{A\Gamma}$ (εσωτερικά γινόμενα) και παίρνω
$\left(\overrightarrow{AB}\cdot \overrightarrow{A\Gamma} \right) \overrightarrow{A\Gamma}^2 = \left( \overrightarrow{AM} \cdot \overrightarrow{B \Gamma} \right) \left(\overrightarrow{AB}\cdot \overrightarrow{A\Gamma} \right) \Rightarrow \\ \left(\overrightarrow{A\Gamma}^2 -\overrightarrow{AM} \cdot \overrightarrow{B \Gamma} \right)\overrightarrow{AB}\cdot \overrightarrow{A\Gamma}=0,\,\,(1)$
Όμως
$\overrightarrow{AM} \cdot \overrightarrow{B \Gamma} =\frac{1}{2} \left(\overrightarrow{AB}+\overrightarrow{A\Gamma}\right)\left(\overrightarrow{A\Gamma}-\overrightarrow{AB}\right)=\frac{1}{2} \left(\overrightarrow{A\Gamma}^2-\overrightarrow{AB}^2\right),\,\,(2)$
Αντικαθιστούμε στην (1) και παίρνουμε
$\frac{1}{2}\left(\overrightarrow{A\Gamma}^2+\overrightarrow{AB}^2\right)\overrightarrow{AB}\cdot \overrightarrow{A\Gamma}=0$
και επειδή το $AB\Gamma$ είναι τρίγωνο θα είναι $\overrightarrow{A\Gamma}^2+\overrightarrow{AB}^2 \neq 0$ οπότε $\overrightarrow{AB}\cdot \overrightarrow{A\Gamma} = 0$ και επομένως το τρίγωνο είναι ορθογώνιο με Α γωνία ορθή. Λαμβάνοντας υπ' όψιν αυτό και αντικαθιστώντας την (2) στην δοθείσα σχέση παίρνουμε
$\frac{1}{2}\left(\overrightarrow{A\Gamma}^2-\overrightarrow{AB}^2\right)\overrightarrow{AB}= \vec{0} \Rightarrow \overrightarrow{AB}^2 =\overrightarrow{A\Gamma}^2 \Rightarrow \left|\overrightarrow{AB}\right|= \left|\overrightarrow{A\Gamma} \right|$
άρα αποδείχθηκε και το δεύτερο ζητούμενο.
2)
Αφού $\vec{c}$ και $\vec{b}$ ομόρροπα, θα είναι
$\vec{b} \cdot \vec{c}= \left| \vec{b} \right|\left|\vec{c}\right|,\,\,(3)$
και
$\left|\vec{b}+\vec{c} \right| = \left|\vec{b} \right|+\left|\vec{c} \right|,\,\,(4)$
Από (3),(4) και την δοθείσα ανισότητα έχουμε
$2\left|\vec{b} \right|+2\left|\vec{c} \right|+\left|\vec{c} \right|>6+\left| \vec{b} \right|\left|\vec{c}\right| \Rightarrow \left(2-\left|\vec{c}\right| \right) \left(\left|\vec{b} \right|-3\right)>0$
και το ζητούμενο αποδείχθηκε.
3)
...δεν την είδα αλλά μία σκέψη είναι να υποθέσεις ότι το συμπέρασμα δεν ισχύει και να καταλήξεις σε άτοπο.

MixLazarKal · 01-03-13

Παιδιά Γ'Λυκείου στο 2ο τόμο του Παπαδάκη η 42.54. Λίγη βοήθεια!

IasonasM · 01-03-13

Για το 1) μπορείς επίσης να πεις:
αφού ΑΒ δεν είναι παράλληλο με το ΑΓ (ως πλευρές τριγώνου) τότε ΑΒ*ΑΓ=0 και ΑΜ*ΒΓ=0
(λΑ=κΒ και Α δεν είναι παράλληλο με το Β => λ=0 και κ=0)
από την πρώτη σχέση παίρνεις ότι είναι ορθογώνιο στο Α και από την δεύτερη ότι η διάμεσος ΑΜ είναι και ύψος (κάθετη στο ΒΓ) άρα είναι και ισοσκελές με ΑΒ=ΑΓ.

rebel · 01-03-13

Αρχική Δημοσίευση από IasonasM:
Για το 1) μπορείς επίσης να πεις:
αφού ΑΒ δεν είναι παράλληλο με το ΑΓ (ως πλευρές τριγώνου) τότε ΑΒ*ΑΓ=0 και ΑΜ*ΒΓ=0
(λΑ=κΒ και Α δεν είναι παράλληλο με το Β => λ=0 και κ=0)
από την πρώτη σχέση παίρνεις ότι είναι ορθογώνιο στο Α και από την δεύτερη ότι η διάμεσος ΑΜ είναι και ύψος (κάθετη στο ΒΓ) άρα είναι και ισοσκελές με ΑΒ=ΑΓ.

Έχεις δίκιο! Ταλαιπώρια χωρίς λόγο :wall:

greekgohan · 01-03-13

Αρχική Δημοσίευση από MixLazarKal:
Παιδιά Γ'Λυκείου στο 2ο τόμο του Παπαδάκη η 42.54. Λίγη βοήθεια!

Aξιοποιωντας την συνεχεια θα πρεπει το οριο lim (x+a)/lnx (x τεινει στο 1) να ισουται με το β,αρα το β ειναι 1(κακονας de L'Hospital),συνεπως χ+α=lnx (χ τεινει στο 1).αρα α =-1.
Παιρνωντας τα ορια για να βρεις ασυμπτωτες καταληγεις στο γεγονος οτι δεν υπαρχουν.lim(x-->0)f(x)=0 αρα δεν εχει κατακορυφη,επισης lim(x-->απειρο)f(x)/x=0 και lim(x-->απειρο)f(x)=απειρο
Αρα η cf δεν εχει ασυμπτωτη στο απειρο.

vivianouz · 02-03-13

γεια!!

θα ηθελα αν μπορειτε να με βοηθησετε στις παρακατω:
1)βρειτε συναρτηση f:R->R παραγωγισιμη στο R η οποια ικανοποιει τη σχεση:
$\\ \\ 2\int _{ x }^{ 0 }{ f\left( t \right) } dt=x[xf(x)+2004],\quad x\quad \epsilon \quad \Re \\ \\$

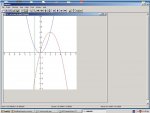
2)να βρεθει το εμβαδον του χωριου Ω που περικλειεται απο τις γραφικες παραστασεις των συναρτησεων f(x)=(x^2),g(x)=4x-(x^2) και την ευθεια χ=-1

P@NT?LO$ · 02-03-13

Ασκηση 18 σελ.330 Μπαρλας β τευχος
Εστω $f:R\rightarrow R$ μια αντιστρεψιμη και παραγωγισιμη συναρτηση με $f(0)=0$ . Να δειξετε οτι $\int_{0}^{x}f(t)dt + \int_{0}^{f(x)}{f}^{-1}(t)dt=xf(x)$ για καθε $x\varepsilon R$

Ασκηση 35 σελ.332 Μπαρλας β τευχος
Να βρειτε τη συναρτηση $f:\left(1,+\propto \right)$ με f'' συνεχη για την οποια ισχυουν $f(e)=0$ $f'(e)={e}^{-1}$ και $\int_{e}^{x}f''(t)lntdt=\frac{1}{x}-\int_{e}^{x}\frac{1}{t}f'(t)dt - \frac{1}{e}$ , $x>1$

ΒΟΗΘΕΙΑ

lowbaper92 · 02-03-13

Αρχική Δημοσίευση από P@NT?LO$:
Ασκηση 35 σελ.332 Μπαρλας β τευχος
Να βρειτε τη συναρτηση $f:\left(1,+\propto \right)$ με f'' συνεχη για την οποια ισχυουν $f(e)=0$ $f'(e)={e}^{-1}$ και $\int_{e}^{x}f''(t)lntdt=\frac{1}{x}-\int_{e}^{x}\frac{1}{t}f'(t)dt - \frac{1}{e}$ , $x>1$

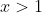
Φέρνω τα ολοκληρώματα στο πρώτο μέλος, κι επειδή έχουν τα ίδια όρια ολοκλήρωσης, τα βάζω σε κοινό ολοκλήρωμα:

$\int_{e}^{x}\left[f''\left(t \right)lnt+\frac{1}{t}f'\left(t \right) \right]dt=\frac{1}{x}-\frac{1}{e}\Leftrightarrow \int_{e}^{x}\left[\left(f'\left(t \right) \right)'lnt+f'\left(t \right)\left(lnt \right)' \right]dt=\frac{1}{x}-\frac{1}{e}\Leftrightarrow \int_{e}^{x}\left[f'\left(t \right)lnt \right]'dt=\frac{1}{x}-\frac{1}{e}\Leftrightarrow \left[f'\left(t \right) lnt\right]{}^{x}{}_{e}=\frac{1}{x}-\frac{1}{e}\Leftrightarrow f'\left(x \right)lnx-\frac{1}{e}=\frac{1}{x}-\frac{1}{e}\Leftrightarrow f'\left(x \right)lnx=\left(lnx \right)'\stackrel{lnx>0 \, \forall x>1}{\Leftrightarrow \Leftrightarrow\Leftrightarrow } f'\left(x \right)=\frac{\left(lnx \right)'}{lnx}\Leftrightarrow f\left(x \right)=ln\left(lnx \right)+c$

Για x=e προκύπτει c=0

Άρα τελικά $f\left(x \right)=ln\left(lnx \right),\; x\in \left(1,+\infty \right)$

rebel · 2 Μαρτίου 2013

Αρχική Δημοσίευση από P@NT?LO$:
Ασκηση 18 σελ.330 Μπαρλας β τευχος
Εστω $f:R\rightarrow R$ μια αντιστρεψιμη και παραγωγισιμη συναρτηση με $f(0)=0$ . Να δειξετε οτι $\int_{0}^{x}f(t)dt + \int_{0}^{f(x)}{f}^{-1}(t)dt=xf(x)$ για καθε $x\varepsilon R$

Στο δεύτερο ολοκλήρωμα αλλαγή μεταβλητής $u=f^{-1}(t)$ , μετά παραγοντική ολοκλήρωση και βγαίνει.

Αρχική Δημοσίευση από vivianouz:
2)να βρεθει το εμβαδον του χωριου Ω που περικλειεται απο τις γραφικες παραστασεις των συναρτησεων f(x)=(x^2),g(x)=4x-(x^2) και την ευθεια χ=-1

$f(x)=g(x) \Leftrightarrow 2x(x-2)=0 \Leftrightarrow x=0 \,\,\acute{\eta}\,\,x=2$
Για $-1 \leq x \leq 0$ είναι $f(x) \geq g(x)$ οπότε το εμβαδόν είναι
$\int_{-1}^0 \left(f(x)-g(x) \right) dx$

vimaproto · 02-03-13

Ποιο είναι το Ω?

rebel · 3 Μαρτίου 2013

Πράγματι είναι ασαφές, όμως σε τέτοιες περιπτώσεις πιστεύω ότι αν θεωρήσει κανείς το χωρίο από την ευθεία που μας δίνει μέχρι την πλησιέστερη ρίζα της $f(x)-g(x)=0$ είναι εντάξει. Ας θυμηθούμε άλλωστε και το θέμα Γ4 των περσινών πανελληνίων που ζητούσε το εμβαδόν του χωρίου που περικλείεται από την γραφική παράσταση της $g(x)=(x-1) \ln x$ την ευθεία $x=e$ και τον άξονα $x'x$ . Όπως βλέπουμε και στο σχήμα, το αριστερό όριο του χωρίου είναι ακαθόριστο, όμως σε όλες τις λύσεις που κυκλοφόρησαν θεωρήθηκε σωστό το
$E=\int_{1}^e g(x) dx$

P@NT?LO$ · 03-03-13

Εστω $f:R\rightarrow R$ μια συναρτηση για την οποια ισχυει $f(x)=\frac{1}{2}\int_{0}^{-f(x)}\eta \mu {t}^{2}dt$ για καθε x που ανηκει στο R.Να δειξετε οτι $f(x)=0$

Εστω μια παραγωγισιμη συναρτηση $f:[0,+\propto )\rightarrow R$ για την οποια ισχυει $xf'(x)=f(x) + \int_{0}^{1}f(t)dt$ , $x\geq 0$ Αν $f(0)=1$ να βρειτε τον τυπο της f

MixLazarKal · 03-03-13

Ευτυχώς πρόλαβα και το έλυσα πριν δω την απάντησή σου. Και τελικά συμφωνούμε! Σε ευχαριστώ!

Solmyr · 03-03-13

Αρχική Δημοσίευση από P@NT?LO$:
Εστω μια παραγωγισιμη συναρτηση $f:[0,+\propto )\rightarrow R$ για την οποια ισχυει $xf'(x)=f(x) + \int_{0}^{1}f(t)dt$ , $x\geq 0$ Αν $f(0)=1$ να βρειτε τον τυπο της f

Η άσκηση αυτή είναι καλή.Λοιπόν εγώ θα σου πω απλά τον τρόπο.Θα θέσεις το ολοκλήρωμα με άκρα ένα γράμμα έστω c(αφού το ολοκλήρωμα με άκρα είναι ουσιαστικά 1 αριθμός ότι και να έχει μέσα).Ύστερα στη δοθείσα σχέση θα λύσεις ως προς f(x).Δηλαδή f(x)=xf'(x) - c.Αυτό θα το αντικαταστήσεις στη συνάρτηση που έθεσες.Από εκεί θα βρεις μια σχέση με το c.

Έπειτα στην αρχική σχέση θα κάνεις <<αντιπαραγώγιση>> και θα δεις που θα σε πάει η άσκηση...

exc · 03-03-13

Αρχική Δημοσίευση από P@NT?LO$:
Εστω $f:R\rightarrow R$ μια συναρτηση για την οποια ισχυει $f(x)=\frac{1}{2}\int_{0}^{-f(x)}\eta \mu {t}^{2}dt$ για καθε x που ανηκει στο R.Να δειξετε οτι $f(x)=0$

Λοιπόν, για μία μη μηδενική συνάρτηση g(x), το $\frac{1}{b-a}\int_a^b g(x) \text{dx}$ είναι η μέση τιμή της συνάρτησης στο [a,b]. Για μία συνεχή μη μηδενική g(x), είναι προφανές ότι θα υπάρχει μία τιμή έστω ξ που θα ανήκει στο [a,b] η οποία θα παίρνει την την μέση τιμή της. Η για να το πω με μαθηματικά, θα υπάρχει $\xi\in[a,b]: \frac{1}{b-a}\int_a^b g(x) \text{dx}=g(\xi)(*)$ .

Εν προκειμένω έχουμε:
$f(x)=\frac{1}{2}\int_0^{-f(x)}\sin t^2\text{dt}=\frac{1}{2}\sin\xi^2(-f(x))\Leftrightarrow \\\Leftrightarrow f(x)(1+\frac{1}{2}\sin\xi^2)=0 \text{,\,\,for\,a\,\,\,} \xi\in (-\infty,+\infty)(**)}$
To οποίο συμβαίνει μόνο όταν f(x)=0.

Σημ.:
$(*)$ Αυτό ίσως το έχεις συναντήσει ως το ΘΜΤ του ολοκληρωτικού λογισμού.
$(**)f:\mathbb{R}\to\mathbb{R}\Rightarrow [0,-f(x)]\to (-\infty,+\infty)$

rebel · 3 Μαρτίου 2013

Αρχική Δημοσίευση από P@NT?LO$:
Εστω $f:R\rightarrow R$ μια συναρτηση για την οποια ισχυει $f(x)=\frac{1}{2}\int_{0}^{-f(x)}\eta \mu {t}^{2}dt$ για καθε x που ανηκει στο R.Να δειξετε οτι $f(x)=0$

$-1 \leq \eta \mu \left(t^2\right) \leq 1 \Rightarrow -\int_0^{-f(x)}1 dt \leq \int_{0}^{-f(x)}\eta \mu \left(t^2\right) dt \leq \int_0^{-f(x)}1 dt \Rightarrow -\left(-f(x)\right) \leq 2f(x) \leq -f(x) \Rightarrow 0 \leq f(x) \leq 0 \Rightarrow f(x)=0,\,\,\forall x \in \mathbb{R}$

P@NT?LO$ · 03-03-13

Αρχική Δημοσίευση από exc:
Λοιπόν, για μία μη μηδενική συνάρτηση g(x), το $\frac{1}{b-a}\int_a^b g(x) \text{dx}$ είναι η μέση τιμή της συνάρτησης στο [a,b]. Για μία συνεχή μη μηδενική g(x), είναι προφανές ότι θα υπάρχει μία τιμή έστω ξ που θα ανήκει στο [a,b] η οποία θα παίρνει την την μέση τιμή της. Η για να το πω με μαθηματικά, θα υπάρχει $\xi\in[a,b]: \frac{1}{b-a}\int_a^b g(x) \text{dx}=g(\xi)(*)$ .

Εν προκειμένω έχουμε:
$f(x)=\frac{1}{2}\int_0^{-f(x)}\sin t^2\text{dt}=\frac{1}{2}\sin\xi^2(-f(x))\Leftrightarrow \\\Leftrightarrow f(x)(1+\frac{1}{2}\sin\xi^2)=0 \text{,\,\,for\,a\,\,\,} \xi\in (-\infty,+\infty)(**)}$
To οποίο συμβαίνει μόνο όταν f(x)=0.

Σημ.:
$(*)$ Αυτό ίσως το έχεις συναντήσει ως το ΘΜΤ του ολοκληρωτικού λογισμού.
$(**)f:\mathbb{R}\to\mathbb{R}\Rightarrow [0,-f(x)]\to (-\infty,+\infty)$

ΤΡΟΜΑΞΑ ΡΕ ΦΙΛΕ..

ευχαριστω παντως...

Βοήθεια/Aπορίες στα Μαθηματικά Προσανατολισμού

Νεοφερμένος

Πολύ δραστήριο μέλος

Νεοφερμένος

Πολύ δραστήριο μέλος

Νεοφερμένος

Εκκολαπτόμενο μέλος

Πολύ δραστήριο μέλος

Εκκολαπτόμενο μέλος

Νεοφερμένος

Νεοφερμένος

Πολύ δραστήριο μέλος

Πολύ δραστήριο μέλος

Πολύ δραστήριο μέλος

Συνημμένα

Πολύ δραστήριο μέλος

Νεοφερμένος

Νεοφερμένος

Δραστήριο μέλος

Διάσημο μέλος

Πολύ δραστήριο μέλος

Νεοφερμένος