
21-02-13

18:40
Δεν καναμε ακομα το κεφαλαιο αυτο η απορια μου ειναι απτα αρχικα που λεει οτι παντα αν f(x)>0 υπαρχει περιπτωση να μην εχουμε απολυτα και να ειναι μια συναρτηση αρντικη σε ενα διαστημα και συνεχης εκει το ολοκληρωμα της παλι θα δειχνει εμβαδον ακομα και αν g(x)<0
σχολικο σελ 330 στο τελευταιο αποσπασμα
Πάντως έτσι όπως τα λες, ούτε εγώ καταλαβαίνω τι εννοείς.
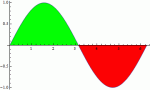
Κοίτα το συνημμένο. Είναι μία συνάρτηση ημιτόνου.
Μέχρι το π είναι θετική. Εκεί ο ολοκλήρωμα από 0 έως π θα δώσει μία θετική τιμή (2). 2 είναι το εμβαδόν που περικλείεται μεταξύ της καμπύλης και του άξονα των x.
Από π έως 2π, η συνάρτηση είναι αρνητική και εκεί το ολοκλήρωμα θα δώσει -2. Το |-2|=2 μα δίνει το εμβαδόν της καμπύλης σε εκείνη την περιοχή, ενώ το πλην μας λέει ότι βρίσκεται από κάτω.
Αν ολοκληρώσεις σε διάστημα που είναι μία θετική και μία αρνητική, τότε ουσιαστικά προσθέτεις το εμβαδόν των περιοχών που είναι θετική και αφαιρείς το εμβαδόν στις περιοχές που είναι αρνητική. Αν το αποτέλεσμα είναι θετικό, τότε περισσότερο εμβαδόν βρίσκεται από πάνω, αν είναι αρνητικό περισσότερο βρίσκεται από κάτω, ενώ αν είναι 0, τότε είναι ίσα.
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki



 ) ότι e^g(x)=e^(x+lnx)=x*e^x=f(g(x)), άρα f(x)=e^x.
) ότι e^g(x)=e^(x+lnx)=x*e^x=f(g(x)), άρα f(x)=e^x.
