Βοήθεια/Aπορίες στα Μαθηματικά Προσανατολισμού

exc · 21-02-13

Αρχική Δημοσίευση από Sansy16:
Δεν καναμε ακομα το κεφαλαιο αυτο η απορια μου ειναι απτα αρχικα που λεει οτι παντα αν f(x)>0 υπαρχει περιπτωση να μην εχουμε απολυτα και να ειναι μια συναρτηση αρντικη σε ενα διαστημα και συνεχης εκει το ολοκληρωμα της παλι θα δειχνει εμβαδον ακομα και αν g(x)<0

Αρχική Δημοσίευση από Sansy16:
σχολικο σελ 330 στο τελευταιο αποσπασμα

Πάντως έτσι όπως τα λες, ούτε εγώ καταλαβαίνω τι εννοείς.

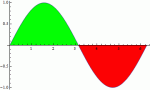
Κοίτα το συνημμένο. Είναι μία συνάρτηση ημιτόνου.
Μέχρι το π είναι θετική. Εκεί ο ολοκλήρωμα από 0 έως π θα δώσει μία θετική τιμή (2). 2 είναι το εμβαδόν που περικλείεται μεταξύ της καμπύλης και του άξονα των x.

Από π έως 2π, η συνάρτηση είναι αρνητική και εκεί το ολοκλήρωμα θα δώσει -2. Το |-2|=2 μα δίνει το εμβαδόν της καμπύλης σε εκείνη την περιοχή, ενώ το πλην μας λέει ότι βρίσκεται από κάτω.

Αν ολοκληρώσεις σε διάστημα που είναι μία θετική και μία αρνητική, τότε ουσιαστικά προσθέτεις το εμβαδόν των περιοχών που είναι θετική και αφαιρείς το εμβαδόν στις περιοχές που είναι αρνητική. Αν το αποτέλεσμα είναι θετικό, τότε περισσότερο εμβαδόν βρίσκεται από πάνω, αν είναι αρνητικό περισσότερο βρίσκεται από κάτω, ενώ αν είναι 0, τότε είναι ίσα.

t00nS · 21-02-13

Αρχική Δημοσίευση από t00nS:
έστω f(0,+oo)->R μια συνάρτηση με f(1)=0 καi f(τόνος)(χ)>1 +lnx, για κάθε χ>0
1)Να δείξετε ότι:
f(x)<xlnx,για κάθε χε(0,1),f(x)>xlnx για κάθε χ>1 και μετά να λύσετε την εξίσωση f(x)=0
2)να βρείτε τα όρια lim(x->+oo)f(x),lim(x->+oo) f(x)-λ-χ/χ
3)να δείξετε ότι υπάρχει ξε(1,2)τέτοιο ώστε f(τόνος)(ξ)>ln2
βρήκα το πρώτο αλλά δεν είμαι σίγουρος

αν γίνετε μια βοήθεια σε αυτή

exc · 21-02-13

Αρχική Δημοσίευση από t00nS:
αν γίνετε μια βοήθεια σε αυτή

Υποδείξεις:
1) Πάρε ορισμένο ολοκλήρωμα από x έως 1 της ανισότηττας με την παράγωγο.
Μετά πάρε από 1 έως x.
Τη λύση της ξέρεις. Δείξε τη μοναδικότητα βρίσκοντας την μονοτονία από τις ανισότητες.
2) Χρησιμοποίησε τις ανισότητες. Το πρώτο βγαίνει σχεδόν άμεσα. Στο δεύτερο δεν καταλαβαίνω τι έχεις γράψει, αλλά θα βγαίνει και αυτό εύκολα.
3) Χρησιμοποίησε την ανισότητα. Βγαίνει άμεσα.

rebel · 22 Φεβρουαρίου 2013

α)
Θεωρούμε $g(x)=f(x)- x \ln x$ με $g'(x)=f'(x)-\ln x-1>0,\,\,x>0$ άρα g γνησίως αύξουσα οπότε $g(x)<g(1) \Leftrightarrow f(x)< x \ln x$ για χ<1 και $g(x)>g(1) \Leftrightarrow f(x) > x \ln x$ για χ>1.

Επίσης για χ>1 είναι $f(x)>x \ln x>0$ αφού $\ln x>0$ και για 0<χ<1 είναι $f(x)<x \ln x<0$ αφού $\ln x<0$ . Άρα μοναδική λύση η $x=1$

β)
Για μεγάλο χ είναι $f(x)> x \ln x$ και επειδή $\lim_{x \to +\infty}x \ln x = +\infty$ είναι $\lim_{x \to +\infty}f(x) = +\infty$

$\frac{f(x)- \lambda - x}{x} =\frac{f(x)}{x}- \frac{\lambda}{x}-1$
με
$\frac{f(x)}{x}> \ln x$ άρα $\lim_{x \to +\infty}\frac{f(x)}{x} = +\infty$ αφού $\lim_{x \to +\infty} \ln x = +\infty$
άρα το δεύτερο όριο κάνει $+\infty$
γ)
Από ΘΜΤ υπάρχει $\xi \in (1,2)$ με $f'(\xi)=\frac{f(2)-f(1)}{2-1}=f(2)>2 \ln2> \ln2$
και το ζητούμενο αποδείχθηκε.
H ποιο απλά έστω $\xi \in (1,2)$ αυθαίρετο. Τότε
$f'(\xi)>1+\ln \xi >1+\ln 1=1=\ln e > \ln 2$

P@NT?LO$ · 21-02-13

Αν η συναρτηση f exei f'' συνεχη στο [0,1] και ειναι f(0)=1 , f(1)=f'(0)=f'(1)=0 να υπολογισετε το ολοκληρωμα $I=\int_{0}^{1}\frac{f''(x)-f(x)}{{e}^{x}}dx$
ας την λυσει καποιος παρακαλω...
και επισης μια βοηθεια.. τι να θεσω ως u σε αυτο? $\int_{\frac{1}{2}}^{2}\frac{{x}^{2}-1}{{x}^{2}}{e}^{x+\frac{1}{x}}dx$

rebel · 21-02-13

Για το πρώτο παρατήρησε ότι
$\frac{f''(x)-f(x)}{e^x}=\frac{f''(x)-f'(x)}{e^x}+\frac{f'(x)-f(x)}{e^x}= \\ \frac{f''(x)e^x-f'(x)e^x}{e^{2x}}+\frac{f'(x)e^x-f(x)e^x}{e^{2x}} = \left( \frac{f'(x)}{e^x} \right)'+ \left( \frac{f(x)}{e^x} \right)'= \left( \frac{f(x)+f'(x)}{e^x} \right)'$
Για το δεύτερο βρες την
$\left( e^{x+ \frac{1}{x}} \right)'$
Τι παρατηρείς;

P@NT?LO$ · 21-02-13

ωραιος να σαι καλα... 0 δεν βγαινει το δευτερο ή εχω κανει λαθος??

rebel · 21-02-13

0 ναι.

vimaproto · 22-02-13

Ευφυέστατες οι λύσεις σου Κώστα , αλλά εγώ θα ακολουθήσω τα ...κλασσικά.
Στην (1) κατά παράγοντες και στη (2) αντικατάσταση [Ξέχνα και το latex γιατί θα βραδιάσω]

Sansy16 · 22 Φεβρουαρίου 2013

Αρχική Δημοσίευση από styt_geia:
Σου εξήγησα τι δηλώνει το ολοκλήρωμα αν η συνάρτηση είναι αρνητική στο διάστημα [α,β] αν και το πήγα δια της πλαγίας οδού. Είναι το -(εμβαδόν Ω). Για ποιο απόσπασμα λες ακριβώς, γιατί δεν καταλαβαίνω; Σε ποια σελίδα;

Αρχική Δημοσίευση από exc:
Πάντως έτσι όπως τα λες, ούτε εγώ καταλαβαίνω τι εννοείς.

Κοίτα το συνημμένο. Είναι μία συνάρτηση ημιτόνου.
Μέχρι το π είναι θετική. Εκεί ο ολοκλήρωμα από 0 έως π θα δώσει μία θετική τιμή (2). 2 είναι το εμβαδόν που περικλείεται μεταξύ της καμπύλης και του άξονα των x.

Από π έως 2π, η συνάρτηση είναι αρνητική και εκεί το ολοκλήρωμα θα δώσει -2. Το |-2|=2 μα δίνει το εμβαδόν της καμπύλης σε εκείνη την περιοχή, ενώ το πλην μας λέει ότι βρίσκεται από κάτω

Αν ολοκληρώσεις σε διάστημα που είναι μία θετική και μία αρνητική, τότε ουσιαστικά προσθέτεις το εμβαδόν των περιοχών που είναι θετική και αφαιρείς το εμβαδόν στις περιοχές που είναι αρνητική. Αν το αποτέλεσμα είναι θετικό, τότε περισσότερο εμβαδόν βρίσκεται από πάνω, αν είναι αρνητικό περισσότερο βρίσκεται από κάτω, ενώ αν είναι 0, τότε είναι ίσα.

Ναι αυτο ηθελα ουσιαστικα η απορια μου ηταν τι δειχνει το ολοκληρωμα οταν στο διαστημα που παιρνουμε ολοκληρωμα ισχυει f(x)<0 δηαδη παλι το εβαδον της f με καλυψατε εχυαριστω πολυ

Mercury · 24-02-13

Απο το βιβλίο του Μπάρλα,τεύχος πρώτο,σελίδα 67 άσκηση 72:
Να βρείτε τους γεωμετρικούς τόπους των εικονων των μιγαδικών z και w για τους οποίους ισχύουν:
$\left|z-1 \right|=\left|iz+1 \right|$
$w=\lambda (1+i)+2i$

Βρίσκω ότι για το z είναι y=x και για τον w β=α+2

Μετά να δείξετε ότι
$\left|z-w \right|\geq 2$
Καταλαβαινω πως είναι η απόσταση μεταξύ των μιγαδικών...Αλλά πώς θα το βρώ; :hmm:

lowbaper92 · 25-02-13

Αρχική Δημοσίευση από Mercury:
Απο το βιβλίο του Μπάρλα,τεύχος πρώτο,σελίδα 67 άσκηση 72:
Να βρείτε τους γεωμετρικούς τόπους των εικονων των μιγαδικών z και w για τους οποίους ισχύουν:
$\left|z-1 \right|=\left|iz+1 \right|$
$w=\lambda (1+i)+2i$

Βρίσκω ότι για το z είναι y=x και για τον w β=α+2

Μετά να δείξετε ότι
$\left|z-w \right|\geq 2$
Καταλαβαινω πως είναι η απόσταση μεταξύ των μιγαδικών...Αλλά πώς θα το βρώ;

Μήπως λέει $\sqrt{2}$ ?

Καταρχάς, η ελάχιστη απόσταση δύο παράλληλων ευθειών ισούται με το μήκος της κοινής τους καθέτου.
Δεύτερον, η απόσταση των δύο παράλληλων ευθειών ε1 (y=x) και ε2 (y=x+2), ισούται με την απόσταση ενός σημείου της ε1, με την ε2. Ας θεωρήσουμε το Ο(0,0) για να βολεύουν και οι πράξεις.

${d}_{min}\left({\varepsilon }_{1},{\varepsilon }_{2} \right)=d\left(O,{\varepsilon }_{2} \right)=\frac{1\cdot 0+\left(-1 \right)\cdot 0+2}{\sqrt{{1}^{2}+{\left(-1 \right)}^{2}}}=\sqrt{2}$

Mercury · 25-02-13

Ναι ναι...σορρυ δικό μου λάθος.
Το έλυσα λιγάκι αργότερα τελικά,με το ίδιο ακριβώς τρόπο που έλυσε και εσύ.
Θένκς!

P@NT?LO$ · 25-02-13

Εστω μια συνεχης συναρτηση $f:R\rightarrow R$ και η $g(x)=x+lnx$ (ειναι γν.ΑΥΞ και 1-1) με $f(g(x))=x{e}^{x}$ ,x>0
Να υπολογισετε το ολοκληρωμα $\int_{1}^{1+e}f(x)dx$

rebel · 25-02-13

Με αλλαγή μεταβλητής γίνεται
$\int_1^{1+e} \! f(x) \, \mathrm{d}x= \int_{g^{-1}(1)}^{g^{-1}(1+e)} \! f \left( g(u) \right) g'(u) \, \mathrm{d}u$
κλπ

exc · 25-02-13

Αρχική Δημοσίευση από P@NT?LO$:
Εστω μια συνεχης συναρτηση $f:R\rightarrow R$ και η $g(x)=x+lnx$ (ειναι γν.ΑΥΞ και 1-1) με $f(g(x))=x{e}^{x}$ ,x>0
Να υπολογισετε το ολοκληρωμα $\int_{1}^{1+e}f(x)dx$

Παρατηρώ (

) ότι e^g(x)=e^(x+lnx)=x*e^x=f(g(x)), άρα f(x)=e^x.

P@NT?LO$ · 25-02-13

απο το e^(x+lnx) πως πας στο x*e^x??

exc · 25-02-13

Αρχική Δημοσίευση από P@NT?LO$:
απο το e^(x+lnx) πως πας στο x*e^x??

Είναι ιδιότητα της εκθετικής: exp(a+b)=exp(a)*exp(b).

P@NT?LO$ · 25-02-13

α οκ ευχαριστω και τους 2 σας μαγκες...να στε καλα...

P@NT?LO$ · 25-02-13

Εστω μια συναρτηση f με f(1)=1 , η οποια ειναι 2 φορες παραγωγισιμη στο [0,2] και ισχυει $f''(x)=-f''(2-x)$ για καθε $x\epsilon \left[0,2 \right]$
Να υπολογισετε το ολοκληρωμα $\int_{0}^{2}f(x)dx$

Η τελευταια ασκηση που μου μενει απο τις 13 που εχω για αυριο το απογευμα ειναι και εχω ξενερωσει που δεν μπορω να τη λυσω.... ΒΟΗΘΕΙΑ!!!

Βοήθεια/Aπορίες στα Μαθηματικά Προσανατολισμού

Διάσημο μέλος

Συνημμένα

Εκκολαπτόμενο μέλος

Διάσημο μέλος

Πολύ δραστήριο μέλος

Νεοφερμένος

Πολύ δραστήριο μέλος

Νεοφερμένος

Πολύ δραστήριο μέλος

Πολύ δραστήριο μέλος

Συνημμένα

Νεοφερμένος

Επιφανές μέλος

Πολύ δραστήριο μέλος

Επιφανές μέλος

Νεοφερμένος

Πολύ δραστήριο μέλος

Διάσημο μέλος

Νεοφερμένος

Διάσημο μέλος

Νεοφερμένος

Νεοφερμένος