Λοιπόν...νέες απορίες(μπόλικες)
Ξεκινάμε...
Μαθηματικά του Μπάρλα,τεύχος πρώτο,
Σελίδα 65 ασκηση 56:
Έστω
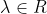
και ο μιγαδικός z για τον οποίο ισχύει \lambda z+\bar{z}=\left|z \right|
Να δείξετε ότι λ=1
Σελιδα 65 άσκηση 59.
Έστω έ η ευθεία που ορίζουν οι εικόνες των μιγαδικών
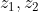
στο μιγαδικό επίπεδο για τους οποίους ισχύει:
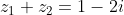
και
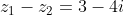
Να βρείτε το μιγαδικό w που η εικόνα του βρίσκεται στην ευθεία και έχει το μικρότερο δυνατό μέτρο.
Εδώ βρίσκω τους μιγαδικούς,καταφέρνω να βρώ να την εξίσωση ευθείας,αλλά μετά κολλάω...
Σελίδα 66 ασκηση 63
Έστω
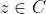
με
z+2i \right|2)
i)Να βρείτε το γεωμετρικό τόπο των σημειων Μ(z) για τα οποία ισχύει η παραπάνω σχέση.(αυτό το έλυσα)
ii)Να βρείτε το γεωμετρικό τόπο των σημείων Ν(w) για τα οποία ισχύει wz=1 (εδώ πρέπει να έχει να κάνει με αντίστροφο του z σωστα; )
Σελιδα 66 ασκηση 66
Αν η εικόνα του μιγαδικού z ανήκει στον κύκλο κέντρου Κ(0,2) και ακτίνας ρ=1 να βρείτε που ανήκει η εικόνα του
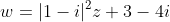
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki

