JKaradakov
Τιμώμενο Μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
bond_bill
Νεοφερμένο μέλος


Αν η f εχει ελαχιστο τοτε f(x)>=0 συνεπαγεται minf>=o
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Aris90
Εκκολαπτόμενο μέλος


Δινεται η συναρτηση
Να βρεθει η τιμη του α ωστε να ειναι
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Αντίστροφα αν
με
απ' όπου βλέπουμε εύκολα ότι
κι έτσι πράγματι η
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Mercury
Επιφανές μέλος


Δίνεται:
και
Να βρεθεί ο γεωμετρικός τόπος του z.
Λύση:
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
JKaradakov
Τιμώμενο Μέλος


Χρειάζομαι μία επαλήθευση:
Δίνεται:
και
Να βρεθεί ο γεωμετρικός τόπος του z.
Λύση:
Σωστό είναι.
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
tweetyslvstr
Δραστήριο μέλος


Δίνεται εξισωση χ2-ψ2+6χ+9=0(σημ. όπου 2 είναι στο τετραγωνο αλλά δεν μπορώ να το βάλω)
α). Να δείξετε ότι η παραπάνω εξίσωση παριστάνει δύο ευθείες ε1 και ε2
β). Να δείξετε ότι οι ευθείες είναι κάθετες.
γ) Να βρείτε ένα σημείο Μ(κ.λ) με κ>0 και λ>0 τέτοιο, ώστε το διάνυσμα α=(3,κ) να είναι παράλληλο προς τη μια από τις δύο ευθείες ε1 και ε2 και το διάνυσμα β(-16,4λ) να είναι παράλληλο προς την άλλη ευθεία.
δ) Ν γράψετε την εξίσωση της παραβολής που έχει κορυφη την αρχή των αξόνων Ο, άξονα συμμετρίας τον άξονα χ'χ και διερχεται από το σημείο Μ.
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
vimaproto
Πολύ δραστήριο μέλος


Καλησπερα. Επειδή βρήκα μια άσκηση στις ευθείες στο βοήθημα του κ. Μπάρλα και δεν μπορώ να την λύσω θα μπορούσατε να μου πείτε τον τρόπο λύσης? Λοιπόν η ασκηση έχει ως εξής
Δίνεται εξισωση χ2-ψ2+6χ+9=0(σημ. όπου 2 είναι στο τετραγωνο αλλά δεν μπορώ να το βάλω)
α). Να δείξετε ότι η παραπάνω εξίσωση παριστάνει δύο ευθείες ε1 και ε2
β). Να δείξετε ότι οι ευθείες είναι κάθετες.
γ) Να βρείτε ένα σημείο Μ(κ.λ) με κ>0 και λ>0 τέτοιο, ώστε το διάνυσμα α=(3,κ) να είναι παράλληλο προς τη μια από τις δύο ευθείες ε1 και ε2 και το διάνυσμα β(-16,4λ) να είναι παράλληλο προς την άλλη ευθεία.
δ) Ν γράψετε την εξίσωση της παραβολής που έχει κορυφη την αρχή των αξόνων Ο, άξονα συμμετρίας τον άξονα χ'χ και διερχεται από το σημείο Μ.
Τόσες φορές το είπε ο Δίας σε ελληνικό πληκτρολόγιο Ctrl+Alt+2=² Ctrl+Alt+3=³ Και εγώ δεν τα ήξερα αλλά τα έμαθα
Στο θέμα μας τώρα.
α) χ²+6χ+9-y²=0 ==> (χ+3)²-y²=0 ==> (x+3-y)(x+3+y)=0 ==.>y=x+3 (ε1) ή y=-x-3 (ε2) ==> λ1=1 και λ2=-1
β) Αρα κάθετες
γ) Τα διανύσματα πρέπει να έχουν αντίστοιχα την ίδια κλίση με τις ευθείες κ/3=λ1 =1 ==> κ=3 και 4λ/(-16)=λ2=-1 ==> λ=4 (αν τις πάρω -1 και 1 βρίσκω αρνητικά κ, λ που απορρίπτονται από την υπόθεση) Άρα Μ(3,4)
δ) y²=2ρχ και επειδή διέρχεται από το Μ(3,4) έχω 4²=2ρ.3 ==> 2ρ=16/3 και
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
bond_bill
Νεοφερμένο μέλος


να αποδειξετε f'(X)>= λ -1 για καθε χ ανηκει στο R
ξερεται πως λυνεται αυτο ?
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Mercury
Επιφανές μέλος


Ξεκινάμε...
Μαθηματικά του Μπάρλα,τεύχος πρώτο,
Σελίδα 65 ασκηση 56:
Έστω
Να δείξετε ότι λ=1
Σελιδα 65 άσκηση 59.
Έστω έ η ευθεία που ορίζουν οι εικόνες των μιγαδικών
Να βρείτε το μιγαδικό w που η εικόνα του βρίσκεται στην ευθεία και έχει το μικρότερο δυνατό μέτρο.
Εδώ βρίσκω τους μιγαδικούς,καταφέρνω να βρώ να την εξίσωση ευθείας,αλλά μετά κολλάω...
Σελίδα 66 ασκηση 63
Έστω
i)Να βρείτε το γεωμετρικό τόπο των σημειων Μ(z) για τα οποία ισχύει η παραπάνω σχέση.(αυτό το έλυσα)
ii)Να βρείτε το γεωμετρικό τόπο των σημείων Ν(w) για τα οποία ισχύει wz=1 (εδώ πρέπει να έχει να κάνει με αντίστροφο του z σωστα; )
Σελιδα 66 ασκηση 66
Αν η εικόνα του μιγαδικού z ανήκει στον κύκλο κέντρου Κ(0,2) και ακτίνας ρ=1 να βρείτε που ανήκει η εικόνα του
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος


Σελιδα 66 ασκηση 66
Αν η εικόνα του μιγαδικού z ανήκει στον κύκλο κέντρου Κ(0,2) και ακτίνας ρ=1 να βρείτε που ανήκει η εικόνα του
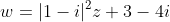
Ο κύκλος C κέντρου Κ(0,2) και ακτίνας ρ=1 έχει εξίσωση στο σύστημα αναφοράς Oxy:
(x^2)+[(y-2)^2]=1
Οι παραμετρικές εξισώσεις του κύκλου C είναι:
x=συνθ
y=2+ημθ
0<=θ<2π
Επομένως για τον μιγαδικό w=x+yi του οποίου η εικόνα Μ(w) ανήκει στον C ισχύει
x=συνθ
y=2+ημθ
Επομένως z=x+yi=συνθ+(2+ημθ)i
Επειδή |1-i|=SQRT((1^2)+((-1)^2))=SQRT(1+1)=SQRT(2) τότε έχουμε
w=2z+3-4i=2(x+yi)+3-4i=2x+2yi+3-4i=(2x+3)+2(y-2)i=(2συνθ+3)+(2ημθ)i
Αν θέσουμε w=X+Yi όπου X,Y ανήκουν R τότε έχουμε:
X=2x+3=2συνθ+3
Y=2(y-2)=2ημθ
Συνεπώς προκύπτει:
((X-3)^2)+(Y^2)=((2συνθ)^2)+((2ημθ)^2)=4[((ημθ)^2)+((συνθ)^2)]=4*1=4
Άρα
[(X-3)^2]+(Y^2)=4
Επομένως η εικόνα M(w) του w ανήκει σε κύκλο C΄ στο σύστημα αναφοράς Oxy με κέντρο Κ΄(3,0) και ακτίνα ρ΄=2
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Mercury
Επιφανές μέλος


Ο κύκλος C κέντρου Κ(0,2) και ακτίνας ρ=1 έχει εξίσωση στο σύστημα αναφοράς Oxy:
(x^2)+[(y-2)^2]=1
Οι παραμετρικές εξισώσεις του κύκλου C είναι:
x=συνθ
y=2+ημθ
0<=θ<2π
Επομένως για τον μιγαδικό w=x+yi του οποίου η εικόνα Μ(w) ανήκει στον C ισχύει
x=συνθ
y=2+ημθ
Επομένως z=x+yi=συνθ+(2+ημθ)i
Επειδή |1-i|=SQRT((1^2)+((-1)^2))=SQRT(1+1)=SQRT(2) τότε έχουμε
w=2z+3-4i=2(x+yi)+3-4i=2x+2yi+3-4i=(2x+3)+2(y-2)i=(2συνθ+3)+(2ημθ)i
Αν θέσουμε w=X+Yi όπου X,Y ανήκουν R τότε έχουμε:
X=2x+3=2συνθ+3
Y=2(y-2)=2ημθ
Συνεπώς προκύπτει:
((X-3)^2)+(Y^2)=((2συνθ)^2)+((2ημθ)^2)=4[((ημθ)^2)+((συνθ)^2)]=4*1=4
Άρα
[(X-3)^2]+(Y^2)=4
Επομένως η εικόνα M(w) του w ανήκει σε κύκλο C΄ στο σύστημα αναφοράς Oxy με κέντρο Κ΄(3,0) και ακτίνα ρ΄=2
Ευχαριστώ!!
Πάντως βγαίνει και πιό απλά χωρίς τριγωνομετρικούς αριθμούς:
Αντικαθιστούμε τα x,y που βρήκαμε στην αρχική εξίσωση κύκλου που μας δίνεται:
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
t00nS
Εκκολαπτόμενο μέλος


1)Να δείξετε ότι:
f(x)<xlnx,για κάθε χε(0,1),f(x)>xlnx για κάθε χ>1 και μετά να λύσετε την εξίσωση f(x)=0
2)να βρείτε τα όρια lim(x->+oo)f(x),lim(x->+oo) f(x)-λ-χ/χ
3)να δείξετε ότι υπάρχει ξε(1,2)τέτοιο ώστε f(τόνος)(ξ)>ln2
βρήκα το πρώτο αλλά δεν είμαι σίγουρος
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Sansy16
Νεοφερμένο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Αν λοιπόν είναι
δηλαδή
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Sansy16
Νεοφερμένο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 5 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 227 μέλη διάβασαν αυτό το θέμα:
- hristosdab
- trifasikodiavasma
- haji
- thepigod762
- Mariosm.
- soulatso
- oteletampis
- phleidhs
- Hased Babis
- AggelikiGr
- sir ImPeCaBlE
- veiNqh
- Scandal
- alekos
- Debugging_Demon
- just some guy
- xristosgkm
- ismember
- Apocalypse
- arrow25
- rempelos42
- ggl
- GStef
- QWERTY23
- xrisamikol
- Σωτηρία
- nikoletaz57
- _Aggelos123
- Mariam38
- SlimShady
- strsismos88
- Georgekk
- Lia 2006
- igeorgeoikonomo
- marian
- tsiobieman
- constansn
- Xristosdimitra
- Panagiotis849
- ρενακι 13
- Memetchi
- eukleidhs1821
- Nikkkpat
- Unboxholics
- korlef
- kwstaseL
- Thanos_D
- the purge
- T C
- Giii
- Papachrist
- liaiscool
- Αννα Τσιτα
- globglogabgalab
- Pharmacist01
- thanahss
- abcdefg12345
- nicole1982
- thecrazycretan
- kvstas92
- KingOfPop
- maria301
- papa2g
- stefan
- Κλημεντίνη
- TonyMontanaEse
- Athens2002
- Alexecon1991
- Μάρκος Βασίλης
- Cortes
- το κοριτσι του μαη
- calliope
- ale
- panagiotis G
- Kleanth
- aggelosst9
- BioChemical
- spring day
- nucomer
- Georgia110
- LeoDel
- pink_panther
- Alexandros973
- marsenis
- den antexw allh apotyxia
- KaterinaL
- kiyoshi
- drosos
- Λαμπρινηη
- Bill22
- Chrysablac.
- giorgosp97
- Βλα
- Monster Hunter
- jul25
- xxxtolis
- Stroka
- nicks1999
- totiloz
- Earendil
- mitsakos
- tasost
- lnesb
- ssalex
- Vasilina93
- alan09
- Livaja10
- χημεια4λαιφ
- Viedo
- UncleJ
- Kostakis45
- Infrared
- Zgian
- pepatogourounaki
- hirasawayui
- GeoCommand
- Eleni54
- American Economist
- EiriniS20
- ΘανάσοςG4
- stamoul1s
- Αριάνα123
- uni77
- Libertus
- tasoss
- PanosCh002
- Unseen skygge
- Νικόλας Ραπ.
- cel123
- The Limit Does Not Exist
- don_vito
- suaimhneas
- Αλκης Κ.
- alexrami
- Baggelitsa36
- Νομικάριος13
- spinalgr1990
- d_th
- Adolfo valencia
- Πα.Κ
- Vasilis25
- Johnman97
- Steffie88
- rekcoR
- gwgw_5
- fockos
- Mariahj
- roud
- kostas83
- Cpt.Philips
- Makis45
- Χρησλου
- Panos_02
- Vold
- tymvorixos
- GiorgosAsi
- Neos167
- theodoraooo
- George187
- Άρτεμις Α.
- Μαρία2222
- christos87
- Idontknoww
- jimis2001
- Metamorph
- Γατόπαρδος.
- Johnsk
- mitsos14
- johnsiak
- Elel
- Dreamer_SW
- Γιαννης1987Θεσσ
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki

