Βοήθεια/Aπορίες στα Μαθηματικά Προσανατολισμού

[Mercury]

Όπου z θα βαλεις το f(z).

Και τον z συζυγή δεν τον πειράζω καθόλου;

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[antwwwnis]

Θα γραφει (f(z))συζυγης

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Civilara]

Απορία:

Να δείξετε ότι

Θέτουμε z=x+yi όπου x=Re(z) και y=Im(z). Ο συζυγής του z είναι z_=x-yi. Έχουμε:

f(z)=[(3+4i)/6](x+yi)+(5/6)(x-yi)=...=[(4x-2y)/3]+[(2x-y)/3]i=[(4Re(z)-2Im(z))/3]+[(2Re(z)-Im(z))/3]i

Άρα

Re(f(z))=(4x-2y)/3=(4Re(z)-2Im(z))/3
Im(f(z))=(2x-y)/3=(2Re(z)-Im(z))/3

Έχουμε f(f(z))=Re(f(f(z))+Im(f(f(z))i όπου

Re(f(f(z)))=[4Re(f(z))-2Im(f(z))]/3=(1/3){4[(4x-2y)/3]-2[(2x-y)/3]}=(4x-2y)/3=Re(f(z))
Im(f(f(z)))=[2Re(f(z))-Im(f(z))]/3=(1/3){2[(4x-2y)/3]-[(2x-y)/3]}=(2x-y)/3=Im(f(z))

Επειδή Re(f(f(z)))=Re(f(z)) και Im(f(f(z))=Im(z) για οποιονδήποτε z ανήκει C τότε f(f(z))=f(z)

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[aris-bas]

1)ενα κινητο κινειται στο μιγαδικο επιπεδο με τετοιο τροπο ,ωστε τη χρονικη στιγμη t να βρισκεται στο σημειο που ειναι εικονα του μιγαδικοu z=3συνt-(3ημt-2)i
α)να αποδειξετε οτι το κινητο κινειται σε κυκλο με κεντρο την εικονα του μιγαδικου 2i και ακτινα ρ=3
β)να υπολογισετε τη μικροτερη αποσταση του κινητου απο την αρχη των αξονων.

2)δινεται η συναρτηση f(z)= [iz-2+4i] / [z-i] με z διαφορο του i.Eστω επισης u=z-1 ,w=f(z)-i
α)να αποδειξετε οτι uw=-3+4i
β)να βρεθει ο z οταν u=w
γ)να λυθει η εξισωση f(z)=1-i
δ)να βρεθει ο γ.τ. των εικονων του z,οταν f(z) ε R.

Kαμια βοηθεια κανεις?

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Civilara]

1)ενα κινητο κινειται στο μιγαδικο επιπεδο με τετοιο τροπο ,ωστε τη χρονικη στιγμη t να βρισκεται στο σημειο που ειναι εικονα του μιγαδικοu z=3συνt-(3ημt-2)i
α)να αποδειξετε οτι το κινητο κινειται σε κυκλο με κεντρο την εικονα του μιγαδικου 2i και ακτινα ρ=3
β)να υπολογισετε τη μικροτερη αποσταση του κινητου απο την αρχη των αξονων.

α) Είναι z=x+yi όπου x=συνt και y=-(3ημt-2)=2-3ημt όπου t ανήκει R. Έχουμε:

|z-2i|=|3συνt-(3ημt-2)i-2i|=|3συνt-(3ημt)i|=SQRT[((3συνt)^2)+((-3ημt)^2)]=3SQRT[((συνt)^2)+((ημt)^2)]=3*SQRT(1)=3*1=3

Άρα |z-z0|=ρ όπου z0=2i και ρ=3 που σημαίνει ότι το Μ(z) ανήκει σε κύκλο κέντρο K(2i)=K(0,2) και ακτίνα ρ=3

β) Η απόσταση (ΟΜ) ισούται με:

(ΟΜ)=|z|=|3συνt-(3ημt-2)i|=|3συνt+(2-3ημt)i|=SQRT[((3συνt)^2)+((2-3ημt)^2)]=SQRT[9((συνt)^2)+4-12ημt+9((ημt)^2)]
(ΟΜ)=SQRT[9(((ημt)^2)+((συνt)^2))+4-12ημt]=SQRT(9+4-12ημt)=SQRT(13-12ημt)=f(t)

Άρα f(t)=SQRT(13-12ημt), t ανήκει R

Για κάθε t ανήκει R έχουμε:

-1<=ημt<=1 <=> -12<=-12ημt<=12 <=> 1<=13-12ημt<=25 <=> 1<=SQRT(13-12ημt)<=5 <=> 1<=f(t)<=5

Άρα minf(t)=1

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[vimaproto]

1)ενα κινητο κινειται στο μιγαδικο επιπεδο με τετοιο τροπο ,ωστε τη χρονικη στιγμη t να βρισκεται στο σημειο που ειναι εικονα του μιγαδικοu z=3συνt-(3ημt-2)i
α)να αποδειξετε οτι το κινητο κινειται σε κυκλο με κεντρο την εικονα του μιγαδικου 2i και ακτινα ρ=3
β)να υπολογισετε τη μικροτερη αποσταση του κινητου απο την αρχη των αξονων.

2)δινεται η συναρτηση f(z)= [iz-2+4i] / [z-i] με z διαφορο του i.Eστω επισης u=z-1 ,w=f(z)-i
α)να αποδειξετε οτι uw=-3+4i
β)να βρεθει ο z οταν u=w
γ)να λυθει η εξισωση f(z)=1-i
δ)να βρεθει ο γ.τ. των εικονων του z,οταν f(z) ε R.

Kαμια βοηθεια κανεις?

1) Ζ=3συνt +(2-3ημt)i ==> x=3συνt, y=2-3ημt ή 2-y=3ημt υψώνω στο τετράγωνο τις δύο σχέσεις και χ²+(2-y)²=3²(ημ²t +συν²t)=3² ή χ²+(y-2)=3² η οποία δηλώνει ότι το κέντρο είναι Κ(0,2) και η ακτίνα ρ=3 Δηλ. εικόνα του μιγαδικού 0+2i
β) Εστο Μ σημείο του κύκλου. Τότε τριγωνική ανισότητα ΚΜ-ΟΚ<=ΟΜ<=ΚΜ+ΟΚ ==> 3-2<=ΟΜ<=3+2 ==> 1<=ΟΜ<=5 (ΚΜ=ακτίνα)
Αρα η ελάχιστη τιμή ΟΜ=1

2) Εδώ πρέπει να διορθώσεις u=z-i
Βρες την w και πολλαπλασίασε την με την u
Τα άλλα είναι εύκολα βάζοντας z=x+yi

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[mary-blackrose]

καλησπερα θα ηθελα τη βοηθεια σας στις παρακατω ασκησεις:
1)δινεται η συναρτηση f(x)={
{0 , x=0
α) να δειξετε οτι η f ειναι συνεχης
β)να μελετησετε την f ως προς τη μονοτονια,τα ακροτατα,τα κοιλα και να βρειτε τα σημεια καμπης της Cf.
γ)να βρειτε το συνολο τιμων της f και το πληθος των ριζων της εξισωσης

2)εστω f μια συναρτηση δυο φορες παραγωγισιμη στο R με ,,για καθε ,f'(1)>0 και η συναρτηση
α) να βρεθουν οι ριζες και το προσημο της Cg.
β)να βρεθουν τα διαστηματα που η g ειναι κυρτη ή κοιλη και τα σημεια καμπης της Cg.

υ.γ. η f(x) στη 1η ασκηση ειναι δικλαδη με κλαδους (πανω) και (κατω) 0 , χ=0

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[vivianouz]

δινεται η συναρτηση
α) να βρειτε τα ωστε το Α(1,3) να ειναι σημειο καμπης της Cf
β)για α=4 και β=-1
ι)να βρεθουν τα διαστηματα που η Cf ειναι κυρτη ή κοιλη
ιι)να βρεθει η εφαπτομενη της Cf στο σημειο καμπης της
ιιι)να δειχθει οτι
καμια βοηθεια κανεις στην παραπανω???

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Civilara]

2)εστω f μια συναρτηση δυο φορες παραγωγισιμη στο R με ,,για καθε ,f'(1)>0 και η συναρτηση
α) να βρεθουν οι ριζες και το προσημο της Cg.
β)να βρεθουν τα διαστηματα που η g ειναι κυρτη ή κοιλη και τα σημεια καμπης της Cg.

α) Επειδή η f είναι δύο φορές παραγωγίσιμη στο R τότε η f΄ είναι παραγωγίσιμη στο R οπότε και συνεχής στο R. Επιεδή η f΄ είναι συνεχής στο R και ισχύει f΄(x) διάφορο 0 για κάθε x ανήκει R τότε η f΄ διατηρεί σταθερό πρόσημο στο R. Επειδή η f΄ διατηρεί σταθερό πρόσημο στο R και f΄(1)>0 τότε f΄(x)>0 για κάθε x ανήκει R. Η f είναι παραγωγίσιμη στο R οπότε είναι και συνεχής στο R.

Η f είναι συνεχής και παραγωγίσιμη στο R και ισχύει f΄(x)>0 για κάθε x ανήκει R. Άρα η f είναι γνησίως αύξουσα στο R.

Επειδή η f είναι παραγωγίσιμη στο R τότε και η g είναι παραγωγίσιμη στο R, οπότε και συνεχής στο R, με πρώτη παράγωγο:
g΄(x)=f΄(x)+f΄(2-x), x ανήκει R

Επειδή f΄(x)>0 για κάθε x ανήκει R τότε f΄(2-x)>0 για κάθε x ανήκει R. Προσθέτοντας κατά μέλη τις δύο τελευταίες ανισότητες προκύπτει:
f΄(x)+f΄(2-x)>0 => g΄(x)>0 για κάθε x ανήκει R

Η g είναι συνεχής και παραγωγίσιμη στο R και ισχύει g΄(x)>0 για κάθε x ανήκει R. Άρα η g είναι γνησίως αύξουσα στο R. Έχουμε:

g(1)=f(1)-f(2-1)=f(1)-f(1)=0

x<1 <=> g(x)<g(1) <=> g(x)<0
x>1 <=> g(x)>g(1) <=> g(x)>0

Άρα g(x)<0 για κάθε x ανήκει (-οο,1), g(x)>0 για κάθε x ανήκει (1,+οο) και g(1)=0

β) Επειδή η f είναι 2 φορές παραγωγίσιμη στο R τότε και η g είναι δύο φορές παραγωγίσιμη στο R με δεύτερη παράγωγο:
g΄΄(x)=f΄΄(x)-f΄΄(2-x), x ανήκει R

Γνωρίζουμε ότι η f΄΄ είναι γνησίως φθίνουσα στο R. Έχουμε:

g΄΄(1)=f΄΄(1)-f΄΄(2-1)=f΄΄(1)-f΄΄(1)=0

x<1 <=> 2x<2 <=> x+x<2 <=> x<2-x <=> f΄΄(x)>f΄΄(2-x) <=> f΄΄(x)-f΄΄(2-x)>0 <=> g΄΄(x)>0
x>1 <=> 2x>2 <=> x+x>2 <=> x>2-x <=> f΄΄(x)<f΄΄(2-x) <=> f΄΄(x)-f΄΄(2-x)<0 <=> g΄΄(x)<0

Η g είναι συνεχής στο (-οο,1], δύο φορές παραγωγίσιμη στο (-οο,1) και ισχύει g΄΄(x)>0 για κάθε x ανήκει (-οο,1). Άρα η g είναι κυρτή στο (-οο,1). Η g είναι συνεχής στο [1,+οο), δύο φορές παραγωγίσιμη στο (1,+οο) και ισχύει g΄΄(x)<0 για κάθε x ανήκει (1,+οο). Άρα η g είναι κοίλη στο [1,+οο).

Η g είναι συνεχής στο R, κυρτή στο (-οο,1] και κοίλη στο [1,+οο). Επομένως το σημείο M(1,g(1)) είναι σημείο καμπής της Cg.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[greekgohan]

δινεται η συναρτηση
α) να βρειτε τα ωστε το Α(1,3) να ειναι σημειο καμπης της Cf
β)για α=4 και β=-1
ι)να βρεθουν τα διαστηματα που η Cf ειναι κυρτη ή κοιλη
ιι)να βρεθει η εφαπτομενη της Cf στο σημειο καμπης της
ιιι)να δειχθει οτι
καμια βοηθεια κανεις στην παραπανω???

Eχεις 2 σχεσεις οπου μπορεις να βρεις α και β. f(1)=3 και f''(1)=0.
ι)Μετα με f''(x)=0 και με πινακακι βρισκεις διαστηματα
ii)παιρνεις τον τυπο ψ-f(1)=f'(1)(x-1) και την βρισκεις
ιιι)εφοσον f(1) ειναι μεγιστο θα ισχυει:f(x)<=f(1)

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Civilara]

καλησπερα θα ηθελα τη βοηθεια σας στις παρακατω ασκησεις:
1)δινεται η συναρτηση f(x)={
{0 , x=0
α) να δειξετε οτι η f ειναι συνεχης
β)να μελετησετε την f ως προς τη μονοτονια,τα ακροτατα,τα κοιλα και να βρειτε τα σημεια καμπης της Cf.
γ)να βρειτε το συνολο τιμων της f και το πληθος των ριζων της εξισωσης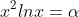

α) Θεωρούμε τις συναρτήσεις g(x)=1/x, Dg=R* και h(x)=lnx, Dh=(0,+oo).

Η g είναι συνεχής και παραγωγίσιμη στο R* με πρώτη παράγωγο g΄(x)=-1/(x^2).
Είναι lim(x->0+)g(x)=lim(x->0+)(1/x)=+oo

Η h είναι συνεχής και παραγωγίσιμη στο (0,+oo) με πρώτη παράγωγο h΄(x)=1/x.
Είναι lim(x->0+)h(x)=lim(x->0+)lnx=-oo

Έχουμε
lim(x->0+)[h΄(x)/g΄(x)]=lim(x->0+)[(1/x)/(-1/(x^2))]=lim(x->0+)[-(x^2)/x]=lim(x->0+)(-x)=-0=0

Επειδή lim(x->0+)h(x)=-oo και lim(x->0+)g(x)=+oo τότε σύμφωνα με τον 2ο κανόνα De L' Hospital έχουμε:
lim(x->0+)[h(x)/g(x)]=lim(x->0+)[h΄(x)/g΄(x)]=0

Άρα
lim(x->0+)(xlnx)=lim(x->0+)[lnx/(1/x)]=lim(x->0+)[h(x)/g(x)]=0
lim(x->0+)f(x)=lim(x->0+)[(x^2)lnx]=[lim(x->0+)x]*[lim(x->0+)(xlnx)]=0*0=0=f(0)

Επειδή lim(x->0+)f(x)=f(0) τότε η f είναι συνεχής στο x0=0. Για x>0 είναι f(x)=(x^2)lnx, οπότε η f είναι συνεχής στο (0,+οο) ως γινόμενο συνεχών συνρτήσεων. Άρα η f είναι συνεχής στο [0,+οο).

β) Η f είναι παραγωγίσιμη στο (0,+οο) με πρώτη παράγωγο:
f΄(x)=2xlnx+x=(2lnx+1)x, x>0

lim(x->0+)[(f(x)-f(0))/(x-0)]=lim(x->0+)[((x^2)lnx)/x]=lim(x->0+)(xlnx)=0
Άρα η f είναι παραγωγίσιμη στο x0=0 με πρώτη παράγωγο f΄(0)=0. Συνεπώς η f είναι παραγωγίσιμη στο [0,+οο).

f΄(0)=f΄(1/SQRT(e))=0

Η f είναι συνεχής στο [0,1/SQRT(e)], παραγωγίσιμη στο (0,1/SQRT(e)) και ισχύει f΄(x)<0 για κάθε x ανήκει (0,1/SQRT(e)). Άρα η f είναι γνησίως φθίνουσα στο [0,1/SQRT(e)].
Η f είναι συνεχής στο [1/SQRT(e),+οο), παραγωγίσιμη στο (1/SQRT(e),+οο) και ισχύει f΄(x)>0 για κάθε x ανήκει (1/SQRT(e),+οο). Άρα η f είναι γνησίως αύξουσα στο [1/SQRT(e),+οο).

Η f είναι συνεχής στο [0,+οο), γνησίως φθίνουσα στο [0,1/SQRT(e)] και γνησίως αύξουσα στο [1/SQRT(e),+οο). Επομένως η f παρουσιάζει ολικό ελάχιστο στο x0΄=1/SQRT(e) με τιμή f(1/SQRT(e))=-1/(2e)

H f΄ είναι παραγωγίσιμη στο (0,+οο), οπότε η f είναι δύο φορές παραγωγίσιμη στο (0,+οο) με δεύτερη παράγωγο
f΄΄(x)=2lnx+3, x>0

lim(x->0+)[((f΄(x)-f΄(0))/(x-0)]=lim(x->0+)(2lnx+1)=-oo εφόσον lim(x->0+)lnx=-oo
Άρα η f δεν είναι δύο φορές παραγωγίσιμη στο x0=0.

Έχουμε f΄΄(1/(eSQRT(e)))=0

Η f είναι συνεχής στο [0,1/(eSQRT(e))], δύο φορές παραγωγίσιμη στο (0,1/(eSQRT(e))) και ισχύει f΄΄(x)<0 για κάθε x ανήκει (0,1/(eSQRT(e))). Άρα η f είναι κοίλη στο [0,1/(eSQRT(e))].
Η f είναι συνεχής στο [1/(eSQRT(e)),+οο), παραγωγίσιμη στο (1/(eSQRT(e)),+οο) και ισχύει f΄΄(x)>0 για κάθε x ανήκει (1/(eSQRT(e)),+οο). Άρα η f είναι κυρτή στο [1/(eSQRT(e)),+οο).

Το σημείο Α(1/(eSQRT(e)),f(1/(eSQRT(e)))) είναι σημείο καμπής της Cf. Έχουμε f(1/(eSQRT(e)))=-3/(2(e^3))

γ) Επειδή lim(x->+oo)(x^2)=lim(x->+oo)lnx=+oo τότε lim(x->+oo)f(x)=lim(x->+oo)[(x^2)lnx]=+oo.

Η f είναι συνεχής και γνησίως φθίνουσα στο [0,1/SQRT(e)]. Επομένως
f([0,1/SQRT(e)])=[f(1/SQRT(e)),f(0)]=[-1/(2e),0]

Η f είναι συνεχής και γνησίως αύξουσα στο [1/SQRT(e),+οο). Επομένως
f([1/SQRT(e),+οο))=[f(1/SQRT(e)),lim(x->+oo)f(x))=[-1/(2e),+oo)

Στη συνέχεια θα προσδιοριστεί το πλήθος των πραγματικών ριζών της εξίσωσης f(x)=α όπου α ανήκει R.

Αν α<-1/(2e) τότε η εξίσωση f(x)=α είναι αδύνατη αφού f(x)>=-1/(2e) για κάθε x ανήκει [0,+οο)
Αν α=-1/(2e) τότε η εξίσωση f(x)=α έχει μοναδική λύση την x=1/SQRT(e) που είναι και η θέση του ελαχίστου
Αν -1/(2e)<α<=0 τότε η εξίσωση f(x)=α έχει δύο ρίζες, την x1 ανήκει [0,1/SQRT(e)) και την x2 ανήκει (1/SQRT(e),1]
Αν α>0 τότε η εξίσωση f(x)=α έχει μοναδική λύση στο διάστημα (1,+οο) (καθώς για x>1 έχουμε f(x)>f(1) => f(x)>0 λόγω της μονοτονίας της f)

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[paokara123]

παιδια οποιος μπορει να λυσει το οριο lim(x->0) x*e^(1/x)

Σημείωση συντονιστή : Τα μηνύματα 6548,6350 προήλθαν από νήμα με παρόμοιο θέμα.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[g1wrg0s]

Για θεσε 1/x = u , γραψε καλα το οριο και κανε και ενα DLH .

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[rebel]

Δεν υπάρχει.

ενώ

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Mercury]

i)Να δείξετε ότι αυτό το έλυσα
ii)Άν να βρεθεί το
Εδώ έχω κολλήσει,οπότε θα ήθελα λίγο insight/hints για το πώς να ξεκινήσω την επίλυση

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Solmyr]

i)Να δείξετε ότι αυτό το έλυσα
ii)Άν να βρεθεί το
Εδώ έχω κολλήσει,οπότε θα ήθελα λίγο insight/hints για το πώς να ξεκινήσω την επίλυση

νομίζω βγαίνει 1(γρήγορα το έκανα.Δεν είμαι σίγουρος).Επειδή δε ξέρω πως να το γράψω θα σου εξηγήσω.

στον παρανομαστη το |z|^2 ισουται με 1(το εχεις αποδειξει στο προηγουμενο ερωτημα).Υστερα κοινο παραγοντα το z^3 στον αριθμητη και ιδιοτητα στο μετρο στον παρανομαστη.Γινεται απλοποιηση και σου μενει |z^3| το οποιο ειναι ισο με μοναδα.Καπως ετσι...

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Mercury]

Για να καταλάβω,γίνεται έτσι:

Μετά το γράφω σαν μέτρο και;
Σορρυ,αλλά με έχει παιδέψει πολύ η συγκεκριμένη..

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Solmyr]

Για να καταλάβω,γίνεται έτσι:

Μετά το γράφω σαν μέτρο και;
Σορρυ,αλλά με έχει παιδέψει πολύ η συγκεκριμένη..

το γραφεις σαν μετρο.

το μετρο παει και στον αριθμητη και στον παρανομαστη

λογω μιας ιδιοτητας ο παρανομαστης γινεται z + i

βγαζεις κοινο παραγοντα το z^3 στον αριθμητη

γινεται απλοποιηση του αριθμητη με τον παρανομαστη

μενει |w|=|z^3|=|z|^3=1

Ζητώ συγγνώμη για τον τρόπο που το έγραψα,αλλά όπως είπα και πριν δε ξέρω πως να χρησιμοποιώ τα μαθηματικά σύμβολα.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Mercury]

Λές για αυτήν την ιδιότητα;

Νόμιζα ισχύει μόνο όταν έχεις σκέτο συζυγή στο μέτρο..
Θένκς!!

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Mercury]

Βασικά άκυρο το παραπάνω..
Πρέπει να λές αυτή:
Οπότε η εξίσωση γίνεται:


Σωστα;

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.