aris-bas
Νεοφερμένο μέλος



Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος


Καμια ιδεα για την παρακατω....
εστω συναρτηση f συνεχης στο R ωστε να ισχυει :
f(x)+f(x+5)=0 για καθε χ ε R
Να αποδειξετε οτι:
α)η συναρτηση f ειναι περιοδικη
β)υπαρχουν απειροι αριθμοι θ ε R ωστε f(θ)=f(θ+5)
α) f(x)+f(x+5)=0 <=> f(x+5)=-f(x) για κάθε x ανήκει R
Άρα f((x+5)+5)=-f(x+5) => f(x+10)=-f(x+5) => f(x+10)=-(-f(x)) => f(x+10)=f(x) για κάθε x ανήκει R
Επομένως f((x-10)+10)=f(x-10) => f(x)=f(x-10)
Άρα ισχύει f(x+10)=f(x-10)=f(x) για κάθε x ανήκει R
Θα δειχθεί στη συνέχεια με τη μέθοδο της μαθηματικής επαγωγής ότι για κάθε n ανήκει Ν* ισχύει f(x+10n)=f(x) για κάθε n ανήκει R.
Για n=1 η σχέση γίνεται f(x+10)=f(x) που ισχύει
Αν ισχύει f(x+10n)=f(x) τότε θα δειχθεί ότι f(x+10(n+1))=f(x). Έχουμε
f(x+10(n+1))=f(x+10n+10)=f((x+10n)+10)=f(x+10n)=f(x)
Άρα ισχύει f(x+10n)=f(x) για κάθε n ανήκει N*
Με τον ίδιο τρόπο μπορεί να δειχθεί ότι ισχύει f(x-10n)=f(x) για κάθε n ανήκει Ν*
Επομένως ισχύει f(x+10n)=f(x) για κάθε n ανήκει Z*. Άρα η f είναι περιοδική με περίοδο Τ=10.
β) Αν υπάρχει x0 ανήκει R με f(x0)=0 τότε f(x0+5)=-f(x0)=-0=0, οπότε f(x0+5)=f(x0)=0 και επειδή η f είναι περιοδική με περίοδο T=10 τότε ισχύει f(x0+10n)=f(x0)=0=f(x0+5) για κάθε n ανήκει Z*. Άρα τα x για τα οποία x=x0+10n, όπου n ανήκει Z είναι λύσεις της εξίσωσης f(x)=f(x+5).
Αν f(x0) διάφορο 0 τότε f(x0+5)=-f(x0) => f(x0)f(x0+5)=-(f(x0)^2)<0. Επειδή η f είναι συνεχής στο [x0,x0+5] και ισχύει f(x0)f(x0+5)<0 τότε σύμφωνα με το θεώρημα Bolzano υπάρχει τουλάχιστον ένα ξ ανήκει (x0,x0+5) τέτοιο ώστε f(ξ)=0. Ακολουθώντας την προηγούμενη ανάλυση, όλα τα x για τα οποία x=ξ+10n, όπου n ανήκει Z είναι λύσεις της εξίσωσης f(x)=f(x+5).
Επομένως υπάρχουν άπειροι πραγματικοί αριθμοί θ τέτοιοι ώστε f(θ)=f(θ+5).
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
vimaproto
Πολύ δραστήριο μέλος


1) Η εφαπτομένη έχει τη μορφή y=λx+k. λ=f'(a)δινεται ησυναρτηση f(x)=xlnx
ι)να βρειτε την εξισωση της εφαπτομενης της cf σε σημειο Α(α,f(α)), α>ο
ιι)αν η τετμημενη α αυξανει με ρυθμο 2cm/sec να βρειτε το ρυθμο μεταβολης τουεμβαδου που σχηματιζει η εφαπτομενη cf με τους αξονες α=5cm
f'(x)=lnx+1 ==> λ=f'(a)=lna+1=lnae. To k το προσδιορίζω από τις συντεταγμένες του Α και f(a)=a.lnae+k ==>alna=alnae+k ==> k= -a
Αρα η εφαπτομένη είναι y=xlnae - a
2) Δεν μπορώ να κάνω σχήμα γιαυτό θα σου περιγράψω τη λύση.
Η εφαπτομένη τέμνει τους άξονες τον μεν y στο σημείο y1= -α και τον χ στο σημείο χ1=α/lnαe
Tο τρίγωνο που σχηματίζεται έχει εμβαδόν Ε=½x1*y1=½.a²/lnae που το παραγωγίζω ως προς τον χρόνο και με δοσμένο ότι dα/dt=2 και α=5 καθώς και ln5=1,6 βρίσκω dE/dt=3,1
Τώρα βλέπω ότι έκανα τόσο κόπο και με πρόλαβε άλλος
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος


3)εστω f(x)=x-ln(1+(e^x)) , x ε R
α)να δειξετε οτι f(1)=1+f(-1)
β)να αποδειξετε οτι υπαρχει τουλαχιστον ενα χο ε (-1,1) τετοιο ωστε 2f'(xo)=1
γ)να βρεθει η εφαπτομενη της Cf // x-2y+1=0
δ)να μελετησετε την f ως προς τη μονοτονια
ε)να βρειτε τη θεση της Cf ως προς την εφαπτομενη του (γ) ερωτηματος
ζ)να αποδειξετε οτι lim f(x)=-00
x->-00
η)να βρειτε το lim f(x)
x->+00
θ)να δειξετε οτι η y=x ειναι ασυμπτωτη της Cf.
α) f(x)=x-ln(1+(e^x))=ln(e^x)-ln(1+(e^x))=ln[(e^x)/(1+(e^x))]=ln[1/((e^(-x))+1)]=ln{[((e^(-x))+1]^(-1)}=-ln[((e^(-x))+1], x ανήκει R
f(1)=1-ln(1+(e^1))=1-ln(1+e)=1-ln(1+e)
f(-1)=-ln[((e^(-(-1)))+1]=-ln[(e^1)+1]=-ln(1+e)
Επομένως f(1)=1+f(-1) <=> f(1)-f(-1)=1
β) Η f είναι συνεχής και παραγωγίσιμη στο R με πρώτη παράγωγο:
f΄(x)=(-ln[((e^(-x))+1])΄=1/((e^x)+1)
Η f είναι συνεχής στο [-1,1] και παραγωγίσιμη στο (-1,1). Επομένως σύμφωνα με το θεώρημα μέσης τιμής υπάρχει τουλάχιστον ένα x0 ανήκει (-1,1) τέτοιο ώστε f΄(x0)=(f(1)-f(-1))/(1-(-1))=1/2 <=> 2f΄(x0)=1
γ) (ε): x-2y+1=0 <=> 2y=x+1 <=> y=(1/2)x+(1/2)
Η ευθεία ε έχει συντελεστή διεύθυνσης λε=1/2=f΄(x0)
Για να προσδιοριστεί το x0 λύνουμε την εξίσωση f΄(x0)=1/2
f΄(x0)=1/2 <=> 1/((e^x0)+1)=1/2 <=> (e^x0)+1=2 <=> e^x0=1 <=> x=0
Έχουμε f(0)=0-ln(1+(e^0))=-ln(1+1)=-ln2 και f΄(0)=1/2
Η εφαπτομένη (ζ) της Cf στο σημείο (0,f(0)) έχει εξίσωση:
y-f(0)=f΄(0)(x-0) <=> y=f΄(0)x+f(0) <=> y=(1/2)x-ln2
δ) Έχει βρεθεί ότι f΄(x)=1/((e^x)+1)
Η f είναι συνεχής και παραγωγίσιμη στο R και ισχύει f΄(x)>0 για κάθε x ανήκει R. Επομένως η f είναι γνησίως αύξουσα στο R.
ε) Θεωρούμε την συνάρτηση φ(x)=(e^x)-2(e^(x/2))+1, x ανήκει R. Η συνάρτηση φ είναι συνεχής και παραγωγίσιμη στο R με πρώτη παράγωγο φ΄(x)=(e^x)-(e^(x/2))=(e^(x/2))((e^(x/2))-1)
φ΄(x)=0 <=> e^(x/2)=1 <=> x/2=0 <=> x=0
Η συνάρτηση φ είναι συνεχής στο (-οο,0], παραγωγίσιμη στο (-οο,0) και ισχύει φ(x)<0 για κάθε x ανήκει (-οο,0). Άρα η φ είναι γνησίως φθίνουσα στο (-οο,0].Η συνάρτηση φ είναι συνεχής στο [0,+oo), παραγωγίσιμη στο (0,+oo) και ισχύει φ(x)>0 για κάθε x ανήκει (0,+oo). Άρα η φ είναι γνησίως αύξουσα στο [0,+οο). Επομένως η φ παρουσιάζει ολικό ελάχιστο στο 0 με τιμή φ(0)=1-2+1=0.
x<0 => φ(x)>φ(0) => φ(x)>0
x>0 => φ(x)>φ(0) => φ(x)>0
Επομένως για κάθε x ανήκει R* ισχύει φ(x)>0. Για κάθε x ανήκει R* έχουμε:
φ(x)>0 <=> (e^x)-2(e^(x/2))+1>0 <=> 2(e^(x/2))<(e^x)+1 <=> [2(e^(x/2))]/[(e^x)+1]<1 <=> ln{[2(e^(x/2))]/[(e^x)+1]}<0 για κάθε x ανήκει R*
Θεωρούμε την συνάρτηση g της εφαπτομένης της Cf στο (0,f(0)) με τύπο g(x)=(1/2)x-ln2, x ανήκει R.
Θεωρούμε την συνάρτηση h(x)=f(x)-g(x), x ανήκει R. Έχουμε
h(x)=x-ln(1+(e^x))-(x/2)+ln2=(x/2)+ln[2/(1+(e^x))]=ln(e^(x/2))+ln[2/(1+(e^x))]=ln{[2(e^(x/2))]/(1+(e^x))]}
Έχουμε βρει ότι για κάθε x ανήκει R* ισχύει ln{[2(e^(x/2))]/[(e^x)+1]}<0 <=> h(x)<0 <=> f(x)<g(x)
Για x=0 έχουμε f(0)=g(0)=-ln2
ζ) Θεωρούμε τον μετασχηματισμό u=-x. Επειδή lim(x->-oo)(-x)=+oo, έχουμε
lim(x->-oo)(e^(-x))=lim(u->+oo)(e^u)=+oo
Θεωρούμε τον μετασχηματισμό t=(e^(-x)), οπότε
lim(x->-oo)[1+(e^(-x))]=lim(t->+oo)(1+t)=lim(t->+oo)t=+oo
Θεωρούμε τον μετασχηματισμό s=1+(e^(-x))
lim(x->-oo)ln[1+(e^(-x))]=lim(s->+oo)lns=+oo
Επομένως lim(x->-oo)f(x)=lim(x->-oo){-ln[1+(e^(-x))]}=-oo
η)
lim(x->+oo)(-x)=-oo
lim(x->+oo)(e^(-x))=lim(u->-oo)(e^u)=0
lim(x->+oo)f(x)=lim(x->+oo){-ln[1+(e^(-x))]}=-ln(1+0)=-ln1=-0=0
Άρα lim(x->+oo)f(x)=0
θ) Θα υπολογίσουμε το όριο lim(x->-oo)f΄(x). Έχουμε
Επειδή lim(x->-oo)(e^x)=0 τότε lim(x->-oo)f΄(x)=lim(x->-oo)[1/((e^x)+1)]=1/(0+1)=1/1=1
Θεωρούμε την συνάρτηση P(x)=x. Η P είναι συνεχής και παραγωγίσιμη στο R με πρώτη παράγωγο P΄(x)=1 και ισχύει
lim(x->-oo)P(x)=-oo.
Επειδή lim(x->-oo)f(x)=lim(x->-oo)P(x)=-oo, τότε το όριο lim(x->-oo)[f(x)/P(x)] οδηγεί σε απροσδιόριστη μορφή (-oo)/(-oo). Στη συνέχεια υπολογίζουμε το όριο lim(x->-oo)[f΄(x)/P΄(x)]. Έχουμε:
lim(x->-oo)[f΄(x)/P΄(x)]=lim(x->-oo)f΄(x)=1
Επομένως σύμφωνα με τον 2ο κανόνα De L' Hospital είναι lim(x->-oo)[f(x)/P(x)]=lim(x->-oo)[f΄(x)/P΄(x)]=1
Έχουμε
lim(x->-oo)[f(x)/P(x)]=1 => lim(x->-oo)[f(x)/x]=1=λ
Στη συνέχεια θα υπολογιστεί το όριο lim(x->-oo)[f(x)-λx]=lim(x->-oo)[f(x)-x]. Έχουμε:
lim(x->-oo)[f(x)-λx]=lim(x->-oo)[f(x)-x]=lim(x->-oo)[x-ln(1+(e^x))-x]=lim(x->-oo)[-ln(1+(e^x))]=-ln(1+0)=-ln1=-0=0=β
Επομένως η ευθεία (η) y=λx+β <=> y=x είναι ασύμπτωτη της Cf στο -οο.
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Aris90
Εκκολαπτόμενο μέλος


f'(ξ)=a+b-2ξ/(ξ-α)(ξ-β)
και τι πρεπει να πω οταν μου λεει ν.δ.ο οτι εφαρμοζεται το θεωρημα rolle για τη συναρτηση
g(x)=f(x)e^-λx λΕR [a,b]
για την πρωτη ασκηση δεν θελω καποια λυση αλλα καποιο καλο tip ειναι η πρωτη με τετοιο ειδους που κανω
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
P@NT?LO$
Νεοφερμένο μέλος


1
2
Ειναι απο τις ασεκησεις 31ιιι,32ιιι του 2ου βιβλιου του μπαρλα σελιδα 89
δεν μπορω να τις λυσω... βοηθεια και καλη χρονια κιολας!!
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος


Να βρειτε τον τυπο της συναρτησης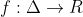
1,
\neq 0)
και
=1)
f΄(x)+2x(f(x)^2)=0 <=> [f΄(x)/(f(x)^2)]+2x=0 για κάθε x ανήκει R
Θεωρούμε την συνάρτηση g(x)=(1/f(x))-(x^2), x ανήκει R. Επειδή η f είναι παραγωγίσιμη στο R τότε και η g είναι παραγωγίσιμη στο R, οπότε και συνεχής στο R, με πρώτη παράγωγο
g΄(x)=-[((f΄(x))/(f(x)^2))+2x]=-0=0
Η g είναι συνεχής και παραγωγίσιμη στο R και ισχύει g΄(x)=0 για κάθε x ανήκει R. Επομένως υπάρχει πραγματική σταθερά c έτσι ώστε να ισχύει g(x)=c για κάθε x ανήκει R. Έχουμε:
g(0)=(1/f(0))-(0^2)=(1/1)-0=1
g(0)=c
Επομένως c=1. Άρα
g(x)=1 <=> (1/f(x))-(x^2)=1 <=> f(x)=1/((x^2)+1), x ανήκει R
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος


Να βρειτε τον τυπο της συναρτησης
2=\frac{1}{{x}^{2}}-\frac{f(x)}{x})
και
=-f(-1)=e)
f΄(x)=(1/(x^2))-(f(x)/x) <=> (f(x)/x)+f΄(x)=1/(x^2) <=> f(x)+xf΄(x)=1/x <=> f(x)+xf΄(x)-(1/x)=0, x ανήκει
Θεωρούμε την συνάρτηση g(x)=xf(x)-ln|x|, x ανήκει R*. Επειδή η f είναι παραγωγίσιμη στο R* τότε και η g είναι παραγωγίσιμη στο R*, οπότε και συνεχής στο R*, με πρώτη παράγωγο
g΄(x)=f(x)+xf΄(x)-(1/x)=0 για κάθε x ανήκει R*
Η g είναι συνεχής και παραγωγίσιμη στο (-οο,0) και ισχύει g(x)=0 για κάθε x ανήκει (-οο,0). Επομένως υπάρχει πραγματική σταθερά c1 έτσι ώστε να ισχύει g(x)=c1 για κάθε x ανήκει (-οο,0). Άρα
g(x)=c1 <=> xf(x)-ln|x|=c1 <=> xf(x)=c1+ln|x| <=> f(x)=(c1+ln|x|)/x
Άρα f(x)=(c1+ln(-x))/x, x<0
Η g είναι συνεχής και παραγωγίσιμη στο (0,+oo) και ισχύει g(x)=0 για κάθε x ανήκει (0,+oo). Επομένως υπάρχει πραγματική σταθερά c1 έτσι ώστε να ισχύει g(x)=c1 για κάθε x ανήκει (0,+oo). Άρα
g(x)=c2 <=> xf(x)-ln|x|=c2 <=> xf(x)=c2+ln|x| <=> f(x)=(c2+ln|x|)/x
Άρα f(x)=(c2+lnx)/x, x>0
Γνωρίζουμε ότι f(1)=e και f(-1)=-e
Έχουμε
f(-1)=-c1 και f(-1)=-e => c1=e
f(1)=c2 και f(1)=1 => c2=e
Άρα
f(x)=(e+ln(-x))/x, x<0
f(x)=(e+lnx)/x, x>0
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Aris90
Εκκολαπτόμενο μέλος


1)για μια συναρτηση f ισχυουν
ι)ειναι συνεχης στο [-α,α],α>0
ιι)ειναι δυο φορες παραγωγισιμη στο (-α,α)
ιιι)f(-α)=f(0)=f(α)
ν.δ.ο οτι υπαρχει ξΕ(-α,α) τετοιο ωστε f''(ξ)=0
2)εστω συναρτηση g(x)=f(x)(x²-1) οπου f(x) συναρτηση παραγωγισιμη δυο φορες στο [-1,1] και η cf διερχεται απο την αρχη 0 του συστηματος των αξονων ν.δ.ο υπαρχει ξΕ(-1,1) τετοιο ωστε g''(ξ)=0
3)δινεται συναρτηση f δυο φορες παραγωγισιμη στο [α,β] α<0<β
ν.δ.ο υπαρχει ξΕ(α,β) τετοι ωστε f''(ξ)=0
ξερω οτι αυτες οι ασκησεις οτι ειναι απλες αλλα επειδη δεν εχω και την καλυτερη σχεση στα μαθηματικα , επειδη ειναι πρωτες που κανω σε αυτο το κεφαλαιο και παλευω αρκετη ωρα θα χρειαστω καποια tips και βλεπουμε
ευχαριστω εκ'των πρωτερων
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Για την πρώτη άσκηση σου δίνει την συνάρτηση στην οποία θα εφαρμόσεις το θεώρημα Rolle οπότε δεν έχει καμία δυσκολία. Για την δεύτερη πρέπει να αποδείξεις ότιεστω η συναρτηση g(x)=e^f(x)(x-a)(x-b) οπου a,bΕR a<b και f(x) συναρτηση συνεχης στο [a,b] και παραγωγισιμη στο (a,b) ν.δ.ο υπαρχει ξΕ(a,b) τετοιο ωστε
f'(ξ)=a+b-2ξ/(ξ-α)(ξ-β)
και τι πρεπει να πω οταν μου λεει ν.δ.ο οτι εφαρμοζεται το θεωρημα rolle για τη συναρτηση
g(x)=f(x)e^-λx λΕR [a,b]
για την πρωτη ασκηση δεν θελω καποια λυση αλλα καποιο καλο tip ειναι η πρωτη με τετοιο ειδους που κανω
Για τις 1) και 2) βρες κατάλληλα διαστήματα όπου θα εφαρμόσεις το Rolle για την συνάρτηση που δίνεται (f και g αντίστοιχα), κάτι το οποίο βασικά στο δίνει στην εκφώνηση. Στην συνέχεια θα χρειαστεί κι άλλο θεώρημα Rolle για τις f' και g'.θελω καποια tips για τις παρακατω ασκησεις
1)για μια συναρτηση f ισχυουν
ι)ειναι συνεχης στο [-α,α],α>0
ιι)ειναι δυο φορες παραγωγισιμη στο (-α,α)
ιιι)f(-α)=f(0)=f(α)
ν.δ.ο οτι υπαρχει ξΕ(-α,α) τετοιο ωστε f''(ξ)=0
2)εστω συναρτηση g(x)=f(x)(x²-1) οπου f(x) συναρτηση παραγωγισιμη δυο φορες στο [-1,1] και η cf διερχεται απο την αρχη 0 του συστηματος των αξονων ν.δ.ο υπαρχει ξΕ(-1,1) τετοιο ωστε g''(ξ)=0
3)δινεται συναρτηση f δυο φορες παραγωγισιμη στο [α,β] α<0<β
ν.δ.ο υπαρχει ξΕ(α,β) τετοι ωστε f''(ξ)=0
ξερω οτι αυτες οι ασκησεις οτι ειναι απλες αλλα επειδη δεν εχω και την καλυτερη σχεση στα μαθηματικα , επειδη ειναι πρωτες που κανω σε αυτο το κεφαλαιο και παλευω αρκετη ωρα θα χρειαστω καποια tips και βλεπουμε
ευχαριστω εκ'των πρωτερων
Για την 3) η δοθείσα σχέση γράφεται
ποιο θεώρημα σου έρχεται στο μυαλό βλέποντας αυτή την σχέση; Πριν απαντήσεις σε όλες τις ασκήσεις βεβαιώσου ότι έχεις διαβάσει και χωνέψει το θεώρημα Rolle, και το θεώρημα της μέσης τιμής. Θα σε βοηθήσει να έχεις και μία εικόνα για την γεωμετρική τους ερμηνεία.
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
aris-bas
Νεοφερμένο μέλος



1)εστω η συναρτηση f : R->R η οποια ειναι παραγωγισιμη τετοια ωστε f(1)=3 και f(x)>=2x+1 για καθε χ ε R.
α) να αποδειξετε οτι η ευθεια y=2x+1 εφαπτεπται της Cf.
β)να βρειτε το οριο
γ) αν η f ειναι συνεχης να αποδειξετε οτι υπαρχει ενα τουλαχιστον χο ε (0,1)τετοιο ωστε f(xo)=2xof'(xo)
2)δινεται η συναρτηση f(x)=αlnx-x-2, x>0 α>0
α)να αποδειξετε οτι:
β)να μελετησετε την f ως προς τη μονοτονια και να αποδειξετε οτι η μεγιστη τιμη της συναρτησης ειναι f(α)
γ)για α=1 αποδειξτε οτι:
ι)η μεγιστη τιμη της f ειναι ελαχιστη
ιι)υπαρχει χο ε (1,e) τετοιο ωστε
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
antwwwnis
Διάσημο μέλος


Για την 1.γεια!μηπως μπορει να βοηθησει κανεις στις παρακατω ασκησεις....???
1)εστω η συναρτηση f : R->R η οποια ειναι παραγωγισιμη τετοια ωστε f(1)=3 και f(x)>=2x+1 για καθε χ ε R.
α) να αποδειξετε οτι η ευθεια y=2x+1 εφαπτεπται της Cf.
β)να βρειτε το οριο
γ) αν η f ειναι συνεχης να αποδειξετε οτι υπαρχει ενα τουλαχιστον χο ε (0,1)τετοιο ωστε f(xo)=2xof'(xo)
2)δινεται η συναρτηση f(x)=αlnx-x-2, x>0 α>0
α)να αποδειξετε οτι:
β)να μελετησετε την f ως προς τη μονοτονια και να αποδειξετε οτι η μεγιστη τιμη της συναρτησης ειναι f(α)
γ)για α=1 αποδειξτε οτι:
ι)η μεγιστη τιμη της f ειναι ελαχιστη
ιι)υπαρχει χο ε (1,e) τετοιο ωστε=\frac { 2-e }{ e-1 } )
α)Βλέπεις ανισότητα; υπάρχει ένα ακρότατο κρυμμένο εκεί μέσα. Είναι και παραγωγίσιμη η f. Εχεις θεώρημα ωστε να βρεις το f'(1)! Οπότε και γραφεις την εφαπτομένη της Cf στο (1,3)
β) συζυγης παρασταση και προκύπτει οριο που μοιαζει με οριο παραγώγου (το f'(1))
γ) (αφου σου λέει ειναι παραγωγισιμη δε χρειαζοταν να αναφερει οτι ειναι και συνεχης)
Rolle, Bolzano, δοκίμασες;
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Λογικά εννοείαφου σου λέει ειναι παραγωγισιμη δε χρειαζοταν να αναφερει οτι ειναι και συνεχης
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος


2)δινεται η συναρτηση f(x)=αlnx-x-2, x>0 α>0
α)να αποδειξετε οτι:
β)να μελετησετε την f ως προς τη μονοτονια και να αποδειξετε οτι η μεγιστη τιμη της συναρτησης ειναι f(α)
γ)για α=1 αποδειξτε οτι:
ι)η μεγιστη τιμη της f ειναι ελαχιστη
ιι)υπαρχει χο ε (1,e) τετοιο ωστε=\frac { 2-e }{ e-1 } )
α) lim(x->0)(-x-2)=-0-2=-2 <=> lim(x->0-)(-x-2)=lim(x->0+)(-x-2)=-2
lim(x->0+)lnx=-oo => lim(x->0+)(αlnx)=-oo εφόσον α>0
Άρα lim(x->0+)f(x)=lim(x->0+)(αlnx-x-2)=-oo
Θεωρούμε τις συναρτήσεις f1(x)=lnx, x>0 και f2(x)=x, x ανήκει R. Η f1 είναι συνεχής και παραγωγίσιμη στο (0,+οο) με πρώτη παράγωγος f1΄(x)=1/x. Η f2 είναι συνεχής και παραγωγίσιμη στο R με πρώτη παράγωγο f2΄(x)=1. Έχουμε:
lim(x->+oo)[f1΄(x)/f2΄(x)]=lim(x->+oo)(1/x)=0
Έχουμε lim(x->+oo)f1(x)=lim(x->+oo)lnx=+oo και lim(x->+oo)f2(x)=lim(x->+oo)x=+oo. Επειδή lim(x->+oo)f1(x)=lim(x->+oo)f2(x)=+oo τότε ο όριο lim(x->+oo)[f1(x)/f2(x)] οδηγεί σε απροσδιόριστη μορφή (+οο)/(+οο). Επομένως σύμφωνα με τον 2ο κανόνα De L' Hospital είναι:
lim(x->+oo)[f1(x)/f2(x)]=lim(x->+oo)[f1΄(x)/f2΄(x)]=0
Επομένως lim(x->+oo)(lnx/x)=0
Έχουμε
lim(x->+oo)[α(lnx/x)-1]=α*0-1=-1, α>0
Επειδή lim(x->+oo)x=+oo και lim(x->+oo)[α(lnx/x)-1]=-1<0 τότε lim(x->+oo)(αlnx-x)=lim(x->+oo)[x(α(lnx/x)-1)]=-oo
Άρα lim(x->+oo)f(x)=lim(x->+oo)(αlnx-x-2)=-oo
β) Η f είναι συνεχής και παραγωγίσιμη στο (0,+οο) με πρώτη παράγωγο f΄(x)=(α/x)-1. Ισχύει f΄(α)=1
Η f είναι συνεχής στο (0,α], παραγωγίσιμη στο (0,α) και ισχύει f΄(x)>0 για κάθε x ανήκει (0,α). Άρα η f είναι γνησίως αύξουσα στο (0,α].
Η f είναι συνεχής στο [α,+οο), παραγωγίσιμη στο (α,+οο) και ισχύει f΄(x)<0 για κάθε x ανήκει (α,+οο). Άρα η f είναι γνησίως φθίνουσα στο [α,+οο).
Επομένως η f παρουσιάζει ολικό μέγιστο στο α με τιμή f(α)=αlnα-α-2, α>0
γ) Θεωρούμε την συνάρτηση g(α)=f(α)=αlnα-α-2, α>0. Η g είναι συνεχής και παραγωγίσιμη στο (0,+οο) με πρώτη παράγωγο
g΄(α)=lnα. Ισχύει g΄(1)=0
(i) Η g είναι συνεχής στο (0,1], παραγωγίσιμη στο (0,1) και ισχύει g΄(x)<0 για κάθε α ανήκει (0,1). Άρα η g είναι γνησίως φθίνουσα στο (0,1]. Η g είναι συνεχής στο [1,+οο), παραγωγίσιμη στο (1,+οο) και ισχύει g΄(x)>0 για κάθε α ανήκει (1,+οο). Άρα η g είναι γνησίως αύξουσα στο [1,+οο).
Επομένως η g παρουσιάζει ολικό ελάχιστο στο α0=1 με τιμή g(1)=-3.
(ii) Για α=1 έχουμε f(x)=lnx-x-2, x>0. Η f είναι συνεχής και παραγωγίσιμη στο (0,+οο) με πρώτη παράγωγο f΄(x)=(1/x)-1, x>0.
Έχουμε f(1)=-3 και f(e)=-e-1. Η f είναι συνεχής στο [1,e] και παραγωγίσιμη στο (1,e). Επομένως σύμφωνα μμε το θεώρημα μέσης τιμής υπάρχει τουλάχιστον ένα x0 ανήκει (1,e) τέτοιο ώστε:
f΄(x0)=(f(e)-f(1))/(e-1)=(2-e)/(e-1)
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
aris-bas
Νεοφερμένο μέλος


γεια!μηπως μπορει να βοηθησει κανεις στις παρακατω ασκησεις....???
1)εστω η συναρτηση f : R->R η οποια ειναι παραγωγισιμη τετοια ωστε f(1)=3 και f(x)>=2x+1 για καθε χ ε R.
α) να αποδειξετε οτι η ευθεια y=2x+1 εφαπτεπται της Cf.
β)να βρειτε το οριο
γ) αν η f ειναι συνεχης να αποδειξετε οτι υπαρχει ενα τουλαχιστον χο ε (0,1)τετοιο ωστε f(xo)=2xof'(xo)
2)δινεται η συναρτηση f(x)=αlnx-x-2, x>0 α>0
α)να αποδειξετε οτι:
β)να μελετησετε την f ως προς τη μονοτονια και να αποδειξετε οτι η μεγιστη τιμη της συναρτησης ειναι f(α)
γ)για α=1 αποδειξτε οτι:
ι)η μεγιστη τιμη της f ειναι ελαχιστη
ιι)υπαρχει χο ε (1,e) τετοιο ωστε=\frac { 2-e }{ e-1 } )
Στην 1) ο αριθμητής του ορίου είναι f(x)-3x.....συγνωμη είχα κανει λάθος
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος


1)εστω η συναρτηση f : R->R η οποια ειναι παραγωγισιμη τετοια ωστε f(1)=3 και f(x)>=2x+1 για καθε χ ε R.
α) να αποδειξετε οτι η ευθεια y=2x+1 εφαπτεπται της Cf.
β)να βρειτε το οριο
γ) αν η f΄ ειναι συνεχης να αποδειξετε οτι υπαρχει ενα τουλαχιστον χο ε (0,1)τετοιο ωστε f(xo)=2xof'(xo)
α) f(x)>=2x+1 <=> f(x)-2x>=1 για κάθε x ανήκει R
Θεωρούμε την συνάρτηση g με τύπο g(x)=f(x)-2x. Επειδή η f είναι παραγωγίσιμη στο R τότε και η g είναι παραγωγίσιμη στο R με πρώτη παράγωγο g΄(x)=f΄(x)-2, x ανήκει R. Έχουμε g(1)=f(1)-2=3-2=1 και g΄(1)=f΄(1)-2.
g(x)>=1 <=> g(x)>=g(1) για κάθε x ανήκει R. Επομένως η g παρουσιάζει ολικό (άρα και τοπικό) ελάχιστο στο x1=1.
Η g είναι ορισμένη στο R, παρουσιάζει τοπικό ελάχιστο στο x1=1 και είναι παραγωγίσιμη σε αυτό. Επομένως σύμφωνα με το θεώρημα του Fermat ισχύει g΄(1)=0 <=> f΄(1)=2
Η εφαπτομένη της Cf στο (1,f(1)) έχει εξίσωση:
y-f(1)=f΄(1)(x-1) <=> y-3=2(x-1) <=> y=2x+1
β) Η συνάρτηση f είναι παραγωγίσιμη στο x0=1. Άρα έχουμε:
lim(x->1)[(f(x)-f(1))/(x-1)]=f΄(1) <=> lim(x->1)[(f(x)-3)/(x-1)]=2
Άρα
lim(x->1)[(f(x)-3)/(SQRT(x)-1)]=lim(x->1)[((f(x)-3)(SQRT(x)+1))/((SQRT(x)-1)(SQRT(x)+1)]=lim(x->1)[((f(x)-3)(SQRT(x)+1))/(x-1)]=lim(x->1)[(f(x)-3)/(x-1)]*lim(x->1)(SQRT(x)+1)=2*(SQRT(1)+1)=2*(1+1)=2*2=4
Θεωρούμε την συνάρτηση F με τύπο F(x)=f(x)-3x, x ανήκει R. Επειδή η f είναι παραγωγίσιμη στο R τότε και η F είναι παραγωγίσιμη στο R με πρώτη παράγωγο F΄(x)=f΄(x)-3. Έχουμε F(1)=f(1)-3=3-3=0 και F΄(1)=f΄(1)-3=2-3=-1. Από τον ορισμό της παραγώγου έχουμε:
lim(x->1)[(F(x)-F(1))/(x-1)]=F΄(1) => lim(x->1)[(f(x)-3x)/(x-1)]=-1
Άρα
lim(x->1)[(f(x)-3x)/(SQRT(x)-1)]=lim(x->1)[((f(x)-3x)(SQRT(x)+1))/((SQRT(x)-1)(SQRT(x)+1)]=
=lim(x->1)[((f(x)-3x)(SQRT(x)+1))/(x-1)]=lim(x->1)[(f(x)-3x)/(x-1)]*lim(x->1)(SQRT(x)+1)=
=(-1)*(SQRT(1)+1)=-(1+1)=-2
γ) Για x=0 έχουμε
f(0)>=1 <=> -f(0)<=-1<0
Θεωρούμε την συνάρτηση h με τύπο h(x)=2xf΄(x)-f(x), x ανήκει R. Επειδή η f΄ είναι συνεχής στο [0,1] τότε και η h είναι συνεχής στο [0,1].
Έχουμε
h(0)=-f(0)<0
h(1)=2f΄(1)-f(1)=2*2-3=4-3=1>0
Άρα h(0)h(1)<0
Η h είναι συνεχής στο [0,1] και ισχύει h(0)h(1)<0. Επομένως σύμφωνα με το θεώρημα Bolzano υπάρχει τουλάχιστον ένα x0 ανήκει (0,1) τέτοιο ώστε h(x0)=0 <=> f(x0)=2x0f΄(x0).
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
χριχρι :)
Νεοφερμένο μέλος


Pleaaaase όποιος μπορεί, μου χει σπάσει τα νεύρα...
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος


Αν f(x)=x^2 x ανήκει R, να αποδείξετε ότι για κάθε α,β ανήκει R ισχύει: f(α)+f(β)≥2f(α+β/2)
Pleaaaase όποιος μπορεί, μου χει σπάσει τα νεύρα...
(α-β)^2>=0 <=> (α^2)+(β^2)-2αβ>=0 <=> (α^2)+(β^2)>=2αβ <=> (α^2)+(β^2)+(α^2)+(β^2)>=(α^2)+(β^2)+2αβ <=>
<=> 2(α^2)+2(β^2)>=(α+β)^2 <=> (α^2)+(β^2)>=((α+β)^2)/2 <=> (α^2)+(β^2)>=2[((α+β)/2)^2] <=> f(α)+f(β)>=2f((α+β)/2)
Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
χριχρι :)
Νεοφερμένο μέλος


(α-β)^2>=0 <=> (α^2)+(β^2)-2αβ>=0 <=> (α^2)+(β^2)>=2αβ <=> (α^2)+(β^2)+(α^2)+(β^2)>=(α^2)+(β^2)+2αβ <=>
<=> 2(α^2)+2(β^2)>=(α+β)^2 <=> (α^2)+(β^2)>=((α+β)^2)/2 <=> (α^2)+(β^2)>=2[((α+β)/2)^2] <=> f(α)+f(β)>=2f((α+β)/2)
Ευχαριστώ πολύ

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
JKaradakov
Τιμώμενο Μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 9 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 227 μέλη διάβασαν αυτό το θέμα:
- hristosdab
- trifasikodiavasma
- haji
- thepigod762
- Mariosm.
- soulatso
- oteletampis
- phleidhs
- Hased Babis
- AggelikiGr
- sir ImPeCaBlE
- veiNqh
- Scandal
- alekos
- Debugging_Demon
- just some guy
- xristosgkm
- ismember
- Apocalypse
- arrow25
- rempelos42
- ggl
- GStef
- QWERTY23
- xrisamikol
- Σωτηρία
- nikoletaz57
- _Aggelos123
- Mariam38
- SlimShady
- strsismos88
- Georgekk
- Lia 2006
- igeorgeoikonomo
- marian
- tsiobieman
- constansn
- Xristosdimitra
- Panagiotis849
- ρενακι 13
- Memetchi
- eukleidhs1821
- Nikkkpat
- Unboxholics
- korlef
- kwstaseL
- Thanos_D
- the purge
- T C
- Giii
- Papachrist
- liaiscool
- Αννα Τσιτα
- globglogabgalab
- Pharmacist01
- thanahss
- abcdefg12345
- nicole1982
- thecrazycretan
- kvstas92
- KingOfPop
- maria301
- papa2g
- stefan
- Κλημεντίνη
- TonyMontanaEse
- Athens2002
- Alexecon1991
- Μάρκος Βασίλης
- Cortes
- το κοριτσι του μαη
- calliope
- ale
- panagiotis G
- Kleanth
- aggelosst9
- BioChemical
- spring day
- nucomer
- Georgia110
- LeoDel
- pink_panther
- Alexandros973
- marsenis
- den antexw allh apotyxia
- KaterinaL
- kiyoshi
- drosos
- Λαμπρινηη
- Bill22
- Chrysablac.
- giorgosp97
- Βλα
- Monster Hunter
- jul25
- xxxtolis
- Stroka
- nicks1999
- totiloz
- Earendil
- mitsakos
- tasost
- lnesb
- ssalex
- Vasilina93
- alan09
- Livaja10
- χημεια4λαιφ
- Viedo
- UncleJ
- Kostakis45
- Infrared
- Zgian
- pepatogourounaki
- hirasawayui
- GeoCommand
- Eleni54
- American Economist
- EiriniS20
- ΘανάσοςG4
- stamoul1s
- Αριάνα123
- uni77
- Libertus
- tasoss
- PanosCh002
- Unseen skygge
- Νικόλας Ραπ.
- cel123
- The Limit Does Not Exist
- don_vito
- suaimhneas
- Αλκης Κ.
- alexrami
- Baggelitsa36
- Νομικάριος13
- spinalgr1990
- d_th
- Adolfo valencia
- Πα.Κ
- Vasilis25
- Johnman97
- Steffie88
- rekcoR
- gwgw_5
- fockos
- Mariahj
- roud
- kostas83
- Cpt.Philips
- Makis45
- Χρησλου
- Panos_02
- Vold
- tymvorixos
- GiorgosAsi
- Neos167
- theodoraooo
- George187
- Άρτεμις Α.
- Μαρία2222
- christos87
- Idontknoww
- jimis2001
- Metamorph
- Γατόπαρδος.
- Johnsk
- mitsos14
- johnsiak
- Elel
- Dreamer_SW
- Γιαννης1987Θεσσ
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki

