Προς gate7:
z1=2+2i (η μία λύση της εξίσωσης) z1^2=z1*z1=(2+2i)(2+2i)=4+4i+4i-4=8i
Ομοίως: z2^2=z2*z2=-8i. z1z2=8
---
z=x+yi=Rez+iImz
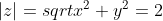
, άρα:
^2+(Imz)^2=2^2)
.
[z1Re(z)+z2Im(z)]*[z1Im(z)+z2Re(z)]=Imz*Rez*z1^2+(Imz)^2*z1*z2+(Rez)^2*z1*z2+Imz*Rez*z2^2=Imz*Rez*8i+(Imz)^2*8+(Rez)^2*8+Imz*Rez*(-8i)=(Imz)^2*8+(Rez)^2*8=8*((Imz)^2+(Rez)^2)=8*4=32
Άσκηση 3

,αφού w=σταθ..
Άρα o z κινείται πάνω στον κύκλο:
,rho=c))
.
Βρες το c εσύ, είναι εύκολο.
Προς Voulitsa:
Επειδή έδωσες την άσκηση σε εικόνα, και επειδή δεν έχω χρόνο αυτή τη στιγμή να γράφω από την αρχή τα πάντα αναλυτικά, δες μία γρήγορη-συνοπτική λύση και αν έχεις απορία ξαναγράφεις και σου απαντώ εγώ ή κπ άλλος:
1)βάζεις στην ανισότητα όπου χ το π/2 και βρίσκεις 3<or=f(π/2)<or=3 => limf(x)=f(π/2)=3
2)πάλι χρησιμοποιείς την ανισότητα: αφαιρείς 3, αντιστρέφεις χωρίς να ξεχάσεις να αλλάξεις τη φορά της ανισότητας και πολλαπλσιάζεις με cos^2(x). Οπότε βρίσκει τα όρια του αριστερού και του δεξιού τυπου της ανισότητας χρησιμοποιώντας Hospital και καταλήγεις στα όρια 2 και 2 οπότε και το ζητούμενο είναι 2.
3)Έχουμε ήδη βρει ότι f(π/2)=3, κάνε τις αντικαταστάσεις, αφού υάρχουν τα όρια και θα βρεις -αν δεν κάνω λάθος: -άπειρο
Το τελευταίο ερώτημα δεν μπορώ να το απαντήσω αν δεν μου δώσεις το που ανήκει το χ (υπάρχει ένα τυπογραφικό λάθος). Ενδεικτικά πάντως σου λέω λύσε την εξίσωση και ακολούθησε τη λογική...