Βοήθεια/Aπορίες στα Μαθηματικά Προσανατολισμού

[DumeNuke]

Ευχαριστώ πολύ!

Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

 

[need4sheed]

δινεται f(x)=(2x-1)^2+|z+xw|,x E R z,w E C και μη μηδενικοι μιγαδικοι ανεξαρτητοι του χ και |z|=1 Επισης ισχυει z^5 + 2(z^4)w-z+w=0 και 2z+w διαφορο του μηδενος.
Αα)ν.α.ο |z+2w|=|z-w|
Aβ)|z+xw| διαφορο του μηδενος για καθε χ Ε R kαι |z+xw|={(|w|^2)x^2+2Re(zwσυζηγης)χ+1}^(1/2)
γ)υπαρχει ενα τουλαχιστον ξΕ(-1,2) ωστε
|w|^2 ξ+Re(z wσυζηγης)=(4-8ξ)|z+ξw|
Β)Αν |w|=1 να εκφρασετε την f(x) χωρις μιγαδικους και να βρειτε το ελαχιστο της

Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

 

[Guest 856924]

Πως γινεται αυτο x^3=-y ?

Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

 

[DumeNuke]

Πως γινεται αυτο x^3=-y ?

(-2)^3=-8
Αρνητικός αριθμός σε περιττή δύναμη δίνει ως αποτέλεσμα περιττό αριθμό και ισχύει:

Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

 

[chester20080]

(-2)^3=-8
Αρνητικός αριθμός σε περιττή δύναμη δίνει ως αποτέλεσμα περιττό αριθμό και ισχύει:

Δηλαδή για παράδειγμα ποιά είναι η λύση της χ^3=-8? Παιδιά γενικά σε αυτά μην ξεχνάτε τις μιγαδικές λύσεις! Τρίτου βαθμού, άρα έχει και δυο μιγαδικές! Γιατί με το που βλέπεις χ^3=1 λες α,οκ,χ=1 (και έτσι πάνε οι μιγαδικές...) Γενικά,με αφορμή αυτό, προσοχή! :-)

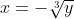
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

 

[methexys]

Δηλαδή για παράδειγμα ποιά είναι η λύση της χ^3=-8? Παιδιά γενικά σε αυτά μην ξεχνάτε τις μιγαδικές λύσεις! Τρίτου βαθμού, άρα έχει και δυο μιγαδικές! Γιατί με το που βλέπεις χ^3=1 λες α,οκ,χ=1 (και έτσι πάνε οι μιγαδικές...) Γενικά,με αφορμή αυτό, προσοχή! :-)

Είναι εκτός ύλης οι μιγαδικές ρίζες. Δηλαδή, όταν μας λένε να λύσουμε μια εξίσωση, δεν γράφουμε και τις μιγαδικές ρίζες.

Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

 

[DumeNuke]

Δηλαδή για παράδειγμα ποιά είναι η λύση της χ^3=-8? Παιδιά γενικά σε αυτά μην ξεχνάτε τις μιγαδικές λύσεις! Τρίτου βαθμού, άρα έχει και δυο μιγαδικές! Γιατί με το που βλέπεις χ^3=1 λες α,οκ,χ=1 (και έτσι πάνε οι μιγαδικές...) Γενικά,με αφορμή αυτό, προσοχή! :-)

Uhm...
Ήταν το πρώτο πράγμα που έγραψα?
(-2)^3=(-2)*(-2)*(-2)=-8
Άρα χ^3=-8 έχει μια πραγματική ρίζα, την -2.
Πάντως, ναι, η εξίσωση x^n=a (όπου a οποιοσδήποτε πραγματικό αριθμός, θετικός ή αρνητικός), έχει:
α) Το πολύ n ρίζες, στο σύνολο των πραγματικών.
β) Ακριβώς n ρίζες, στο σύνολο των μιγαδικών.
Δηλαδή, η x^3=-8 έχει μια πραγματική (-2) και δύο μιγαδικές ρίζες.

Είναι εκτός ύλης οι μιγαδικές ρίζες. Δηλαδή, όταν μας λένε να λύσουμε μια εξίσωση, δεν γράφουμε και τις μιγαδικές ρίζες.

Στην Ανάλυση, ναι, ασχολούμαστε με τους πραγματικούς αριθμούς και δεν ψάχνουμε για μιγαδικές ή φανταστικές ρίζες. Αλλά, στο 2ο θέμα, άμα ζητηθεί να λυθεί μια εξίσωση... Λογικό και επόμενο είναι να ζητήσουν μιγαδικές ρίζες.

Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

 

[chester20080]

Παιδιά απλά το έγραψα σαν παρατήρηση, να το θυμηθούν οι υποψήφιοι ;-)

Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

 

[Guest 856924]

(-2)^3=-8
Αρνητικός αριθμός σε περιττή δύναμη δίνει ως αποτέλεσμα περιττό αριθμό και ισχύει:

δε μπορει να ναι και x=κυβικη ριζα -y ?

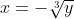
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

 

[dimidimi]

γεια σας παιδια! χρειαζομαι μια βοηθεια εδω! εχουμε οτι f(g(x)) ειναι 1-1! να δειξω πως η g ειναι και αυτη 1-1! εχω κολλησει..καμια βοηθεια?

Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

 

[DumeNuke]

δε μπορει να ναι και x=κυβικη ριζα -y ?

Προσωπικά, δεν με ενοχλεί να δω γραμμένη κυβικη ρίζα αρνητικού αριθμού. Όμως υπάρχει ένας (χαζός) κανόνας που λέει ότι κάτω από ρίζα μπαίνουν μόνο θετικοί (ή έστω μηδενικοί) αριθμοί.
Παράδειγμα:
Η δίνει λύση στο σύνολο των πραγματικών, αλλά είναι λάθος σαν έκφραση.
Η δίνει λύση +/-2i, στο σύνολο των μιγαδικών, αλλά είναι λάθος σαν έκφραση.
Παρόλο που υπάρχουν ρίζες αρνητικών αριθμών, θεωρείται λάθος να το γράψεις...

Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

 

[dimidimi]

γεια σας παιδια! χρειαζομαι μια βοηθεια εδω! εχουμε οτι f(g(x)) ειναι 1-1! να δειξω πως η g ειναι και αυτη 1-1! εχω κολλησει..καμια βοηθεια?

καμια ιδεα?

Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

 

[photon]

γεια σας παιδια! χρειαζομαι μια βοηθεια εδω! εχουμε οτι f(g(x)) ειναι 1-1! να δειξω πως η g ειναι και αυτη 1-1! εχω κολλησει..καμια βοηθεια?

Με τον ορισμο: g(x1)=g(x2)=>f(g(x1))=f(g(x2))=>x1=x2 αρα ειναι 1-1

Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

 

[nPb]

καμια ιδεα?

Προσπάθησε να αναλύεις τα δεδομένα πριν προσπαθήσεις την επίλυση. Τι σημαίνει ότι σου δίνει υπόθεση: έστω ότι f(g(x)) είναι "1-1"; Αν το αναλύσεις εξ' ορισμού τότε καταλήγεις σ' αυτό που έγραψε ο photon.

Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

 

[dimidimi]

ευχαριστω πολυ! και τωρα..με βαση αυτά τα δεδομενα θελει να αποδειξω πως g(f(x)+x^3-x)=g(f(x)+2x-1) οτι εχει 2 ακριβως θετικες ριζες και 1 αρνητικη! ποια μεθοδο χρησιμοποιώ?

Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

 

[DumeNuke]

ευχαριστω πολυ! και τωρα..με βαση αυτά τα δεδομενα θελει να αποδειξω πως g(f(x)+x^3-x)=g(f(x)+2x-1) οτι εχει 2 ακριβως θετικες ριζες και 1 αρνητικη! ποια μεθοδο χρησιμοποιώ?

Ξεκίνα με το γεγονός ότι η g είναι συνάρτηση "1-1" και θα βγει.

Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

 

[dimidimi]

Ξεκίνα με το γεγονός ότι η g είναι συνάρτηση "1-1" και θα βγει.

μου βρηκε!! ευχαριστω παρα πολυ

εχω και μια τελευταια...και σορρυ για την ταλαιπωρια! η εξισωση f(x)=a^x + (a^2-a)x - a^2, 0<a<>1 να αποδειξω οτι γνησιως μονοτονη. την παραγωντοποιησα αλλα δεν εβγαλα καποιο συμπερασμα για την μονοτονια τησ

Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

 

[dimidimi]

εχω και μια τελευταια...και σορρυ για την ταλαιπωρια! η εξισωση f(x)=a^x + (a^2-a)x - a^2, 0<a<>1 να αποδειξω οτι γνησιως μονοτονη. την παραγωντοποιησα αλλα δεν εβγαλα καποιο συμπερασμα για την μονοτονια τησ

Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

 

[rebel]

Δες τι γίνεται για τις περιπτώσεις και .

Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

 

[methexys]

Στην Ανάλυση, ναι, ασχολούμαστε με τους πραγματικούς αριθμούς και δεν ψάχνουμε για μιγαδικές ή φανταστικές ρίζες. Αλλά, στο 2ο θέμα, άμα ζητηθεί να λυθεί μια εξίσωση... Λογικό και επόμενο είναι να ζητήσουν μιγαδικές ρίζες.

E,ναι,προφανώς για την ανάλυση αναφέρομαι, γιατί παλιά είχα δει κάποιες ασκήσεις που έπρεπε να γράψεις μιγαδικές ρίζες, αν και δεν τις ζητούσε, και μας είπαν ότι ήταν εκτός ύλης αυτά. Αν τις βρω θα τις δημοσιεύσω εδώ για να καταλάβετε τι εννοώ.

Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.