Αννα Τσιτα
Νεοφερμένο μέλος
Η Αννα Τσιτα αυτή τη στιγμή δεν είναι συνδεδεμένη. Είναι 20 ετών. Έχει γράψει 40 μηνύματα.

23-02-21

20:16
Γεια σας μπορει καποιος να μου λυσει αυτην την ανισωση; Ειναι για αυριο! Ευχαριστω...
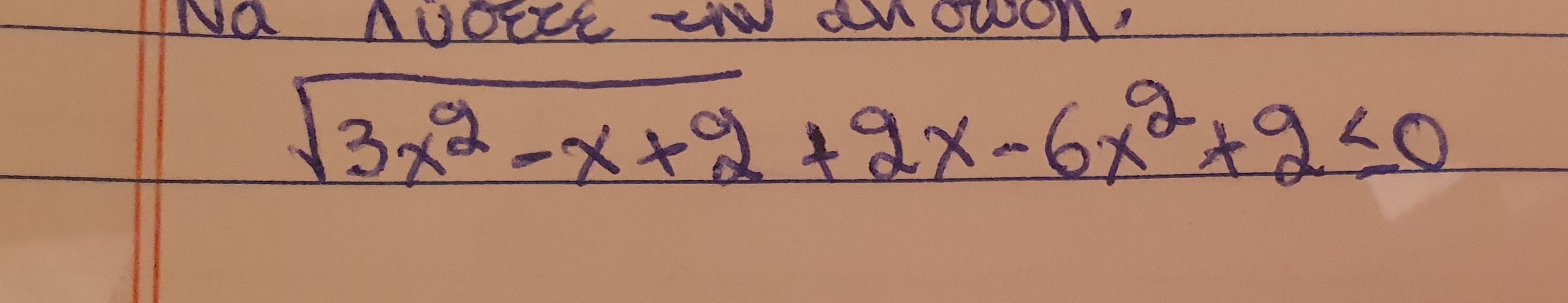

23-02-21

20:21
Μπορείς να βρεις την λύση απο την εφαρμογή photomath. Εξηγεί και τα βήματα.Γεια σς μπορει καποιος να μου λυσει αυτην την ανισωση; Ειναι για αυριο! Ευχαριστω...
Αννα Τσιτα
Νεοφερμένο μέλος
Η Αννα Τσιτα αυτή τη στιγμή δεν είναι συνδεδεμένη. Είναι 20 ετών. Έχει γράψει 40 μηνύματα.

23-02-21

21:33
Ναι προσπάθησα να τη βρω από εκεί άλλα δεν την καταλαβαίνω αν μπορεί κάποιος να με βοηθήσει παρακαλώ είναι επείγον!Μπορείς να βρεις την λύση απο την εφαρμογή photomath. Εξηγεί και τα βήματα.
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 26 ετών, Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 12.124 μηνύματα.

23-02-21

23:07
Γεια σου. Δες παρακάτω :
-6x² + 2x + 2 + sqrt(3x² - x + 2) <= 0
sqrt(3x² - x + 2) <= +6x² - 2x - 2
Το υπόριζο δεν παίρνει ποτέ για καμία τιμή του x ούτε αρνητικές ούτε μηδενικές τιμές . Άρα το αριστερό μέλος είναι πάντα θετικό. Επομένως ,και το δεξί μέλος εφόσον είναι μεγαλύτερο η ίσο, πρέπει οπωσδήποτε να είναι επίσης θετικό. Βάσει αυτών και δεδομένου οτι η g(x) = x² είναι γνησίως αύξουσα(για x>0), θα πρέπει :
[sqrt(3x² - x + 2)]² <= [6x² - 2x - 2]² =>
3x²-x+2 <= [6x²-(2x+2)]² =>
3x²-x+2 <= 36x^4 - 2(2x+2)6x² + (2x+2)² =>
3x²-x+2 <= 36x^4 - 2(2x+2)6x² + 4x²+8x+4 =>
3x²-x+2 <= 36x^4 - 24x³ -24x² + 4x²+8x+4 =>
36x⁴ - 24x³ - 23x² + 9x + 2 >= 0
Το οποίο σου λέω εκ των προτέρων οτι έχει ρίζες 1 και 0,5 με παρατήρηση. Κάνε λοιπόν την γνωστή παραγοντοποίηση πολυωνύμου ώστε να σου μείνει ένα δευτέρου βαθμού πολυώνυμο που είναι πολύ εύκολο πλέον να βρεις τις ρίζες του. Συνολικά θα βρεις 4 ρίζες πάντως(η 1 η 0,5 και οι 2 που θα βρεις απο το πολυώνυμο δευτέρου βαθμού που θα προκύψει με horner).
Θα δεις οτι μόνο οι τιμές απο την δεξιότερη ρίζα προς το +οο και αυτές απο την αεριστερότερη ρίζα εως το -οο ικανοποιούν την ανίσωση. Το παραπάνω πολυώνυμο είναι επίσης θετικό και μεταξύ των δυο ενδιάμεσων ριζών(D & E στην κάτω εικόνα) ,αλλά το διάστημα απορρίπτεται γιατί ξεκαθαρίσαμε οτι για αυτές τις τιμές θα πρέπει το πολυώνυμο 6x²-2x-2 να είναι θετικό . Το εξηγώ λίγο ακόμα παρακάτω για να είμαι σίγουρος οτι θα το καταλάβεις.
Τα παραπάνω τα βλέπεις συνοπτικά στην εικόνα :
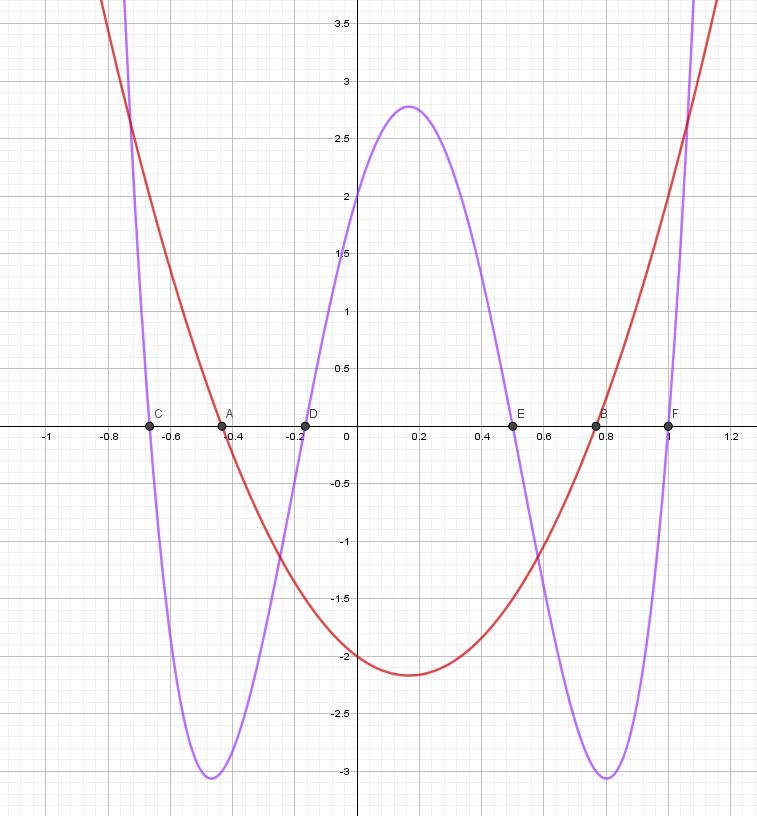
Το μωβ είναι το 36x⁴ - 24x³ - 23x² + 9x + 2 και το κόκκινο το +6x² - 2x - 2 . Ξεκάθαρα οι τιμές μεταξύ των ριζών D και E του πολυωνύμου 36x⁴ - 24x³ - 23x² + 9x + 2 είναι θετικές αλλά περιέχονται στο διάστημα μεταξύ των ριζών A και B του πολυωνύμου +6x² - 2x - 2 στο οποίο διάστημα όμως,λαμβάνει αρνητικές τιμές(και δεν αποτελεί επομένως λύσεις τις ανίσωσης μας βάσει του συλλογισμού που κάναμε στην αρχή).
Θυμήσου οτι οι περιορισμοί ήταν δυο,το +6x² - 2x - 2>0 και τον δεύτερο τον πήραμε απο την απαίτηση 36x⁴ - 24x³ - 23x² + 9x + 2>= 0 . Μόνο οι τιμές του x που ικανοποιούν και τις δυο αυτές απαιτήσεις είναι πραγματικές λύσεις της αρχικής ανίσωσης.
Ελπίζω να βοήθησα .
.
-6x² + 2x + 2 + sqrt(3x² - x + 2) <= 0
sqrt(3x² - x + 2) <= +6x² - 2x - 2
Το υπόριζο δεν παίρνει ποτέ για καμία τιμή του x ούτε αρνητικές ούτε μηδενικές τιμές . Άρα το αριστερό μέλος είναι πάντα θετικό. Επομένως ,και το δεξί μέλος εφόσον είναι μεγαλύτερο η ίσο, πρέπει οπωσδήποτε να είναι επίσης θετικό. Βάσει αυτών και δεδομένου οτι η g(x) = x² είναι γνησίως αύξουσα(για x>0), θα πρέπει :
[sqrt(3x² - x + 2)]² <= [6x² - 2x - 2]² =>
3x²-x+2 <= [6x²-(2x+2)]² =>
3x²-x+2 <= 36x^4 - 2(2x+2)6x² + (2x+2)² =>
3x²-x+2 <= 36x^4 - 2(2x+2)6x² + 4x²+8x+4 =>
3x²-x+2 <= 36x^4 - 24x³ -24x² + 4x²+8x+4 =>
36x⁴ - 24x³ - 23x² + 9x + 2 >= 0
Το οποίο σου λέω εκ των προτέρων οτι έχει ρίζες 1 και 0,5 με παρατήρηση. Κάνε λοιπόν την γνωστή παραγοντοποίηση πολυωνύμου ώστε να σου μείνει ένα δευτέρου βαθμού πολυώνυμο που είναι πολύ εύκολο πλέον να βρεις τις ρίζες του. Συνολικά θα βρεις 4 ρίζες πάντως(η 1 η 0,5 και οι 2 που θα βρεις απο το πολυώνυμο δευτέρου βαθμού που θα προκύψει με horner).
Θα δεις οτι μόνο οι τιμές απο την δεξιότερη ρίζα προς το +οο και αυτές απο την αεριστερότερη ρίζα εως το -οο ικανοποιούν την ανίσωση. Το παραπάνω πολυώνυμο είναι επίσης θετικό και μεταξύ των δυο ενδιάμεσων ριζών(D & E στην κάτω εικόνα) ,αλλά το διάστημα απορρίπτεται γιατί ξεκαθαρίσαμε οτι για αυτές τις τιμές θα πρέπει το πολυώνυμο 6x²-2x-2 να είναι θετικό . Το εξηγώ λίγο ακόμα παρακάτω για να είμαι σίγουρος οτι θα το καταλάβεις.
Τα παραπάνω τα βλέπεις συνοπτικά στην εικόνα :
Το μωβ είναι το 36x⁴ - 24x³ - 23x² + 9x + 2 και το κόκκινο το +6x² - 2x - 2 . Ξεκάθαρα οι τιμές μεταξύ των ριζών D και E του πολυωνύμου 36x⁴ - 24x³ - 23x² + 9x + 2 είναι θετικές αλλά περιέχονται στο διάστημα μεταξύ των ριζών A και B του πολυωνύμου +6x² - 2x - 2 στο οποίο διάστημα όμως,λαμβάνει αρνητικές τιμές(και δεν αποτελεί επομένως λύσεις τις ανίσωσης μας βάσει του συλλογισμού που κάναμε στην αρχή).
Θυμήσου οτι οι περιορισμοί ήταν δυο,το +6x² - 2x - 2>0 και τον δεύτερο τον πήραμε απο την απαίτηση 36x⁴ - 24x³ - 23x² + 9x + 2>= 0 . Μόνο οι τιμές του x που ικανοποιούν και τις δυο αυτές απαιτήσεις είναι πραγματικές λύσεις της αρχικής ανίσωσης.
Ελπίζω να βοήθησα
 .
.Αννα Τσιτα
Νεοφερμένο μέλος
Η Αννα Τσιτα αυτή τη στιγμή δεν είναι συνδεδεμένη. Είναι 20 ετών. Έχει γράψει 40 μηνύματα.

24-02-21

15:18
Γεια σας ανεβασα χθες μια ανισωση και μου την ελυσε ενας κυριος, τον οποιο ευχαριστω πολυ. Το θεμα ειναι οτι παω πρωτη λυκειου και ο τροπος με τον οποιο την ελυσε δεν ηταν κατανοητος. Σας παρακαλω αν μπορει να με βοηθησει καποιος θα ημουν ευγνωμων.
pink_panther
Εκκολαπτόμενο μέλος
Ο pink_panther αυτή τη στιγμή δεν είναι συνδεδεμένος. Έχει γράψει 172 μηνύματα.

24-02-21

15:41
Ο κύριος τα έγραψε πολύ αναλυτικά. Για να μην κατάλαβες σημαίνει ότι έχεις αφήσει κενά. Κάνε ένα ξεσκόνισμα τη θεωρία από την αρχή και θα βρεις την άκρη.
Αννα Τσιτα
Νεοφερμένο μέλος
Η Αννα Τσιτα αυτή τη στιγμή δεν είναι συνδεδεμένη. Είναι 20 ετών. Έχει γράψει 40 μηνύματα.

24-02-21

15:46
Ναι δεν ειπα οτι τα εγραψε λαθος, απλα ειπα οτι καποιους ορους οπως horner, αυξουσα, g, sqrt ( αν δεν κανω λαθος ), δεν τους εχω ξανακουσει...Ο κύριος τα έγραψε πολύ αναλυτικά. Για να μην κατάλαβες σημαίνει ότι έχεις αφήσει κενά. Κάνε ένα ξεσκόνισμα τη θεωρία από την αρχή και θα βρεις την άκρη.
Guest 030894
Επισκέπτης
αυτή τη στιγμή δεν είναι συνδεδεμέν. Δεν έχει γράψει κανένα μήνυμα.

24-02-21

15:47
sqrt ειναι η τετραγωνικη ριζα. Horner και αυξουσα ειναι στην υλη της δευτερας λυκειου οντως
Αννα Τσιτα
Νεοφερμένο μέλος
Η Αννα Τσιτα αυτή τη στιγμή δεν είναι συνδεδεμένη. Είναι 20 ετών. Έχει γράψει 40 μηνύματα.

24-02-21

15:48
Ενταξει ευχαριστω που τουλαχιστον καποιος καταλαβε τους προβληματισμους μου...sqrt ειναι η τετραγωνικη ριζα. Horner και αυξουσα ειναι στην υλη της δευτερας λυκειου οντως
Cade
Πολύ δραστήριο μέλος
Ο Cade αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Απόφοιτος λυκείου. Έχει γράψει 872 μηνύματα.

24-02-21

15:52
Καλησπέρα.

Υποθέτω πως ξέρεις πως να συνεχίσεις..
Υποθέτω πως ξέρεις πως να συνεχίσεις..
Αννα Τσιτα
Νεοφερμένο μέλος
Η Αννα Τσιτα αυτή τη στιγμή δεν είναι συνδεδεμένη. Είναι 20 ετών. Έχει γράψει 40 μηνύματα.

24-02-21

15:55
Ναι ναι σας ευχαριστω πολυ για τον χρονο σας! Ευχομαι καλη συνεχεια!
Οι λυσεις ειναι ( -οο, -τρια δευτερα ] ενωση [ 2,+οο ), ετσι δεν ειναι;
Cade
Πολύ δραστήριο μέλος
Ο Cade αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Απόφοιτος λυκείου. Έχει γράψει 872 μηνύματα.

24-02-21

21:08
Όχι, αυτά που βρήκες είναι για το ω. Θυμισου τι θέσαμε ω. Δεν βρήκες ακόμα τα διαστηματα στα οποία ανήκει το χ.Οι λυσεις ειναι ( -οο, -τρια δευτερα ] ενωση [ 2,+οο ), ετσι δεν ειναι;
Αννα Τσιτα
Νεοφερμένο μέλος
Η Αννα Τσιτα αυτή τη στιγμή δεν είναι συνδεδεμένη. Είναι 20 ετών. Έχει γράψει 40 μηνύματα.

24-02-21

21:09
Και αυτο πώς θα το κανω; ( συγγνωμη που σε ξανα ενοχλω αλλα εχω μπερδευτει πολυ με αυτην την ασκηση )...Όχι, αυτά που βρήκες είναι για το ω. Θυμισου τι θέσαμε ω. Δεν βρήκες ακόμα τα διαστηματα στα οποία ανήκει το χ.
Cade
Πολύ δραστήριο μέλος
Ο Cade αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Απόφοιτος λυκείου. Έχει γράψει 872 μηνύματα.

24-02-21

21:20
Τώρα βρίσκεις σε ποια διαστήματα το Χ είναι θετικό/ίσο με μηδέν και τελείωσες
Αννα Τσιτα
Νεοφερμένο μέλος
Η Αννα Τσιτα αυτή τη στιγμή δεν είναι συνδεδεμένη. Είναι 20 ετών. Έχει γράψει 40 μηνύματα.

24-02-21

21:24
Ωραια, οποτε το χ ανηκει ( -οο, -δυο τριτα ] ενωση [ 1, +οο ), σωστα; ( σε ευχαριστω πολυ για τον χρονο σου...)View attachment 76395
Τώρα βρίσκεις σε ποια διαστήματα το Χ είναι θετικό/ίσο με μηδέν και τελείωσες
Slytherin
Πολύ δραστήριο μέλος
Ο Slytherin αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 40 ετών και Μεταπτυχιούχος. Έχει γράψει 1.116 μηνύματα.

25-02-21

07:54
Εγώ δεν έχω ιδέα  . Όταν πήγαινα σχολείο πήγαινα θεωρητική και διαβάζω πως είναι α λυκείου αυτά. Φαντάζομαι Άλγεβρα. Δεν θυμάμαι τίποτα.
. Όταν πήγαινα σχολείο πήγαινα θεωρητική και διαβάζω πως είναι α λυκείου αυτά. Φαντάζομαι Άλγεβρα. Δεν θυμάμαι τίποτα.
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.965 μηνύματα.

25-02-21

15:05
παντως αυτη η ασκηση δεν εχει και μεγαλο νοημα.ισα ισα σε κανει να αντιπαθησεις τα μαθηματικα.μια αρρητη ανισωση με πραξεις πραξεις και παλι πραξεις και υποπεριπτωσεις.απλα απαραδεκτος ο καθηγητης που βαλε τετοια ασκηση
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 26 ετών, Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 12.124 μηνύματα.

25-02-21

17:10
παντως αυτη η ασκηση δεν εχει και μεγαλο νοημα.ισα ισα σε κανει να αντιπαθησεις τα μαθηματικα.μια αρρητη ανισωση με πραξεις πραξεις και παλι πραξεις και υποπεριπτωσεις.απλα απαραδεκτος ο καθηγητης που βαλε τετοια ασκηση
Ηρέμησε λίγο βρε Ευκλείδη,όποια άσκηση και να δεις λες τους καθηγητές απαράδεκτους λες και τους ξέρεις τους ανθρώπους
 . Οι ασκήσεις είναι toy problems και είναι λογικό στην α λυκείου να μπαίνουν τέτοιες, γιατί αργότερα στην Β και στην Γ, έχοντας λύσει τόσο περίπλοκες,οι μαθητές θα παίζουν στα δάχτυλα τις πιο απλές που θα προκύπτουν αρκετά συχνά.
. Οι ασκήσεις είναι toy problems και είναι λογικό στην α λυκείου να μπαίνουν τέτοιες, γιατί αργότερα στην Β και στην Γ, έχοντας λύσει τόσο περίπλοκες,οι μαθητές θα παίζουν στα δάχτυλα τις πιο απλές που θα προκύπτουν αρκετά συχνά.eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.965 μηνύματα.

25-02-21

17:19
απλα δεν νομιζω οτι οφελουν τετοιου τυπου ασκησεις αν και νομιζω οι αρρητες ανισωσεις γινονται στη β λυκειουΗρέμησε λίγο βρε Ευκλείδη,όποια άσκηση και να δεις λες τους καθηγητές απαράδεκτους λες και τους ξέρεις τους ανθρώπους. Οι ασκήσεις είναι toy problems και είναι λογικό στην α λυκείου να μπαίνουν τέτοιες, γιατί αργότερα στην Β και στην Γ, έχοντας λύσει τόσο περίπλοκες,οι μαθητές θα παίζουν στα δάχτυλα τις πιο απλές που θα προκύπτουν αρκετά συχνά.
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 26 ετών, Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 12.124 μηνύματα.

25-02-21

17:30
Εσένα σίγουρα όχι γιατί είναι κάποια ages πίσω απο τότε που τα διδάχθηκες πρώτη φοράαπλα δεν νομιζω οτι οφελουν τετοιου τυπου ασκησεις αν και νομιζω οι αρρητες ανισωσεις γινονται στη β λυκειου
 . Τούτη όμως είναι μικρούλα ακόμα, πάει α λυκείου, επομένως έχει όφελος να ασχοληθεί με τέτοιες ασκήσεις τώρα. Σκέψου οτι για ένα νέο παιδί που τα βλέπει πρώτη φορά μπορεί να είναι πολύ περίεργα όλα αυτά. Αλλά δες το και γενικά, ένα μεγάλο μέρος των μαθηματικών είναι να αναγνωρίζεις ήδη γνωστές δομές μέσα σε άλλες, πιθανώς πιο περίπλοκες. Αυτό κάνει το μάτι σου πιο κοφτερό και φυσικά δυναμώνει τις γνώσεις σου πάνω στις απλούστερες δομές. Να το πω πιο λαικά, εαν έχεις δει το ίδιο πράγμα και απο την κανονική και απο την "ανάποδη",ε πλέον το έχεις καταλάβει πέραν πάσης αμφιβολίας. Αυτή η άσκηση πιστεύω το εξυπηρετεί αυτό.
. Τούτη όμως είναι μικρούλα ακόμα, πάει α λυκείου, επομένως έχει όφελος να ασχοληθεί με τέτοιες ασκήσεις τώρα. Σκέψου οτι για ένα νέο παιδί που τα βλέπει πρώτη φορά μπορεί να είναι πολύ περίεργα όλα αυτά. Αλλά δες το και γενικά, ένα μεγάλο μέρος των μαθηματικών είναι να αναγνωρίζεις ήδη γνωστές δομές μέσα σε άλλες, πιθανώς πιο περίπλοκες. Αυτό κάνει το μάτι σου πιο κοφτερό και φυσικά δυναμώνει τις γνώσεις σου πάνω στις απλούστερες δομές. Να το πω πιο λαικά, εαν έχεις δει το ίδιο πράγμα και απο την κανονική και απο την "ανάποδη",ε πλέον το έχεις καταλάβει πέραν πάσης αμφιβολίας. Αυτή η άσκηση πιστεύω το εξυπηρετεί αυτό.Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 0 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 47 μέλη διάβασαν αυτό το θέμα:
- _Aggelos123
- Cat lady
- sweater weather
- Σωτηρία
- Libertus
- Scandal
- Αννα Τσιτα
- Georgekk
- spring day
- barkos
- rhymeasylum
- igeorgeoikonomo
- SlimShady
- Alexandros36k
- Lathy
- nucomer
- eukleidhs1821
- T C
- Unboxholics
- Slytherin
- KaterinaL
- tsiobieman
- LeoDel
- pink_panther
- το κοριτσι του μαη
- Satan Claus
- Giii
- χημεια4λαιφ
- panagiotis23
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki



