3v@Ki
Εκκολαπτόμενο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
qwerty111
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
vimaproto
Πολύ δραστήριο μέλος


Θα περιγράψω την άσκηση γιατί οι πράξεις είναι πολλέςκαλησπέρα!!! μπορειτε να με βοηθησετε με την παρακάτω ασκηση?
Φωτεινή ακτίνα διερχόμενη από το σημείο Σ (2, 3) και προσπίπτουσα στην ευθεία x + y + 1 = 0, μετά την ανάκλασή της διέρχεται από το σημείο
Μ (1, 1). Να βρεθούν οι εξισώσεις της προσπίπτουσας και της ανακλόμενης ακτίνας.
Οι εξισώσεις (ε1) y=λx+k και διερχόμενη από το Σ(2,3) γίνεται y=λx+3-2λ
η (ε2) y=μx+ρ και διερχόμενη από το (1,1) γίνεται y=μx+1-μ
Η κάθετος στην χ+y+1=0 είναι y=x+θ και διέρχεται από το σημείο τομής των ε1 και ε2 που ανήκει στην x+y+1=0
Η γωνία πρόσπτωσης είναι ίση με την γωνία ανάκλασης δηλ η γωνίες των ε1 και ε2 με την κάθετο είναι ίσες και από τη σχέση εφ(Α-Β)=(εφΑ-εφΒ)/(1+εφΑεφΒ) όπου οι εφαπτομένη ισούται με τον συντελεστή κατεύθυνσης βρίσκω λμ=1
ετσι η ε2 γράφεται y=(x/λ) +1-(1/λ) Λύνω το σύστημα των ε1 και ε2 και τις τιμές των χ,y τις αντικαθιστώ στην x+y+1=0 και προκύπτει μια εξίσωση ως προς λ από την οποία βρίσκω τον λ , άρα και τις ε1, ε2.
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
elissavet21
Νεοφερμένο μέλος



Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
vimaproto
Πολύ δραστήριο μέλος


Ρίξε μια ματιά στα μαθηματικά της Β' Γυμνασίου στις εξισώσεις. Υπάρχει το σύμβολο της ισοδυναμίας? Παρακολούθησε τα σχολικά βιβλία των μαθηματικών των τελευταίων 25 ετών. Θα δεις πολλές διαφοροποιήσεις. Τερτίπια? Δεν ξέρω.Με αυτό το σκεπτικό δεν θα έπρεπε να υπάρχει καθόλου η ισοδυναμία.
Μου έρχεται στο νου μου ο ορισμός της τετραγωνικής και της κυβικής ρίζας. Σκέψου το.
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


και η εξίσωσή της
Οι συντεταγμένες του Κ επαληθεύουν τις (1),(2) από το σύστημα των οποίων βρίσκουμε
Έτσι οι ευθείες των ακτίνων βρίσκουμε ότι έχουν εξισώσεις
--------------------------------------------------------------------------------------------------------------------------------------------------------
O querty λέει απλά ότι στο σημείοεγω ξερω οτι η ισοδυναμια χρειαζεται οταν για να αποδειξεις κατι ξεκινας με την υποθεση οτι ετσω οτι ισχυει αυτο που θες να αποδειξεις και καταληξεις σε κατι που επισης ισχυει αλλα βαζεις ισοδυναμιες γιατι τελικα πρεπει να γυρισεις πισω ξανα στην αρχικη υποθεση που εκανες...εγω δεν εκανα την υποθεση "εστω οτι την επαληθευει" αλλα κατεληξα με μια σειρα λογικων πραξεων στο οτι την επαληθευει
οι συνεπαγωγές θα έπρεπε να είναι ανάποδα αφού μας ενδιαφέρει η προς τα αριστερά και όχι η προς τα δεξιά κατεύθυνση. Διάβασε αυτό το άρθρο και θα καταλάβεις πως το εννοείπου ιχυει για καθε
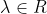
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
kiriazispao4ever
Δραστήριο μέλος


Μία άλλη προσέγγιση η οποία έχει κι αυτή κάποιες πράξεις. Έστωτο σημείο πρόσπτωσης (το σημείο που προσπίπτει και ανακλάται η ακτίνα). Τότε η εξίσωση της καθέτου της ευθείας
στο Κ είναι
. Θεωρούμε το συμμετρικό σημείο του Μ ως προς την (ε), το οποίο καλούμε Μ'. Το Μ' θα ανήκει στην προσπίπτουσα ακτίνα και μετά από πράξεις (κλασσική μέθοδος εύρεσης συμμετρικού σημείου ως προς ευθεία) βρίσκουμε ότι θα έχει συντεταγμένες
. Άρα ο συντελεστής διεύθυνσης της προσπίπτουσας (KΣ) θα είναι
και η εξίσωσή της
Οι συντεταγμένες του Κ επαληθεύουν τις (1),(2) από το σύστημα των οποίων βρίσκουμε
Έτσι οι ευθείες των ακτίνων βρίσκουμε ότι έχουν εξισώσειςκαι
--------------------------------------------------------------------------------------------------------------------------------------------------------
O querty αναφέρεται σε αυτό το σημείο μάλλον
που ιχυει για καθε
και λέει απλά ότι οι συνεπαγωγές θα έπρεπε να είναι ανάποδα αφού μας ενδιαφέρει η προς τα αριστερά και όχι η προς τα δεξιά κατεύθυνση.
η λυση σου μοιαζει με αυτα που κανουμε στην ευθεια στην β λυκειου

γραφω και διαγωνισμα την τριτη...και δεν την εχω πολυκαταλαβει

αλλα μοιάζει πάντως

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
maria98125
Νεοφερμένο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
maria98125
Νεοφερμένο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
antwwwnis
Διάσημο μέλος


Προφανώς δε θα βρεις μια τιμή του ''αγνώστου''. Αλλά ένα σύνολο τιμών που μπορεί να πάρει ώστε να μη μηδενίζεται η ορίζουσα.ναι το σκέφτηκα αυτό.. αλλά πρέπει να βρούμε τον άγνωστο
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
maria98125
Νεοφερμένο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
maria98125
Νεοφερμένο μέλος


Πήρα τα διανύσματα ΑΒ(2,λ-3) και ΑΓ(λ,λ-3) και η ορίζουσα μου βγήκε (-λ(τετράγωνο)+2λ) το οποίο έχει διακρίνουσα -7
Τι έχω κάνει λάθος?
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
maria98125
Νεοφερμένο μέλος


Στο παράδειγμα που ανέφερα το σύνολο που λέει ο Αντώνης θα ήταν το. Αν το λ ανήκει σε αυτό το σύνολο τότε τα σημεία σχηματίζουν τρίγωνο.
Και πώς θα αποδείξουμε ότι ο άγνωστος ανήκει σε αυτό το σύνολο?
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
maria98125
Νεοφερμένο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Και πώς θα αποδείξουμε ότι ο άγνωστος ανήκει σε αυτό το σύνολο?
Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
maria98125
Νεοφερμένο μέλος




Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
- Status
- Το θέμα δεν είναι ανοιχτό για νέες απαντήσεις.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 1 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 16 μέλη διάβασαν αυτό το θέμα:
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki



