Βοήθεια/Απορίες στα Μαθηματικά Γενικής Παιδείας

exc · 12-12-10

Αρχική Δημοσίευση από Dias:
Ο.Κ. η έκθεση είναι το αδύνατο σημείο μου. Νόμιζα ότι ΩΣ και ΣΑΝ είναι το ίδιο. Δεν είναι ε?
Φαντάζομαι στις πανελλήνιες δεν θα μου έκοβαν βαθμό στα μαθηματικά από κάτι τέτοιο ε?

Στο πρώτο ερώτημά σου η απάντηση είναι προφανής: ΌΧΙ.
Το "σαν" χρησιμοποιείται για παρομοιώσεις όταν κάτι δεν είναι έτσι.
Είναι γνωστή η γκάφα του τότε υπουργού παιδείας Αρσένη που είπε "Σας μιλώ ΣΑΝ υπουργός παιδείας". Σαν να μην ήταν...
Και για το δεύτερο ερώτημά σου, πάντως, προφανής είναι η απάντηση και είναι και εδώ αρνητική ευτυχώς.

nPb · 20-12-10

To LaTex πού μπορώ να το βρω; Επίσης υπάρχει μάνιουαλ γραφής κειμένου και μαθηματικών στα ελληνικά;

Γιώργος · 20-12-10

Αρχική Δημοσίευση από nPb:
To LaTex πού μπορώ να το βρω;

$ apt-get install textlive

Και έπειτα βάζεις και κάποιο plugin για text editor, πχ:
$ sudo apt-get install gedit-latex-plugin

Απλό δεν είναι;

Dias · 20-12-10

Πιστεύω ότι το καλύτερο πρόγραμμα για να γράφει κάποιος μαθηματικά, φυσική, χημεία είναι το MathType (πρόσθετο του Office). Έχει άπειρες δυνατότητες και μπορείς συγχρόνως να γράφεις και κείμενο και στα Ελληνικά (καμμία σχέση με το lastex). Άλλη λύση πιο απλή είναι το word που έχει την επιλογή "εξίσωση". Μόνο που με αυτά που γράφω δεν μπορείς να τα κάνεις κατευθείαν paste εδώ στο φόρουμ. Αλλά αυτό λύνεται με μακροεντολή που σε χρόνο dt στο κάνει εικόνα, το ανεβάζει κάπου που έχεις λογαριασμό για φωτογραφίες και το επικολλάς εδώ.

hraklis123 · 24-12-10

Γειά σας!!Θα ήθελα να ρωτήσω αν τα θέματα που έχει ο Μπάρλας min max πιθανότητας ενός ενδεχομένου είναι μέσα στην ύλη.
Ευχαριστώ!

koum · 24-12-10

Αρχική Δημοσίευση από hraklis123:
Γειά σας!!Θα ήθελα να ρωτήσω αν τα θέματα που έχει ο Μπάρλας min max πιθανότητας ενός ενδεχομένου είναι μέσα στην ύλη.
Ευχαριστώ!

Ναι, είναι εντός.

13diagoras · 26-12-10

Αρχική Δημοσίευση από koum:
2) Σε σχολικά πλαίσια απαγορεύεται να θεωρήσεις $\alpha , \beta , \gamma$ μη πραγματικούς και να προχωρήσεις κανονικά στην εύρεση της Διακρίνουσας. Αν το δεις αυτό σε κάποιο βιβλίο, όχι απαραίτητα μόνο στο σχολικό, ειδοποίησέ με. Γι' αυτό και λέω ότι η λύση σου έχει κενό.

3)

Σε κάθε δευτεροβάθμια εξίσωση της μορφής $\alpha x^2+ \beta x + \gamma=0$ $,\alpha , \beta , \gamma \in R$ $, \alpha \neq 0$ , οι ρίζες της είναι πάντα 2 σε αριθμό. Δύο πραγματικές αλλά άνισες $(\Delta>0 )$ , διπλή πραγματική $(\Delta=0 )$ και δύο συζυγείς μιγαδικές $(\Delta<0 )$ .

Στην προκειμένη αναζητούμε τουλάχιστον μία ρίζα της εξίσωσης, ώστε να αληθεύει. Είναι γνωστό ότι τέτοια εξίσωση παριστάνει μια ευθεία (της μορφής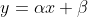 $y=\alpha x +\beta$ $, \alpha \neq 0 )$ . Οπότε στη προκειμένη, απαιτούμε ο συντελεστής του μεγιστοβάθμιου όρου να μηδενιστεί.

Για $\alpha =0$ , προκύπτει ο μιγαδικός ${z}_{1}=\frac{1}{2}-\frac{3}{2}i$ , ο οποίος είναι και ο ζητούμενος.

Συγνωμη που παρεμβαινω ,αν και λιγο καθηστερημενα.
Δεν καταλαβα πως, απο την στιγμη που ζηταει μια τουλαχιστον ριζα εμεις, απαιτουμε να εχει ακριβως μια.
Παντως η ασκηση εχει τα χαλια της...

nicksan · 12-01-11

παιδια μπορειτε να μου πειτε, αν υπαρχει, ενα αθροισμα πρωτων αριθμων που να ισουτε με 2011?
(περα απο το αθροισμα των 11 πρωτων και των 3)
επισης δεν με ενδιαφερει αν οι αριθμοι ειναι διαδοχικοι ή οχι

ευχαριστω εκ των προτερων

Dias · 13-01-11

Αρχική Δημοσίευση από nicksan:
παιδια μπορειτε να μου πειτε, αν υπαρχει, ενα αθροισμα πρωτων αριθμων που να ισουται με 2011?

1867 + 113 + 31 = 2011 . Σου κάνουν?

Di-tis · 14-01-11

Αρχική Δημοσίευση από alchemia:
Παιδια καλησπερα. Δεν ξερω αν εχει ξαναγινει η ερωτηση αλλα θα ρωτησω
Στα μαθηματικα γενικης μπορω να χρησιμοποιησω την εξισωση της εφ/νης y - f(xo) = f' (xo)(x-xo) ή πρεπει να παω κλασικα με την y=ax+b ;
Στο φροντιστηριο ειχαν πει οτι μπορουμε κανονικα ενω αυτος στο σχολειο ειπε οτι ειναι λαθος

καλησπέρα, στο σχολείο έμενα ο καθηγητής μου είπε τα εξής ( και κατα τη γνώμη μου έχει απόλυτο δίκιο):
Μας είπε οτι όσο καιρό διορθώνει στον Πειραιά δέν του έχει τύχει κανένας βαθμολογητής να κόψει βαθμούς για αυτό το λόγο, αλλα όταν ήταν στην επαρχία είχε συμβεί ένα περιστατικό στο οποίο ένας μαθητής είχε γράψει την εξίσωση εφαπτομένης στην γενική "y - f(xo) = f' (xo)(x-xo)" (οπως την κατεύθυνση) και του το έπιασαν λάθος.Τελικώς μας είπε για να έχετε το κεφάλι σας ήσυχο γράψτε την "y=αχ + β" γιατί όλοι ξέρουμε πώς δέν ξέρεις απο ποιόν διορθώνεσε και τι σκοτούρες έχει εκείνη την ώρα(δυστηχώς έτσι είναι) και αν σε αδικήσει μπορεί και να την πατήσεις και να πάει στράφι μια χρονιά...Οπότε μήν πάς κόντρα στο ρεύμα τους κατα τη γνώμη μου, και μετά μόλις βγούμε όλοι μας απο αυτό το λούκι τα ξεχνάμε...

Καλή Επιτυχία σε όλους μας παιδιά!

^EctiMel^ · 21-01-11

Παιδιά χρειάζομαι οπωσδήποτε μια μικρή βοήθεια με τα μαθηματικά γενικης

Λοιπόν: Ασκηση Β6 σελ 47
Ενα συρμα μηκους λ κόβεται σε δυο τμηματα με τα οποια σχηματιζουμε ενα τετραγωνο και ένα κυκλο αντιστοιχως. Να δείξετε ότι το άθροισμα των εμβαδών των δύο σχημάτων είναι ελάχιστο όταν η πλευρά του τετραγώνου είναι ίση με τη διάμετρο του κύκλου

Παραθέτω και την λύση και μετά θα αναφέρω που θέλω βοηθεια

Σαν σχήμα έχουμε το εξής

/--------------χ-----------/---------λ-χ-------/
/---------------------λ-------------------------/

Τώρα έστω χ το μηκος του κυκλου, τότε χ-λ είναι η περίμετρος του τετραγώνου. Αν ρ η ακτίνα του κύκου με μήκος χ τότε 2πρ=χ => ρ=χ/2π και το εμβαδό ειναι πρ^2=χ^2 / 4π
επειδή το τετράγωνο έχει περίμετρο α=λ-χ/4 και το εμβαδόν του είναι (λ-χ/4)^2
Καταληγουμε οτι το αθροισμα των εμβαδων ειναι Ε(χ)= χ^2/4π + (λ-χ/4)^2
Παραγωγίζοντας καταληγουμε Ε'(χ)=1/2π * χ - (λ-χ/8 ) και Ε΄΄(χ)>0
Μηδενίζουμε τη Ε΄(Χ) και παίρνουμε χ=λπ/4+π ως ρίζα.... Κάνοντας το ''πινακάκι'' βρίσκουμε'' οτι απο μειον απειρο εως την ρίζα η συναρτηση ειναι φθινουσα και απο την ρίζα έως το συν απειρο αυξουσα οποτε το χ=λπ/4+π είναι ελάχιστο οπότε για αυτό το χ έχουμε το ελάχιστο εμβαδόν... Όταν όμως χ=λπ/4+π η διάμετρος του κύκλου είναι δ=2ρ=2/2π * λπ/4+π=λ/4+π και η πλευρα του τετραγωνου ειναι επισης α=λ-χ/4 και για χ=λπ/4+π => α=λ/4+π

Εδω τελειωνει η ασκηση... Όμως θέλω το εξής... Για ποια τιμή του χ το άθροισμα των εμβαδών των 2 σχημάτων γίνεται μέγιστο?? είναι λιγάκι επειγον :redface:

rebel · 21-01-11

Αν μία συνάρτηση είναι ορισμένη και παραγωγίσιμη σε ένα κλειστό διάστημα τότε οι πιθανές θέσεις ολικού μεγίστου είναι τα σημεία μηδενισμού της παραγώγου, και τα άκρα του διαστήματος. Εδώ $x\in [0,\lambda]$ , οπότε $E(0)=\frac{\lambda^2}{16} \ E(\lambda)=\frac{\lambda^2}{8}$ . Άρα παρουσιάζει μέγιστο για $x=\lambda$ . Ελπίζω να μην έκανα κάποιο αριθμητικό λάθος

^EctiMel^ · 21-01-11

Ευχαριστώ πάρα πολύ

Τελικά την έλυσα και μόνος μου αλλά έκανα μια κάπως πιο γραφική λύση

Και εγώ τα ίδια αποτελέσματα έβγαλα μια χαρα

Antonis.1821 · 27 Ιανουαρίου 2011

Αρχική Δημοσίευση από koum:
2) Σε σχολικά πλαίσια απαγορεύεται να θεωρήσεις $\alpha , \beta , \gamma$ μη πραγματικούς και να προχωρήσεις κανονικά στην εύρεση της Διακρίνουσας. Αν το δεις αυτό σε κάποιο βιβλίο, όχι απαραίτητα μόνο στο σχολικό, ειδοποίησέ με.

Κι όμως: Ο τύπος ισχύει μια χαρά, και όταν οι συντελεστές είναι μιγαδικοί. Όμως ΔΕΝ είναι στην ύλη της Γ' Λυκείου. Και προφανώς δεν μπορείς να μιλήσεις για θετική/αρνητική Δ, αλλά δουλεύεις με απλές ισότητες. Δηλ. δεν βρίσκεις τετρ. ρίζα της -μιγαδικής- Δ, αλλά έναν μιγαδικό, ο οποίος στο τετράγωνο δίνει τη Δ...

Αρχική Δημοσίευση από Di-tis:
Τελικώς μας είπε για να έχετε το κεφάλι σας ήσυχο γράψτε την "y=αχ + β" γιατί όλοι ξέρουμε πώς δέν ξέρεις απο ποιόν διορθώνεσε και τι σκοτούρες έχει εκείνη την ώρα(δυστηχώς έτσι είναι) και αν σε αδικήσει μπορεί και να την πατήσεις και να πάει στράφι μια χρονιά...

Τα παραλές, αλλά... δεν θα διαφωνήσω μαζί σου. Η πιθανότητα να σου κόψει μονάδες κάποιος συνάδελφος σ' αυτή την περίπτωση, είναι μικρότερη από {e}^{-2011}, αλλά παντού υπάρχουν μαλ... . Επειδή διορθώνω κάτι χρόνια, ξέρω ότι τέτοια θέματα συζητούνται εκτενώς πριν αρχίσουμε τη βαθμολόγηση. Και πάντα θεωρούμε δεκτές τέτοιες λύσεις (εννοώ στα μαθημ. γεν. παιδ. να χρησιμοποιήσει κάποιος ύλη κατ/σης). Αλλά, όπως είπα (και λες κι εσύ), φύλαγε τα ρούχα σου, να έχεις τα μισά.

athinouli · 27-01-11

είναι γελοίο μάλλον που πάω τεχνολογική και δε ξέρω να λύνω το παρακάτω αλλά κόλλησα.. :/
α^2 + β^2 + γ^2 = 217
α + β + γ = 25
να βρώ τα α,β,γ..

βοήθεια παρακαλώ..

Dias · 27-01-11

Αρχική Δημοσίευση από athinouli:
α² + β² + γ² = 217
α + β + γ = 25
να βρώ τα α,β,γ... .

Σαν σύστημα δεν λύνεται γιατί έχει 2 εξισώσεις και 3 αγνώστους.
Αν θέλεις οι α, β, γ να είναι θετικοί ακέραιοι, τότε λύνεται σαν μαθηματικός γρίφος και η λύση είναι: 10, 9, 6
(Αν θέλεις σου λέω και πώς το βρήκα).

Και έλεος με αυτά τα χ^2!!! χ² γράφει ο κόσμος!!!
Δες πως βγαίνουν σύμβολα κατευθείαν από (ελληνικό) πληκτρολόγιο:
Δυνάμεις: ² : {CTRL ALT 2}, ³ : {CTRL ALT 3}, Μοίρες: ° : {CTRL ALT 0},
± : {CTRL ALT -}, ½ : {CTRL ALT +}, Απόλυτη τιμή: | :{SHIFT \}
Επίσης στο προφίλ μου (μηνύματα επισκεπτών) θα βρεις και πολλά άλλα σύμβολα για να τα κάνεις copy-paste.

rebel · 28-01-11

Αρχική Δημοσίευση από Dias:
Σαν σύστημα δεν λύνεται γιατί έχει 2 εξισώσεις και 3 αγνώστους.
Αν θέλεις οι α, β, γ να είναι θετικοί ακέραιοι, τότε λύνεται σαν μαθηματικός γρίφος και η λύση είναι: 10, 9, 6
(Αν θέλεις σου λέω και πώς το βρήκα).

Πως το βρήκες; :hmm:

athinouli · 28-01-11

πφφ.. πάλι καντήλια θα ακούσω σήμερα.. ίσως να μην αξιοποίησα σωστά τα δεδομένα της άσκησης έτσι ώστε να έβγαζα και άλλη εξίσωση..
εντάξει μη δαγκώνεις.. απλώς γράφω σε γλώσσα ανάπτυξης εφαρμογών

anyway υγεία..

Dias · 28-01-11

Αρχική Δημοσίευση από styt_geia:
Πως το βρήκες;

Απλό είναι. Όμως δεν είναι εξισώσεις κλπ, αλλά κάτι σαν γρίφος. Λοιπόν:
Τα τετράγωνα των ακεραίων μπορούν να τελειώνουν μόνον σε 0, 1, 4, 5, 6, 9.
Οι αριθμοί μας είναι < 15 (γιατί 15² = 225 > 217)
Στους αριθμους 1, 2, 3, 4, 5, 6, 7 ,8 ,9 ,10 ,11 ,12 ,13 ,14
τα τετράγωνα τελειώνουν αντίστοιχα σε:
1, 4, 9, 6, 5, 6, 9, 4, 1, 0, 1, 4, 9, 6
Άθροισμα τετραγώνων που τελειώνει σε 7 μπορούν να δώσουν μόνον αυτοί οι 3 που τα τετράγωνα τους τελειώνουν σε:
9+9+9 : (Π.χ. 3+3+3, 3+3+7, 3+7+7, 7+7+7, 3+3+13, 3+7+13 κλπ, όλα ≠ 25)
1+1+5 : (Π.χ. 1+9+5, 1+11+5, κλπ ≠ 25, όμως 9+11+5 = 25 αλλά 9²+11²+5²≠217)
0+1+6 : (Π.χ. 10+9+4≠25, 10+11+4 = 25 αλλά 10²+11²+4²≠217),
όμως: 6+9+10 = 25 και 6²+9²+10² = 217, άρα βρέθηκαν: 6, 9, 10.
Δεν ξέρω μήπως υπάρχει και άλλη τριάδα και μου ξέφυγε. Ίσως τώρα που έγραψα πώς σκέφτηκα, να φανεί σε κάποιον πολύπλοκο, αλλά με το μυαλό μου ήρθε αμέσως η λύση. :redface:

Αρχική Δημοσίευση από athinouli:
γράφω σε γλώσσα ανάπτυξης εφαρμογών

Δεν κάνω ΑΕΠΠ και δεν ξέρω την ψευτογλώσσα σας, όμως επειδή ξέρω λίγο basic, νομίζω ότι ένα απλό προγραμματάκι που διαβάζει τριάδες αριθμών και βρίσκει άθροισμα και άθροισμα τετραγώνων και τα συγκρίνει με τα δοσμένα, είναι πολύ απλό.

skiouroosasdf · 30-01-11

Ξερει κανεις πως υπολογίζεται το lim(x-> -∞) { ln(x^2+1) + x } ;

Βοήθεια/Απορίες στα Μαθηματικά Γενικής Παιδείας

Διάσημο μέλος

Επιφανές μέλος

Τιμώμενο Μέλος

Επιφανές μέλος

Νεοφερμένος

Πολύ δραστήριο μέλος

Δραστήριο μέλος

Νεοφερμένος

Επιφανές μέλος

Νεοφερμένος

Νεοφερμένος

Πολύ δραστήριο μέλος

Νεοφερμένος

Νεοφερμένος

Εκκολαπτόμενο μέλος

Επιφανές μέλος

Πολύ δραστήριο μέλος

Εκκολαπτόμενο μέλος

Επιφανές μέλος

Νεοφερμένος