

Οπότε λαμβάνουμε τις σχέσεις:
-2χ + 2z + 3y - 3w = -3 (1)
2x + 4z - 3y - 6w = -9 (2)
x - z - 2y + 2w = 2 (3)
-x - 2z + 2y + 4w = 7 (4)
Με προσθήκη κατά μέλη των (1) και (2) λαμβάνουμε την σχέση
2z - 3w = -4 (5).
x - z - 2y + 2w = 2 =>
2x - 2z - 4y + 4w = 4 (6)
Με προσθήκη των (1) και (6) παίρνουμε
w - y = 1 (7)
Με προσθήκη των (3) και (4) παίρνουμε ότι 6w - 3z = 9 => 2w - z = 3 =>
4w - 2z = 6 (8)
Με προσθήκη των (5) και (8) παίρνουμε ότι
w = 2, και από την (7) ότι
y = 1. Αντίστοιχα από την (5),
z = 1. Τελικά μένει μόνο ο άγνωστος x, για τον οποίο ισχύει χ - 1 - 2 + 4 = 2 =>
χ = 1.
Άρα για τις τιμές (χ, y, z, w) ισχύει οπωσδήποτε (x, y, z, w) = (1, 1, 1, 2), και άρα ο μοναδικός πίνακας Z που επαληθεύει την σχέση είναι ο:

Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.


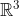 πρέπει να δείξεις δύο πράγματα
πρέπει να δείξεις δύο πράγματα) και
και ) στοιχεία του συνόλου
στοιχεία του συνόλου 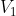 τότε και το άθροισμά τους
τότε και το άθροισμά τους ) είναι στοιχείο του
είναι στοιχείο του 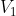
) στοιχείο του
στοιχείο του 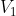 και
και 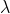 πραγματικός αριθμός, τότε
πραγματικός αριθμός, τότε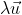 είναι στοιχείο του
είναι στοιχείο του 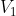
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki

 και το βρισκω λογικό αφού δεν ισχύει η αντιμεταθετική ιδιότητα. thanks!
και το βρισκω λογικό αφού δεν ισχύει η αντιμεταθετική ιδιότητα. thanks!

