Dias
Επιφανές μέλος
Ο Dias αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Καθηγητής κι έχει σπουδάσει στο τμήμα Φυσικής ΕΚΠΑ (Αθήνα). Έχει γράψει 10.315 μηνύματα.

22-12-23

12:58

Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 26 ετών, Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11.425 μηνύματα.

22-12-23

18:53
Πρόβλημα :
Μια χιονόμπαλα ακτίνας ro και μάζας mο ξεκινάει απο ηρεμία να κυλάει στην κατακόρυφη πλευρά ενός λόφου ύψους h υπό την επίδραση της βαρύτητας. Καθώς η χιονόμπαλα κυλίεται στην κατακόρυφη πλευρά του λόφου το μέγεθος της αυξάνεται λόγω της συλλογής χιονιού απο το έδαφος. Στο κάτω μέρος του λόφου υπάρχει δρόμος.
α) Να μελετηθεί η κίνηση της χιονόμπαλας συναρτήσει του χρόνου εαν γίνει η υπόθεση οτι η ακτίνα αυξάνεται κατά σταθερό ποσό ίσο με C ανά περιστροφή της χιονόμπαλας.
β) Να βρεθεί η τελική μάζα της χιονόμπαλας όταν φτάσει στον δρόμο.
γ) Πόσο χρόνο θα χρειαστεί η χιονόμπαλα για να φτάσει στον δρόμο ;
δ) Ποια θα είναι η συνολική κινητική ενέργεια της όταν φτάσει στον δρόμο ;
ε) Επαναλάβετε τα προηγούμενα για την περίπτωση που η πλευρά του λόφου σχηματίζει γωνία θ με το επίπεδο του δρόμου.
ζ) Επαναλάβετε τα προηγούμενα εαν αντί για σφαίρα χρησιμοποιηθεί κορμός δέντρου μήκους L και καταγράψτε τις όποιες παρατηρήσεις σας.
Δίνεται η ροπή αδράνειας και ο όγκος σφαίρας και κυλίνδρου ως :
Iσ = (⅖)mr²
Vσ = (4/3)πr³
Ικ = (1/2)mr²
Μια χιονόμπαλα ακτίνας ro και μάζας mο ξεκινάει απο ηρεμία να κυλάει στην κατακόρυφη πλευρά ενός λόφου ύψους h υπό την επίδραση της βαρύτητας. Καθώς η χιονόμπαλα κυλίεται στην κατακόρυφη πλευρά του λόφου το μέγεθος της αυξάνεται λόγω της συλλογής χιονιού απο το έδαφος. Στο κάτω μέρος του λόφου υπάρχει δρόμος.
α) Να μελετηθεί η κίνηση της χιονόμπαλας συναρτήσει του χρόνου εαν γίνει η υπόθεση οτι η ακτίνα αυξάνεται κατά σταθερό ποσό ίσο με C ανά περιστροφή της χιονόμπαλας.
β) Να βρεθεί η τελική μάζα της χιονόμπαλας όταν φτάσει στον δρόμο.
γ) Πόσο χρόνο θα χρειαστεί η χιονόμπαλα για να φτάσει στον δρόμο ;
δ) Ποια θα είναι η συνολική κινητική ενέργεια της όταν φτάσει στον δρόμο ;
ε) Επαναλάβετε τα προηγούμενα για την περίπτωση που η πλευρά του λόφου σχηματίζει γωνία θ με το επίπεδο του δρόμου.
ζ) Επαναλάβετε τα προηγούμενα εαν αντί για σφαίρα χρησιμοποιηθεί κορμός δέντρου μήκους L και καταγράψτε τις όποιες παρατηρήσεις σας.
Δίνεται η ροπή αδράνειας και ο όγκος σφαίρας και κυλίνδρου ως :
Iσ = (⅖)mr²
Vσ = (4/3)πr³
Ικ = (1/2)mr²
Dias
Επιφανές μέλος
Ο Dias αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Καθηγητής κι έχει σπουδάσει στο τμήμα Φυσικής ΕΚΠΑ (Αθήνα). Έχει γράψει 10.315 μηνύματα.

23-12-23

17:14

Dias
Επιφανές μέλος
Ο Dias αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Καθηγητής κι έχει σπουδάσει στο τμήμα Φυσικής ΕΚΠΑ (Αθήνα). Έχει γράψει 10.315 μηνύματα.

23-12-23

18:20
Περνάω κύριε;Πρόβλημα :
......................................................................................

Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 26 ετών, Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11.425 μηνύματα.

23-12-23

18:27
Πρέπει να χρησιμοποιήσεις τους νομούς του Νεύτωνα στην γενική τους μορφή, διότι μεταβάλλεται και η μάζα αλλά και η ροπή αδράνειας του σώματος ταυτόχρονα !
Dias
Επιφανές μέλος
Ο Dias αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Καθηγητής κι έχει σπουδάσει στο τμήμα Φυσικής ΕΚΠΑ (Αθήνα). Έχει γράψει 10.315 μηνύματα.

23-12-23

18:33
Το σκέφτηκα, αλλά απέδειξα για τυχαία στιγμή ότι η επιτάχυνση είναι ανεξάρτητη ακτίνας και μάζας και σταθερή. (Περιμένω τη δική σου λύση)Πρέπει να χρησιμοποιήσεις τους νομούς του Νεύτωνα στην γενική τους μορφή, διότι μεταβάλλεται και η μάζα αλλά και η ροπή αδράνειας του σώματος ταυτόχρονα !

Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 26 ετών, Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11.425 μηνύματα.

23-12-23

18:41
Μμ δεν είναι κακό, θα βοηθήσει αυτή η προσέγγιση στην καλύτερη αντίληψη του προβλήματος.Το σκέφτηκα, αλλά απέδειξα για τυχαία στιγμή ότι η επιτάχυνση είναι ανεξάρτητη ακτίνας και μάζας και σταθερή. (Περιμένω τη δική σου λύση)

Επειδή αυτή την στιγμή δεν προλαβαίνω γιατί πρέπει να φύγω, θα ανεβάσω την λύση αργότερα το βράδυ.
Dias
Επιφανές μέλος
Ο Dias αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Καθηγητής κι έχει σπουδάσει στο τμήμα Φυσικής ΕΚΠΑ (Αθήνα). Έχει γράψει 10.315 μηνύματα.

24-12-23

10:23

Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 26 ετών, Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11.425 μηνύματα.

25-12-23

13:45
Πάμε να το δούμε λίγο αυτό.Πρόβλημα :
Μια χιονόμπαλα ακτίνας ro και μάζας mο ξεκινάει απο ηρεμία να κυλάει στην κατακόρυφη πλευρά ενός λόφου ύψους h υπό την επίδραση της βαρύτητας. Καθώς η χιονόμπαλα κυλίεται στην κατακόρυφη πλευρά του λόφου το μέγεθος της αυξάνεται λόγω της συλλογής χιονιού απο το έδαφος. Στο κάτω μέρος του λόφου υπάρχει δρόμος.
α) Να μελετηθεί η κίνηση της χιονόμπαλας συναρτήσει του χρόνου εαν γίνει η υπόθεση οτι η ακτίνα αυξάνεται κατά σταθερό ποσό ίσο με C ανά περιστροφή της χιονόμπαλας.
β) Να βρεθεί η τελική μάζα της χιονόμπαλας όταν φτάσει στον δρόμο.
γ) Πόσο χρόνο θα χρειαστεί η χιονόμπαλα για να φτάσει στον δρόμο ;
δ) Ποια θα είναι η συνολική κινητική ενέργεια της όταν φτάσει στον δρόμο ;
ε) Επαναλάβετε τα προηγούμενα για την περίπτωση που η πλευρά του λόφου σχηματίζει γωνία θ με το επίπεδο του δρόμου.
ζ) Επαναλάβετε τα προηγούμενα εαν αντί για σφαίρα χρησιμοποιηθεί κορμός δέντρου μήκους L και καταγράψτε τις όποιες παρατηρήσεις σας.
Δίνεται η ροπή αδράνειας και ο όγκος σφαίρας και κυλίνδρου ως :
Iσ = (⅖)mr²
Vσ = (4/3)πr³
Ικ = (1/2)mr²
Η προσέγγιση απο την σκοπιά της θεωρίας :
pos_fig = figure;
radi_fig = figure;
vel_fig = figure;
accel_fig = figure;
for ro = 0.1:0.5:5
snowball_sim(ro, 100, 0.05, pos_fig, radi_fig, vel_fig, accel_fig)
end
function snowball_sim(ro, h, C, pos_fig, radi_fig, vel_fig, accel_fig)
% Set the constants
g = 9.81;
density = 600;
k1 = 30/7;
k2 = (5 * g * C) / (14 * pi); % Assuming g = 9.81 m/s^2
% Set the initial conditions
initial_conditions = [ro; 0];
% Set the time span for the solution
tspan = [0 30]; % Adjust the end time as needed
% Set the maximum step size
maxStep = 0.1; % Adjust this value as needed
% Solve the system of ODEs using ode45
options = odeset('MaxStep', maxStep);
[t, y] = ode45(@(t, y) myODE(t, y, k1, k2), tspan, initial_conditions, options);
% Extract the results
r_t = y(:, 1);
% Calculate y(t)
y_t = ((2 * pi) / C) * (r_t.^2 / 2 - ro^2 / 2);
% Calculate the velocity u(t)
u_t = ((2 * pi) / C) * r_t .* y(:, 2);
% Differentiate the velocity to get acceleration a(t)
a_t = diff(u_t) ./ diff(t);
% Plot individual figures
figure(pos_fig);
% Figure 1: Snowball's vertical position y
plot(t, y_t, 'LineWidth', 2);
xlabel('t(s)');
ylabel("y(t)");
title("Snowball's Vertical Position as a Function of Time");
grid on;
hold on;
figure(radi_fig);
% Figure 2: Snowball's Radius r
plot(t, r_t, 'LineWidth', 2);
xlabel('t(s)');
ylabel("r(t)");
title("Snowball's Radius as a Function of Time");
grid on;
hold on;
figure(vel_fig);
% Figure 3: Snowball's Velocity u
plot(t, u_t, 'LineWidth', 2);
xlabel('t(s)');
ylabel("u(t)");
title("Snowball's velocity as a Function of time");
grid on;
hold on;
figure(accel_fig);
% Snowball's acceleration a
plot(t(1:end-1), a_t, 'LineWidth', 2);
xlabel('t(s)');
ylabel('a(t)');
title("Snowball's Acceleration");
grid on;
hold on;
%Calculate time for snowball to hit road
indx = 1;
while r_t(indx) < sqrt((h*C)/pi + ro^2)
to = t(indx);
indx = indx+1;
end
disp("____________________________________________________")
disp("ro = "+ro +", C = " +C + ", h = " + h)
disp("____________________________________________________")
to
disp("----------------------------------------------------")
%Snowball's mass ratio
mass_ratio = (r_t(indx)/ro).^3
disp("----------------------------------------------------")
mass_final = (4/3)*pi*density*(r_t(indx))^3
disp("----------------------------------------------------")
%Snowball's total kinetic energy
K = (28*pi*density/15)*((r_t(indx))^3)*(u_t(indx))^2
% Define the function representing the system of ODEs
function dydt = myODE(t, y, k1, k2)
dydt = zeros(2, 1);
dydt(1) = y(2);
dydt(2) = (k2 - k1*y(2)^2) / y(1);
end
end
radi_fig = figure;
vel_fig = figure;
accel_fig = figure;
for ro = 0.1:0.5:5
snowball_sim(ro, 100, 0.05, pos_fig, radi_fig, vel_fig, accel_fig)
end
function snowball_sim(ro, h, C, pos_fig, radi_fig, vel_fig, accel_fig)
% Set the constants
g = 9.81;
density = 600;
k1 = 30/7;
k2 = (5 * g * C) / (14 * pi); % Assuming g = 9.81 m/s^2
% Set the initial conditions
initial_conditions = [ro; 0];
% Set the time span for the solution
tspan = [0 30]; % Adjust the end time as needed
% Set the maximum step size
maxStep = 0.1; % Adjust this value as needed
% Solve the system of ODEs using ode45
options = odeset('MaxStep', maxStep);
[t, y] = ode45(@(t, y) myODE(t, y, k1, k2), tspan, initial_conditions, options);
% Extract the results
r_t = y(:, 1);
% Calculate y(t)
y_t = ((2 * pi) / C) * (r_t.^2 / 2 - ro^2 / 2);
% Calculate the velocity u(t)
u_t = ((2 * pi) / C) * r_t .* y(:, 2);
% Differentiate the velocity to get acceleration a(t)
a_t = diff(u_t) ./ diff(t);
% Plot individual figures
figure(pos_fig);
% Figure 1: Snowball's vertical position y
plot(t, y_t, 'LineWidth', 2);
xlabel('t(s)');
ylabel("y(t)");
title("Snowball's Vertical Position as a Function of Time");
grid on;
hold on;
figure(radi_fig);
% Figure 2: Snowball's Radius r
plot(t, r_t, 'LineWidth', 2);
xlabel('t(s)');
ylabel("r(t)");
title("Snowball's Radius as a Function of Time");
grid on;
hold on;
figure(vel_fig);
% Figure 3: Snowball's Velocity u
plot(t, u_t, 'LineWidth', 2);
xlabel('t(s)');
ylabel("u(t)");
title("Snowball's velocity as a Function of time");
grid on;
hold on;
figure(accel_fig);
% Snowball's acceleration a
plot(t(1:end-1), a_t, 'LineWidth', 2);
xlabel('t(s)');
ylabel('a(t)');
title("Snowball's Acceleration");
grid on;
hold on;
%Calculate time for snowball to hit road
indx = 1;
while r_t(indx) < sqrt((h*C)/pi + ro^2)
to = t(indx);
indx = indx+1;
end
disp("____________________________________________________")
disp("ro = "+ro +", C = " +C + ", h = " + h)
disp("____________________________________________________")
to
disp("----------------------------------------------------")
%Snowball's mass ratio
mass_ratio = (r_t(indx)/ro).^3
disp("----------------------------------------------------")
mass_final = (4/3)*pi*density*(r_t(indx))^3
disp("----------------------------------------------------")
%Snowball's total kinetic energy
K = (28*pi*density/15)*((r_t(indx))^3)*(u_t(indx))^2
% Define the function representing the system of ODEs
function dydt = myODE(t, y, k1, k2)
dydt = zeros(2, 1);
dydt(1) = y(2);
dydt(2) = (k2 - k1*y(2)^2) / y(1);
end
end
Η λογική είναι ίδια και για τον κορμό δέντρου, το μόνο που αλλάζει επί της ουσίας είναι ο όγκος, και η ροπή αδράνειας.
- Ενδιαφέρον παρουσιάζει το γεγονός οτι η ακτίνα της χιονόμπαλας για μικρές αρχικές ακτίνες είναι σχεδόν γραμμική συνάρτηση του χρόνου, ενώ για μεγαλύτερες όπως 2m και άνω ας πούμε, παρατηρείται μια έντονη μη γραμμικότητα εως και τα πρώτα 5 δευτερόλεπτα περίπου.
- Το αμέσως επόμενο αξιοσημείωτο είναι οτι η αρχική επιτάχυνση δεν επηρεάζεται απο την αρχική ακτίνα της χιονόμπαλας και είναι 5g/7, το οποίο ισούται περίπου με 7 m/s², και έχει δείξει ο @Dias αναλυτικά πως προκύπτει. Επίσης αξιοσημείωτο είναι οτι μετά απο διάστημα που εξαρτάται απο την αρχική ακτίνα της χιονόμπαλας, η επιτάχυνση σταθεροποιείται σε μια ορισμένη τιμή η οποία ωστόσο φαίνεται οτι είναι ανεξάρτητη απο την αρχική ακτίνα της χιονόμπαλας.
- Παρατηρούμε επίσης οτι οι χιονόμπαλες με την μικρότερη αρχική ακτίνα έχουν πιο γραμμική σχέση ταχύτητας σε σχέση με τον χρόνο ή ισοδύναμα απαιτείται περισσότερο χρόνος μέχρι να σταθεροποιηθεί η επιτάχυνση τους. Επιπλέον αυτές οι χιονόμπαλες χρειάζονται και περισσότερο χρόνο για να διανύσουν ορισμένη απόσταση σε σχέση με πιο μεγάλες.
- Ενδιαφέρον συμπεράσματα εξάγουμε και απο την μεταβολή του C που είναι ένα μέτρο του πόσο γρήγορα "συλλέγει" χιόνι απο το έδαφος η χιονόμπαλα. Παρατηρούμε οτι αυτές που έχουν μικρό συντελεστή C έχουν πιο αργή μεταβολή της ακτίνας τους, το οποίο είναι και λογικό και αναμενόμενο. Απο την άλλη, αυτές με μικρό συντελεστή C αναπτύσουν μεγαλύτερες ταχύτητες απο άλλες με μεγαλύτερο συντελεστή C και επομένως διανύουν δεδομένο δίαστημα πιο γρήγορα. Αυτό δεν πρέπει να προβληματίζει καθώς στο όριο που το C τείνει στο 0, η ακτίνα μεταβάλλεται τόσο αργά που μπορούμε να την θεωρήσουμε σχεδόν σταθερή. Μια τέτοια χιονόμπαλα σαφώς θα κινείται πιο γρήγορα καθώς εδώ δεν υπάρχει ο μηχανισμός προσθήκης μάζας. Οι δυνάμεις που ασκούνται δεν αλλάζουν μεταξύ των δύο περιπτώσεων, αλλά μέρος της συνισταμένη αφορά πλέον πέρα απο μια επιτάχυνση και έναν θετικό ρυθμό μεταβολής μάζας, ενώ επιπλέον και η ίδια η μάζα στον όρο mα αυξάνεται, οπότε αυτό μειώνει την αντίστοιχη επιτάχυνση. Τα όσα παρατηρούμε ερμηνεύονται λοιπόν με πολύ ικανοποιητικό τρόπο.
Dias
Επιφανές μέλος
Ο Dias αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Καθηγητής κι έχει σπουδάσει στο τμήμα Φυσικής ΕΚΠΑ (Αθήνα). Έχει γράψει 10.315 μηνύματα.

25-12-23

16:57
Tι θα λέγατε για κάτι σχετικό με τη σημερινή μέρα;

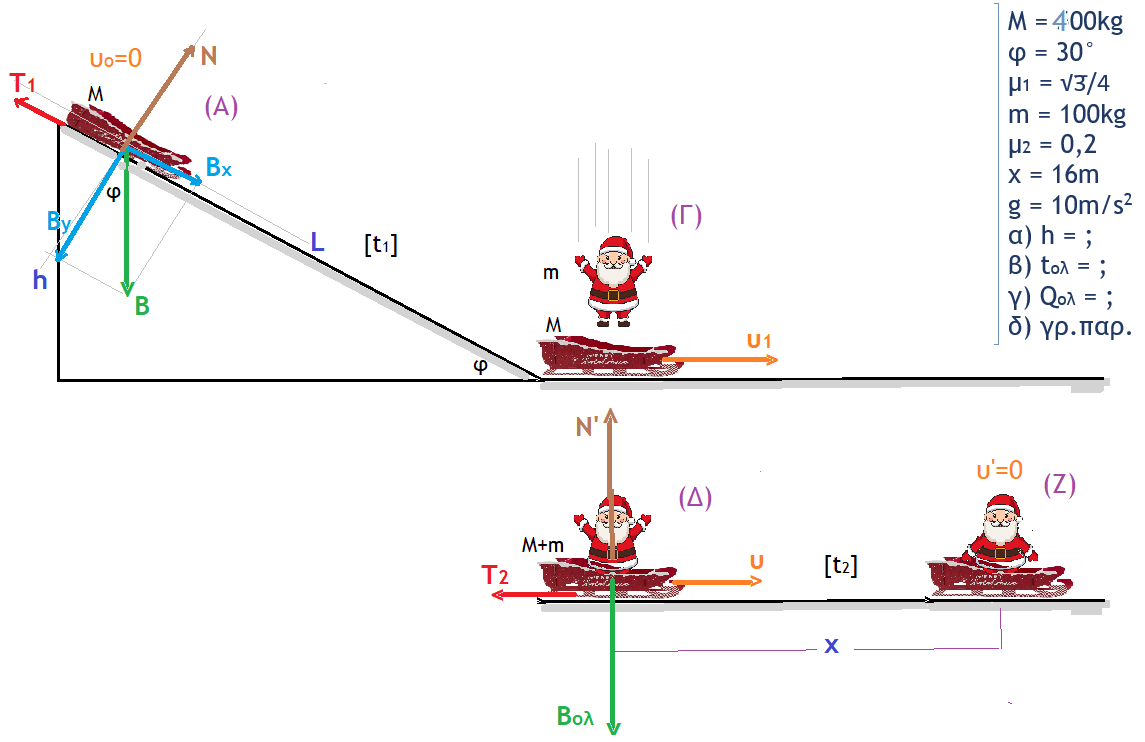

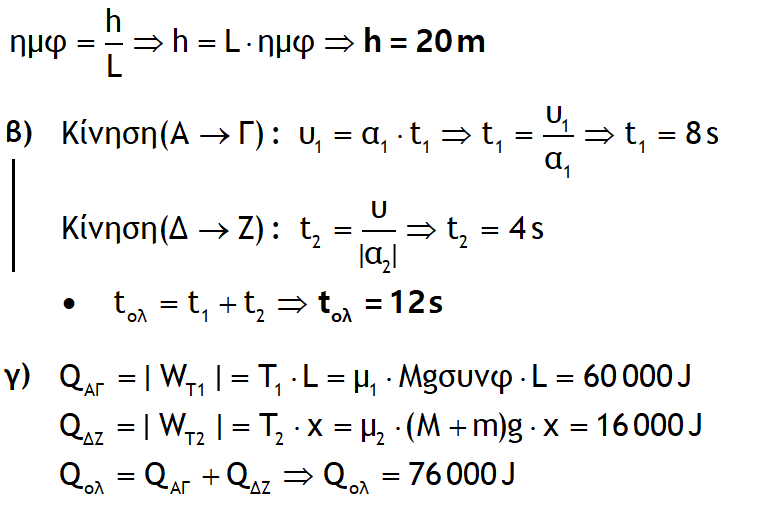
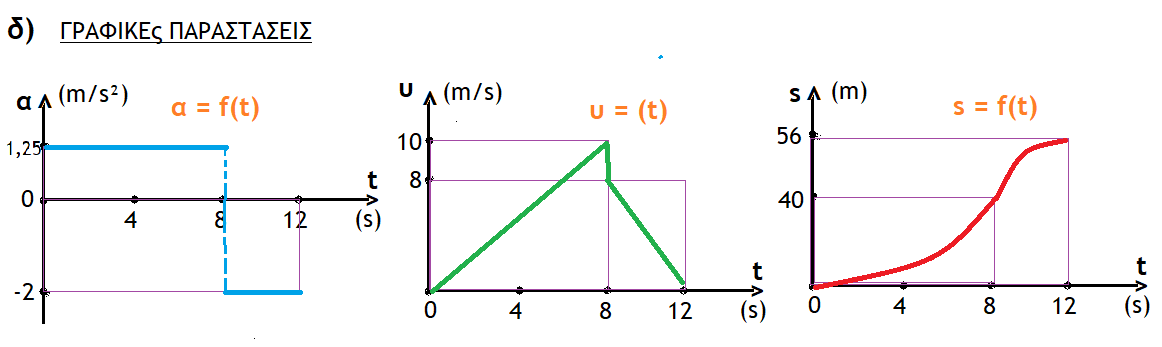 ΧΟ - ΧΟ - ΧΟ ΧΡΟΝΙΑ ΠΟΛ²Α ΣΕ ΟΛΟΥΣ
ΧΟ - ΧΟ - ΧΟ ΧΡΟΝΙΑ ΠΟΛ²Α ΣΕ ΟΛΟΥΣ


nearos
Επιφανές μέλος
Ο Giorgos αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 18 ετών και Μαθητής Γ' λυκείου. Έχει γράψει 9.533 μηνύματα.

25-12-23

17:12
εγραψες διααα
Dias
Επιφανές μέλος
Ο Dias αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Καθηγητής κι έχει σπουδάσει στο τμήμα Φυσικής ΕΚΠΑ (Αθήνα). Έχει γράψει 10.315 μηνύματα.

26-12-23

16:23

Cade
Πολύ δραστήριο μέλος
Ο Cade αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Απόφοιτος λυκείου. Έχει γράψει 856 μηνύματα.

26-12-23

17:16
Μηχανική παραμορφώσιμου στερεού #3 :
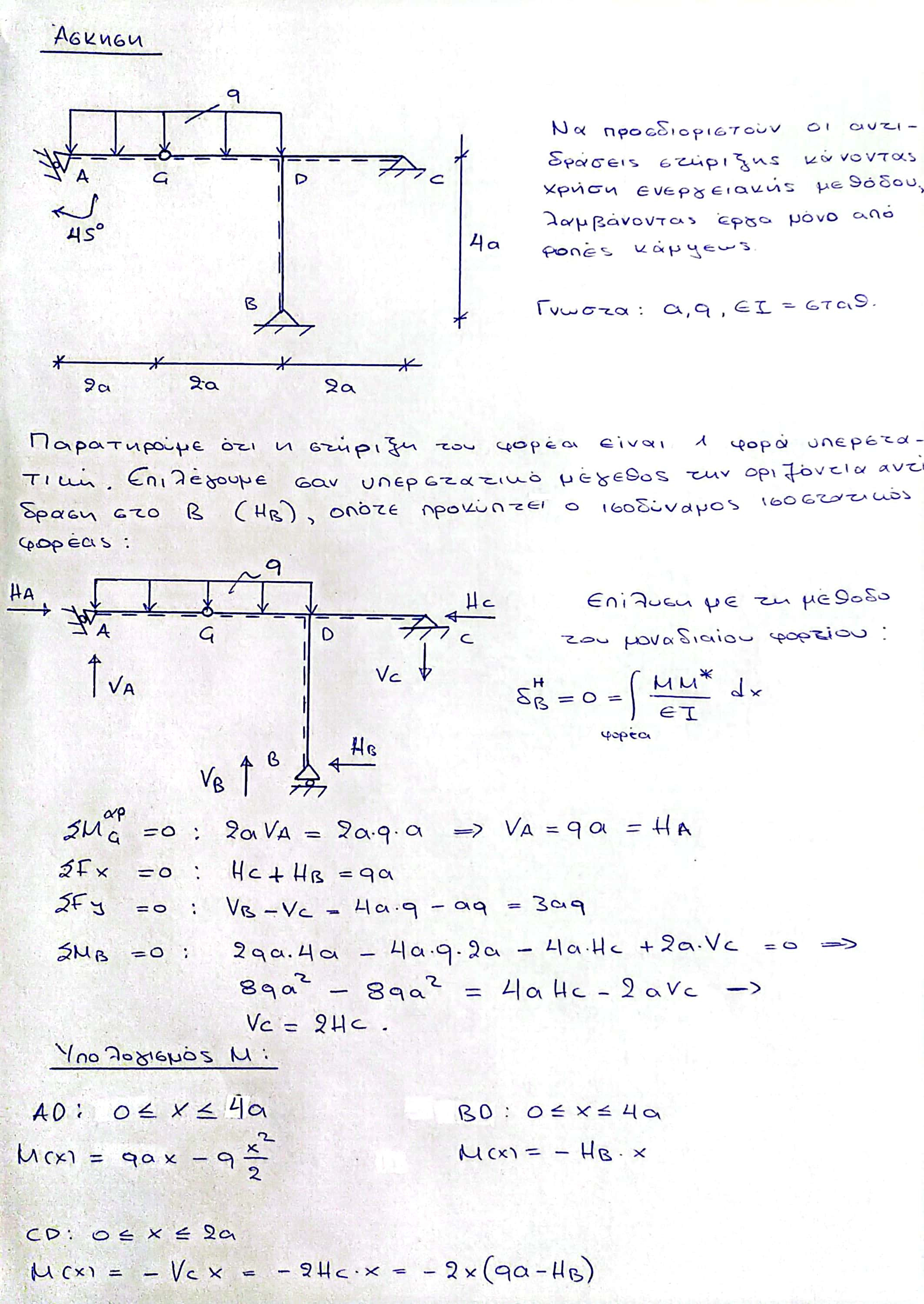

Dias
Επιφανές μέλος
Ο Dias αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Καθηγητής κι έχει σπουδάσει στο τμήμα Φυσικής ΕΚΠΑ (Αθήνα). Έχει γράψει 10.315 μηνύματα.

27-12-23

12:10

nearos
Επιφανές μέλος
Ο Giorgos αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 18 ετών και Μαθητής Γ' λυκείου. Έχει γράψει 9.533 μηνύματα.

27-12-23

16:59
Δία, τις ζωγραφιές, τις κανεις στο MS Paint? Με φοβίζουν αυτά τα κόκκινα τριγωνάκια στο κύμα.. Εχεις ελευθερο χρονο ε; 

Dias
Επιφανές μέλος
Ο Dias αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Καθηγητής κι έχει σπουδάσει στο τμήμα Φυσικής ΕΚΠΑ (Αθήνα). Έχει γράψει 10.315 μηνύματα.

28-12-23

17:07
1) Μπα! Οι ζωγραφιές μου δεν είναι δύσκολες, ούτε χρειάζονται πολύ χρόνο να γίνουν (άμα είσαι εξασκημένος).Δία, τις ζωγραφιές, τις κανεις στο MS Paint? Με φοβίζουν αυτά τα κόκκινα τριγωνάκια στο κύμα.. Εχεις ελευθερο χρονο ε;
2) Μη νομίζεις ότι τώρα γράφω τις ασκήσεις. Τις ανεβάζω από το προσωπικό μου αρχείο που το ξεκίνησα όταν ήμουν ακόμα μαθητής.
3) Δουλεύω αρκετές ώρες, οπότε κανένας δεν μπορεί να με κατηγορήσει ότι έχω ελεύθερο χρόνο.

Dias
Επιφανές μέλος
Ο Dias αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Καθηγητής κι έχει σπουδάσει στο τμήμα Φυσικής ΕΚΠΑ (Αθήνα). Έχει γράψει 10.315 μηνύματα.

28-12-23

19:24

Dias
Επιφανές μέλος
Ο Dias αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Καθηγητής κι έχει σπουδάσει στο τμήμα Φυσικής ΕΚΠΑ (Αθήνα). Έχει γράψει 10.315 μηνύματα.

29-12-23

12:47

ultraviolence
Τιμώμενο Μέλος
Ο ultraviolence αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος και μας γράφει από Γαλλία (Ευρώπη). Έχει γράψει 15.285 μηνύματα.

29-12-23

18:08
Καλησπέρα, έχω μια ερώτηση μιας κι σας βλέπω ορεξάτους γενικά : Παίζουν πουθενά στο ίντερνετ καλές σημειώσεις/slides για ΦΥΣΙΚΗ Ι που να σας βοήθησαν; ( ύλη = τα κλασικά κεφάλαια που έχουν τα εισαγωγικά μαθήματα φυσικής ). Ποτέ δεν χώνεψα τούτο το μάθημα και δεν χάνει την ευκαιρία να με γονατίζει. 
Ευχαριστώ κι σόρρυ αν είμαι οφφ!

Ευχαριστώ κι σόρρυ αν είμαι οφφ!
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 1 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 264 μέλη διάβασαν αυτό το θέμα:
- Chrisphys
- rseven
- Hased Babis
- Debugging_Demon
- tsiobieman
- Hecticism
- andromaxh07
- Unboxholics
- Corfu kitty
- jellojina
- Scandal
- bibliofagos
- Kate1914
- georgetherrr
- antonis97
- Reader
- BatGuin
- thesmilingchild
- iiTzArismaltor_
- Μήτσος10
- Orfano
- charmander
- panosT436
- eirinipap
- exotic xo
- Giorgosvr
- Qwerty 0
- Than003
- angela_k
- Jomo
- Joji
- pnf292
- kost28
- suaimhneas
- Greg25
- redpointer
- Albert.123
- Leo komm
- P.Dam.
- Steliosgkougkou
- chjan
- Evangeloz
- jYanniss
- love_to_learn
- wmaria
- Maynard
- χημεια4λαιφ
- donut_daddy
- marikakitsou16
- physicscrazy
- Lia 2006
- Wonderkid
- chester20080
- panaman
- Msp1
- Sotis
- mirara
- melver
- grad778
- nickd
- V@Per
- sakplat
- ssalex
- despoina13
- catlover033
- carnage
- Μιχαήλ
- eukleidhs1821
- vas2017
- beatrixx
- phleidhs
- gegeorgiou90
- Dr. Gl. Luminous
- agg41
- thepigod762
- Helen06
- Primary Care
- math2arch
- MrDragonboy
- chrismpd
- bill09876
- Paragontas7000
- ikigai
- Marel
- soleilst
- Startx0
- marilenaaa
- EllieKal
- gzois
- akis_95
- EFAKIT
- Φινεύς
- estrela
- Lifelong Learner
- Annie
- Panatha mono
- Mitsaras23
- Isa
- ggl
- BiteTheDust
- Chris180
- aplalew
- user111
- Chemwizard
- giannhs2001
- Mukumbura
- MR WHITE
- SIAmia
- supertom4000
- J.Cameron
- ougkampougka
- persour
- Totreno
- sotirislk
- Specon
- Mariosm.
- Claire05
- Giorgos216
- Jimpower
- shezza94
- kwstasloul
- kan3nas
- dmav
- Obi-Wan Kenobi
- Nancysmilkyway
- Νομάρχης
- ogigidi
- ένας τυχαίος
- Hmmytheos
- constansn
- cannot_log_in
- hello1234
- ilal1200
- Alessandra Eliza
- Giannis327
- phoni
- aggorf
- Nala
- Frozensun
- xrisamikol
- Ilovemycats27
- PanosApo
- nik64
- angies
- dimitris_eee
- mike19
- angeloskar
- eltqt
- CrusaderKingsIII
- flaura
- elevag
- Patroklos
- Anonymous1
- IcedBreaje
- kiyoshi
- nicole1982
- Lost_In_Life
- Γατέχων
- AggelikiGr
- Nansytsg
- Athens2002
- k4t
- Maria_Xagorari
- suuuuiiii
- SoyN
- thecrazycretan
- Jesse_
- A350
- Ιωάννης1234
- george777
- Abiogenesis
- Enhypen
- Mary06
- arko
- Giorgkalo
- velentzakoss
- Giota_pel
- AnnaRd
- Νικολινα
- NikNik1995
- BillyTheKid
- Nick_nt
- a namaves
- xristarac
- ilovekpop
- GeorgePap2003
- Sofos Gerontas
- topg
- Γιώτα Γιαννακού
- plantbee
- Peter Pan13
- Ness
- MrDna
- Jojo K
- Mewmaw
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki


