bovid19
Εκκολαπτόμενο μέλος
Ο bovid19 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 26 ετών και Πτυχιούχος του τμήματος Οικονομικής Επιστήμης ΟΠΑ. Έχει γράψει 343 μηνύματα.

05-04-21

15:01
Ας βάλω μια απλή:
Ρίχνουμε δύο ζάρια και θεωρούμε ως Χ τον μικρότερο αριθμό που προκύπτει μεταξύ των δύο. Να βρεθεί η σ.μ.π P(X=x) συναρτήσει του x.
Ρίχνουμε δύο ζάρια και θεωρούμε ως Χ τον μικρότερο αριθμό που προκύπτει μεταξύ των δύο. Να βρεθεί η σ.μ.π P(X=x) συναρτήσει του x.
Guest 190013
Επισκέπτης
αυτή τη στιγμή δεν είναι συνδεδεμέν. Δεν έχει γράψει κανένα μήνυμα.

05-04-21

19:19
Εξαντλητικά δε το προσδιορίζεις; Υπάρχει πιο συνοπτική επίλυση;Ρίχνουμε δύο ζάρια και θεωρούμε ως Χ τον μικρότερο αριθμό που προκύπτει μεταξύ των δύο. Να βρεθεί η σ.μ.π P(X=x) συναρτήσει του x.
bovid19
Εκκολαπτόμενο μέλος
Ο bovid19 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 26 ετών και Πτυχιούχος του τμήματος Οικονομικής Επιστήμης ΟΠΑ. Έχει γράψει 343 μηνύματα.

05-04-21

20:41
Ναι, δοκίμασε μέσω της συνάρτησης επιβίωσης.
bovid19
Εκκολαπτόμενο μέλος
Ο bovid19 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 26 ετών και Πτυχιούχος του τμήματος Οικονομικής Επιστήμης ΟΠΑ. Έχει γράψει 343 μηνύματα.

07-09-21

16:28
Έστω μία συνεχής τυχαία μεταβλητή 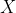 . Να δειχθεί ότι
. Να δειχθεί ότι
 = \int_{0}^{\infty}S(x)dx-\int_{-\infty}^{0}F(x)dx)
όπου
=P(X>x)) η συνάρτηση επιβίωσης και
η συνάρτηση επιβίωσης και
=P(X\leq x)) η συνάρτηση κατανομής
η συνάρτηση κατανομής
όπου
Guest 749981
Επισκέπτης
αυτή τη στιγμή δεν είναι συνδεδεμέν. Δεν έχει γράψει κανένα μήνυμα.

04-09-22

14:04
4 σημεία επιλέγονται τυχαία στην περιφέρεια ενός κύκλου. Ποια είναι η πιθανότητα να βρίσκονται όλα στο ίδιο ημικύκλιο;
Cade
Πολύ δραστήριο μέλος
Ο Cade αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Απόφοιτος λυκείου. Έχει γράψει 852 μηνύματα.

04-09-22

19:07
αν το σκέφτομαι σωστά πρέπει να βγαίνει 1/2.4 σημεία επιλέγονται τυχαία στην περιφέρεια ενός κύκλου. Ποια είναι η πιθανότητα να βρίσκονται όλα στο ίδιο ημικύκλιο;
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11,341 μηνύματα.

04-09-22

19:20
Τέσσερις δοκιμές με επιτυχία και τις τέσσερις φορές και πιθανότητα επιτυχίας 0.5 σε κάθε υποπείραμα(καθώς έχουμε ίδια πιθανότητα να επιλέξουμε σημείο σε οποιοδήποτε απο τα δύο ημικύκλια), οπότε :4 σημεία επιλέγονται τυχαία στην περιφέρεια ενός κύκλου. Ποια είναι η πιθανότητα να βρίσκονται όλα στο ίδιο ημικύκλιο;
(1/2)^4 = 1/16 ή 6.25%
Guest 749981
Επισκέπτης
αυτή τη στιγμή δεν είναι συνδεδεμέν. Δεν έχει γράψει κανένα μήνυμα.

04-09-22

19:26
Δεν είναι 2 συγκεκριμένα τα ημικύκλια.Τέσσερις δοκιμές με επιτυχία και τις τέσσερις φορές και πιθανότητα επιτυχίας 0.5 σε κάθε υποπείραμα(καθώς έχουμε ίδια πιθανότητα να επιλέξουμε σημείο σε οποιοδήποτε απο τα δύο ημικύκλια), οπότε :
(1/2)^4 = 1/16 ή 6.25%
Oof
Εκκολαπτόμενο μέλος
Ο Oof αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 20 ετών και Φοιτητής του τμήματος Ναυπηγών Μηχανολόγων Μηχανικών ΕΜΠ. Έχει γράψει 267 μηνύματα.

04-09-22

19:29
ΑκυροΤέσσερις δοκιμές με επιτυχία και τις τέσσερις φορές και πιθανότητα επιτυχίας 0.5 σε κάθε υποπείραμα(καθώς έχουμε ίδια πιθανότητα να επιλέξουμε σημείο σε οποιοδήποτε απο τα δύο ημικύκλια), οπότε :
(1/2)^4 = 1/16 ή 6.25%
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11,341 μηνύματα.

04-09-22

19:30
Ναι, είναι άπειρα, καθώς ο κύκλος έχει άπειρα σημεία οπότε μπορείς να επιλέξεις ένα απο αυτά και το αντιδιαμετρικό του και να σχηματίσεις δυο ημικύκλια.Δεν είναι 2 συγκεκριμένα τα ημικύκλια.
Αυτόματη ένωση συνεχόμενων μηνυμάτων:
Έχεις δίκιο σε αυτό που έγραψες Oof.Άκυρο
Το πρόβλημα λέει να είναι όλα στο ίδιο ημικύκλιο οπότε δεν μας ενδιαφέρει απο ποιο απο τα δυο θα επιλεχθεί το πρώτο σημείο, αρκεί τα υπόλοιπα που θα ακολουθήσουν να ανήκουν επίσης στο ίδιο.
Εαν τώρα μας ενδιαφέρει ποια είναι η πιθανότητα να ανήκουν σε ένα συγκεκριμενό απο τα δύο ημικύκλια(δεχόμενοι πάντα οτι αυτά έχουν προκαθοριστεί), τότε η πιθανότητα είναι 6.25%. Διαφορετικά είναι η διπλασία 12.5% . Αλλά προφανώς το πρόβλημα δεν ρωτάει αυτό.
Guest 586541
Επισκέπτης
αυτή τη στιγμή δεν είναι συνδεδεμέν. Δεν έχει γράψει κανένα μήνυμα.

04-09-22

19:35
Εσύ πήρες από πριν κάποια ημικύκλια στον νου σου στα οποία θα έπρεπε να βρίσκονται τα σημεία. Όμως το πρώτο και δεύτερο σημείο σίγουρα ανήκουν στο ίδιο ημικύκλιο.Τέσσερις δοκιμές με επιτυχία και τις τέσσερις φορές και πιθανότητα επιτυχίας 0.5 σε κάθε υποπείραμα(καθώς έχουμε ίδια πιθανότητα να επιλέξουμε σημείο σε οποιοδήποτε απο τα δύο ημικύκλια), οπότε :
(1/2)^4 = 1/16 ή 6.25%
Αν δεν χάνω κάτι νομίζω ότι βγαίνει 1/2.
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11,341 μηνύματα.

04-09-22

19:42
Δεν νομίζω οτι στέκει λογικά οτι τα δύο σημεία που θα ορίσουν τα όρια των ημικυκλίων συμμετέχουν στον αριθμό των τυχαία επιλεγμένων σημείων που θα ανήκουν στο ίδιο ημικύκλιο. Διότι τα άκρα του κάθε ημικυκλίου ανήκουν και στα δύο ημικύκλια ταυτόχρονα ή σε κανένα(ανάλογα πως θα το ορίσει κανείς).Εσύ πήρες από πριν κάποια ημικύκλια στον νου σου στα οποία θα έπρεπε να βρίσκονται τα σημεία. Όμως το πρώτο και δεύτερο σημείο σίγουρα ανήκουν στο ίδιο ημικύκλιο.
Αν δεν χάνω κάτι νομίζω ότι βγαίνει 1/2.
Guest 586541
Επισκέπτης
αυτή τη στιγμή δεν είναι συνδεδεμέν. Δεν έχει γράψει κανένα μήνυμα.

04-09-22

19:45
Δεν είπα αυτό.Δεν νομίζω οτι στέκει λογικά οτι τα δύο σημεία που θα ορίσουν τα όρια των ημικυκλίων συμμετέχουν στον αριθμό των τυχαία επιλεγμένων σημείων που θα ανήκουν στο ίδιο ημικύκλιο. Διότι τα άκρα του κάθε ημικυκλίου ανήκουν και στα δύο ημικύκλια ταυτόχρονα ή σε κανένα(ανάλογα πως θα το ορίσει κανείς).
Εννούσα ότι όποιο και να είναι το δεύτερο σημείο σου υποχρεωτικά θα βρεθεί στο ίδιο ημικύκλιο με το πρώτο. Είτε αποτελούν και τα δύο άκρα του ημικυκλίου είτε όχι. Διαισθητικά γίνεται αντιληπτό.
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11,341 μηνύματα.

04-09-22

19:47
Όπα, το δεύτερο τυχαία επιλεγμένο σημείο για ποιον λόγο να βρεθεί αναγκαστικά στο ίδιο ημικύκλιο με το πρώτο;Δεν είπα αυτό.
Εννούσα ότι όποιο και να είναι το δεύτερο σημείο σου υποχρεωτικά θα βρεθεί στο ίδιο ημικύκλιο με το πρώτο. Είτε αποτελούν και τα δύο άκρα του ημικυκλίου είτε όχι. Διαισθητικά γίνεται αντιληπτό.
Τουλάχιστον εγώ όπως το σκέφτηκα κάποιος ορίζει δύο ημικύκλια απο τα άπειρα ζευγάρια που υπάρχουν, εκ των προτέρων και κάνει την ερώτηση μετά. Ας μας πει και ο @Andypro που έθεσε το πρόβλημα τι ισχύει.
Oof
Εκκολαπτόμενο μέλος
Ο Oof αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 20 ετών και Φοιτητής του τμήματος Ναυπηγών Μηχανολόγων Μηχανικών ΕΜΠ. Έχει γράψει 267 μηνύματα.

04-09-22

19:51
Και με ποιο δικαίωμα ακριβώς ορίζεται στη πορεία το ημικύκλιο και όχι στο τέλος τυχαία? . Για να απαντηθεί το ερώτημα πρέπει να είναι καθορισμένα τα ημικύκλια από την αρχή ή αλλιώς ο τρόπος που καθορίζονται.
Guest 586541
Επισκέπτης
αυτή τη στιγμή δεν είναι συνδεδεμέν. Δεν έχει γράψει κανένα μήνυμα.

04-09-22

20:03
Μα αγαπητέ πώς θα γίνει αλλιώς; Η μέγιστη απόσταση είναι όταν περνά από την διάμετρο και τότε σχηματιζούν 180 μοίρες που είναι ημικύκλιο. Τουλάχιστον με βάση πώς κατάλαβα εγώ την ερώτηση.Όπα, το δεύτερο τυχαία επιλεγμένο σημείο για ποιον λόγο να βρεθεί αναγκαστικά στο ίδιο ημικύκλιο με το πρώτο;
Τουλάχιστον εγώ όπως το σκέφτηκα κάποιος ορίζει δύο ημικύκλια απο τα άπειρα ζευγάρια που υπάρχουν, εκ των προτέρων και κάνει την ερώτηση μετά. Ας μας πει και ο @Andypro που έθεσε το πρόβλημα τι ισχύει.
Τα ημικύκλια προφανώς και είναι άπειρα. Η ερώτηση τελείως σαφής δεν είναι, αλλά φαίνεται πως θες ένα εκ των άπειρων ημικυκλίων να τα περιέχει όλα. Δεν μας είπε ότι είναι fixed αυτά. Θα καθοριστούν από τις θέσεις των σημείων. Και στο κάτω-κάτω δεν θα την πόσταρε ο θεματοθέτης αν ήταν τόσο απλό το ερώτημα.
Αν τα πράγματα ήταν όπως τα έλεγες μάλλον θα έπρεπε να γράφει από ένα οποιοδήποτε ή τυχαίο ημικύκλιο.
Αυτόματη ένωση συνεχόμενων μηνυμάτων:
Από ό,τι φαίνεται καθορίζονται δυναμικά και δεν είναι στατικά...αλλιώς θα ήταν πανεύκολο το πρόβλημα. Φυσικά και η εκφώνηση δεν είναι 100% ξεκάθαρη.Και με ποιο δικαίωμα ακριβώς ορίζεται στη πορεία το ημικύκλιο και όχι στο τέλος τυχαία? . Για να απαντηθεί το ερώτημα πρέπει να είναι καθορισμένα τα ημικύκλια από την αρχή ή αλλιώς ο τρόπος που καθορίζονται.
Guest 749981
Επισκέπτης
αυτή τη στιγμή δεν είναι συνδεδεμέν. Δεν έχει γράψει κανένα μήνυμα.

04-09-22

20:08
Παράδειγμα αποδεκτού σχήματος. Δεν είναι "προκαθορισμένα" τα ημικύκλια κάπως, π.χ. βόρειο, νότιο.
Επίσης, ναι, επιλέγοντας 2 σημεία σίγουρα υπάρχει ημικύκλιο ικανό να τα συμπεριλάβει. Φαίνεται κι από το σχήμα νομίζω.
Oof
Εκκολαπτόμενο μέλος
Ο Oof αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 20 ετών και Φοιτητής του τμήματος Ναυπηγών Μηχανολόγων Μηχανικών ΕΜΠ. Έχει γράψει 267 μηνύματα.

04-09-22

20:29
Άμα τα σημεία ήταν 3 αντί για 4 ποια θα ήταν η πιθανότητα?
Guest 749981
Επισκέπτης
αυτή τη στιγμή δεν είναι συνδεδεμέν. Δεν έχει γράψει κανένα μήνυμα.

04-09-22

20:30
Άμα τα σημεία ήταν 3 αντί για 4 ποια θα ήταν η πιθανότητα?
3/4
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 6 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 67 μέλη διάβασαν αυτό το θέμα:
- mitskification
- Joji
- Panagiotis849
- GeorgePap2003
- Sherlockina
- eukleidhs1821
- Mariahj
- the purge
- kost28
- ggl
- χημεια4λαιφ
- katia.m
- KingOfPop
- sophiaa
- mpapa
- george777
- Maynard
- augustine
- tsiobieman
- igeorgeoikonomo
- notis_19
- globglogabgalab
- Unboxholics
- constansn
- Ymitheos
- DeWiN
- Georgekk
- aggelosst9
- Μάρκος Βασίλης
- spring day
- το κοριτσι του μαη
- papa2g
- SlimShady
- Nik13
- Lia 2006
- nucomer
- Johnman97
- Σωτηρία
- Εριφύλη
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki

