Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 26 ετών, Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11.416 μηνύματα.

11-09-21

14:12
το θεμα ειναι οτι τα μαθηματικα εχουν ξεφτιλιστει εντελως.δηλαδη βλεπω παιδια να ξερουν να προγραμματισουν να κανουν απιστευτα κολπα με υπολογιστες και να ναι παντελως αγραμματα στα μαθηματικα δηλαδη δωρον αδωρον αν δεν καταλαβαινουν τι κανουν.δεν ξερω τι φταιει αλλα σε λιγα χρονια θα βγαζουμε πνευματικα νεκρους πτυχιουχους που απλα θα ναι συντονισμενοι με τσιπακια
Φταίνε και οι μαθηματικοί για αυτό. Δες την ύλη, τόσες ασκήσεις με εφαρμογές θεωρημάτων σε περίεργες και εντελώς αυθαίρετες εξισώσεις και ανισώσεις. Δεν λέω οτι δεν χρειάζονται, αλλά το έχουν παρακάνει. Πιο πολύ λειτουργεί το μυαλό όταν λύνει ένα νέο πρόβλημα μέσω προγραμματισμού και επεξεργάζεται έννοιες και δεδομένα παρά όταν λύνει μια ακόμα άσκηση με Bolzano ή ΘΜΤ δοκιμάζοντας τα γνωστά στάνταρ τρικ χωρίς καμία σκέψη και intuition. Ναι στην αρχή είναι καλές αυτές οι ασκήσεις, αλλά μετά απο ένα σημείο υπάρχει κορεσμός στην σκέψη. Είναι ασκήσεις για εξοικείωση απο εκεί και πέρα δεν προσφέρουν κάτι(ούτε πνευματικά ούτε πρακτικά),οπότε ίσως τα προβλήματα θα έπρεπε να γίνουν κάπως πιο...δημιουργικά υποθέτω ;
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.928 μηνύματα.

11-09-21

14:15
μα τα τελευταια χρονια τις αποφευγουν αυτες τις ασκησεις απο οτι βλεπω.μην μου πεις οτι αυτο το τριτο θεμα δεν σου εβγαζε λιγο μυαλο για να το λυσειςΦταίνε και οι μαθηματικοί για αυτό. Δες την ύλη, τόσες ασκήσεις με εφαρμογές θεωρημάτων σε περίεργες και εντελώς αυθαίρετες εξισώσεις και ανισώσεις. Δεν λέω οτι δεν χρειάζονται, αλλά το έχουν παρακάνει. Πιο πολύ λειτουργεί το μυαλό όταν λύνει ένα νέο πρόβλημα μέσω προγραμματισμού και επεξεργάζεται έννοιες και δεδομένα παρά όταν λύνει μια ακόμα άσκηση με Bolzano ή ΘΜΤ δοκιμάζοντας τα γνωστά στάνταρ τρικ. Ναι στην αρχή είναι καλές αυτές οι ασκήσεις, αλλά μετά απο ένα σημείο υπάρχει κορεσμός στην σκέψη. Είναι ασκήσεις για εξοικείωση απο εκεί και πέρα δεν προσφέρουν κάτι(ούτε πνευματικά ούτε πρακτικά),οπότε ίσως τα προβλήματα θα έπρεπε να γίνουν κάπως πιο...δημιουργικά υποθέτω ;
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 26 ετών, Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11.416 μηνύματα.

11-09-21

15:06
Νταξ δεν θα το έλεγα, το Γ1 απαιτούσε απλά την έκφραση του χρόνου ως απόσταση δια ταχήτητα, γνωστό απο την φυσική, και απο τα μαθηματικά έναν νόμο συνημιτόνων. Το Γ2 ήταν βασική παραγώγιση και εύρεση ακρότατου ενώ το Γ3 μια αντικατάσταση τιμών στον τύπο του Γ1,και μια απλή σύγκριση τιμών των περιπτώσεων ΙΙ και ΙΙΙ ,αφού η Ι εξορισμού λόγω του Γ2 ήταν η "χειρότερη" λύση χρονικά. Θεωρώ πως ένας δυνατός μαθητής χωρίς κενάμα τα τελευταια χρονια τις αποφευγουν αυτες τις ασκησεις απο οτι βλεπω.μην μου πεις οτι αυτο το τριτο θεμα δεν σου εβγαζε λιγο μυαλο για να το λυσεις
Συγκριτικά με τις ασκήσεις στυγνής εφαρμογής θεωρημάτων καλύτερα μεν, αλλά το ιδανικό θα ήταν ο συνδυασμός των βασικών θεωρημάτων σε προβλήματα φυσικής όπως αυτό. Διότι ωθεί αβίαστα τον μαθητή να κάνει μια αντιστοίχιση των θεωρητικών εννοιών των μαθηματικών με διαισθητικές εικόνες που έχει απο την φύση. Τουλάχιστον αυτό θα ήταν το πιο λογικό για τον λογισμό κατ' εμέ. Ούτως η άλλως και ο Νεύτωνας παρατηρώντας την κίνηση των ουράνιων σωμάτων δημιούργησε τον λογισμό. Και απο εκεί αποδείχθηκε πόσο χρήσιμη είναι η εφαρμογή του και οι μεθόδοι του σε όλα τα πεδία που περιλαμβάνουν μεταβολές είτε συνδέονται πια με τον φυσικό κόσμο είτε όχι.
asdfqwerty
Πολύ δραστήριο μέλος
Ο asdfqwerty αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Φοιτητής του τμήματος Πληροφορικής & Τηλεπικοινωνιών ΕΚΠΑ. Έχει γράψει 1.347 μηνύματα.

12-09-21

21:49
Μια αλλη λυση:πριν τις προσθεσεις, πολλαπλασιασε τη μια σχεση με -1 και στα 2 μελη
Αυτόματη ένωση συνεχόμενων μηνυμάτων:
ή προσθεσε τις αναποδα (τα χ με χ και τα y με y)
Εστω:
Aρα:
Alexandros28
Δραστήριο μέλος
Ο Alexandros28 αυτή τη στιγμή δεν είναι συνδεδεμένος. Έχει γράψει 750 μηνύματα.

12-09-21

22:22
Ωραίος πολύ πιο απλό. Σε βοηθάει η μοναδικότητα εδώ και κάνει τα πράγματα πολύ απλάΜια αλλη λυση:
Εστω:με
Aρα: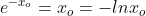
asdfqwerty
Πολύ δραστήριο μέλος
Ο asdfqwerty αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Φοιτητής του τμήματος Πληροφορικής & Τηλεπικοινωνιών ΕΚΠΑ. Έχει γράψει 1.347 μηνύματα.

13-09-21

18:30
Εστω: 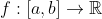 συνεχης και ισχυουν οι σχεσεις :
συνεχης και ισχυουν οι σχεσεις :
dx=f(a)-1 \\ \int_a^b f(x)dx<sinb-sina )
νδο : f(\xi)=cos{\xi} )
νδο
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 26 ετών, Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11.416 μηνύματα.

13-09-21

21:38
Μπορούμε να θεωρήσουμε συνάρτηση :Εστω:συνεχης και ισχυουν οι σχεσεις :
νδο : f(\xi)=cos{\xi} )
h(x) = f(x) - cosx , α <= x <= b .
Ολοκληρώνοντας αριστερά και δεξιά :
H(x) = F(x) - sinx + sinα , α <= x <= b , όπου F(x) = ∫f(x) dx απο α εως x .
H(α) = 0
H(b) = F(b) - sinb + sinα
Απο την δεύτερη συνθήκη ισχύει : F(b) < sinb - sinα => F(b) - sinb + sinα < 0 , οπότε H(b) < 0.
Εφόσον η H είναι παραγωγίσιμη στο (α,β) και συνεχής στο [α,β] , απο το ΘΜΤ υπάρχει τουλάχιστον ένα ζ Ε (α,β) τέτοιο ώστε :
H'(ζ) = h(ζ) = [H(b)-H(α)] / (b-α) = H(b)/(b-α) < 0 , διότι b>α και H(b) < 0 .
Άρα υπάρχει τουλάχιστον ένα ζ Ε (α,β) τέτοιο ώστε h(ζ) < 0 .
Έχουμε επίσης οτι : e^x - x - cosx >= e^x - x -1 .
Απο την γνωστή ανισότητα όμως : e^x >= x + 1 => e^x - x - 1 >= 0 για κάθε x E R , με την ισότητα να ισχύει μόνο για x = 0.
Το ολοκλήρωμα της ποσότητας e^x - x -1 λοιπόν σε ένα διάστημα [α,b] , όπου b > α, θα είναι πάντα θετικό.
Εφόσον η ποσότητα e^x - x - cosx είναι μεγαλύτερη ή ίση της προηγούμενης, και αυτής λοιπόν το ολοκλήρωμα σε ένα διάστημα [α,b] με b>α θα είναι πάντα θετικό. Ας ονοματίσουμε το αποτέλεσμα :
Α = ∫( e^x - x - cosx )dx > 0
Απο την πρώτη συνθήκη λοιπόν αφαιρούμε απο κάθε μέλος το cos(α) και προσθέτουμε 1 :
A + 1 - cos(α) = f(α) - cos(α) = h(α) .
Εφόσον Α > 0 και cos(α) <= 1 => 0 <= 1-cos(α), ξεκάθαρα η συνολική αριστερή ποσότητα : Α + 1 - cos(α) είναι θετική. Εν τέλει, μπορούμε να αποφανθούμε πως h(α) > 0 .
Εφόσον η h είναι συνεχής στο [α,b] ως συνάρτηση συνεχών συναρτήσεων και h(α)h(ζ) < 0 , απο το θεώρημα Bolzano υπάρχει τουλάχιστον ένα ξ Ε (α,ξ) C (α,b) τέτοιο ώστε h(ξ) = 0 . Δηλαδή f(ξ) - cosξ = 0 ή f(ξ) = cosξ .
asdfqwerty
Πολύ δραστήριο μέλος
Ο asdfqwerty αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Φοιτητής του τμήματος Πληροφορικής & Τηλεπικοινωνιών ΕΚΠΑ. Έχει γράψει 1.347 μηνύματα.

13-09-21

23:49
Eπειδη η συναρτηση ολοκληρωμα ειναι εκτος η λυση πρεπει να αλλαξει:Μπορούμε να θεωρήσουμε συνάρτηση :
h(x) = f(x) - cosx , α <= x <= b .
Ολοκληρώνοντας αριστερά και δεξιά :
H(x) = F(x) - sinx + sinα , α <= x <= b , όπου F(x) = ∫f(x) dx απο α εως x .
H(α) = 0
H(b) = F(b) - sinb + sinα
Απο την δεύτερη συνθήκη ισχύει : F(b) < sinb - sinα => F(b) - sinb + sinα < 0 , οπότε H(b) < 0.
Εφόσον η H είναι παραγωγίσιμη στο (α,β) και συνεχής στο [α,β] , απο το ΘΜΤ υπάρχει τουλάχιστον ένα ζ Ε (α,β) τέτοιο ώστε :
H'(ζ) = h(ζ) = [H(b)-H(α)] / (b-α) = H(b)/(b-α) < 0 , διότι b>α και H(b) < 0 .
Άρα υπάρχει τουλάχιστον ένα ζ Ε (α,β) τέτοιο ώστε h(ζ) < 0 .
Έχουμε επίσης οτι : e^x - x - cosx >= e^x - x -1 .
Απο την γνωστή ανισότητα όμως : e^x >= x + 1 => e^x - x - 1 >= 0 για κάθε x E R , με την ισότητα να ισχύει μόνο για x = 0.
Το ολοκλήρωμα της ποσότητας e^x - x -1 λοιπόν σε ένα διάστημα [α,b] , όπου b > α, θα είναι πάντα θετικό.
Εφόσον η ποσότητα e^x - x - cosx είναι μεγαλύτερη ή ίση της προηγούμενης, και αυτής λοιπόν το ολοκλήρωμα σε ένα διάστημα [α,b] με b>α θα είναι πάντα θετικό. Ας ονοματίσουμε το αποτέλεσμα :
Α = ∫( e^x - x - cosx )dx > 0
Απο την πρώτη συνθήκη λοιπόν αφαιρούμε απο κάθε μέλος το cos(α) και προσθέτουμε 1 :
A + 1 - cos(α) = f(α) - cos(α) = h(α) .
Εφόσον Α > 0 και cos(α) <= 1 => 0 <= 1-cos(α), ξεκάθαρα η συνολική αριστερή ποσότητα : Α + 1 - cos(α) είναι θετική. Εν τέλει, μπορούμε να αποφανθούμε πως h(α) > 0 .
Εφόσον η h είναι συνεχής στο [α,b] ως συνάρτηση συνεχών συναρτήσεων και h(α)h(ζ) < 0 , απο το θεώρημα Bolzano υπάρχει τουλάχιστον ένα ξ Ε (α,ξ) C (α,b) τέτοιο ώστε h(ξ) = 0 . Δηλαδή f(ξ) - cosξ = 0 ή f(ξ) = cosξ .
εχουμε αρχικα οτι
Θεωρω την συναρτηση
εστω
Θεωρουμε την συναρτηση
αρα απο bolzano στο
asdfqwerty
Πολύ δραστήριο μέλος
Ο asdfqwerty αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Φοιτητής του τμήματος Πληροφορικής & Τηλεπικοινωνιών ΕΚΠΑ. Έχει γράψει 1.347 μηνύματα.

14-09-21

22:56
Nα βρεθει το συνολο τιμων της συναρτησης:
=(sinx)^{sinx} , x\in[\frac{\pi}{6},\frac{5 \pi}{6}] )
Και μια ακομη για τον @Alexandros28
Εστω: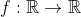 2 φορες παραγωγισιμη και ισχυουν
2 φορες παραγωγισιμη και ισχυουν
+(f'(0))^{2} = 4 )
|\leq 1 \quad \forall x \in \mathbb{R} )
νδο:
α)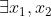 με
με  , x_2\in(0,2) ) τετοια ωστε
τετοια ωστε |\leq 1 ,|f'(x_2)|\leq 1 )
β) η=f^{2}(x)+(f'(x))^{2} ,x\in[x_1,x_2] ) παρουσιαζει ολικο μεγιστο σε εσωτερικη θεση
παρουσιαζει ολικο μεγιστο σε εσωτερικη θεση  )
γ)+f''(x_o)=0)
Αυτόματη ένωση συνεχόμενων μηνυμάτων:
Και μια ακομη για τον @Alexandros28
Εστω:
νδο:
α)
β) η
γ)
Alexandros28
Δραστήριο μέλος
Ο Alexandros28 αυτή τη στιγμή δεν είναι συνδεδεμένος. Έχει γράψει 750 μηνύματα.

14-09-21

23:28
κανοντας το γνωστο κολπο της μεθοδολογιας, η παραγωγος της f ειναι η
f'(x)=(ημχ^ημχ)(συνχ)(1+lnημχ)
ο παραγοντας ημχ^ημχ ειναι παντοτε θετικος
η εξισωση 1+lnημχ=0 ειναι αδυνατη στο πεδιο ορισμου της f επειδη αν π/6<=χ<=5π/6 τοτε μεσω του τριγωνομετρικου κυκλου ισχυει ημχ>=1/2>1/e αρα
ημχ>1/e ή
lnημχ>-1 ή
lnημχ+1>0 οποτε το προσημο της f' εξαρταται μονο απο το συνχ
μεσω μονοτονιας συνολο τιμων της f ειναι το [ριζα2/2,1]
f'(x)=(ημχ^ημχ)(συνχ)(1+lnημχ)
ο παραγοντας ημχ^ημχ ειναι παντοτε θετικος
η εξισωση 1+lnημχ=0 ειναι αδυνατη στο πεδιο ορισμου της f επειδη αν π/6<=χ<=5π/6 τοτε μεσω του τριγωνομετρικου κυκλου ισχυει ημχ>=1/2>1/e αρα
ημχ>1/e ή
lnημχ>-1 ή
lnημχ+1>0 οποτε το προσημο της f' εξαρταται μονο απο το συνχ
μεσω μονοτονιας συνολο τιμων της f ειναι το [ριζα2/2,1]
Alexandros28
Δραστήριο μέλος
Ο Alexandros28 αυτή τη στιγμή δεν είναι συνδεδεμένος. Έχει γράψει 750 μηνύματα.

14-09-21

23:59
Απο την δοθεισα ανισοτητα προκυπει f(2)=<1 και -f(0)=<1 οπου με προσθεση κατα μελη ισχυει:
f(2)-f(0)=<2 ή
f(2)-f(0)/2-0=<1
απο ΘΜΤ για την f στο [0,2] προκυπτει x1ε(0,2): f'(x1)=f(2)-f(0)/2
αρα f'(x1)=<1
απο την ιδια σχεση προκυπτει παλι f(2)>=-1 kai -f(0)>=-1 αρα ομοια για το χ1 προκυπτει f'(x1)>=-1 αρα το f'(x1) ειναι απολυτως μικροτερο ή ισο του 1. ομοια δουλευουμε για στο (-2,0).
β) επειδη η g ειναι συνεχης σε κλειστο διαστημα, παρουσιαζει μεγιστη και ελαχιστη τιμη. Η μεγιστη τιμη της g αποκλειεται να ειναι στα ακρα του διαστηματος αφου g(x1) και g(x2) ειναι μικροτερα ή ισα του 2 και μικροτερα του g(0)=4. Αρα απο θμετ υπαρχει χο ε(χ1,χ2) τετοιο ωστε η g να παρουσιαζει ολικο μεγιστο.
επειδη η g ειναι παραγωγισιμη με g'(x)=2f'(x)(f(x)+f''(x)) απο θεωρημα FERMAT στο χο ισχυει
g'(Xo)=0
το f'(xo) ειναι σιγουρα διαφορο του 0, αφου αν ηταν 0, για να ειναι ολικο μεγιστο το χο θα πρεπει g(xo)>=g(0) ή f^2(0)>=4, αδυνατο απο τα δεδομενα. Αρα f(xo)+f"(xo)=0
f(2)-f(0)=<2 ή
f(2)-f(0)/2-0=<1
απο ΘΜΤ για την f στο [0,2] προκυπτει x1ε(0,2): f'(x1)=f(2)-f(0)/2
αρα f'(x1)=<1
απο την ιδια σχεση προκυπτει παλι f(2)>=-1 kai -f(0)>=-1 αρα ομοια για το χ1 προκυπτει f'(x1)>=-1 αρα το f'(x1) ειναι απολυτως μικροτερο ή ισο του 1. ομοια δουλευουμε για στο (-2,0).
β) επειδη η g ειναι συνεχης σε κλειστο διαστημα, παρουσιαζει μεγιστη και ελαχιστη τιμη. Η μεγιστη τιμη της g αποκλειεται να ειναι στα ακρα του διαστηματος αφου g(x1) και g(x2) ειναι μικροτερα ή ισα του 2 και μικροτερα του g(0)=4. Αρα απο θμετ υπαρχει χο ε(χ1,χ2) τετοιο ωστε η g να παρουσιαζει ολικο μεγιστο.
επειδη η g ειναι παραγωγισιμη με g'(x)=2f'(x)(f(x)+f''(x)) απο θεωρημα FERMAT στο χο ισχυει
g'(Xo)=0
το f'(xo) ειναι σιγουρα διαφορο του 0, αφου αν ηταν 0, για να ειναι ολικο μεγιστο το χο θα πρεπει g(xo)>=g(0) ή f^2(0)>=4, αδυνατο απο τα δεδομενα. Αρα f(xo)+f"(xo)=0
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 26 ετών, Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11.416 μηνύματα.

15-09-21

00:05
Τούτη δεν χρειάζεται λογισμό βασικά.Nα βρεθει το συνολο τιμων της συναρτησης:
=(sinx)^{sinx} , x\in[\frac{\pi}{6},\frac{5 \pi}{6}] )
Για x = π/2 παρατηρούμε οτι f(π/2) = 1. Tόσο η βάση όσο και ο εκθέτης όμως αποκτούν ταυτόχρονα την μέγιστη δυνατή τιμή εφόσον 0 < sinx <= 1. Άρα f(x) <= 1 και f(π/2) = 1.
Επίσης : f(x) = sinx^sinx ή lnf(x) = sinx*ln(sinx) .
Η ποσότητα sinx είναι γνησίως αύξουσα στο [π/6,π/2] και γνησίως φθίνουσα στο [π/2,5π/6]. Η lnx είναι γνησίως αύξουσα στο διάστημα αυτό. Επομένως η ln(sinx) θα είναι γνησίως αύξουσα στο [π/6,π/2] και γνησίως φθίνουσα στο [π/2,π/6]. Παρατηρούμε οτι lnf(π/6) = lnf(5π/6) = -ln2/2. Οπότε η μέγιστη τιμή της lnf(x) είναι το
-ln2/2.
Εαν υψώσουμε το e σε αυτές τις ποσότητες έχουμε :
f(x) = e^(-ln2/2) = e^(ln(1/sqrt2)) = 1/sqrt2 = sqrt2/2
Το σύνολο τιμών επομένως της f θα είναι f(A) = [sqrt2/2,1]
Υπάρχουν κάποια σημεία που κανονικά θέλουν formal απόδειξη, αλλά είναι κάπως προφανή οπότε τα απέφυγα.
Alexandros28
Δραστήριο μέλος
Ο Alexandros28 αυτή τη στιγμή δεν είναι συνδεδεμένος. Έχει γράψει 750 μηνύματα.

15-09-21

00:24
Σε αυτό το σημείο σε εχασα για τα καλά. Εννοείς ελάχιστη τιμή λογικά. Αλλά και πάλι σε όλη την αιτιολόγηση κάτι δε μου κολλάει. Επειδή οι δυο παράγοντες έχουν την ίδια μονοτονία, το γινόμενο τους μεταβαλλεται με όμοιο τρόπο; Αυτό εννοείς;Η ποσότητα sinx είναι γνησίως αύξουσα στο [π/6,π/2] και γνησίως φθίνουσα στο [π/2,5π/6]. Η lnx είναι γνησίως αύξουσα στο διάστημα αυτό. Επομένως η ln(sinx) θα είναι γνησίως αύξουσα στο [π/6,π/2] και γνησίως φθίνουσα στο [π/2,π/6]. Παρατηρούμε οτι lnf(π/6) = lnf(5π/6) = -ln2/2. Οπότε η μέγιστη τιμή της lnf(x) είναι το
-ln2/2.
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 26 ετών, Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11.416 μηνύματα.

15-09-21

01:12
Ναι σόρρυ, ελάχιστη έπρεπε να λέει.Σε αυτό το σημείο σε εχασα για τα καλά. Εννοείς ελάχιστη τιμή λογικά. Αλλά και πάλι σε όλη την αιτιολόγηση κάτι δε μου κολλάει. Επειδή οι δυο παράγοντες έχουν την ίδια μονοτονία, το γινόμενο τους μεταβαλλεται με όμοιο τρόπο; Αυτό εννοείς;
Ye έχεις δίκιο,θέλει λίγο παραπάνω αιτιολόγηση. Λόγω της ιδιομορφίας που υπάρχει καθώς το x πλησιάζει το 0, προκαλεί αλλαγή της μονοτονίας της συνάρτησης πράγματι. Σε εκείνο το σημείο πρέπει να πάρεις την παράγωγο της sinx*ln(sinx) οπότε και να δείξεις οτι όταν sin(xο) = 1/e η παράγωγος μηδενίζεται. Θέλει λίγη αλλά απλή επιχειρηματολογία για να πείσεις οτι είναι ελάχιστο. Οπότε sinxo = 1/e < 1/2 = sin(π/6) δηλαδή : xo < π/6 , καθώς στο διάστημα [0,π/2] η sinx είναι γνησίως αύξουσα. So we're good γιατί το σημείο που αλλάζει τελικά η μονοτονία της sinx*ln(sinx) είναι πριν απο το π/6 .
asdfqwerty
Πολύ δραστήριο μέλος
Ο asdfqwerty αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Φοιτητής του τμήματος Πληροφορικής & Τηλεπικοινωνιών ΕΚΠΑ. Έχει γράψει 1.347 μηνύματα.

15-09-21

16:34
Εστω  ) παραγωγισιμη και ισχυει,
παραγωγισιμη και ισχυει, \cdot ln{f(x)}=e^{x} \quad \forall x\in \mathbb{R} )
νδο
α)>\sqrt{e^{x}} \quad\forall x\in \mathbb{R} )
β)νδο η f ειναι γνησιως αυξουσα και κυρτη
γ)})^{\frac{f(x)}{x}} )
δ) να λυθει η εξισωση:-f(2))+x(f(2)-f(4))=2(f(2)-f(4)) ,x\in[2,4] )
νδο
α)
β)νδο η f ειναι γνησιως αυξουσα και κυρτη
γ)
δ) να λυθει η εξισωση:
Alexandros28
Δραστήριο μέλος
Ο Alexandros28 αυτή τη στιγμή δεν είναι συνδεδεμένος. Έχει γράψει 750 μηνύματα.

15-09-21

17:36
Την έλυσα όλη εκτός από το ερώτημα γ, για το οποιο δε διαθέτω την υπομονή που χρειάζεται μεχρι στιγμης. Αμα δεν έχει ανεβάσει μέχρι αύριο απόγευμα κάποιος την λύση θα την αναλάβω εγωΕστωπαραγωγισιμη και ισχυει,
νδο
α)
β)νδο η f ειναι γνησιως αυξουσα και κυρτη
γ)
δ) να λυθει η εξισωση:-f(2))+x(f(2)-f(4))=2(f(2)-f(4)) ,x\in[2,4] )
asdfqwerty
Πολύ δραστήριο μέλος
Ο asdfqwerty αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Φοιτητής του τμήματος Πληροφορικής & Τηλεπικοινωνιών ΕΚΠΑ. Έχει γράψει 1.347 μηνύματα.

15-09-21

17:55
την ασκηση την εβαλα κυριως για το δ ερωτημα που την εχτισα για να δειξω μια αλλη ιδιοτητα των κυρτων,οχι τοσο γνωστηΤην έλυσα όλη εκτός από το ερώτημα γ, για το οποιο δε διαθέτω την υπομονή που χρειάζεται μεχρι στιγμης. Αμα δεν έχει ανεβάσει μέχρι αύριο απόγευμα κάποιος την λύση θα την αναλάβω εγω
στειλε μου σε pm πως την ελυσες.
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 26 ετών, Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11.416 μηνύματα.

15-09-21

18:00
Μια απόπειρα για το πρώτο που έκανα είναι η εξής :Εστωπαραγωγισιμη και ισχυει,
νδο
α)
β)νδο η f ειναι γνησιως αυξουσα και κυρτη
γ)
δ) να λυθει η εξισωση:-f(2))+x(f(2)-f(4))=2(f(2)-f(4)) ,x\in[2,4] )
f(x)ln(f(x)) = e^x > 0 =>
f(x)ln(f(x)) > 0
Eπειδή γνωρίζουμε πως f(x) > 0 , αναγκαστικά πρέπει ln(f(x)) > 0 => f(x) > 1 .
Επιπλέον αφού sqrt(e^x) <= 1 για x<= 0 , συμπεραίνουμε οτι η ανισότητα ισχύει για τον αρνητικό ημιάξονα.
Επομένως μένει να αποδείξουμε οτι για x > 0 ισχύει : f(x) > sqrt(e^x) .
Έστω πως δεν ισχύει. Έστω δηλαδή πως είναι : f(x) <= sqrt(e^x) .
Εφόσον e^x > sqrt(e^x) :
f(x)ln(f(x)) > sqrt(e^x) >= f(x) =>
ln(f(x)) > f(x) => ( επιτρέπεται αφού : f(x) > 0 )
ln(f(x)) > 1 =>
f(x) > e =>
Άρα : f(x)ln(f(x)) > e για κάθε χ > 0 (επιτρέπεται αφού f(x)>0 και ln(f(x)) > 0 αφού f(x) > 1 ).
Άτοπο διότι για x = 1 :
f(1)ln(f(1)) = e .
Άρα για κάθε x E R είναι : f(x) > sqrt(e^x) .
Αυτό για το α. Ίσως ασχοληθώ αργότερα με τα άλλα ερωτήματα εαν βρω χρόνο.
Alexandros28
Δραστήριο μέλος
Ο Alexandros28 αυτή τη στιγμή δεν είναι συνδεδεμένος. Έχει γράψει 750 μηνύματα.

15-09-21

18:05
το α ερωτημα βγαινει με παρομοια λογικη με του σαμ αλλα χρησιμοποιωντας την e^0.5x>x/2
asdfqwerty
Πολύ δραστήριο μέλος
Ο asdfqwerty αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Φοιτητής του τμήματος Πληροφορικής & Τηλεπικοινωνιών ΕΚΠΑ. Έχει γράψει 1.347 μηνύματα.

15-09-21

18:17
hmm , το κουρασατε λιγο περισσοτερο:  ) αυτο ισως σας λυσει τα χερια πιο ευκολα
αυτο ισως σας λυσει τα χερια πιο ευκολα
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 6 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 288 μέλη διάβασαν αυτό το θέμα:
- trifasikodiavasma
- ggl
- ioanna2007
- Hased Babis
- thepigod762
- akis_95
- Mariosm.
- Maynard
- infection54
- Jesse_
- topg
- eukleidhs1821
- bill09876
- Debugging_Demon
- mali
- Joji
- Ness
- Helen06
- Scandal
- synthnightingale
- arko
- BillyTheKid
- Magigi
- Paragontas7000
- Unboxholics
- just some guy
- george777
- Wonderkid
- IceCream05
- Abiogenesis
- GeorgePap2003
- katia.m
- giannhs2001
- paul
- Praxis
- Apocalypse
- shezza94
- desp1naa
- rempelos42
- Sherlockina
- oups
- Dimgeb
- spring day
- KingOfPop
- mpapa
- Chrisa
- Physicsstudent
- tsiobieman
- P.Dam.
- persi
- theodoraooo
- PanosBat
- kost28
- mikriarchitectonissa
- BILL KEXA
- Dr. Gl. Luminous
- Eleftheria2
- Athens2002
- bruh_234
- Miranda32
- SlimShady
- kallikd
- nucomer
- alpha.kappa
- Eeeee
- J.Cameron
- Marple
- Kitana
- F1L1PAS
- sophiaa
- VFD59
- papa2g
- το κοριτσι του μαη
- srg96
- Hopeful22
- Φινεύς
- Phys39
- Anta2004
- fairyelly
- Pharmacist01
- jYanniss
- Panagiotis849
- Kokro
- augustine
- Nikoletaant
- Mashiro@Iberan
- margik
- Mammy Nun
- Pastramis
- Σωτηρία
- Appolon
- panosveki
- Nickt23
- igeorgeoikonomo
- Steliosgkougkou
- QWERTY23
- Ameliak
- aladdin
- nimbus
- Φωτεινη Τζα.
- marian
- Georgekk
- xrisamikol
- the purge
- Theodora03
- Machris
- s93060
- Nikitas18
- Stif6
- stav.mdp
- damn
- aekaras 21
- Anthropaki
- Angelos12345
- ioannam
- Μάρκος Βασίλης
- skyway
- Nick2325
- Nala
- Manolo165
- Ryuzaki
- T C
- Devilshjoker
- El_
- George9989
- TonyMontanaEse
- globglogabgalab
- constansn
- barkos
- katerinavld
- fenia
- An_uknown_world
- Jimmis18
- maria2001
- KingPoul
- Xara
- thecrazycretan
- abcdefg12345
- Κλημεντίνη
- ale
- panagiotis G
- mechaniceng
- Giii
- calliope
- Tequila
- natalix
- Cortes
- Alexecon1991
- pepsoula
- Mariaathens
- Lia 2006
- 1205
- παιδι για κλαματα
- Alexandros36k
- alexd99
- chembam
- Specon
- Dr House
- panagiotis23
- Johnman97
- rhymeasylum
- Αννα Τσιτα
- KaterinaL
- Libertus
- LeoDel
- iminspain
- den antexw allh apotyxia
- Λαμπρινηη
- Mendel2003
- Ijt
- drosos
- Κορώνα
- JohnGreek
- Αρχηγος_β3
- alexandra_
- ΘανάσοςG4
- Dimitris9
- Birtjan
- george7cr7
- NickT
- Bgpanos
- JKTHEMAN
- nicole1982
- χημεια4λαιφ
- Stroka
- Kostakis45
- charmander
- leo41
- EiriniS20
- Αριάνα123
- MarilynSt
- iManosX13
- Nefh_
- Viedo
- Βλα
- suaimhneas
- george pol
- kristinbacktoschool
- fearless
- Rene2004
- Steffie88
- Slytherin
- jimnikol21
- Unseen skygge
- cel123
- jul25
- Thanos_D
- Ireneeneri
- tasost
- Mukumbura
- xxxtolis
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki

