eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.928 μηνύματα.

14-04-21

15:16
lim(f(x+h)-2f(x)+f(x-h))/h^2 h τεινει μηδεν
Alexandros28
Δραστήριο μέλος
Ο Alexandros28 αυτή τη στιγμή δεν είναι συνδεδεμένος. Έχει γράψει 750 μηνύματα.

14-04-21

15:55
Υποπτευομαι ντελοπιταλ. Δίνεται η συνέχεια της παραγωγου;
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.928 μηνύματα.

14-04-21

15:56
oxi 2 φορες παραγωγισιμη σκετοΥποπτευομαι ντελοπιταλ. Δίνεται η συνέχεια της παραγωγου;
asdfqwerty
Πολύ δραστήριο μέλος
Ο asdfqwerty αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Φοιτητής του τμήματος Πληροφορικής & Τηλεπικοινωνιών ΕΚΠΑ. Έχει γράψει 1.347 μηνύματα.

14-04-21

16:57
μια φορα νοσοκομειο θα κανεις και θα εκμεταλευτεις μετα
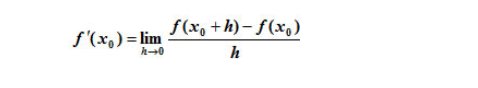
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.928 μηνύματα.

14-04-21

18:06
αυτο το ερωτημα σε παραλλαγη θα ξαναπεσει φετος και θα πεσει πολυ γελιο.μου χει καρφωθει ιδεα.
Alexandros28
Δραστήριο μέλος
Ο Alexandros28 αυτή τη στιγμή δεν είναι συνδεδεμένος. Έχει γράψει 750 μηνύματα.

14-04-21

18:56
Κατά την γνωμη μου το πιο επικίνδυνο υποψήφιο θέμα. Βρίσκεται στο σχολικό. Συνδυάζεται για πλάκα με ρυθμό μεταβολής για να το πετάξουν στο Γ
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.928 μηνύματα.

15-04-21

13:34
το πρωτο ερωτημα θελει αναλυτικη γεωμετρια ή βγαινει με τα κλασσικα της ευκλειδιας??View attachment 79417
Κατά την γνωμη μου το πιο επικίνδυνο υποψήφιο θέμα. Βρίσκεται στο σχολικό. Συνδυάζεται για πλάκα με ρυθμό μεταβολής για να το πετάξουν στο Γ
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 26 ετών, Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11.424 μηνύματα.

15-04-21

13:38
View attachment 79417
Κατά την γνωμη μου το πιο επικίνδυνο υποψήφιο θέμα. Βρίσκεται στο σχολικό. Συνδυάζεται για πλάκα με ρυθμό μεταβολής για να το πετάξουν στο Γ
Εάν έδινε την γωνία σε μοίρες και ζητούσε ρυθμούς μεταβολής όντως θα ήταν ένα καλό Γ θεματακι.
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.928 μηνύματα.

15-04-21

13:39
παντως για ασκηση του σχολικου δεν περιμενα να χει τοσο δυσκολο πρωτο ερωτημα.θα κλαιγανε πολλοι αν επεφτε κατι τετοιο
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 26 ετών, Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11.424 μηνύματα.

15-04-21

14:13
View attachment 79417
Κατά την γνωμη μου το πιο επικίνδυνο υποψήφιο θέμα. Βρίσκεται στο σχολικό. Συνδυάζεται για πλάκα με ρυθμό μεταβολής για να το πετάξουν στο Γ
Για να προσδιορίσουμε το χ αρκεί να προσδιορίσουμε την ευθεία που διέρχεται από τα Μ και Ν έτσι ώστε να βρούμε την τομή της με τον άξονα των χ. Καθώς ξέρουμε ήδη ότι Ν = (1 , θ) αρκεί απλά να βρούμε το Μ. Αλλά το Μ δεν θα είναι τίποτε άλλο από Μ = (cosθ , sinθ) , γιατί το Μ ανήκει σε κύκλο ο οποίος έχει ακτίνα 1 cm .
Εν τέλει η ευθεία γράφεται σε μορφη :
y = αx + β
Γνωρίζουμε ότι τα Μ και Ν ανήκουν στην ευθεία. Άρα για το σημείο Μ :
sinθ = α cosθ + β
Για το σημείο Ν :
θ = α + β
Τελικά από το σύστημα των δύο εξισώσεων έχουμε :
β = θ - α , οπότε :
sinθ = α cosθ + θ - α
α(cosθ - 1) = sinθ - θ
α = (sinθ - θ)/(cosθ - 1)
Επισης :
β = θ - (sinθ - θ)/(cosθ - 1)
β = (θcosθ - sinθ)/(cosθ-1)
Τώρα για y = 0 θα είναι :
αχ+β = 0
χ = -β/α
Τελικά :
χ = (θcosθ - θ)/(θ - sinθ)
Οι πράξεις έγιναν με την παραδοχή πάντα λόγω του σχήματος ότι 0 < θ < π/2 .
Alexandros28
Δραστήριο μέλος
Ο Alexandros28 αυτή τη στιγμή δεν είναι συνδεδεμένος. Έχει γράψει 750 μηνύματα.

15-04-21

14:28
Διαφορετική λύση: Τα διανύσματα ΡΜ,ΡΝ είναι συνεχώς παράλληλα , επομενως η οριζουσα (det) αυτών ισούται με 0.
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.928 μηνύματα.

15-04-21

15:51
μαλιστα καλα το ψιλιαστηκα οτι θελει αναλυτικη γεωμετρια.πολυ ωραια η λυση σου.αραγε καμια λυση με ευκλειδια γεωμετρια να υπαρχει??Για να προσδιορίσουμε το χ αρκεί να προσδιορίσουμε την ευθεία που διέρχεται από τα Μ και Ν έτσι ώστε να βρούμε την τομή της με τον άξονα των χ. Καθώς ξέρουμε ήδη ότι Ν = (1 , θ) αρκεί απλά να βρούμε το Μ. Αλλά το Μ δεν θα είναι τίποτε άλλο από Μ = (cosθ , sinθ) , γιατί το Μ ανήκει σε κύκλο ο οποίος έχει ακτίνα 1 cm .
Εν τέλει η ευθεία γράφεται σε μορφη :
y = αx + β
Γνωρίζουμε ότι τα Μ και Ν ανήκουν στην ευθεία. Άρα για το σημείο Μ :
sinθ = α cosθ + β
Για το σημείο Ν :
θ = α + β
Τελικά από το σύστημα των δύο εξισώσεων έχουμε :
β = θ - α , οπότε :
sinθ = α cosθ + θ - α
α(cosθ - 1) = sinθ - θ
α = (sinθ - θ)/(cosθ - 1)
Επισης :
β = θ - (sinθ - θ)/(cosθ - 1)
β = (θcosθ - sinθ)/(cosθ-1)
Τώρα για y = 0 θα είναι :
αχ+β = 0
χ = -β/α
Τελικά :
χ = (θcosθ - θ)/(θ - sinθ)
Οι πράξεις έγιναν με την παραδοχή πάντα λόγω του σχήματος ότι 0 < θ < π/2 .
Αυτόματη ένωση συνεχόμενων μηνυμάτων:
σωστος.κοιτα να δεις που εμπλεκονται και διανυσματα αμα το θες.μπορεις και να παρεις τα PM MN διανυσματα το ιδιο βγαινει.και με συντελεστες διευθυνσης βγαινει καθως με βαση τη μορφη του σχηματος τηρουνται οι περιορισμοιΔιαφορετική λύση: Τα διανύσματα ΡΜ,ΡΝ είναι συνεχώς παράλληλα , επομενως η οριζουσα (det) αυτών ισούται με 0.
asdfqwerty
Πολύ δραστήριο μέλος
Ο asdfqwerty αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Φοιτητής του τμήματος Πληροφορικής & Τηλεπικοινωνιών ΕΚΠΑ. Έχει γράψει 1.347 μηνύματα.

15-04-21

16:31
ειναι και η λυση που δινει το σχολικομαλιστα καλα το ψιλιαστηκα οτι θελει αναλυτικη γεωμετρια.πολυ ωραια η λυση σου.αραγε καμια λυση με ευκλειδια γεωμετρια να υπαρχει??
Αυτόματη ένωση συνεχόμενων μηνυμάτων:
σωστος.κοιτα να δεις που εμπλεκονται και διανυσματα αμα το θες.μπορεις και να παρεις τα PM MN διανυσματα το ιδιο βγαινει.και με συντελεστες διευθυνσης βγαινει καθως με βαση τη μορφη του σχηματος τηρουνται οι περιορισμοι
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 26 ετών, Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11.424 μηνύματα.

15-04-21

16:37
μαλιστα καλα το ψιλιαστηκα οτι θελει αναλυτικη γεωμετρια.πολυ ωραια η λυση σου.αραγε καμια λυση με ευκλειδια γεωμετρια να υπαρχει??
Αυτόματη ένωση συνεχόμενων μηνυμάτων:
σωστος.κοιτα να δεις που εμπλεκονται και διανυσματα αμα το θες.μπορεις και να παρεις τα PM MN διανυσματα το ιδιο βγαινει.και με συντελεστες διευθυνσης βγαινει καθως με βαση τη μορφη του σχηματος τηρουνται οι περιορισμοι
Why not i guess...
NPA και MPB όμοια γιατί έχουν παράλληλες και τις τρεις πλευρές. Οπότε θα ισχύει :
PB/MB = PA/NA
Έχουμε όμως :
PB = cosθ+x
MB = sinθ
PA = x+1
NA = θ
(cosθ + x)/sinθ = (1+x)/θ =>
θcosθ-sinθ = xsinθ -xθ =>
x = (θcosθ-sinθ)/(sinθ-θ)
Και επειδή το x βρίσκεται στον αρνητικό ημιάξονα,αλγεβρικά έχουμε :
x = (θcosθ-sinθ)/(θ-sinθ) cm
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.928 μηνύματα.

15-04-21

16:42
eipa και εγω.εχεις κανει ενα λαθος ομως.επειδη ειναι μηκος το ΡΒ ειναι ΡΒ=cosθ-χWhy not i guess...
View attachment 79488
NPA και MPB όμοια γιατί έχουν παράλληλες και τις τρεις πλευρές. Οπότε θα ισχύει :
PB/MB = PA/NA
Έχουμε όμως :
PB = cosθ+x
MB = sinθ
PA = x+1
NA = θ
(cosθ + x)/sinθ = (1+x)/θ =>
θcosθ-sinθ = xsinθ -xθ =>
x = (θcosθ-sinθ)/(sinθ-θ)
Και επειδή το x βρίσκεται στον αρνητικό ημιάξονα,αλγεβρικά έχουμε :
x = (θcosθ-sinθ)/(θ-sinθ) cm
Αυτόματη ένωση συνεχόμενων μηνυμάτων:
τα τριγωνα που βαλες ειναι ομοια γτ ειναι ορθογωνια και εχουν μια κοινη γωνια.
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 26 ετών, Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11.424 μηνύματα.

15-04-21

16:52
eipa και εγω.εχεις κανει ενα λαθος ομως.επειδη ειναι μηκος το ΡΒ ειναι ΡΒ=cosθ-χ
Αυτόματη ένωση συνεχόμενων μηνυμάτων:
τα τριγωνα που βαλες ειναι ομοια γτ ειναι ορθογωνια και εχουν μια κοινη γωνια.
Δεν κάνω λάθος,το λαμβάνω υπόψιν στο τέλος. Επειδή ακριβώς είναι μήκος δεν μπορείς να πεις :
PB = cosθ-x διότι δεν υπάρχει αρνητικό μήκος(στην ευκλείδια γεωμετρία τουλάχιστον
 ),και αυτή η ποσότητα στην γενική περίπτωση μπορεί να είναι αρνητική. Διαφορετικά πάλι έχεις καταλήξει στην αναλυτική γεωμετρία. Που ούτως η άλλως δηλαδή εκεί ανήκει το πρόβλημα γιατί μας έχει δώσει σημεία και έχει ορίσει σύστημα αξόνων.
),και αυτή η ποσότητα στην γενική περίπτωση μπορεί να είναι αρνητική. Διαφορετικά πάλι έχεις καταλήξει στην αναλυτική γεωμετρία. Που ούτως η άλλως δηλαδή εκεί ανήκει το πρόβλημα γιατί μας έχει δώσει σημεία και έχει ορίσει σύστημα αξόνων.eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.928 μηνύματα.

15-04-21

16:58
μα το χ ετσι οπως ειναι ορισμενο στο σχημα προφανως ειναι αρνητικο οποτε το -χ ειναι η θετικη ποσοτητα.νομιζω οτι το ορθο να το πεις απο την αρχη.στο τελος που το βαζεις κανεις δεν ξερει τι γινεται με τον αριθμητη παρα μονο με τον παρονομαστη που ξερεις τη σχεση του sinθ με το θΔεν κάνω λάθος,το λαμβάνω υπόψιν στο τέλος. Επειδή ακριβώς είναι μήκος δεν μπορείς να πεις :
PB = cosθ-x διότι δεν υπάρχει αρνητικό μήκος(στην ευκλείδια γεωμετρία τουλάχιστον),και αυτή η ποσότητα στην γενική περίπτωση μπορεί να είναι αρνητική. Διαφορετικά πάλι έχεις καταλήξει στην αναλυτική γεωμετρία. Που ούτως η άλλως δηλαδή εκεί ανήκει το πρόβλημα γιατί μας έχει δώσει σημεία και έχει ορίσει σύστημα αξόνων.
Αυτόματη ένωση συνεχόμενων μηνυμάτων:
ωραια λυση παντως αρκει να σου κοψει να φερεις την καθετο.
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 26 ετών, Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11.424 μηνύματα.

15-04-21

17:06
μα το χ ετσι οπως ειναι ορισμενο στο σχημα προφανως ειναι αρνητικο οποτε το -χ ειναι η θετικη ποσοτητα.νομιζω οτι το ορθο να το πεις απο την αρχη.στο τελος που το βαζεις κανεις δεν ξερει τι γινεται με τον αριθμητη παρα μονο με τον παρονομαστη που ξερεις τη σχεση του sinθ με το θ
Δεν διαφωνώ, για αυτό ακριβώς στο τέλος της λύσης πολλαπλασιάζω με -1 και λεω επίσης :
"Και επειδή το x βρίσκεται στον αρνητικό ημιάξονα,αλγεβρικά η τιμή του χ είναι : ..." .
Και πάλι αναρωτιέμαι όμως πως θα μπορούσες στην Ευκλείδια γεωμετρία να μιλήσεις για αρνητικό μήκος πλευράς;
Εαν θέλουμε να είμαστε αυστηροί πάντως, ούτως η άλλως δεν υπάρχει αρνητικό μήκος σε ένα φυσικό πρόβλημα. Η σωστή ερμηνεία του πλην είναι προς τα αριστερά.
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.928 μηνύματα.

15-04-21

17:08
το λεω επειδη ετσι οπως εχει δοθει στο σχημα το χ<0.οποτε βαζουμε το απολυτοχ.τεσπα μην κολλαμε σε λεπτομερειες.φοβερη η λυση σου και μακαρι να ενθαρρυνθουν πολλοι να διδασκουν τετοιες λυσεις και οχι τυφλοσουρτηδεςΔεν διαφωνώ, για αυτό ακριβώς στο τέλος της λύσης πολλαπλασιάζω με -1 και λεω επίσης :
"Και επειδή το x βρίσκεται στον αρνητικό ημιάξονα,αλγεβρικά η τιμή του χ είναι : ..." .
Και πάλι αναρωτιέμαι όμως πως θα μπορούσες στην Ευκλείδια γεωμετρία να μιλήσεις για αρνητικό μήκος πλευράς;
Εαν θέλουμε να είμαστε αυστηροί πάντως, ούτως η άλλως δεν υπάρχει αρνητικό μήκος σε ένα φυσικό πρόβλημα. Η σωστή ερμηνεία του πλην είναι προς τα αριστερά.
Samael
Τιμώμενο Μέλος
Ο Samael αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 26 ετών, Πτυχιούχος του τμήματος Ηλεκτρολόγων & Ηλεκτρονικών Μηχανικών ΠΑΔΑ και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 11.424 μηνύματα.

15-04-21

17:18
το λεω επειδη ετσι οπως εχει δοθει στο σχημα το χ<0.οποτε βαζουμε το απολυτοχ.τεσπα μην κολλαμε σε λεπτομερειες.φοβερη η λυση σου και μακαρι να ενθαρρυνθουν πολλοι να διδασκουν τετοιες λυσεις και οχι τυφλοσουρτηδες
Θα μπορούσα και εγώ να είμαι πιο ξεκάθαρος ως προς το notation για αποφυγή τυχών παρερμηνείας των συμβόλων όντως. Πάντως ναι μπορείς να βάλεις όπου χ το (Οχ) στην λύση πάνω και κάτω που λεω για αλγεβρική τιμή να γράψεις χ = ... .
Η λύση μέσω της Ευκλείδειας γεωμετρίας είναι η πιο κομψή νομίζω και εγώ, άσχετα που δεν είναι και το πιο δυνατό μου σημείο.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 2 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 288 μέλη διάβασαν αυτό το θέμα:
- trifasikodiavasma
- ggl
- ioanna2007
- Hased Babis
- thepigod762
- akis_95
- Mariosm.
- Maynard
- infection54
- Jesse_
- topg
- eukleidhs1821
- bill09876
- Debugging_Demon
- mali
- Joji
- Ness
- Helen06
- Scandal
- synthnightingale
- arko
- BillyTheKid
- Magigi
- Paragontas7000
- Unboxholics
- just some guy
- george777
- Wonderkid
- IceCream05
- Abiogenesis
- GeorgePap2003
- katia.m
- giannhs2001
- paul
- Praxis
- Apocalypse
- shezza94
- desp1naa
- rempelos42
- Sherlockina
- oups
- Dimgeb
- spring day
- KingOfPop
- mpapa
- Chrisa
- Physicsstudent
- tsiobieman
- P.Dam.
- persi
- theodoraooo
- PanosBat
- kost28
- mikriarchitectonissa
- BILL KEXA
- Dr. Gl. Luminous
- Eleftheria2
- Athens2002
- bruh_234
- Miranda32
- SlimShady
- kallikd
- nucomer
- alpha.kappa
- Eeeee
- J.Cameron
- Marple
- Kitana
- F1L1PAS
- sophiaa
- VFD59
- papa2g
- το κοριτσι του μαη
- srg96
- Hopeful22
- Φινεύς
- Phys39
- Anta2004
- fairyelly
- Pharmacist01
- jYanniss
- Panagiotis849
- Kokro
- augustine
- Nikoletaant
- Mashiro@Iberan
- margik
- Mammy Nun
- Pastramis
- Σωτηρία
- Appolon
- panosveki
- Nickt23
- igeorgeoikonomo
- Steliosgkougkou
- QWERTY23
- Ameliak
- aladdin
- nimbus
- Φωτεινη Τζα.
- marian
- Georgekk
- xrisamikol
- the purge
- Theodora03
- Machris
- s93060
- Nikitas18
- Stif6
- stav.mdp
- damn
- aekaras 21
- Anthropaki
- Angelos12345
- ioannam
- Μάρκος Βασίλης
- skyway
- Nick2325
- Nala
- Manolo165
- Ryuzaki
- T C
- Devilshjoker
- El_
- George9989
- TonyMontanaEse
- globglogabgalab
- constansn
- barkos
- katerinavld
- fenia
- An_uknown_world
- Jimmis18
- maria2001
- KingPoul
- Xara
- thecrazycretan
- abcdefg12345
- Κλημεντίνη
- ale
- panagiotis G
- mechaniceng
- Giii
- calliope
- Tequila
- natalix
- Cortes
- Alexecon1991
- pepsoula
- Mariaathens
- Lia 2006
- 1205
- παιδι για κλαματα
- Alexandros36k
- alexd99
- chembam
- Specon
- Dr House
- panagiotis23
- Johnman97
- rhymeasylum
- Αννα Τσιτα
- KaterinaL
- Libertus
- LeoDel
- iminspain
- den antexw allh apotyxia
- Λαμπρινηη
- Mendel2003
- Ijt
- drosos
- Κορώνα
- JohnGreek
- Αρχηγος_β3
- alexandra_
- ΘανάσοςG4
- Dimitris9
- Birtjan
- george7cr7
- NickT
- Bgpanos
- JKTHEMAN
- nicole1982
- χημεια4λαιφ
- Stroka
- Kostakis45
- charmander
- leo41
- EiriniS20
- Αριάνα123
- MarilynSt
- iManosX13
- Nefh_
- Viedo
- Βλα
- suaimhneas
- george pol
- kristinbacktoschool
- fearless
- Rene2004
- Steffie88
- Slytherin
- jimnikol21
- Unseen skygge
- cel123
- jul25
- Thanos_D
- Ireneeneri
- tasost
- Mukumbura
- xxxtolis
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki

