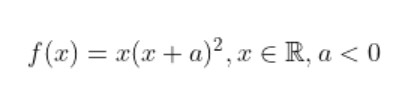eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.957 μηνύματα.

23-02-21

16:25
o ισχυρισμος ισχυει σιγουρα αν μιλας σε διαστημα!Δεν υπάρχει περίπτωση να πέσει. Το μισό mathematica έχει δώσει πάνω από 5 αποδείξεις ότι ισχύει ο ισχυρισμός φαντάσου τι έχει να γίνει από μαθητές
Alexandros28
Δραστήριο μέλος
Ο Alexandros28 αυτή τη στιγμή δεν είναι συνδεδεμένος. Έχει γράψει 750 μηνύματα.

23-02-21

16:33
Ναι σωστά.o ισχυρισμος ισχυει σιγουρα αν μιλας σε διαστημα!
asdfqwerty
Πολύ δραστήριο μέλος
Ο asdfqwerty αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Φοιτητής του τμήματος Πληροφορικής & Τηλεπικοινωνιών ΕΚΠΑ. Έχει γράψει 1.347 μηνύματα.
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.957 μηνύματα.

23-03-21

20:04
πονηρη ασκηση. f'(x)=3x^2+4ax+a^2 Δ=4α^2>0 αφου α<0.αρα το τριωνυμο εχει 2 διακεκριμενες ριζες τις χ1=-α και χ2=-α/3 f'(x)>0 εκτος του [-α/3,-α] και f'(x)<0 στο (-α/3,-α)
1η περιπτωση) χ1=-α>3 δηλαδη α<-3 τότε χ2=-α/3>1 υπάρχει τουλάχιστον ένα υποδιαστημα [κ,λ] στο [1,3] τετοιο ώστε f'(χ)>0 για καθε χ στο [κ,λ] αρα δεν ειναι γνησιως φθινουσα στο [1,3]
2η περιπτωση) 3>χ1=-α δηλαδη α>-3 τότε χ2=-α/3<1 υπάρχει τουλάχιστον ένα υποδιαστημα [κ,λ] στο [1,3] τετοιο ώστε f'(χ)>0 για καθε χ στο [κ,λ] άρα δεν είναι γνησίως φθίνουσα στο [1,3]
3η περίπτωση) χ1=-α=3 δηλαδή α=-3 και χ2=1/3 f'(x)<0 στο (1/3,3) κατα συνεπεια στο [1/3,3] είναι γνησίως φθίνουσα άρα και στο [1,3]
1η περιπτωση) χ1=-α>3 δηλαδη α<-3 τότε χ2=-α/3>1 υπάρχει τουλάχιστον ένα υποδιαστημα [κ,λ] στο [1,3] τετοιο ώστε f'(χ)>0 για καθε χ στο [κ,λ] αρα δεν ειναι γνησιως φθινουσα στο [1,3]
2η περιπτωση) 3>χ1=-α δηλαδη α>-3 τότε χ2=-α/3<1 υπάρχει τουλάχιστον ένα υποδιαστημα [κ,λ] στο [1,3] τετοιο ώστε f'(χ)>0 για καθε χ στο [κ,λ] άρα δεν είναι γνησίως φθίνουσα στο [1,3]
3η περίπτωση) χ1=-α=3 δηλαδή α=-3 και χ2=1/3 f'(x)<0 στο (1/3,3) κατα συνεπεια στο [1/3,3] είναι γνησίως φθίνουσα άρα και στο [1,3]
asdfqwerty
Πολύ δραστήριο μέλος
Ο asdfqwerty αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Φοιτητής του τμήματος Πληροφορικής & Τηλεπικοινωνιών ΕΚΠΑ. Έχει γράψει 1.347 μηνύματα.

23-03-21

22:37
μπορει να βγει γρηγοροτερα κιολας: εδειξες οτι η συναρτηση ειναι γνησιως φθινουυσα στο [-α/3,-α]πονηρη ασκηση. f'(x)=3x^2+4ax+a^2 Δ=4α^2>0 αφου α<0.αρα το τριωνυμο εχει 2 διακεκριμενες ριζες τις χ1=-α και χ2=-α/3 f'(x)>0 εκτος του [-α/3,-α] και f'(x)<0 στο (-α/3,-α)
1η περιπτωση) χ1=-α>3 δηλαδη α<-3 τότε χ2=-α/3>1 υπάρχει τουλάχιστον ένα υποδιαστημα [κ,λ] στο [1,3] τετοιο ώστε f'(χ)>0 για καθε χ στο [κ,λ] αρα δεν ειναι γνησιως φθινουσα στο [1,3]
2η περιπτωση) 3>χ1=-α δηλαδη α>-3 τότε χ2=-α/3<1 υπάρχει τουλάχιστον ένα υποδιαστημα [κ,λ] στο [1,3] τετοιο ώστε f'(χ)>0 για καθε χ στο [κ,λ] άρα δεν είναι γνησίως φθίνουσα στο [1,3]
3η περίπτωση) χ1=-α=3 δηλαδή α=-3 και χ2=1/3 f'(x)<0 στο (1/3,3) κατα συνεπεια στο [1/3,3] είναι γνησίως φθίνουσα άρα και στο [1,3]
γνωριζεις απο υποθεση οτι ειναι φθινουσα στο [1,3] αρα το [1,3] ειναι υποσυνολο του [-α/3,-α]
αρα: -α/3<=1 ^ -α>=3 <=> α>=-3 ^ α<=-3 => α=-3
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.957 μηνύματα.

23-03-21

23:33
nai εχεις δικιο.απλα δεν σκεφτηκα οτι εφοσον βγαζω γενικα το προσημο της παραγωγου εχω αμεσο συμπερασμα για μονοτονια.ναι εχεις δικιο απλα και το δικο μου ηταν μια πιο safe λυσημπορει να βγει γρηγοροτερα κιολας: εδειξες οτι η συναρτηση ειναι γνησιως φθινουυσα στο [-α/3,-α]
γνωριζεις απο υποθεση οτι ειναι φθινουσα στο [1,3] αρα το [1,3] ειναι υποσυνολο του [-α/3,-α]
αρα: -α/3<=1 ^ -α>=3 <=> α>=-3 ^ α<=-3 => α=-3
Alexandros28
Δραστήριο μέλος
Ο Alexandros28 αυτή τη στιγμή δεν είναι συνδεδεμένος. Έχει γράψει 750 μηνύματα.

23-03-21

23:40
Να δειχτεί πως αν για μια παραγωγίσιμη συνάρτηση f ισχύει: f’(x)≠0 ,xεΔ
τότε η f είναι γνησίως μονότονη στο Δ.
τότε η f είναι γνησίως μονότονη στο Δ.
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.957 μηνύματα.

24-03-21

00:21
αυτο νομιζω περσι την ειχε ανεβασει περσι τη λυση ο μαρκος ο βασιλης.πολυ ωραιο θεμα.με μεγιστη και ελαχιστη τιμη και φερματ βγαινει ψαχτε στο φορουμ θα τη βρειτεΝα δειχτεί πως αν για μια παραγωγίσιμη συνάρτηση f ισχύει: f’(x)≠0 ,xεΔ
τότε η f είναι γνησίως μονότονη στο Δ.
bovid19
Εκκολαπτόμενο μέλος
Ο bovid19 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 27 ετών και Πτυχιούχος του τμήματος Οικονομικής Επιστήμης ΟΠΑ. Έχει γράψει 344 μηνύματα.

24-03-21

00:27
Αν το Δ είναι διάστημα απλά πρέπει να δείξεις ότι μία συνεχής 1-1 συνάρτηση είναι και γνησίως μονότονη.
Περισσότερα εδώ: https://www.mathematica.gr/forum/viewtopic.php?t=12520
Περισσότερα εδώ: https://www.mathematica.gr/forum/viewtopic.php?t=12520
Alexandros28
Δραστήριο μέλος
Ο Alexandros28 αυτή τη στιγμή δεν είναι συνδεδεμένος. Έχει γράψει 750 μηνύματα.

24-03-21

00:30
Σωστά. Ουσιαστικά η διαδικασία που αναφέρεις είναι η απόδειξη του θεωρήματος Darboux, για όσους θέλουν να την δουν πιο αναλυτικά.αυτο νομιζω περσι την ειχε ανεβασει περσι τη λυση ο μαρκος ο βασιλης.πολυ ωραιο θεμα.με μεγιστη και ελαχιστη τιμη και φερματ βγαινει ψαχτε στο φορουμ θα τη βρειτε
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.957 μηνύματα.

24-03-21

13:45

Άσκηση στα μαθηματικά κατεύθυνσης
Νομιζω καλως απορρίπτεις τα άκρα. Το Χ είναι εσωτερικό σημείο του διαστήματος που πήρες. απλα κατι δεν μου κολλαει επειδη μιλαω κοντα στο οριο της παραγωγου που πηρα.μαλλον σωστα τα λεω 1587653021 υπαρχει καποιος τροπος να γραφεις μαθηματικα συμβολα εδω?
Αυτόματη ένωση συνεχόμενων μηνυμάτων:
αν εχεις οτι η παραγωγος ειναι διαφορη του μηδενος σε ενα διαστημα ειναι 1-1 οποτε μπορεις να το αναγεις και σε αυτο που λεςΑν το Δ είναι διάστημα απλά πρέπει να δείξεις ότι μία συνεχής 1-1 συνάρτηση είναι και γνησίως μονότονη.
Περισσότερα εδώ: https://www.mathematica.gr/forum/viewtopic.php?t=12520
bovid19
Εκκολαπτόμενο μέλος
Ο bovid19 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 27 ετών και Πτυχιούχος του τμήματος Οικονομικής Επιστήμης ΟΠΑ. Έχει γράψει 344 μηνύματα.

24-03-21

14:26
Ωραία η απόδειξη. Αλλά θεωρώ ότι οι μαθητές αξίζει να κρατήσουν ότι Συνέχεια + 1-1 => Γνήσια μονοτονία. Η f'(x)≠0 είναι πιο απαιτητική συνθήκη (καθώς υποθέτει ότι η f είναι και παραγωγίσιμη).η φοβερη αποδειξη του μαρκου βασιλη σε αυτο που ρωτησε ο αλεξανδρος.περαν του δυσκολου να σκεφτεις το θεωρημα μεγιστης και ελαχιστης τιμης πρεπει να αποδειξεις οτι δεν γινεται στα ακρα ελαχιστο ωστε να κανεις φερματ.δεν πιστευω οτι μπορει να τεθει ποτε κατι τετοιο αλλα καλο ειναι να δειτε τον τροπο σκεψης
Άσκηση στα μαθηματικά κατεύθυνσης
Νομιζω καλως απορρίπτεις τα άκρα. Το Χ είναι εσωτερικό σημείο του διαστήματος που πήρες. απλα κατι δεν μου κολλαει επειδη μιλαω κοντα στο οριο της παραγωγου που πηρα.μαλλον σωστα τα λεω 1587653021 υπαρχει καποιος τροπος να γραφεις μαθηματικα συμβολα εδω?www.ischool.gr
Αυτόματη ένωση συνεχόμενων μηνυμάτων:
αν εχεις οτι η παραγωγος ειναι διαφορη του μηδενος σε ενα διαστημα ειναι 1-1 οποτε μπορεις να το αναγεις και σε αυτο που λες
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.957 μηνύματα.

24-03-21

14:29
εχω την αισθηση οτι αυτο το παιρνουν ετοιμο συνεχεια + 1-1 γνησιως μονοτονη χωρις αποδειξη???νομιζω ετσι ελεγε ο μαρκος περσιΩραία η απόδειξη. Αλλά θεωρώ ότι οι μαθητές αξίζει να κρατήσουν ότι Συνέχεια + 1-1 => Γνήσια μονοτονία. Η f'(x)≠0 είναι πιο απαιτητική συνθήκη (καθώς υποθέτει ότι η f είναι και παραγωγίσιμη).
bovid19
Εκκολαπτόμενο μέλος
Ο bovid19 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 27 ετών και Πτυχιούχος του τμήματος Οικονομικής Επιστήμης ΟΠΑ. Έχει γράψει 344 μηνύματα.

24-03-21

14:31
Όντως; Αν είναι έτσι με ένα Rolle έχει τελειώσει η άσκηση.εχω την αισθηση οτι αυτο το παιρνουν ετοιμο συνεχεια + 1-1 γνησιως μονοτονη χωρις αποδειξη???νομιζω ετσι ελεγε ο μαρκος περσι
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.957 μηνύματα.

24-03-21

14:36
λες για την αποδειξη με την παραγωγο?κατι τετοιο ειχε παρει το ματι μουΌντως; Αν είναι έτσι με ένα Rolle έχει τελειώσει η άσκηση.
Alexandros28
Δραστήριο μέλος
Ο Alexandros28 αυτή τη στιγμή δεν είναι συνδεδεμένος. Έχει γράψει 750 μηνύματα.
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.957 μηνύματα.

24-03-21

15:10
ειναι για καθε α,β ανηκει r?
Alexandros28
Δραστήριο μέλος
Ο Alexandros28 αυτή τη στιγμή δεν είναι συνδεδεμένος. Έχει γράψει 750 μηνύματα.
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.957 μηνύματα.

24-03-21

15:55
πολυ ωραια ασκηση.εστω οτι α<β απο την σχεση που εχουμε g(a)-g(b)>=-απολυτο(α-β)=α-β αρα g(a)-a>=g(b)-b αρα f(a)+a>=f(b)+b f(a)-f(b)>=b-a>0 αρα f(a)>f(b) αρα γνησιως φθινουσα
bovid19
Εκκολαπτόμενο μέλος
Ο bovid19 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 27 ετών και Πτυχιούχος του τμήματος Οικονομικής Επιστήμης ΟΠΑ. Έχει γράψει 344 μηνύματα.

24-03-21

15:59
Βάζεις όπου α το x και όπου β κάποιο τυχαίο πραγματικό x0.
Θα ισχύει |g(x)-g(x0)|<=|x-x0| <=> -|x-x0|<= g(x)-g(x0)<=|x-x0|. Με κ.π. δείχνεις ότι η g είναι συνεχής οπότε και η f θα είναι συνεχής. Έστω ότι η f δεν είναι 1-1 δηλαδή ότι υπάρχουν πραγματικά x1,x2 τ.ω. f(x1)=f(x2) με x1,x2 διάφορα. Τότε g(x1)-2*x1=g(x2)-2*x2 <=> [g(x2)-g(x1)]/(x2-x1) = 2 που είναι άτοπο διότι
-1 <= [g(x2)-g(x1)]/(x2-x1) <= 1. Άρα η f είναι 1-1 και συνεχής και με το λινκ παραπάνω δείχνουμε πως είναι και γνησίως μονότονη. Επίσης f(1)-f(0)=g(1)-g(0)-2<0 επειδή |g(1)-g(0)|<= 1 επομένως g(1)- g(0) <= 1 < 2 και τελικά f(1)<f(0) άρα είναι γνησίως φθίνουσα
Edit: Τελικά υπήρχε πιο κομψός τρόπος, κάπως έτσι τα έλυνα εκείνη τη χρονιά και με καντήλιαζε ο καθήγητης.
Θα ισχύει |g(x)-g(x0)|<=|x-x0| <=> -|x-x0|<= g(x)-g(x0)<=|x-x0|. Με κ.π. δείχνεις ότι η g είναι συνεχής οπότε και η f θα είναι συνεχής. Έστω ότι η f δεν είναι 1-1 δηλαδή ότι υπάρχουν πραγματικά x1,x2 τ.ω. f(x1)=f(x2) με x1,x2 διάφορα. Τότε g(x1)-2*x1=g(x2)-2*x2 <=> [g(x2)-g(x1)]/(x2-x1) = 2 που είναι άτοπο διότι
-1 <= [g(x2)-g(x1)]/(x2-x1) <= 1. Άρα η f είναι 1-1 και συνεχής και με το λινκ παραπάνω δείχνουμε πως είναι και γνησίως μονότονη. Επίσης f(1)-f(0)=g(1)-g(0)-2<0 επειδή |g(1)-g(0)|<= 1 επομένως g(1)- g(0) <= 1 < 2 και τελικά f(1)<f(0) άρα είναι γνησίως φθίνουσα
Edit: Τελικά υπήρχε πιο κομψός τρόπος, κάπως έτσι τα έλυνα εκείνη τη χρονιά και με καντήλιαζε ο καθήγητης.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 1 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 290 μέλη διάβασαν αυτό το θέμα:
- mikke
- hihat1
- thepigod762
- 98.8%chimpanzee
- trifasikodiavasma
- ggl
- ioanna2007
- Hased Babis
- akis_95
- Mariosm.
- Maynard
- infection54
- Jesse_
- topg
- eukleidhs1821
- bill09876
- Debugging_Demon
- mali
- Joji
- Ness
- Helen06
- Scandal
- synthnightingale
- arko
- BillyTheKid
- Magigi
- nearos
- Paragontas7000
- Unboxholics
- just some guy
- george777
- Wonderkid
- IceCream05
- Abiogenesis
- GeorgePap2003
- katia.m
- giannhs2001
- paul
- Praxis
- Apocalypse
- shezza94
- desp1naa
- rempelos42
- Sherlockina
- oups
- Dimgeb
- spring day
- KingOfPop
- mpapa
- Chrisa
- Physicsstudent
- tsiobieman
- P.Dam.
- persi
- theodoraooo
- PanosBat
- kost28
- mikriarchitectonissa
- BILL KEXA
- Dr. Gl. Luminous
- Eleftheria2
- Athens2002
- bruh_234
- Miranda32
- SlimShady
- kallikd
- nucomer
- alpha.kappa
- Eeeee
- J.Cameron
- Marple
- Kitana
- F1L1PAS
- sophiaa
- VFD59
- papa2g
- το κοριτσι του μαη
- srg96
- Hopeful22
- Φινεύς
- Phys39
- Anta2004
- fairyelly
- Pharmacist01
- jYanniss
- Panagiotis849
- Kokro
- augustine
- Nikoletaant
- Mashiro@Iberan
- margik
- Mammy Nun
- Pastramis
- Σωτηρία
- Appolon
- panosveki
- Nickt23
- igeorgeoikonomo
- Steliosgkougkou
- QWERTY23
- Ameliak
- aladdin
- nimbus
- Φωτεινη Τζα.
- marian
- Georgekk
- xrisamikol
- the purge
- Theodora03
- Machris
- s93060
- Nikitas18
- Stif6
- stav.mdp
- damn
- aekaras 21
- Anthropaki
- Angelos12345
- ioannam
- Μάρκος Βασίλης
- skyway
- Nick2325
- Nala
- Manolo165
- Ryuzaki
- T C
- Devilshjoker
- El_
- George9989
- TonyMontanaEse
- globglogabgalab
- constansn
- barkos
- katerinavld
- fenia
- An_uknown_world
- Jimmis18
- maria2001
- KingPoul
- Xara
- thecrazycretan
- abcdefg12345
- Κλημεντίνη
- ale
- panagiotis G
- mechaniceng
- Giii
- calliope
- Tequila
- natalix
- Cortes
- Alexecon1991
- pepsoula
- Mariaathens
- Lia 2006
- 1205
- παιδι για κλαματα
- Alexandros36k
- alexd99
- chembam
- Specon
- Dr House
- panagiotis23
- Johnman97
- rhymeasylum
- Αννα Τσιτα
- KaterinaL
- Libertus
- LeoDel
- iminspain
- den antexw allh apotyxia
- Λαμπρινηη
- Mendel2003
- Ijt
- drosos
- Κορώνα
- JohnGreek
- Αρχηγος_β3
- alexandra_
- ΘανάσοςG4
- Dimitris9
- Birtjan
- george7cr7
- NickT
- Bgpanos
- JKTHEMAN
- nicole1982
- χημεια4λαιφ
- Stroka
- Kostakis45
- charmander
- leo41
- EiriniS20
- Αριάνα123
- MarilynSt
- iManosX13
- Nefh_
- Viedo
- Βλα
- suaimhneas
- george pol
- kristinbacktoschool
- fearless
- Rene2004
- Steffie88
- Slytherin
- jimnikol21
- Unseen skygge
- cel123
- jul25
- Thanos_D
- Ireneeneri
- tasost
- Mukumbura
- xxxtolis
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki