Μάρκος Βασίλης
Πολύ δραστήριο μέλος
Ο Βασίλης αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 29 ετών, Διδακτορικός και μας γράφει από Καισαριανή (Αττική). Έχει γράψει 1.871 μηνύματα.

10-01-21

12:52
και παλι δεν εχει και πολυ νοημα να ορισεις συναρτηση με ενα σημειο και να πεις ειναι 1 1.μπορει με ενα σημειο να μην ειναι και η fχ= c και να ναι ο θεος ο ιδιος.λογικα ειναι λαθος η προταση.
[automerge]1610275025[/automerge]
Πλακα στην πλακα το οριο που εβαλες δεν εχει νοημα να το ψαξουμε διοτι το πεδιο ορισμου ειναι ενωση μειον απειρο,-1 1, συν απειρο οποτε δεν παει κοντα στο 0.απο την αλλη αν παρεις το οριο του υποριζου ειναι μηδεν.τρεχα γυρευε δηλαδη.οσο για τη συνεχεια λες οτι υπαρχει προβλημα στο κομματι ενωσης?
Τυπικά, η μοναδική συνάρτηση που υπάρχει π.χ. από το {4} στο {7} είναι 1-1, αλλά είναι τετριμμένο παράδειγμα. Είναι, ουσιαστικά, μία ειδική περίπτωση της πρότασης ότι αν έχεις μία συνάρτηση f με πεδίο ορισμού Α και πεδίο τιμών Β, όπου Α και Β πεπερασμένα, τότε αν ισχύουν δύο από τα ακόλουθα τρία, ισχύει και το τρίτο:
- f 1-1,
- f επί,
- |Α|=|Β|.
Με αυτό κατά νου, σε επίπεδο εξετάσεων θεωρώ αδόκιμα τα μονοσύνολα και, γενικότερα, τα πεπερασμένα σύνολα στα πεδία ορισμού συναρτήσεων. Μέσα στην τάξη έχουν σίγουρα αξία, αλλά κι εκεί... πεπερασμένη. :Ρ
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.965 μηνύματα.

10-01-21

12:57
ωπα στο πεδιο ορισμου της περιλαμβανεται και το μηδεν και η ιδιαιτεροτητα ειναι εκει.αν δεν υπηρχε το μηδεν μπορουσες να πεις οτι ειναι στην ενωση.για θυμησε μου με το μηδεν μεσα πως αποδεικνυεις οτι ειναι συνεχης παντου.το θεωρημα με τον πληθαρισμο και f και 1-1 απο θεωρια συνολων σωστος!!Τυπικά, η μοναδική συνάρτηση που υπάρχει π.χ. από το {4} στο {7} είναι 1-1, αλλά είναι τετριμμένο παράδειγμα. Είναι, ουσιαστικά, μία ειδική περίπτωση της πρότασης ότι αν έχεις μία συνάρτηση f με πεδίο ορισμού Α και πεδίο τιμών Β, όπου Α και Β πεπερασμένα, τότε αν ισχύουν δύο από τα ακόλουθα τρία, ισχύει και το τρίτο:
Τώρα, για το όριο, εξ ορισμού, όπως λες, δεν έχει νόημα, καθώς δεν ορίζεται σε περιοχή του μηδενός. Ωστόσο, με τον επίσημο ορισμό, η συνάρτηση είναι συνεχής, ενώ με τον λυκειακό, όχι. Αυτό γίνεται γιατί στο λύκειο η συνέχεια ορίζεται μέσω ορίων, άρα θες να έχεις σημεία συσσώρευσης του πεδίου ορισμού για να είναι μία συνάρτηση συνεχής εκεί.
- f 1-1,
- f επί,
- |Α|=|Β|.
Με αυτό κατά νου, σε επίπεδο εξετάσεων θεωρώ αδόκιμα τα μονοσύνολα και, γενικότερα, τα πεπερασμένα σύνολα στα πεδία ορισμού συναρτήσεων. Μέσα στην τάξη έχουν σίγουρα αξία, αλλά κι εκεί... πεπερασμένη. :Ρ
[automerge]1610276356[/automerge]
παντως για να μην φρικαρουν οι υποψηφιοι δεν μπορει να τεθει ποτε κατι τετοιο.
Μάρκος Βασίλης
Πολύ δραστήριο μέλος
Ο Βασίλης αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 29 ετών, Διδακτορικός και μας γράφει από Καισαριανή (Αττική). Έχει γράψει 1.871 μηνύματα.

10-01-21

16:28
ωπα στο πεδιο ορισμου της περιλαμβανεται και το μηδεν και η ιδιαιτεροτητα ειναι εκει.αν δεν υπηρχε το μηδεν μπορουσες να πεις οτι ειναι στην ενωση.για θυμησε μου με το μηδεν μεσα πως αποδεικνυεις οτι ειναι συνεχης παντου.το θεωρημα με τον πληθαρισμο και f και 1-1 απο θεωρια συνολων σωστος!!
[automerge]1610276356[/automerge]
παντως για να μην φρικαρουν οι υποψηφιοι δεν μπορει να τεθει ποτε κατι τετοιο.
Ο ε-δ ορισμός της συνέχειας πιάνει και τα απομονωμένα σημεία του πεδίου ορισμού, οπότε η συνάρτηση είναι συνεχής στο 0 - παίρνεις δ=1/2 πάντα. Αλλά με την ύλη του λυκείου δεν έχει νόημα να μιλήσουμε για συνέχεια στο 0 γιατί δεν είναι σημείο συσσώρευσης.
ιωαννηs
Επιφανές μέλος
Ο ιωαννηs αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 25 ετών, Φοιτητής του τμήματος Πρόγραμμα Ιερατικών Σπουδών και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 15.428 μηνύματα.

10-01-21

18:16
Πολυ ωραια η δουλεια σου στο βιβλιο Βασιλη ,συγχαρητηρια.Ναι, έχεις δίκιο, είναι και στις οδηγίες του ΙΕΠ αυτό - αλλά και στο σχολικό βιβλίο. Όσες συναρτήσεις εξετάζονται έχουν ως πεδίο ορισμού διάστημα ή ένωση διαστημάτων.
Από την άλλη, {5}=[5,5], οπότε δεν είναι και εκτός ύλης.
Στο μεταίχμιο της ύλης είναι και ο υπολογισμός του ορίου:
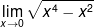
όπως και η συνέχεια της εν λόγω συνάρτησης στο πεδίο ορισμού της - στα πλαίσια της ύλης του λυκείου κ.λπ.
Σε άλλα νέα, επισυνάπτω και λίγες πρόχειρες σημειώσεις και ασκήσεις στην παράγωγο, μιας και ούτε φέτος θα δούμε ολοκληρώματα στις εξετάσεις. Για περισσότερα: aftermathsgr.wordpress.com.
Alexandros28
Δραστήριο μέλος
Ο Alexandros28 αυτή τη στιγμή δεν είναι συνδεδεμένος. Έχει γράψει 750 μηνύματα.

10-01-21

18:25
Αυτό θα λεγα και εγώ. Ευχάριστο για ανάγνωση ακόμα και στον ελεύθερο χρόνο.Πολυ ωραια η δουλεια σου στο βιβλιο Βασιλη ,συγχαρητηρια.
Μάρκος Βασίλης
Πολύ δραστήριο μέλος
Ο Βασίλης αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 29 ετών, Διδακτορικός και μας γράφει από Καισαριανή (Αττική). Έχει γράψει 1.871 μηνύματα.

10-01-21

22:45
Lancelot
Περιβόητο μέλος
Ο Lancelot αυτή τη στιγμή δεν είναι συνδεδεμένος. Έχει γράψει 5.452 μηνύματα.

10-01-21

23:01
Πολύ καλή δουλειά. Η μορφή που προβάλλονται οι άλυτες μου θυμίζει το βιβλίο του Thomas : Απειροστικό ΛογισμόΝαι, έχεις δίκιο, είναι και στις οδηγίες του ΙΕΠ αυτό - αλλά και στο σχολικό βιβλίο. Όσες συναρτήσεις εξετάζονται έχουν ως πεδίο ορισμού διάστημα ή ένωση διαστημάτων.
Από την άλλη, {5}=[5,5], οπότε δεν είναι και εκτός ύλης.
Στο μεταίχμιο της ύλης είναι και ο υπολογισμός του ορίου:
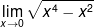
όπως και η συνέχεια της εν λόγω συνάρτησης στο πεδίο ορισμού της - στα πλαίσια της ύλης του λυκείου κ.λπ.
Σε άλλα νέα, επισυνάπτω και λίγες πρόχειρες σημειώσεις και ασκήσεις στην παράγωγο, μιας και ούτε φέτος θα δούμε ολοκληρώματα στις εξετάσεις. Για περισσότερα: aftermathsgr.wordpress.com.
ΥΓ : Θα επεκτείνεις τις σημειώσεις και για πανεπιστημιακά μαθήματα ;
SlimShady
Πολύ δραστήριο μέλος
Ο Κωνσταντίνος αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 21 ετών, Φοιτητής του τμήματος Νομικής ΕΚΠΑ και μας γράφει από Μελίσσια (Αττική). Έχει γράψει 963 μηνύματα.

17-01-21

16:01
Καλησπέρα παιδιά! Μια γνώμη θα ήθελα, για το κατά πόσο είναι σωστή η επίλυσή μου
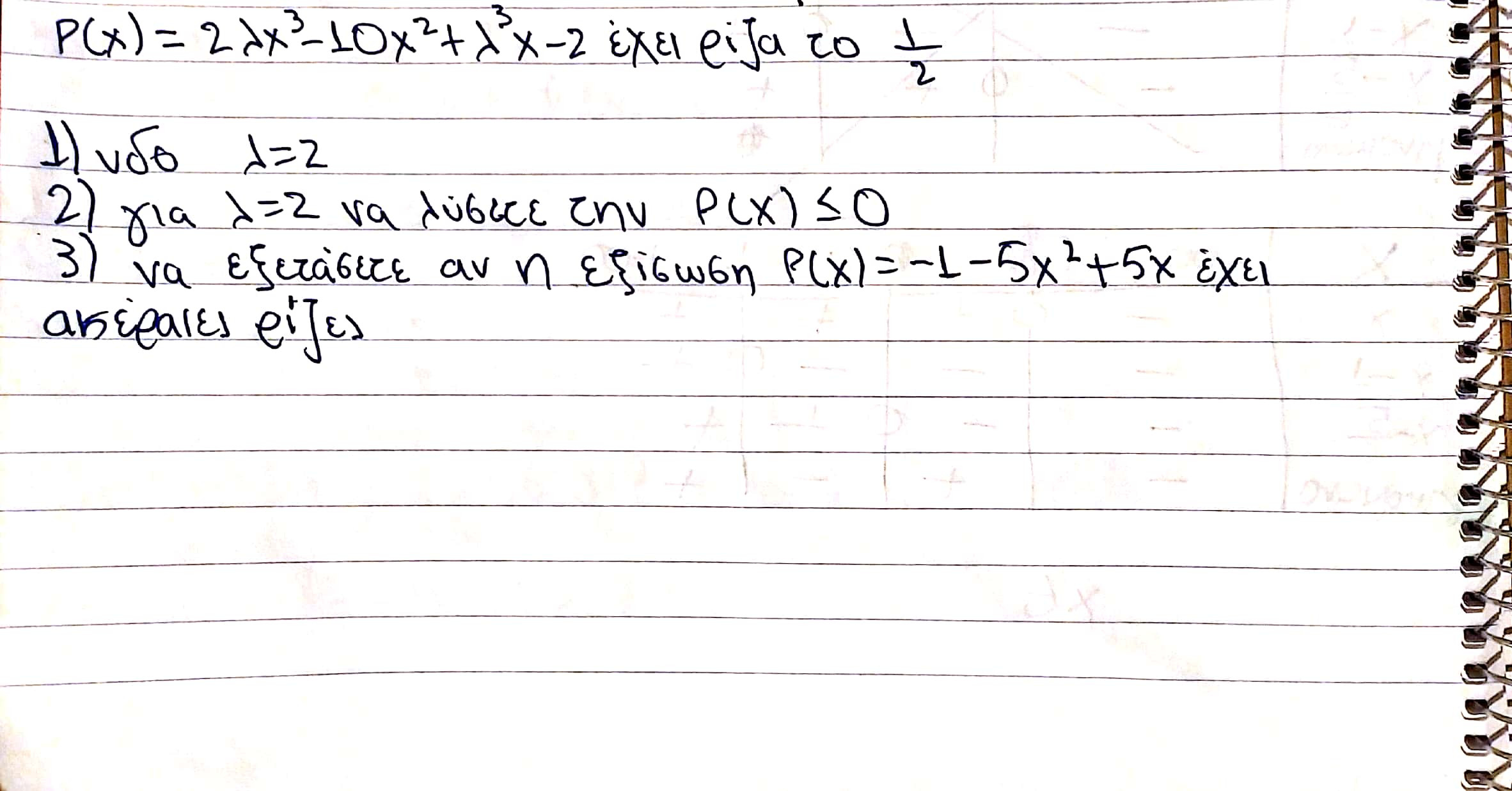
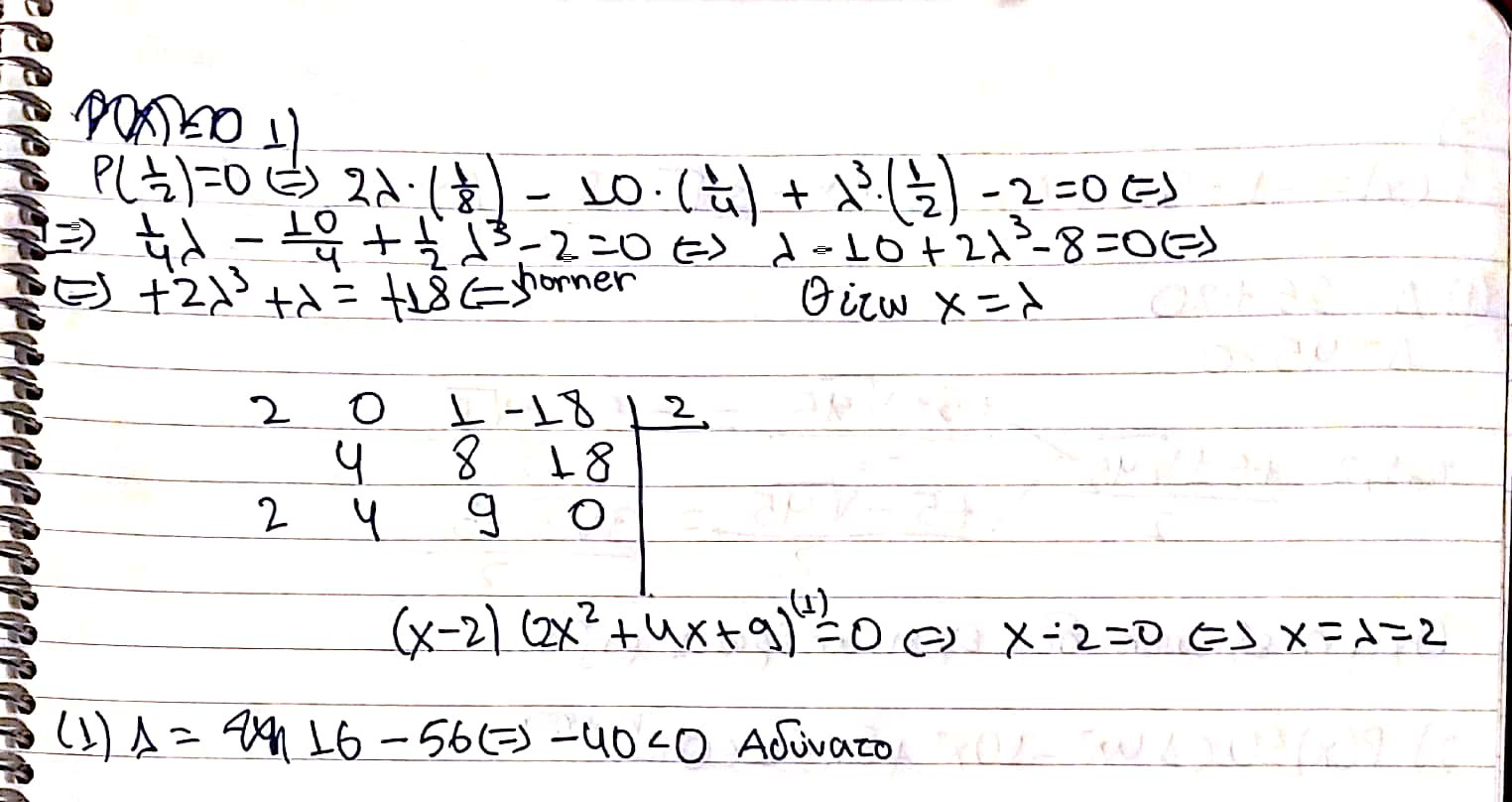

Alexandros28
Δραστήριο μέλος
Ο Alexandros28 αυτή τη στιγμή δεν είναι συνδεδεμένος. Έχει γράψει 750 μηνύματα.

17-01-21

17:08
Δείχνοντας ότι το 2ο μέλος μηδενίζεται για χ που δεν είναι ακέραια δεν εξασφαλίζει σε καμία περίπτωση ότι η εξισωση δεν έχει κάποια ακέραια ριζα. Φέρτα όλα στο πρώτο μέλος και κάνε Horner για όλες τις πιθανές ακέραιες ρίζες. Στο 2 έχεις βρει λάθος τις λυσεις του τριωνυμου. Θα πρεπε να είχες υποπτευτεί ότι έχεις κάνει κάτι λάθος που δε βρήκες σαν ριζα το 1/2 που το δίνει η υπόθεση.
SlimShady
Πολύ δραστήριο μέλος
Ο Κωνσταντίνος αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 21 ετών, Φοιτητής του τμήματος Νομικής ΕΚΠΑ και μας γράφει από Μελίσσια (Αττική). Έχει γράψει 963 μηνύματα.

17-01-21

17:17
Θα μπορουσες να μου εξηγησεις το 1ο γραπτα; το δευτερο μισο το καταλαβα για το 4/8 ηταν λαθος απροσεξιας
Alexandros28
Δραστήριο μέλος
Ο Alexandros28 αυτή τη στιγμή δεν είναι συνδεδεμένος. Έχει γράψει 750 μηνύματα.

17-01-21

17:29
Ας πούμε ότι σου δίνεται η εξισωση
x^2-1=x+1
Παρατηρείς ότι αν X=2 το 2ο μέλος βγαίνει 3. Όμως και το 1ο μέλος βγαίνει 3, που σημαίνει ότι το x=2 είναι λύση της εξίσωσης. Δηλαδή η λύση της εξίσωσης δεν ΜΗΔΕΝΙΖΕΙ και τα 2 μέλη, τα ΕΞΙΣΩΝΕΙ. Εσυ παραγοντοποιησες το 2ο μέλος και είδες ότι μηδενίζεται για x που δεν είναι ακέραια, όμως αυτό δε σημαίνει ότι δεν υπάρχει κάποιο ακέραιο x που να εξισώνει τις τιμές των 2 μελών.
Θυμίσου ότι έχεις να λύσεις την
P(x)=-1-5x^2 +5x
Ο τύπος του πολυώνυμου δεν αλλάζει, πρέπει να τον αντικαταστήσεις. Αυτό που πιστεύω είναι ότι μπερδεύτηκες και νόμιζες ότι αλλάζει ο τύπος του P και έδειξες ότι το 2ο μέλος μηδενίζεται για ρητά χ.
Επίσης δεν ξέρω κατά ποσό είναι σωστό που έθεσες το λ=χ στην εξισωση που βγήκε στο α ερώτημα. Υποτίθεται έχεις αντικαταστήσει ήδη το x με την τιμή 1/2. Όπως και να χει ήταν ψιλό ανούσια κίνηση
x^2-1=x+1
Παρατηρείς ότι αν X=2 το 2ο μέλος βγαίνει 3. Όμως και το 1ο μέλος βγαίνει 3, που σημαίνει ότι το x=2 είναι λύση της εξίσωσης. Δηλαδή η λύση της εξίσωσης δεν ΜΗΔΕΝΙΖΕΙ και τα 2 μέλη, τα ΕΞΙΣΩΝΕΙ. Εσυ παραγοντοποιησες το 2ο μέλος και είδες ότι μηδενίζεται για x που δεν είναι ακέραια, όμως αυτό δε σημαίνει ότι δεν υπάρχει κάποιο ακέραιο x που να εξισώνει τις τιμές των 2 μελών.
Θυμίσου ότι έχεις να λύσεις την
P(x)=-1-5x^2 +5x
Ο τύπος του πολυώνυμου δεν αλλάζει, πρέπει να τον αντικαταστήσεις. Αυτό που πιστεύω είναι ότι μπερδεύτηκες και νόμιζες ότι αλλάζει ο τύπος του P και έδειξες ότι το 2ο μέλος μηδενίζεται για ρητά χ.
Επίσης δεν ξέρω κατά ποσό είναι σωστό που έθεσες το λ=χ στην εξισωση που βγήκε στο α ερώτημα. Υποτίθεται έχεις αντικαταστήσει ήδη το x με την τιμή 1/2. Όπως και να χει ήταν ψιλό ανούσια κίνηση
SlimShady
Πολύ δραστήριο μέλος
Ο Κωνσταντίνος αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 21 ετών, Φοιτητής του τμήματος Νομικής ΕΚΠΑ και μας γράφει από Μελίσσια (Αττική). Έχει γράψει 963 μηνύματα.

17-01-21

17:35
Αααααα τωρα καταλαβα. Εκει με το θετω το εκανα επειδη ειχα ξεχασει οτι ειχα λ και εβαλα χ οποτε για να μην τα σβηνω λεω ας θεσω χ=λ ναι ειναι χαζη κινηση και ατοπη εν μερει αλλα δεν ειναι ασκηση διαγωνισματος
ναι ειναι χαζη κινηση και ατοπη εν μερει αλλα δεν ειναι ασκηση διαγωνισματος
ιωαννηs
Επιφανές μέλος
Ο ιωαννηs αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 25 ετών, Φοιτητής του τμήματος Πρόγραμμα Ιερατικών Σπουδών και μας γράφει από Πειραιάς (Αττική). Έχει γράψει 15.428 μηνύματα.

17-01-21

17:57
Νομιζω μια χαρα και λογικα τα εχεις παει. Οκ το 3/4 ειναι 1/2 τυπογραφικο λαθος το εχεις δει ηδη.
Εκει που θα ελεγα κατι ειναι στο πεδιο ορισμου την ανισωσης . Το πινακακι θα εκανα διαφορετικα και το πεδιο ορισμου του χ θα το εβγαζα απο μειον απειρο εως και 1/2 συμπεριλαμβανομενου και ενωση με το 1
Εκει που θα ελεγα κατι ειναι στο πεδιο ορισμου την ανισωσης . Το πινακακι θα εκανα διαφορετικα και το πεδιο ορισμου του χ θα το εβγαζα απο μειον απειρο εως και 1/2 συμπεριλαμβανομενου και ενωση με το 1
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.965 μηνύματα.

18-01-21

17:15
υπαρχει ενα θεωρημα γνωστο ως θεωρημα ακεραιων ριζων που αν παρεις τους διαιρετες του σταθερου ορου ειναι πιθανες ακεραιες ριζες το τονιζω πιθανες.αρα λοιπον αν τα μαζεψουμε ολα στο πρωτο μελος εχουμε
χ^3-5χ^2+3χ-1=0.
θεωρουμε το πολυωνυμο g(x)=x^3-5x^2+3x-1
οι διαιρετες του σταθερου ορου ειναι 1,-1.g(-1) και g(1) διαφορο του μηδενος.
αρα η εξισωση δεν εχει ακεραιες ριζες.
χ^3-5χ^2+3χ-1=0.
θεωρουμε το πολυωνυμο g(x)=x^3-5x^2+3x-1
οι διαιρετες του σταθερου ορου ειναι 1,-1.g(-1) και g(1) διαφορο του μηδενος.
αρα η εξισωση δεν εχει ακεραιες ριζες.
SlimShady
Πολύ δραστήριο μέλος
Ο Κωνσταντίνος αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 21 ετών, Φοιτητής του τμήματος Νομικής ΕΚΠΑ και μας γράφει από Μελίσσια (Αττική). Έχει γράψει 963 μηνύματα.

18-01-21

20:03
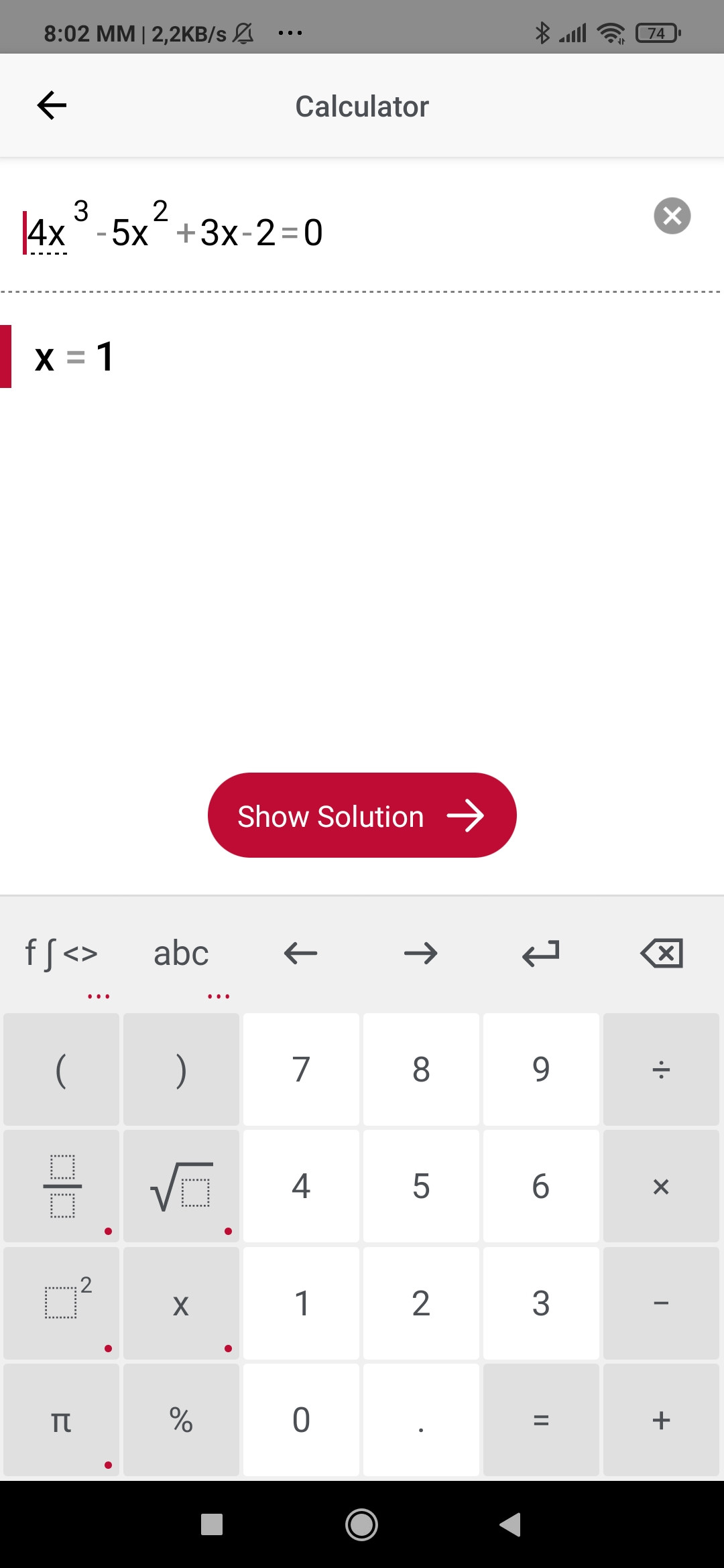
Εμένα βασικά μου βγήκε τόσο
eukleidhs1821
Διάσημο μέλος
Ο eukleidhs1821 αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι Πτυχιούχος του τμήματος Ιατρικής Ιωαννίνων (Ιωάννινα) και μας γράφει από Καινούργιο (Ηράκλειο). Έχει γράψει 3.965 μηνύματα.

18-01-21

20:14
4χ^3-5χ^2+3χ-1=0 αυτο ειναι το σωστο.στο χ^3 o συντελεστης ειναι το 4 οχι ασσος που εβαλα εξαρχης.και παλι δεν αλλαζει το συμπερασμα δεν εχει ακεραιες ριζες
SlimShady
Πολύ δραστήριο μέλος
Ο Κωνσταντίνος αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 21 ετών, Φοιτητής του τμήματος Νομικής ΕΚΠΑ και μας γράφει από Μελίσσια (Αττική). Έχει γράψει 963 μηνύματα.

18-01-21

20:33
Ναι εχεις δικιο
Alexandros28
Δραστήριο μέλος
Ο Alexandros28 αυτή τη στιγμή δεν είναι συνδεδεμένος. Έχει γράψει 750 μηνύματα.

18-01-21

20:35
-2-(-1)=-2+1=-1
SlimShady
Πολύ δραστήριο μέλος
Ο Κωνσταντίνος αυτή τη στιγμή δεν είναι συνδεδεμένος. Είναι 21 ετών, Φοιτητής του τμήματος Νομικής ΕΚΠΑ και μας γράφει από Μελίσσια (Αττική). Έχει γράψει 963 μηνύματα.

18-01-21

20:40
Ναι δεν ειχα δει προηγουμενως σε τι αναφεροταν-2-(-1)=-2+1=-1
Την ασκηση την πηρε σωστη παντως
Alexandros28
Δραστήριο μέλος
Ο Alexandros28 αυτή τη στιγμή δεν είναι συνδεδεμένος. Έχει γράψει 750 μηνύματα.

21-02-21

18:11
Δίνεται συνάρτηση ορισμένη στο IR και δύο φορές παραγωγίσιμη, της οποίας η γραφική παράσταση εφάπτεται στην y=x στο Α(0,f(0)) και ισχύει ότι η δεύτερη παράγωγος της f είναι ίση συνάρτηση με την f. Να βρείτε τον τύπο της f.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 0 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 289 μέλη διάβασαν αυτό το θέμα:
- Maynard
- foxypup
- Pars3c
- mikke
- thepigod762
- 98.8%chimpanzee
- trifasikodiavasma
- ggl
- ioanna2007
- Hased Babis
- Mariosm.
- infection54
- Jesse_
- topg
- eukleidhs1821
- bill09876
- Debugging_Demon
- mali
- Joji
- Ness
- Helen06
- Scandal
- synthnightingale
- arko
- BillyTheKid
- Magigi
- Paragontas7000
- Unboxholics
- just some guy
- george777
- Wonderkid
- Micro
- IceCream05
- Abiogenesis
- GeorgePap2003
- katia.m
- giannhs2001
- paul
- Praxis
- Apocalypse
- shezza94
- desp1naa
- rempelos42
- Sherlockina
- oups
- Dimgeb
- spring day
- KingOfPop
- mpapa
- Chrisa
- Physicsstudent
- tsiobieman
- P.Dam.
- persi
- theodoraooo
- PanosBat
- kost28
- mikriarchitectonissa
- BILL KEXA
- Dr. Gl. Luminous
- Eleftheria2
- Lathy
- bruh_234
- Miranda32
- SlimShady
- kallikd
- nucomer
- alpha.kappa
- Eeeee
- J.Cameron
- Marple
- Kitana
- F1L1PAS
- sophiaa
- VFD59
- papa2g
- το κοριτσι του μαη
- srg96
- Hopeful22
- Φινεύς
- Phys39
- Anta2004
- fairyelly
- Pharmacist01
- jYanniss
- Panagiotis849
- Kokro
- augustine
- Nikoletaant
- Mashiro@Iberan
- margik
- Mammy Nun
- Pastramis
- Σωτηρία
- Appolon
- panosveki
- Nickt23
- igeorgeoikonomo
- Steliosgkougkou
- QWERTY23
- Ameliak
- aladdin
- nimbus
- Φωτεινη Τζα.
- marian
- Georgekk
- xrisamikol
- Poirot
- the purge
- Dora140303
- Machris
- s93060
- Nikitas18
- Stif6
- stav.mdp
- damn
- aekaras 21
- Anthropaki
- Angelos12345
- ioannam
- Μάρκος Βασίλης
- skyway
- Nick2325
- Nala
- Manolo165
- Ryuzaki
- T C
- Devilshjoker
- El_
- George9989
- TonyMontanaEse
- globglogabgalab
- constansn
- barkos
- katerinavld
- fenia
- An_uknown_world
- Jimmis18
- maria2001
- KingPoul
- Xara
- thecrazycretan
- abcdefg12345
- Κλημεντίνη
- ale
- panagiotis G
- mechaniceng
- Giii
- calliope
- Tequila
- natalix
- Ουριήλ
- Cortes
- Alexecon1991
- pepsoula
- Mariaathens
- Lia 2006
- 1205
- παιδι για κλαματα
- Alexandros36k
- alexd99
- chembam
- Specon
- Dr House
- panagiotis23
- Johnman97
- rhymeasylum
- Αννα Τσιτα
- KaterinaL
- Libertus
- LeoDel
- iminspain
- den antexw allh apotyxia
- Λαμπρινηη
- Mendel2003
- Ijt
- drosos
- Κορώνα
- JohnGreek
- Αρχηγος_β3
- alexandra_
- ΘανάσοςG4
- Dimitris9
- Birtjan
- george7cr7
- NickT
- Bgpanos
- JKTHEMAN
- nicole1982
- χημεια4λαιφ
- Stroka
- Kostakis45
- charmander
- leo41
- EiriniS20
- Αριάνα123
- MarilynSt
- iManosX13
- Nefh_
- Viedo
- Βλα
- suaimhneas
- george pol
- kristinbacktoschool
- fearless
- Rene2004
- Steffie88
- Slytherin
- jimnikol21
- Unseen skygge
- cel123
- jul25
- Thanos_D
- Ireneeneri
- tasost
- Mukumbura
- xxxtolis
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki




