Guest 856924
Επισκέπτης


Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Filippos14
Εκκολαπτόμενο μέλος


πιο πολλυ στα αλλα στο τελος εχω ενα θεματακι με τα γεωμετρικα ας πουμε
ευθειες,κον τομες.
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Guest 856924
Επισκέπτης


πως γινεται αυτη η προοδος?
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
pkat876
Εκκολαπτόμενο μέλος


αν z^2004=1 τοτε |1+z+z^2+...z^2002|=1 με z#1
πως γινεται αυτη η προοδος?
Δεν βγαίνει και μ' έχει εκνευρίσει πολύυυυ


Λοιπόν...
Καταρχάς η πρόοδος είναι γεωμετρική.
Έχουμε α1=1 (z^0) και λ=z
S2002=z^2002 -1/ z-1
και καταλήγω σε S2002= -(1+z)/z2 ( αντικατέστησα το z^2002=z^2004*z^-2)
Παίρνω το μέτρο του και καταλήγω σε βλακείες με χ,ψ!!!
Είναι σωστή η λογική μου αρχικά;;;


Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


αν z^2004=1 τοτε |1+z+z^2+...z^2002|=1 με z#1
πως γινεται αυτη η προοδος?
και το μόνο που μένει είναι να δείξουμε ότι
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Guest 856924
Επισκέπτης


Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
pkat876
Εκκολαπτόμενο μέλος


και το μόνο που μένει είναι να δείξουμε ότι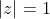
Δεν χρειάζεται το τελευταίο =!!! Κάνοντας ομώνυμα και βγάζοντας κοινό παράγοντα το z βγαίνει |-1|=1!!!



Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Guest 856924
Επισκέπτης


Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
pkat876
Εκκολαπτόμενο μέλος


πως δειχνω οτι αυτη η σχεση δεν εχει πραγματικη ριζα? |1+iz|^1995=1
Μήπως δίνει ότι ο z είναι μη μηδενικός; Γιατί δεν βγαίνει....

Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Vold
Πολύ δραστήριο μέλος


Κάνεις τις πράξεις και καταλήγεις σε μια σχέση της μορφής x^2 + (y-1)^2=1
Έστω ότι η σχέση δεν έχει πραγματικές ρίζες: Θα πρέπει το x να είναι μηδέν, άρα (y-1)^2=1 δηλαδή y=2
Έστω ότι η σχέση έχει πραγματικές ρίζες: Θα πρέπει το y να είναι μηδέν, άρα x^2 + 1 = 1 άτοπο αφού το x είναι διάφορο του μηδενός...
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
blackorgrey
Εκκολαπτόμενο μέλος


Λές ότι έστω ότι έχει πραγματική ρίζαπως δειχνω οτι αυτη η σχεση δεν εχει πραγματικη ριζα? |1+iz|^1995=1




Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Διονύσης13
Τιμώμενο Μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
pkat876
Εκκολαπτόμενο μέλος


Συνοπτικά: Καταλήγουμε αντικαθιστώντας με Ζ=χ+ψi στην αρχική εξίσωση στη σχέση (1-ψ)^2 +x^2=1 (1)
Έστω ότι η εξίσωση δεν έχει πραγματική ρίζα άρα ζητάω ψ=0
Από (1) καταλήγουμε σε ψ=0 (εδώ κολλάει ότι ο ζ είναι μη μηδενικός
 )
)Άρα άτοπο
Έχει λοιπόν πραγματικές ρίζες Άρα ζητάω χ=0
Οπότε (1-ψ)^2=1
|1-ψ|=1
ψ=2 ή ψ=0(απορ)
Άρα Ζ=2i μοναδική ρίζα της εξίσωσης!
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Guest 856924
Επισκέπτης


ετσι οπως στο δινω ειναιΜήπως δίνει ότι ο z είναι μη μηδενικός; Γιατί δεν βγαίνει....
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
pkat876
Εκκολαπτόμενο μέλος


ετσι οπως στο δινω ειναι
ΟΚ Θα ρωτήσω και την καθηγήτριά μου στο φροντιστήριο...
 Είναι από βοήθημα η άσκηση;
Είναι από βοήθημα η άσκηση;Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος


πως δειχνω οτι αυτη η σχεση δεν εχει πραγματικη ριζα? |1+iz|^1995=1
Θέτουμε z=x+yi όπου x,y πραγματικοί αριθμοί. Έχουμε:
1+zi=1+(x+yi)I=1+xi+y*(i^2)=1+xi+y*(-1)=1+xi-y=(1-y)+xi
|1+iz|=SQRT[((1-y)^2)+(x^2)]=SQRT[(x^2)+((y-1)^2)]
|1+iz|^1995=1 => |1+iz|=1 => |1+iz|^2=1 => (x^2)+((y-1)^2)=1
Επομένως η εικόνα του z ανήκει σε κύκλο με κέτρο Κ(0,1) και ακτίνα ρ=1. Οι παραμετρικές εξισώσεις αυτού του κύκλου είναι:
x=συνθ
y=1+ημθ
0<=θ<2π
Άρα οι λύσεις της εξίσωσης |1+iz|^1995=1 είναι οι μιγαδικοί αριθμοί z με
z=συνθ+(1+ημθ)i
όπου 0<=θ<2π
Για να είναι ο z πραγματικός αριθμός, πρέπει να ισχύει y=0. Έχουμε:
1+ημθ=0 => ημθ=-1 => θ=3π/2 καθώς 0<=θ<2π
Για θ=3π/2 είναι ημθ=-1 και συνθ=0
Συνεπώς
x=συνθ=0
y=1+ημθ=0
Άρα η μοναδική πραγματική ρίζα της εξίσωσης |1+iz|^1995=1 είναι ο αριθμός z=0.
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Guest 856924
Επισκέπτης


απ του φροντιστηριουΟΚ Θα ρωτήσω και την καθηγήτριά μου στο φροντιστήριο...Είναι από βοήθημα η άσκηση;
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Fedde le Grand
Πολύ δραστήριο μέλος


Δυσκολευομαι στις ασκησεις γεωμετρικων τοπων και σε καποιες με μετρα... (για μιγαδικους μιλαω παντα)..
Τι να κανω? τι προτεινετε?
Αρχικά, κάνε μια καλή επανάληψη τα Μαθηματικά Κατεύθυνσης της Β΄. Από εκεί και πέρα, τι είναι αυτό που σε δυσκολεύει συγκεκριμένα; Τη θεωρία τη ξέρεις πολύ καλά; Ακόμη, να έχεις υπόψιν ότι στις ασκήσεις με μέτρα μπορείς να υψώσεις στο τετράγωνο και τα δύο μέλη και να εφαρμόσεις ιδιότητα ζ (επί) ζσυζυγής, πράξεις και βγαίνει. Είναι κάποια στάνταρ πραγματάκια τα οποία πολλές φορές μας λύνουν τα χέρια. Θα σου στείλω και ένα ΠΜ με ένα link που ίσως σε βοηθήσει

ΥΓ: Τώρα είδα ότι είναι παλιό το μήνυμα...
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Guest 856924
Επισκέπτης


πως δειχνουμε οτι το |z|=1 ?
και το μόνο που μένει είναι να δείξουμε ότι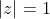
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος


πως δειχνουμε οτι το |z|=1 ?
z^2004=1 => |z^2004|=|1| => |z|^2004=1 => |z|=1
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 2 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 227 μέλη διάβασαν αυτό το θέμα:
- hristosdab
- trifasikodiavasma
- haji
- thepigod762
- Mariosm.
- soulatso
- oteletampis
- phleidhs
- Hased Babis
- AggelikiGr
- sir ImPeCaBlE
- veiNqh
- Scandal
- alekos
- Debugging_Demon
- just some guy
- xristosgkm
- ismember
- Apocalypse
- arrow25
- rempelos42
- ggl
- GStef
- QWERTY23
- xrisamikol
- Σωτηρία
- nikoletaz57
- _Aggelos123
- Mariam38
- SlimShady
- strsismos88
- Georgekk
- Lia 2006
- igeorgeoikonomo
- marian
- tsiobieman
- constansn
- Xristosdimitra
- Panagiotis849
- ρενακι 13
- Memetchi
- eukleidhs1821
- Nikkkpat
- Unboxholics
- korlef
- kwstaseL
- Thanos_D
- the purge
- T C
- Giii
- Papachrist
- liaiscool
- Αννα Τσιτα
- globglogabgalab
- Pharmacist01
- thanahss
- abcdefg12345
- nicole1982
- thecrazycretan
- kvstas92
- KingOfPop
- maria301
- papa2g
- stefan
- Κλημεντίνη
- TonyMontanaEse
- Athens2002
- Alexecon1991
- Μάρκος Βασίλης
- Cortes
- το κοριτσι του μαη
- calliope
- ale
- panagiotis G
- Kleanth
- aggelosst9
- BioChemical
- spring day
- nucomer
- Georgia110
- LeoDel
- pink_panther
- Alexandros973
- marsenis
- den antexw allh apotyxia
- KaterinaL
- kiyoshi
- drosos
- Λαμπρινηη
- Bill22
- Chrysablac.
- giorgosp97
- Βλα
- Monster Hunter
- jul25
- xxxtolis
- Stroka
- nicks1999
- totiloz
- Earendil
- mitsakos
- tasost
- lnesb
- ssalex
- Vasilina93
- alan09
- Livaja10
- χημεια4λαιφ
- Viedo
- UncleJ
- Kostakis45
- Infrared
- Zgian
- pepatogourounaki
- hirasawayui
- GeoCommand
- Eleni54
- American Economist
- EiriniS20
- ΘανάσοςG4
- stamoul1s
- Αριάνα123
- uni77
- Libertus
- tasoss
- PanosCh002
- Unseen skygge
- Νικόλας Ραπ.
- cel123
- The Limit Does Not Exist
- don_vito
- suaimhneas
- Αλκης Κ.
- alexrami
- Baggelitsa36
- Νομικάριος13
- spinalgr1990
- d_th
- Adolfo valencia
- Πα.Κ
- Vasilis25
- Johnman97
- Steffie88
- rekcoR
- gwgw_5
- fockos
- Mariahj
- roud
- kostas83
- Cpt.Philips
- Makis45
- Χρησλου
- Panos_02
- Vold
- tymvorixos
- GiorgosAsi
- Neos167
- theodoraooo
- George187
- Άρτεμις Α.
- Μαρία2222
- christos87
- Idontknoww
- jimis2001
- Metamorph
- Γατόπαρδος.
- Johnsk
- mitsos14
- johnsiak
- Elel
- Dreamer_SW
- Γιαννης1987Θεσσ
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki

