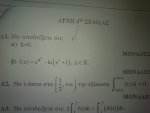Guest 856924
Επισκέπτης


Βρειτε την μονοτονια τον f,g
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Α.δινεται f(x)=(2x-1)^2+|z+xw|,x E R z,w E C και μη μηδενικοι μιγαδικοι ανεξαρτητοι του χ και |z|=1 Επισης ισχυει z^5 + 2(z^4)w-z+w=0 και 2z+w διαφορο του μηδενος.
Αα)ν.α.ο |z+2w|=|z-w|
Aβ)|z+xw| διαφορο του μηδενος για καθε χ Ε R kαι |z+xw|={(|w|^2)x^2+2Re(zwσυζηγης)χ+1}^(1/2)
γ)υπαρχει ενα τουλαχιστον ξΕ(-1,2) ωστε
|w|^2 ξ+Re(z wσυζηγης)=(4-8ξ)|z+ξw|
Β)Αν |w|=1 να εκφρασετε την f(x) χωρις μιγαδικους και να βρειτε το ελαχιστο της
α)
β)
Για
Aντικαθιστώντας στην (1) παίρνουμε:
όμως
λόγω υπόθεσης, άτοπο. Άρα
γ)
Είναι
οπότε αν θεωρήσουμε τη συνεχή συνάρτηση
και από Βοlzano
Β.
Η
με πεδίο ορισμού
Οι συναρτήσεις
Οι συναρτήσεις
Τελικά
οπότε η
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
meletis96
Νεοφερμένο μέλος


Nα βρέιτε 2 μιγαδικούς z1 ,z2 των οποίων οι εικόνες βρίσκονται πάνω στις ευθείες με εξισώσεις ε1: ψ=χ+3 και ε2: ψ=-χ+1 αντλιστοιχα , ώστε να ισχύει z=z1-2z2
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
jasonosaj
Νεοφερμένο μέλος


Δίνεται μιγαδικός αριθμός z=1+i
Nα βρέιτε 2 μιγαδικούς z1 ,z2 των οποίων οι εικόνες βρίσκονται πάνω στις ευθείες με εξισώσεις ε1: ψ=χ+3 και ε2: ψ=-χ+1 αντλιστοιχα , ώστε να ισχύει z=z1-2z2
εστω ℤ1=a+bi
και ℤ2=g+di
πρεπει
ℤ=ℤ1-2ℤ2
ℤ=a+bi-2g-2di
ℤ=(a-2g)+(b-2d)i
ομως ℤ=1+1i
αρα πρεπει
a-2g=1 (1)
b-2d=1 (2)
ℤ1ε (ε)1 y=x+3 άρα b=a+3 (3)
ℤ2ε (ε)2 y=-x+1 άρα d=-g+1 ⇔ g=1-d (4)
απο τις (1),(2),(3),(4) έχουμε
a-2g=1⇔b-3-2g=1⇔b-2g=4 (5)
b-2d=1⇔b-2(-g+1)=1⇔b+2g-1=1⇔b+2g=2 (6)
αθροίζοντας κατα μελη τις (5) (6) βρισκουμε a=0,b=3,g=-1/2,d=3/2
δεν ξερω αν ειναι σωστη η λυση μου

Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
nikoslarissa
Δραστήριο μέλος


Στους μαθηματικούς διαγωνισμούς έχουν νόημα οι ρίζες αρνητικού αριθμού.Εννοείται όταν είναι περιττού βαθμού.Προσωπικά, δεν με ενοχλεί να δω γραμμένη κυβικη ρίζα αρνητικού αριθμού. Όμως υπάρχει ένας (χαζός) κανόνας που λέει ότι κάτω από ρίζα μπαίνουν μόνο θετικοί (ή έστω μηδενικοί) αριθμοί.
Παράδειγμα:
Ηδίνει λύση στο σύνολο των πραγματικών, αλλά είναι λάθος σαν έκφραση.
Ηδίνει λύση +/-2i, στο σύνολο των μιγαδικών, αλλά είναι λάθος σαν έκφραση.
Παρόλο που υπάρχουν ρίζες αρνητικών αριθμών, θεωρείται λάθος να το γράψεις...
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Filippos14
Εκκολαπτόμενο μέλος


Ειναι f(0)=-1 και f(x0)=0 . Oμως x0<0 και ισχυει -1<0 <=> f(0)<f(x0) και εφοσον ειναι γνησια μονοτονη κλπ κλπ,ξερειςΑν f,g:R--->R γνησιως μονοτονες με την Cf να τεμνει τον αρνητικο ημιαξονα ΟΧ' και τον αξονα Υ΄'Υ στο Α(0,-1) και την Cg να τεμνει τον θετικο ημιαξονα ΟY και τον χ'χ στο -1
Βρειτε την μονοτονια τον f,g

Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Guest 856924
Επισκέπτης


δε πολυκαταλαβαΕιναι f(0)=-1 και f(x0)=0 . Oμως x0<0 και ισχυει -1<0 <=> f(0)<f(x0) και εφοσον ειναι γνησια μονοτονη κλπ κλπ,ξερεις
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Filippos14
Εκκολαπτόμενο μέλος


Αν f ειναι γνησια μονοτονη,δηλαδη διατηρει παντου το ιδιο ειδος μονοτονιας,για την βρουμε αρκει να βρουμε μια διαταξη που ισχυει για 2 χ1,χ2 και f(x1),f(x2).δε πολυκαταλαβα
Αν ισχυει χ1>χ2 και f(x1)>f(x2) τοτε ειναι γνησια αυυουσα.
Αν ομως ισχυει x1>x2 και βρουμε καπως οτι f(x1)<f(x2) τοτε ειναι γνησια φθινουσα.
Να στο πω απλα οπως το καταλαβαινω:Αν αλλαζει η φορα πηγαινοντας απο x1,x2 σε αντιστοιχες τιμες ειναι φθινουσα,αν διατηρει την φορα τοτε ειναι αυξουσα.(ΟΜΩς ΠΡΕΠΕΙ ΝΑ ΓΝΩΡΙΖΕΙς ΟΤΙ ΕΙΝΑΙ ΓΝΗΣΙΑ ΜΟΝΟΤΟΝΗ
) διαφορετικα δεν ισχυει τπτ απο τα παραπανω !.
Π.Χ Γνωριζουμε οτι 0>1 , αν με καποια πληροφορια καταληξουμε οτι f(0)>f(1) τοτε η f ειναι γνησιως αυξουσα (στο διαστημα π ειναι γνησιως μονοτονη,εκει που διατηρει μονοτονια,δηλαδη η μονο θα ανεβαινει γραφικα,η θα κατεβαινει).
Οτι αλλο θες πες

P.S: Εισαι δευτερα και χαλας την καλυτερη περιοδο της χρονιας για να λυνεις ασκησεις γ λυκειου?Ανοιξε και πεξε κανα lol/dota κλπ .Θα σου λειψουν του χρονου

Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Guest 856924
Επισκέπτης


Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
DumeNuke
Τιμώμενο Μέλος


Αν f,g:R--->R γνησιως μονοτονες με την Cf να τεμνει τον αρνητικο ημιαξονα ΟΧ' και τον αξονα Υ΄'Υ στο Α(0,-1) και την Cg να τεμνει τον θετικο ημιαξονα ΟY και τον χ'χ στο -1
Βρειτε την μονοτονια τον f,g
Άρα, υπάρχει x1<0 : f(x1)=0Cf να τεμνει τον αρνητικο ημιαξονα ΟΧ'
Άρα, υπάρχει x2=0 : f(x2)=-1<0Α(0,-1)
Επομένως, συναρτήσει όσων είπε ο φίλιππος:
Για x1<x2 => f(x1)>f(x2) και η f είναι γνησίως μονότονη. Άρα είναι γνησίως φθίνουσα. Με τον ίδιο τρόπο βγάζεις τη μονοτονία της g.
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Silent_Killer
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Συνημμένα
methexys
Τιμώμενο Μέλος


Δ2: αφού το ολοκληρώμα κάνει μηδέν, αν η μέσα συνάρτηση f διατηρεί πρόσημο, τότε τα άκρα του ολοκληρώματα είναι ίσα, δηλαδή G(x)=xF(x) (αυτό θέλει απόδειξη όμως). Οπότε μετα δοκιμαζεις τους κλασικούς τρόπους για να τη λύσεις..
Δ3: φέρε το ολοκληρώμα μπροστά, θεώρησε καμια συνάρτηση, γενικά "παιξτο" λίγο και θα σου βγει λογικά, δεν βλέπω τη λύση τώρα, αλλά κατι τέτοιο θα θέλει και φρόντισε να αξιοποιήσεις τα δεδομένα.
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Silent_Killer
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
DumeNuke
Τιμώμενο Μέλος


μπορειτε να με βοηθησετε στα δ2,3 ; πως λυνονται τετοιες ασκησεις; υπαρχει μεθολογια;
Δ2: Αφού φτάσεις στο G(x)=xF(x), φέρτα μπροστά και δώσε όνομα. Η συνάρτηση k(x)=G(x)-xF(x) θα σου βγει γνησίως φθίνουσα. Υπάρχει προφανής ρίζα της k(x) η οποία, λόγω μονοτονίας, είναι μοναδική.
Δ3: Χρησιμοποιώντας τη μονοτονία της k(x) και τη ρίζα της, βρίσκεις ότι k(x)<0 για x>1/2. Αντικαθιστάς, στην k(x), όπου χ το 2 και βγαίνει η ανίσωση.
Την μεθοδολογία στο Δ2 στην έδωσε η methexys.
Στο Δ3 διακρίνονται δύο περιπτώσεις. Και στις δυο προσπαθείς να δημιουργήσεις γνωστές συναρτήσεις:
α) Το tf(t)dt σου δίνει την G(x) και το f(t)dt την F(x). Αλλά σου τα χαλάει το 2, το οποίο "τυχγάνει" να είναι το πάνω άκρο ολοκλήρωσης, και στην G και την F. Δηλαδή έχεις 2F(2)<G(2), όταν παραπάνω "τυχγάνει" να θέτεις συνάρτηση k(x)=G(x)-xF(x). Δημιουργείς δηλαδή την ανίσωση k(2)<0 ή k(2)<k(1/2). Αυτή η περίπτωση λύνεται με μονοτονία.
β) Στη δεύτερη περίπτωση δημιουργείται ανίσωση της μορφής (πχ): F(3)-F(1)<F(6)-F(4). Σε αυτή την περίπτωση προσπαθείς να προσαρμόσεις του όρους με τρόπο τέτοιο, ώστε αν διαιρέσεις με έναν άριθμο, να θα σου "βγαίνει" την διαφορά των τετμημένων. Εδώ, διαιρείς και τα δύο μέλη με το 2. Στα αριστερά παίρνεις 3-1, στα δεξία 6-4. Δημιούργησες, δηλαδή, ΘΜΤ στα (1,3) και (4,6). Τότε δουλεύεις με κυρτότητα (μονοτονία πρώτης παραγώγου). Συνεπώς F'(1,3)<F'(4,6). Βρισκεις την F κυρτή και λύθηκε (αν την βρεις κοίλη την γ*****ς.
 )
)Συνήθως, το προηγούμενο ερώτημα σε καθοδηγεί σε ποια περίπτωση δουλεύεις. Στο Δ2 δημιούργησες συνάρτηση, την οποία μελέτησες προς την μονοτονία, άρα, πιθανότατα, είσαι στην α) περίπτωση. Η δεύτερη περίπτωση, συνήθως, ζητάει να βρεθεί η κυρτότητα από το προηγούμενο ερώτημα.
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Silent_Killer
Πολύ δραστήριο μέλος
rebel
Πολύ δραστήριο μέλος


και η εξίσωση δεν έχει λύσεις για
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Χαράλαμπος μβ
Νεοφερμένο μέλος


α.νδο
B. υπάρχει μοναδικό
γ. να λύσετε την εξίσωση
δ.να εξετάσετε την
οποιος μπορεί ας βοηθησει στο γ.

Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Για
Αν
Τελικά μοναδική λύση είναι η
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Silent_Killer
Πολύ δραστήριο μέλος


δεν μπορει για αλλο χ διαφορο του 1/2 να ισχύει;Hείναι μία προφανής λύση. Για
είναι
με το ίσον να ισχύει μόνο για
και επίσης
( δεν χρειάζεται μελέτη μονοτονίας, το δίνει στην εκφώνηση). Συνεπώς
και η εξίσωση δεν έχει λύσεις για.
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Filippos14
Εκκολαπτόμενο μέλος


https://lisari.blogspot.com/2014/04/blog-post_7.htmlδεν μπορει για αλλο χ διαφορο του 1/2 να ισχύει;
Σημείωση: Το μήνυμα αυτό γράφτηκε 10 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 4 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 227 μέλη διάβασαν αυτό το θέμα:
- hristosdab
- trifasikodiavasma
- haji
- thepigod762
- Mariosm.
- soulatso
- oteletampis
- phleidhs
- Hased Babis
- AggelikiGr
- sir ImPeCaBlE
- veiNqh
- Scandal
- alekos
- Debugging_Demon
- just some guy
- xristosgkm
- ismember
- Apocalypse
- arrow25
- rempelos42
- ggl
- GStef
- QWERTY23
- xrisamikol
- Σωτηρία
- nikoletaz57
- _Aggelos123
- Mariam38
- SlimShady
- strsismos88
- Georgekk
- Lia 2006
- igeorgeoikonomo
- marian
- tsiobieman
- constansn
- Xristosdimitra
- Panagiotis849
- ρενακι 13
- Memetchi
- eukleidhs1821
- Nikkkpat
- Unboxholics
- korlef
- kwstaseL
- Thanos_D
- the purge
- T C
- Giii
- Papachrist
- liaiscool
- Αννα Τσιτα
- globglogabgalab
- Pharmacist01
- thanahss
- abcdefg12345
- nicole1982
- thecrazycretan
- kvstas92
- KingOfPop
- maria301
- papa2g
- stefan
- Κλημεντίνη
- TonyMontanaEse
- Athens2002
- Alexecon1991
- Μάρκος Βασίλης
- Cortes
- το κοριτσι του μαη
- calliope
- ale
- panagiotis G
- Kleanth
- aggelosst9
- BioChemical
- spring day
- nucomer
- Georgia110
- LeoDel
- pink_panther
- Alexandros973
- marsenis
- den antexw allh apotyxia
- KaterinaL
- kiyoshi
- drosos
- Λαμπρινηη
- Bill22
- Chrysablac.
- giorgosp97
- Βλα
- Monster Hunter
- jul25
- xxxtolis
- Stroka
- nicks1999
- totiloz
- Earendil
- mitsakos
- tasost
- lnesb
- ssalex
- Vasilina93
- alan09
- Livaja10
- χημεια4λαιφ
- Viedo
- UncleJ
- Kostakis45
- Infrared
- Zgian
- pepatogourounaki
- hirasawayui
- GeoCommand
- Eleni54
- American Economist
- EiriniS20
- ΘανάσοςG4
- stamoul1s
- Αριάνα123
- uni77
- Libertus
- tasoss
- PanosCh002
- Unseen skygge
- Νικόλας Ραπ.
- cel123
- The Limit Does Not Exist
- don_vito
- suaimhneas
- Αλκης Κ.
- alexrami
- Baggelitsa36
- Νομικάριος13
- spinalgr1990
- d_th
- Adolfo valencia
- Πα.Κ
- Vasilis25
- Johnman97
- Steffie88
- rekcoR
- gwgw_5
- fockos
- Mariahj
- roud
- kostas83
- Cpt.Philips
- Makis45
- Χρησλου
- Panos_02
- Vold
- tymvorixos
- GiorgosAsi
- Neos167
- theodoraooo
- George187
- Άρτεμις Α.
- Μαρία2222
- christos87
- Idontknoww
- jimis2001
- Metamorph
- Γατόπαρδος.
- Johnsk
- mitsos14
- johnsiak
- Elel
- Dreamer_SW
- Γιαννης1987Θεσσ
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki