Μαριλινάκι
Νεοφερμένο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
DumeNuke
Τιμώμενο Μέλος


Πώς βρίσκω το ολοκλήρωμα της ρίζασ 4-χ εις το τετράγωνο ( μόνο το χ έχει τετράγωνο ) μ άκρα ολοκλήρωσης 0,1 και το ολοκλήρωμα e εις τη χ τετράγωνο με τα ίδια άκρα ολοκλήρωσης?
Πού πήγες και τα βρήκες αυτά? Το Ολοκλήρωμα(e^(x^2)) δεν μπορεί να υπολογιστεί...
Το Ολοκλήρωμα(ρίζα(4-χ^2)) [2asin(x/2)+x/2*ρίζα(4-χ^2)]
ό,τι και αν είναι το asin.
Έγινε διόρθωση.
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Filippos14
Εκκολαπτόμενο μέλος


Μπορείτε να με βοηθήσετε με την παράγουσα της 1: ( 1+ex ) ( 1 προς ένα και ε εις τη χ ) και με τη άσκηση 24 από το β τέυχος του Μπάρλα ( το καινούριο) σελ 401?
Ευχαριστώ
Η ολοκληρο-διαφορικη ειναι λιγο ζορικη,εχει πολλα.Τεσπα την f(x)=1/lnx + c εβγαλα.Δεν βρηκα την σταθερα γιατι τιν εκανα γρηγορα και βαριεμαι κιολας
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος


Πού πήγες και τα βρήκες αυτά? Το Ολοκλήρωμα(e^(x^2)) δεν ορίζεται...
Μην τα λες αυτά γιατί μπερδεύεις τους υποψηφίους.
Η συνάρτηση f(x)=e^(x^2) είναι συνεχής στο R και επομένως ολοκληρώσιμη σε οποιοδήποτε διάστημα [α,β] υποσύνολο του R. Το ότι δεν υπάρχει κλειστή αναλυτική λύση για το αόριστο ολοκλήρωμα της f στο [α,β] είναι άλλο θέμα.
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Capellini
Νεοφερμένο μέλος


Με σειρές δεν λύνεται αυτό;Μην τα λες αυτά γιατί μπερδεύεις τος υποψηφίους.
Η συνάρτηση f(x)=e^(x^2) είναι συνεχής στο R και επομένως ολοκληρώσιμη σε οποιοδήποτε διάστημα [α,β] υποσύνολο του R. Το ότι δεν υπάρχει κλειστή αναλυτική λύση για το αόριστο ολοκλήρωμα της f στο [α,β] είναι άλλο θέμα.
Kαι έχω την εντύπωση ότι ένα ολοκλήρωμα με ίδια άκρα είναι μηδέν ή δεν θυμάμαι καλά ;
Το arccos(x) που έγραψε κάποιος πιο πάνω ισούται με την γωνία που έχει συνημίτονο x
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Guest 018946
Επισκέπτης


Μην τα λες αυτά γιατί μπερδεύεις τος υποψηφίους.
Η συνάρτηση f(x)=e^(x^2) είναι συνεχής στο R και επομένως ολοκληρώσιμη σε οποιοδήποτε διάστημα [α,β] υποσύνολο του R. Το ότι δεν υπάρχει κλειστή αναλυτική λύση για το αόριστο ολοκλήρωμα της f στο [α,β] είναι άλλο θέμα.
για το #7358 ποστ έχεις κάποια άποψη πως μπορεί να προχωρήσει ?
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Mariaal
Εκκολαπτόμενο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
vimaproto
Πολύ δραστήριο μέλος


Πώς βρίσκω το ολοκλήρωμα της ρίζασ 4-χ εις το τετράγωνο ( μόνο το χ έχει τετράγωνο ) μ άκρα ολοκλήρωσης 0,1 και το ολοκλήρωμα e εις τη χ τετράγωνο με τα ίδια άκρα ολοκλήρωσης?
Ονομάζω χ=2ημω ==> dx=2συνωdω
Η ρίζα γίνεται 2συνω και τα όρια αλλάζουν όταν χ=0 και ω=0 ενώ όταν χ=1 ω=π/6
Το ολοκλήρωμα γίνεται (ξέχνα το Latex γιατί ακόμα φορτώνει και έτσι θα σου το περιγράψω) ολοκλ[2συνω.2συνωdω=ολοκλ[4συν²ωdω]=4ολοκλ[((1+συν2ω)/2)dω=(τύπος διπλασίου τόξου)=2ολοκλ[dω]+ολοκλ[συν2ωd(2ω)=2ω+ημ2ω=π/3+ριζα3/2
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
nikoslarissa
Δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Guest 018946
Επισκέπτης


Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
nikoslarissa
Δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Guest 018946
Επισκέπτης


Να βρείτε τον τύπο της παραγωγίσιμης συνάρτησης για την οποία ισχύει
και
για καθε
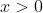
ανταυτου θα σου κάνω μία ερωτηση :
η g(x)=f(x)+xf'(x) είναι η μηδενική ?
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
nikoslarissa
Δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Filippos14
Εκκολαπτόμενο μέλος


Τι εννοεις δεν φαινεται;
Κανε απαλοιφη,βγαινει ταυτοτητα μετα αν τα φερεις μπρωστα ολα.
f(x)= 1/x εβγαλα αλλα μην το δεσεις κομπο γιατι καθως ελυνα ετρωγα.
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
nikoslarissa
Δραστήριο μέλος


Τοσο βγαίνει το έκανα με απαλοιφή βγαίνει g(x)^2=0 με g(x) αυτή που έγραψε ο tasosΚανε απαλοιφη,βγαινει ταυτοτητα μετα αν τα φερεις μπρωστα ολα.
f(x)= 1/x εβγαλα αλλα μην το δεσεις κομπο γιατι καθως ελυνα ετρωγα.
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Filippos14
Εκκολαπτόμενο μέλος


Τοσο βγαίνει το έκανα με απαλοιφή βγαίνει g(x)^2=0 με g(x) αυτή που έγραψε ο tasos
Ωραια και εγω ετσι το βγαλα.

Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Lost in the Fog
Νεοφερμένο μέλος
DumeNuke
Τιμώμενο Μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος


μια βοηθεια στις παρακατω ασκησεις...
2η άσκηση
α) Η f έχει πεδίο τιμών το f(R)=R και ισχύει 3f(x)+συνf(x)=x για κάθε x ανήκει R.
Θεωρούμε x1, x2 ανήκουν R με f(x1)=f(x2) οπότε προκύπτει 3f(x1)=3f(x2) και συνf(x1)=συνf(x2). Προσθέτοντας κατά μέλη προκύπτει:
3f(x1)+συνf(x1)=3f(x2)+συνf(x2) => x1=x2
Άρα η f είναι 1-1 και συνεπώς αντιστρέψιμη. Επομένως ισχύει η ισοδυναμία:
y=f(x) <=> x=(f-1)(y) όπου x ανήκει R και y ανήκει f(R)=R
Συνεπώς έχουμε (f-1)(y)=3y+συνy όπου y ανήκει R. Άρα (f-1)(x)=3x+συνx για κάθε x ανήκει R. Έχουμε:
(f-1)(x)=3x+συνx <=> [(f-1)(x)-συνx]/3=x για κάθε x ανήκει R
β) (f-1)(0)=3*0+συν0=0+1=1 <=> f(1)=0
(f-1)(π/2)=3*(π/2)+συν(π/2)=(3π/2) <=> f(3π/2)=π/2
Άρα η Cf διέρχεται από τα σημεία Α(1,0) και Β(3π/2,π/2)
γ) f(f(f(x)+1)+(3π/2))=π/2 <=> f(f(f(x)+1)+(3π/2))=f(3π/2) <=> f(f(x)+1)+(3π/2)=3π/2 <=> f(f(x)+1)=0 <=> f(f(x)+1)=f(1) <=> f(x)+1=1 <=> f(x)=0 <=> f(x)=f(1) <=> x=1
δ) Η συνάρτηση f-1 είναι συνεχής και παραγωγίσιμη στο R με πρώτη παράγωγο:
(f-1)΄(y)=3-ημy
Για y=0 έχουμε (f-1)(0)=1 και (f-1)΄(0)=3. Από τον ορισμό της παραγώγου συνάρτησης σε σημείο έχουμε:
lim(y->0){[(f-1)(y)-(f-1)(0)]/(y-0)}=(f-1)΄(0) <=> lim(y->0){[(f-1)(y)-1]/y}=3
Άρα lim(x->0){[(f-1)(x)-1]/x}=3 <=> lim(x->0){[((f-1)(x)-1)/x]-3}=0
Για κάθε y ανήκει R ισχύει -1<=συνy<=1 => 3y-1<=3y+συνy<=3y+1 => 3y-1<=(f-1)(y)<=3y+1
Για y>1/3 ισχύει 3y-1>0 και 37+1>2>0, οπότε έχουμε:
3y-1<=(f-1)(y)<=3y+1 => 1/(3y+1)<=1/(f-1)(y)<=1/(3y-1) => y/(3y+1)<=y/(f-1)(y)<=y/(3y-1)
Επειδή lim(y->+oo)[y/(3y-1)]=lim(y->+oo)[y/(3y+1)]=lim(y->+oo)[y/(3y)]=lim(y->+oo)(1/3)=1/3 τότε σύμφωνα με το κριτήριο παρεμβολής προκύπτει lim(y->+oo)[y/(f-1)(y)]=1/3
Επειδή lim(y->+oo)(3y-1)=lim(y->+oo)(3y+1)=lim(y->+oo)(3y)=+oo τότε σύμφωνα με το κριτήριο παρεμβολής προκύπτει
lim(y->+oo)(f-1)(y)=+oo
Θεωρούμε τον μετασχηματισμό y=f(x) <=> x=(f-1)(y). Επειδή lim(y->+oo)(f-1)(y)=+oo τότε έχουμε:
lim(x->+oo)[f(x)/x]=lim(y->+oo)[y/(f-1)(y)]=1/3
Συνεπώς lim(x->+oo)[f(x)/x]=1/3 <=> lim(x->+oo){[f(x)/x]-(1/3)}=0
ε) Όπως αναφέρθηκε η f-1 είναι συνεχής και παραγωγίσιμη στο R με πρώτη παράγωγο (f-1)΄(y)=3-ημy. Για κάθε y ανήκει R ισχύει -1<=ημy<=1, οπότε έχουμε:
-1<=ημy<=1 => -1<=-ημy<=1 => 2<=3-ημy<=4 => 2<=(f-1)΄(y)<=4 => (f-1)΄(y)>0 για κάθε y ανήκει R
Επειδή η f-1 είναι συνεχής και παραγωγίσιμη στο R και ισχύει (f-1)΄(y)>0 για κάθε y ανήκει R τότε η f-1 είναι γνησίως αύξουσα στο R.
Επειδή η f-1 είναι γνησίως αύξουσα στο R τότε και η f είναι γνησίως αύξουσα στο R.
Επειδή η f-1 είναι παραγωγίσιμη στο R και ισχύει (f-1)΄(y) διάφορο 0 για κάθε y ανήκει R τότε η f είναι πραγωγίσιμη στο R (δεν χρειάζεται να δώσει η εκφώνηση ότι η f είναι παραγωγίσιμη στο R αφού προκύπτει από τα δεδομένα) με πρώτη παράγωγο:
f΄(x)=1/(f-1)΄(f(x)), x ανήκει R
Για x=1 προκύπτει f΄(1)=1/(f-1)΄(f(1))=1/(f-1)΄(0)=1/3
Η εφαπτομένη της Cf στο σημείο Α(1,f(1)) έχει εξίσωση:
y-f(1)=f΄(1)(x-1) => y-0=(1/3)(x-1) => y=(1/3)x-(1/3)
Θεωρούμε την συνάρτηση
g(x)=(f-1)(x)-[(1/3)x-(1/3)]=3x+συνx-(1/3)x+(1/3)=(8/3)x+συνx+(1/3), x ανήκει R
Η g είναι συνεχής στο R
g(-π/2)=(1-4π)/3<0
g(0)=4/3>0
Η g είναι συνεχής στο [-π/2,0] και ισχύει g(-π/2)g(0)<0. Επομένως σύμφωνα με το θεώρημα Bolzano υπάρχει τουλάχιστον ένα x0 ανήκει (-π/2,0) τέτοιο ώστε g(x0)=0 <=> (f-1)(x0)=(1/3)x0-(1/3)=y0 όπου y0=(1/3)x0-(1/3)
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 3 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 227 μέλη διάβασαν αυτό το θέμα:
- hristosdab
- trifasikodiavasma
- haji
- thepigod762
- Mariosm.
- soulatso
- oteletampis
- phleidhs
- Hased Babis
- AggelikiGr
- sir ImPeCaBlE
- veiNqh
- Scandal
- alekos
- Debugging_Demon
- just some guy
- xristosgkm
- ismember
- Apocalypse
- arrow25
- rempelos42
- ggl
- GStef
- QWERTY23
- xrisamikol
- Σωτηρία
- nikoletaz57
- _Aggelos123
- Mariam38
- SlimShady
- strsismos88
- Georgekk
- Lia 2006
- igeorgeoikonomo
- marian
- tsiobieman
- constansn
- Xristosdimitra
- Panagiotis849
- ρενακι 13
- Memetchi
- eukleidhs1821
- Nikkkpat
- Unboxholics
- korlef
- kwstaseL
- Thanos_D
- the purge
- T C
- Giii
- Papachrist
- liaiscool
- Αννα Τσιτα
- globglogabgalab
- Pharmacist01
- thanahss
- abcdefg12345
- nicole1982
- thecrazycretan
- kvstas92
- KingOfPop
- maria301
- papa2g
- stefan
- Κλημεντίνη
- TonyMontanaEse
- Athens2002
- Alexecon1991
- Μάρκος Βασίλης
- Cortes
- το κοριτσι του μαη
- calliope
- ale
- panagiotis G
- Kleanth
- aggelosst9
- BioChemical
- spring day
- nucomer
- Georgia110
- LeoDel
- pink_panther
- Alexandros973
- marsenis
- den antexw allh apotyxia
- KaterinaL
- kiyoshi
- drosos
- Λαμπρινηη
- Bill22
- Chrysablac.
- giorgosp97
- Βλα
- Monster Hunter
- jul25
- xxxtolis
- Stroka
- nicks1999
- totiloz
- Earendil
- mitsakos
- tasost
- lnesb
- ssalex
- Vasilina93
- alan09
- Livaja10
- χημεια4λαιφ
- Viedo
- UncleJ
- Kostakis45
- Infrared
- Zgian
- pepatogourounaki
- hirasawayui
- GeoCommand
- Eleni54
- American Economist
- EiriniS20
- ΘανάσοςG4
- stamoul1s
- Αριάνα123
- uni77
- Libertus
- tasoss
- PanosCh002
- Unseen skygge
- Νικόλας Ραπ.
- cel123
- The Limit Does Not Exist
- don_vito
- suaimhneas
- Αλκης Κ.
- alexrami
- Baggelitsa36
- Νομικάριος13
- spinalgr1990
- d_th
- Adolfo valencia
- Πα.Κ
- Vasilis25
- Johnman97
- Steffie88
- rekcoR
- gwgw_5
- fockos
- Mariahj
- roud
- kostas83
- Cpt.Philips
- Makis45
- Χρησλου
- Panos_02
- Vold
- tymvorixos
- GiorgosAsi
- Neos167
- theodoraooo
- George187
- Άρτεμις Α.
- Μαρία2222
- christos87
- Idontknoww
- jimis2001
- Metamorph
- Γατόπαρδος.
- Johnsk
- mitsos14
- johnsiak
- Elel
- Dreamer_SW
- Γιαννης1987Θεσσ
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki




