

Μία προσπάθεια:
Δίνεται (ε):και έστω
κοινό σημείο της (ε) με την Cf.Άρα το Κ επαληθεύει την (ε):
Αφού Κ,Μ ανήκουν στην ίδια ευθεία όμοια ισχύει ότι
Άρα από rolle υπάρχει
ώστε f''(ξ)=0, άτοπο.

Λοιπόν, άκυρο. Δεν ξέρω αν το M επαληθεύει την εφαπτομένη στο Κ.
Δίνεται (ε):
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Guest 018946
Επισκέπτης


Έστω φ R->R 2 φορες παρμ/η με
φ(α)=κe^a
φ(c)=κe^c
φ(b)=κe^b
c \in (a,b)
Να δείξετε οτι υπάρχει ξ στο (α,β) τέτοιο ώστε 2φ'(ξ)=φ(ξ)+φ''(ξ)
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Guest 018946
Επισκέπτης


Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
C.J.S.
Νεοφερμένο μέλος
Civilara
Περιβόητο μέλος


Καλησπέρα.Έχω μια άσκηση και θέλω βοηθειά!!
Έχουμε: View attachment 55707 και μας ζητάει να βρούμε την F(x).
Πως την βρίσκω;;;
Πρέπει να διευκρινήσεις σε ποιο υποσύνολο του R ανήκουν τα x και y.
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
C.J.S.
Νεοφερμένο μέλος


χ,y>0 και
F'(1)=3
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


H σχέση γράφεταιΚαλησπέρα.Έχω μια άσκηση και θέλω βοηθειά!!
Έχουμε: View attachment 55707 και μας ζητάει να βρούμε την F(x).
Πως την βρίσκω;;;
Για
οπότε
δηλαδή
οπότε
και για
Καλή χρονιά σε όλους !!
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
C.J.S.
Νεοφερμένο μέλος


H σχέση γράφεται
.
Γιαστην (1) παίρνουμε
Για
με
είναι:
οπότε
δηλαδή
οπότε
=3 \ln x +\frac{x^2}{2}-x+c)
και για:
.
Καλή χρονιά σε όλους !!
Ευχαριστώ πολύ για την απάντηση!!Να σαι καλά βοηθάς πολύ εδώ μέσα!!
Καλή χρονιά με υγεία και ευτυχία!!
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Guest 018946
Επισκέπτης


Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
DumeNuke
Τιμώμενο Μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
DumeNuke
Τιμώμενο Μέλος


Περίμενα να μπορώ να το διορθώσω. Τέλος πάντων, το παραπάνω είναι λάθος (αντικαθιστώ την f'(x) με f'(ξ), διατηρώντας την f(x) ακέραιη.
Δεύτερη προσπάθεια, με εφαρμογή μονοτονίας.
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Civilara
Περιβόητο μέλος


Έστωμία παραγωγίσιμη συνάρτηση με
και
. Να δείξετε ότι
=0,\,\,\forall x \in \mathbb{R})
|f΄(x)|<=f(x) <=> -f(x)<=f΄(x)<=f(x) για κάθε x ανήκει R
Θεωρούμε τις συναρτήσεις g(x)=f(x)(e^x) και h(x)=f(x)(e^(-x)), x ανήκει R. Επειδή η f είναι παραγωγίσιμη στο R Τότε και οι g, h είναι παραγωγίσιμες στο R με πρώτη παράγωγο:
g΄(x)=(f΄(x)+f(x))(e^x)
h΄(x)=(f΄(x)-f(x))(e^(-x))
-f(x)<=f΄(x) => f΄(x)+f(x)>=0 => g΄(x)>=0, x ανήκει R
f΄(x)<=f(x) => f΄(x)-f(x)<=0 => h΄(x)<=0, x ανήκει R
Οι συναρτήσεις f, g, h είναι συνεχείς στο R ως παραγωγίσιμες στο R.
g(0)=f(0)=0
h(0)=f(0)=0
Η συνάρτηση g είναι συνεχής και παραγωγίσιμη στο R και ισχύει g΄(x)>=0 για κάθε x ανήκει R. Επομένως η g είναι αύξουσα στο R. Έχουμε:
x>0 => g(x)>=g(0) => f(x)(e^x)>=0 => f(x)>=0
x<0 => g(x)<=g(0) => f(x)(e^x)<=0 => f(x)<=0
Η συνάρτηση h είναι συνεχής και παραγωγίσιμη στο R και ισχύει h΄(x)<=0 για κάθε x ανήκει R. Επομένως η h είναι φθίνουσα στο R. Έχουμε:
x>0 => h(x)<=h(0) => f(x)(e^(-x))<=0 => f(x)<=0
x<0 => h(x)>=h(0) => f(x)(e^(-x))>=0 => f(x)>=0
Για x<0 ισχύουν f(x)<=0 και f(x)>=0. Άρα f(x)=0.
Για x>0 ισχύουν f(x)<=0 και f(x)>=0. Άρα f(x)=0.
Επειδή για x διάφορο 0 ισχύει f(x)=0 και f(0)=0 τότε f(x)=0 για κάθε x ανήκει R.
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


 .Ας επαναφέρουμε κι αυτές τις δύο που ξεχάστηκαν.
.Ας επαναφέρουμε κι αυτές τις δύο που ξεχάστηκαν. Έστωσυνεχής στο
, παραγωγίσιμη στο
, με
και
. Δείξτε ότι υπάρχουν
με
+\ell f'(\xi_2)+mf'(\xi_3)=0)
Για την πολυωνυμική και μη σταθερή συνάρτησηισχύει
για κάθε
α) Να αποδείξετε ότι
β) Να βρεθεί η εξίσωση της εφαπτομένηςτης
που σχηματίζει οξεία γωνία με τον άξονα
και διέρχεται από το σημείο
γ) Να βρείτε την ελάχιστη τιμή της παράστασης
Πηγή
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
DumeNuke
Τιμώμενο Μέλος


Έστωσυνεχής στο
, παραγωγίσιμη στο
, με
και
. Δείξτε ότι υπάρχουν
με
+\ell f'(\xi_2)+mf'(\xi_3)=0)
3 φορές ΘΜΤ στα υποδιαστήματα του (α,β).
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Eliminated
Εκκολαπτόμενο μέλος


Δίνεται συνάρτησηδύο φορές παραγωγίσιμη για την οποία ισχύει
, για κάθε
. Να δείξετε ότι η εφαπτομένη της
στο σημείο
δεν έχει άλλο κοινό σημείο με την
εκτός του
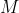
ή απλά αφού η f είναι κυρτή, κάθε εφαπτομένη βρίσκεται "κάτω" από τη Cf, εκτός από το σημείο επαφής.
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Mariaal
Εκκολαπτόμενο μέλος


1. Δίνονται οι μιγαδικοι αριθμοι z= 1+iα^χ (το α είναι υψωμένο εις τη χ) , w=x+1+i και η συνάρτηση f(x)= x|z|^2 + |w-1|^2 με χ ανήκει R και α > 0. Αν ισχύει | z - w:συζηγής| <= | z:συζυγής + w|
Α) να δείξετε ότι α= e
B) να βρείτε τα limf(x) οταν το χ τείνει στο +άπειρο και στο -άπειρο
Γ) να δείξετε ότι η Cf δεν έχει ασύμπτωτες
Δ) να δείξετε ότι η εξίσωση f(x)=0 είναι αδύνατη στο R.
2. Δίνεται η g(x)= (e^x - 1)/ (e^x + 1) με x ανήκει στο R. Θεωρούμε επίσης την παραγωγίσιμη συνάρτηση f(0,+άπειρο)->R για την οποία ισχύουν:
• f(e) = limg(x) το χ τείνει στο +άπειρο
• χf'(x)=1, για κάθε χ>0
Α) να βρείτε τον τύπο της f
Β) να βρείτε το όριο lim(f(x)+f'(x)) το χ τείνει στο 0+
Γ) να μελετήσετε την g ως προς τη μονοτονία, κυρτότητα, σημεία καμπής
Ε) να λύσετε την εξίσωση (e^συνχ•e^(2x) - 1)(e+1)=(e^συνχ•e^(2x) +1)(e-1)
3. Δίνεται f:R ->R 2 φορές παταγωγίσιμη για την οποία ισχύει:
Lim[(xf(x)-ημχ)/(e^(x^2)-1)]=1 το χ τείνει στο 0. Θεωρούμε g
 0,+άπειρο)->R με g(x)=x^2+x-2-f(2)lnx η γραφική παράσταση της οποίας δεν έχει κανένα τμήμα της κάτω απο τον xx'.
0,+άπειρο)->R με g(x)=x^2+x-2-f(2)lnx η γραφική παράσταση της οποίας δεν έχει κανένα τμήμα της κάτω απο τον xx'.A) να δείξετε ότι f(2)=3
Β) να μελετήσετε την g ως προς τη μονοτονία
Γ) να βρεθούν τα limg(x) όταν χ τείνει στο 0+ και στο +άπειρο
Δ) να βρεθεί η εξίσωση της εφαπτομένης της Cf στο σημείο που τέμνει τον yy'
E)να αποδείξετε ότι υπάρχει χ0 ανήκει (0,2) τέτοιο ώστε f"(x0)=0
Στ) να αποδείξετε ότι η f(x)-2x=(1-x)f'(x) έχει μία τουλάχιστον ρίζα στο (0,2)
Ζ) αν επιπλέον ισχύει ότι f'(x)
 για κάθε χ να αποδείξετε ότι υπάρχει ένα τουλάχιστον ξ ανήκει (-2,4) τέτοιο ώστε 3f(ξ)=7ξ-1.
για κάθε χ να αποδείξετε ότι υπάρχει ένα τουλάχιστον ξ ανήκει (-2,4) τέτοιο ώστε 3f(ξ)=7ξ-1.Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Guest 018946
Επισκέπτης


παίζει τίποτα σε υποδειξη για το τελευταιο; γιατι σκεφτηκα την 2(x^2+y^2) \geq (x+y)^2 αλλα δεν μπορω να την προχωρήσωΣωστά!.Ας επαναφέρουμε κι αυτές τις δύο που ξεχάστηκαν.
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
rebel
Πολύ δραστήριο μέλος


Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
nikoslarissa
Δραστήριο μέλος


Να βρείτε τον τύπο της αν
Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.
Χρήστες Βρείτε παρόμοια
-
Τα παρακάτω 0 μέλη και 5 επισκέπτες διαβάζουν μαζί με εσάς αυτό το θέμα:Tα παρακάτω 288 μέλη διάβασαν αυτό το θέμα:
- trifasikodiavasma
- ggl
- ioanna2007
- Hased Babis
- thepigod762
- akis_95
- Mariosm.
- Maynard
- infection54
- Jesse_
- topg
- eukleidhs1821
- bill09876
- Debugging_Demon
- mali
- Joji
- Ness
- Helen06
- Scandal
- synthnightingale
- arko
- BillyTheKid
- Magigi
- Paragontas7000
- Unboxholics
- just some guy
- george777
- Wonderkid
- IceCream05
- Abiogenesis
- GeorgePap2003
- katia.m
- giannhs2001
- paul
- Praxis
- Apocalypse
- shezza94
- desp1naa
- rempelos42
- Sherlockina
- oups
- Dimgeb
- spring day
- KingOfPop
- mpapa
- Chrisa
- Physicsstudent
- tsiobieman
- P.Dam.
- persi
- theodoraooo
- PanosBat
- kost28
- mikriarchitectonissa
- BILL KEXA
- Dr. Gl. Luminous
- Eleftheria2
- Athens2002
- bruh_234
- Miranda32
- SlimShady
- kallikd
- nucomer
- alpha.kappa
- Eeeee
- J.Cameron
- Marple
- Kitana
- F1L1PAS
- sophiaa
- VFD59
- papa2g
- το κοριτσι του μαη
- srg96
- Hopeful22
- Φινεύς
- Phys39
- Anta2004
- fairyelly
- Pharmacist01
- jYanniss
- Panagiotis849
- Kokro
- augustine
- Nikoletaant
- Mashiro@Iberan
- margik
- Mammy Nun
- Pastramis
- Σωτηρία
- Appolon
- panosveki
- Nickt23
- igeorgeoikonomo
- Steliosgkougkou
- QWERTY23
- Ameliak
- aladdin
- nimbus
- Φωτεινη Τζα.
- marian
- Georgekk
- xrisamikol
- the purge
- Theodora03
- Machris
- s93060
- Nikitas18
- Stif6
- stav.mdp
- damn
- aekaras 21
- Anthropaki
- Angelos12345
- ioannam
- Μάρκος Βασίλης
- skyway
- Nick2325
- Nala
- Manolo165
- Ryuzaki
- T C
- Devilshjoker
- El_
- George9989
- TonyMontanaEse
- globglogabgalab
- constansn
- barkos
- katerinavld
- fenia
- An_uknown_world
- Jimmis18
- maria2001
- KingPoul
- Xara
- thecrazycretan
- abcdefg12345
- Κλημεντίνη
- ale
- panagiotis G
- mechaniceng
- Giii
- calliope
- Tequila
- natalix
- Cortes
- Alexecon1991
- pepsoula
- Mariaathens
- Lia 2006
- 1205
- παιδι για κλαματα
- Alexandros36k
- alexd99
- chembam
- Specon
- Dr House
- panagiotis23
- Johnman97
- rhymeasylum
- Αννα Τσιτα
- KaterinaL
- Libertus
- LeoDel
- iminspain
- den antexw allh apotyxia
- Λαμπρινηη
- Mendel2003
- Ijt
- drosos
- Κορώνα
- JohnGreek
- Αρχηγος_β3
- alexandra_
- ΘανάσοςG4
- Dimitris9
- Birtjan
- george7cr7
- NickT
- Bgpanos
- JKTHEMAN
- nicole1982
- χημεια4λαιφ
- Stroka
- Kostakis45
- charmander
- leo41
- EiriniS20
- Αριάνα123
- MarilynSt
- iManosX13
- Nefh_
- Viedo
- Βλα
- suaimhneas
- george pol
- kristinbacktoschool
- fearless
- Rene2004
- Steffie88
- Slytherin
- jimnikol21
- Unseen skygge
- cel123
- jul25
- Thanos_D
- Ireneeneri
- tasost
- Mukumbura
- xxxtolis
-
Φορτώνει...
-
Το forum μας χρησιμοποιεί cookies για να βελτιστοποιήσει την εμπειρία σας.
Συνεχίζοντας την περιήγησή σας, συναινείτε στη χρήση cookies στον περιηγητή σας.
 Αρχική Forum
Αρχική Forum
 Ρωτήστε κάτι
Ρωτήστε κάτι
 Προσωπικές Συζητήσεις
Προσωπικές Συζητήσεις
 Πανελλαδικές
Πανελλαδικές
 Αγγελίες
Αγγελίες
 Συνδεδεμένοι Χρήστες
Συνδεδεμένοι Χρήστες
 Λίστα Αποκλεισμένων
Λίστα Αποκλεισμένων
 Υπεύθυνοι του Forum
Υπεύθυνοι του Forum
 e-steki
e-steki

