Συλλογή ασκήσεων και τεστ στα Μαθηματικά Προσανατολισμού

iDexter · 29-11-13

Γεια σε όλους,
Φέτος δίνω πανελλήνιες και εγώ και έχω ενα θέμα.Ανέκαθεν θεωρούσα δυσκολότερο μάθημα (συγκριτικά) τη φυσική,αφήνοντας τα μαθηματικά σε 2η μοίρα αφου εύκολα ή δύσκολα έλυνα κάθε άσκηση...Η αντιμετώπιση αυτή όμως με οδήγησε στο εξης φαινόμενο:
Λύνω την πιο άκυρη άσκηση στη φυσική εύκολα και στα μαθηματικά κολλάω...Σαν να έχω χάσει την φαντασία που χρειάζεται ή την οξυδέρκεια μου ή κατι τέτοιο,την οποία είχα σε αρκετά μεγάλο βαθμό...Έτσι έβγαλα το συμπέρασμα ότι πρέπει να αρχίσω τα μαθς με σοβαρό τρόπο..Γιιιιιιιιιιιιιιιι'αυτό λοιπόν θέλω να μου στείλετε ασκήσεις (Μέχρι πορίσματα ΘΜΤ) οι οποίες να στέκονται στο ύψος των πανελληνίων ή ακόμα και δυσκολότερες γιατί νοιώθω ότι στο φροντιστήριο είναι σχετικά απλά τα πράγματα :hmm:

Εν ολίγοις θέλω θέματα που θα με βοηθήσουν να τελειοποιήσω τις τεχνικές και το "μάτι" μου έτσι ώστε να γράψω το πολυπόθητο 100άρι στο τέλος(έχω και ένα στοίχημα να κερδίσω ^^ ) ,
Ευχαριστώ εκ των προτέρων

DimX · 29-11-13

δες τα θεματα της μαθηματικης εταιριας!believe me αξιζουν!

Guest 018946 · 01-12-13

Παιζει τιποτα σε ντοπε ;

rebel · 01-12-13

1) Η συνάρτηση $f: \mathbb{R} \to \mathbb{R}$ είναι συνεχής και είναι:
$f(1)+f(2)+\cdots + f(\nu)=\frac{\nu (\nu+1)}{2}.$
Να δειχθεί ότι υπάρχει $x_0 \in [1,\nu]$ τέτοιο ώστε $f\left(x_0\right)=x_0$
2) Αν για την συνάρτηση $f:\left(0,+\infty \right) \to \mathbb{R}$ ισχύει $f(x)-f(y) \geq \ln \frac{x}{y}+x-y$ για κάθε $x,y \in \left(0,+\infty \right)$ και $f(1)=1$ , να βρείτε τον τύπο της $f$

Guest 018946 · 1 Δεκεμβρίου 2013

για την πρώτη

ορίζω την

$g(x)=f(x)-x , x \in [1,n]$

παρατηρω ότι $g(1)+...+g(n)=0$

εστω οτι δεν είχε καμία ρίζα στο [1,ν] τότε θα ηταν παντού θετικη αρνητικη αφου ειναι συνεχης κατι το οποίο ειναι ατοπο άρα θα υπάρχει τουλάχιστον μία ρίζα στο [1,ν]

για την αλλη μπορω να πώ οτι για ψ=1

φ(χ) >= lnx+x

x=1 , => φ(y) <= lny+y

και τώρα ειναι προφανές ότι φ(χ)=lnx+x , x >0

rebel · 01-12-13

Δεν ήταν και τόσο ντοπέ τελικά

. Άλλη μία:
Έστω $f:[a,b] \to \mathbb{R}$ συνεχής συνάρτηση. Υποθέτουμε ότι για κάθε $x \in [a,b]$ υπάρχει $y \in [a,b]$ ώστε $\left|f(y)\right| \leq \frac{1}{2}\left|f(x)\right|$ . Να αποδειχθεί ότι υπάρχει $\xi \in [a,b]$ ώστε $f(\xi)=0$

Guest 018946 · 01-12-13

έστω οτι δεν υπήρχε λογω συνεχειας φ(χ)>0 ή φ(χ) < 0

για φ(χ)>0

φ(ψ)<φ(χ)/2

για αφου ισχύει για καθε χ στο [α,β] θα ισχυει και για χ=ψ
αρα θετοντας στην ανισοτητα

-φ(ψ)/2>0 => φ(ψ)<0 ατοπο αφου έχουμε υποθέσει οτι η συναρτηση μας ειναι θετικη στο [α,β]
αρα υπαρχει καποιος ξ στο [α,β] τετοιος ωστε φ(ξ)=0

ομοια καταληγω σε ατοπο αν θεωρησω οτι φ(χ)<0

rebel · 1 Δεκεμβρίου 2013

Αρχική Δημοσίευση από dr.tasos:
για αφου ισχύει για καθε χ στο [α,β] θα ισχυει και για χ=ψ

Για το συγκεκριμένο $y$ όμως υπάρχει $y_1$ τέτοιο ώστε $f(y_1) \leq f(y)/2$ χωρίς να είναι κατ' ανάγκη $y=y_1$ . O τρόπος πάντως είναι σωστός: Αν δεν υπήρχε τέτοιο $\xi \in [a,b]$ , η $f$ θα διατηρούσε πρόσημο κλπ. Για να καταλήξεις σε άτοπο μπορείς να εκμεταλλευτείς μία άλλη ιδιότητα των συνεχών συναρτήσεων σε κλειστά διαστήματα: την μέγιστη και ελάχιστη τιμή (ίσως πρόδωσα την λύση).

Guest 018946 · 01-12-13

πωωωω την πατησα σαν αγραμματος ...

αμα ειναι θετικη φ(ψ)=<φ(χ)/2

θα εχει ελαχιστο αρα θα υπαρχει χ1 τετοιο ωστε φ(χ)>=φ(χ1) (1) μα η σχεση με την ανισοτητα δινει τουλαχιστον ενα κ τετοιο ωστε φ(κ)*2=<φ(χ1)

η (1) για χ=κ δινει φ(κ)>=φ(χ1) και τωρα αφου η φ ειναι θετικη ειναι προφανες οτι εχουμε αντιφαση

rebel · 01-12-13

Σωστά. Ανάλογα αν ήταν $f(x)<0,\,\,\forall x \in [a,b]$ τότε για κάθε $x \in [a,b]$ θα υπήρχε $y \in [a,b]$ τέτοιο ώστε $-f(y) \leq -f(x)/2 \Rightarrow f(y) \geq f(x)/2$ οπότε αν παρουσιάζει μέγιστο για $x=x_1 \in [a,b]$ , υπάρχει $y_1 \in [a,b]$ τέτοιο ώστε $f(y_1) \geq f(x_1)/2 \Rightarrow 2f(y_1) \geq f(x_1)$ και λόγω μεγίστου ισχύει $f(x_1) \geq f(y_1)$ οπότε $f(y_1) \geq 0$ , άτοπο και πάλι.

rebel · 02-12-13

Σε μία δεξαμενή που έχει σχήμα κώνου χύνεται νερό με ρυθμό $5\pi \,\, m^3/sec$ . To ύψος του κώνου είναι $h=20m$ και η ακτίνα της βάσης είναι $r=10m$ . Να βρείτε πόσο γρήγορα ανεβαίνει η στάθμη του νερού στη δεξαμενή κατά την χρονική στιγμή που το ύψος της στάθμης είναι $5m$ .

(Δίνεται ο τύπος $V=\frac{\pi r^2 h}{3}$ για τον όγκο του κώνου)

Guest 018946 · 08-12-13

Δεν βλέπω τιποτα !

rebel · 08-12-13

Από το παραπάνω σχήμα ο όγκος του νερού στον χρόνο $t$ σύμφωνα με τον τύπο είναι:
$V(t)=\frac{\pi x^2(t) y(t)}{3}$
Τώρα, όπως σε παρεμφερή προβλήματα με εμβαδά, όγκους κλπ πρέπει να βρεις μία σχέση μεταξύ των διαστάσεων $x(t),y(t)$ για να προχωρήσεις.

Civilara · 08-12-13

Αρχική Δημοσίευση από styt_geia:
Σε μία δεξαμενή που έχει σχήμα κώνου χύνεται νερό με ρυθμό $5\pi \,\, m^3/sec$ . To ύψος του κώνου είναι $h=20m$ και η ακτίνα της βάσης είναι $r=10m$ . Να βρείτε πόσο γρήγορα ανεβαίνει η στάθμη του νερού στη δεξαμενή κατά την χρονική στιγμή που το ύψος της στάθμης είναι $5m$ .

(Δίνεται ο τύπος $V=\frac{\pi r^2 h}{3}$ για τον όγκο του κώνου)

Σε ύψος y(t) από την κορυφή του κώνου, ο κύκλος που προκύπτει από την τομή του κώνου με επίπεδο κάθετο στον άξονα του, έχει ακτίνα x(t) όπως στο σχήμα. Είναι 0<=x(t)<=r για 0<=y(t)<=h. Θεωρούμε τα ορθογώνια τρίγωνα, που προκύπτουν από ένα οποιοδήποτε επίπεδο στο οποίο ανήκει ο άξονας του κώνου, με πλευρές y(t), x(t) και h, r αντίστοιχα των οποίων οι υποτείνουσες κείνται επί της γενέτειρας του κώνου ως ίχνος της τομής του επιπέδου με τον κώνο. Τα τρίγωνα αυτά είναι όμοια γιατί έχουν ίσες γωνίες. Από την ομοιότητα των τριγώνων προκύπτει:

x(t)/r=y(t)/h => x(t)=(r/h)y(t)

Για τον όγκο της κωνικής στήλης ύδατος έχουμε:

V(t)=(π/3)[x(t)^2]y(t) => V(t)=(π/3){[(r/h)y(t)]^2}y(t) => V(t)=[(π(r^2))/(3(h^2))][y(t)^3] (1) => y(t)=[(3V(t)(h^2))/(π(r^2))]^(1/3) (2)

Η παροχή του νερού Q=5π m^3/s ισούται με το ρυθμό μεταβολής V΄(t). Στην εκφώνηση αφήνεται να εννοηθεί ότι η παροχή είναι σταθερή σε κάθε χρονική στιγμή. Σε αυτήν την περίπτωση ισχύει V΄(t)=Q => V=Qt+V0 όπου V0 είναι ο όγκος του νερού την χρονική στιγμή t=0 που ξεκίνησε να προστίθεται νερό στον κύλινδρο. Προφανώς ισχύει 0<=V0<Vmax όπου Vmax=(π/3)(r^2)h.

Θα υποθέσουμε ότι η παροχή δεν είναι σταθερή και ότι την χρονική στιγμή t1>0 είναι Q(t1)=5π m^3/s. Συνεπώς την χρονική στιγμή t1 η συνάρτηση V είναι παραγωγίσιμη με πρώτη παράγωγο V΄(t1)=Q(t1)=5π m^3/s.

Επειδή η V είναι παραγωγίσιμη στο t1 τότε από την (2) προκύπτει ότι και η y είναι παραγωγίσιμη στο t1. Εφόσον η y είναι παραγωγίσιμη στο t1 τότε από την (1) για t=t1 προκύπτει:

V΄(t)=[(π(r^2))/(h^2)][y(t)^2]y΄(t)

Άρα V΄(t1)=[(π(r^2))/(h^2)][y(t1)^2]y΄(t1) => y΄(t1)=[V΄(t1)(h^2)]/[π(r^2)(y(t)^2)]

όπου y(t1)=5 m και V΄(t1)=5π m^3/s.

Επομένως

y΄(t1)=[5*π*(20^2)]/[π*(10^2)*(5^2)] => y΄(t1)=4/5 m/s=0,8 m/s

rebel · 09-12-13

Σωστά. Η άσκηση είναι από ένα παλιό βοήθημα του Γκατζούλη.

Guest 018946 · 12-12-13

παιζει ντοπα σε ροολε και θμτ;

panabarbes · 12-12-13

Δίνεται συνάρτηση $f:R\rightarrow R$ δύο φορές παραγωγίσιμη για την οποία ισχύει $f''\left(x \right) \succ 0$ , για κάθε $x\epsilon R$ . Να δείξετε ότι η εφαπτομένη της ${C}_{f}$ στο σημείο $M\left({x}_{1},f\left({x}_{1} \right) \right)$ δεν έχει άλλο κοινό σημείο με την ${C}_{f}$ εκτός του $M$

photon · 12-12-13

Αρχική Δημοσίευση από panabarbes:
Δίνεται συνάρτηση $f:R\rightarrow R$ δύο φορές παραγωγίσιμη για την οποία ισχύει $f''\left(x \right) \succ 0$ , για κάθε $x\epsilon R$ . Να δείξετε ότι η εφαπτομένη της ${C}_{f}$ στο σημείο $M\left({x}_{1},f\left({x}_{1} \right) \right)$ δεν έχει άλλο κοινό σημείο με την ${C}_{f}$ εκτός του $M$

Μία προσπάθεια:
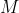
Δίνεται (ε): $y-f(x1)=f'(x1)(x-x1)$ και έστω $K(x2,f(x2))$ κοινό σημείο της (ε) με την Cf.Άρα το Κ επαληθεύει την (ε): $f(x2)-f(x1)=f'(x1)(x2-x1)\Rightarrow f'(x1)=\frac{f(x2)-f(x1)}{x2-x1}$ Αφού Κ,Μ ανήκουν στην ίδια ευθεία όμοια ισχύει ότι $f(x1)-f(x2)=f'(x2)(x1-x2)\Rightarrow f'(x2)=\frac{f(x1)-f(x2)}{x1-x2}=\frac{f(x2)-f(x1)}{x2-x1},f'(x1)=f'(x2)$ Άρα από rolle υπάρχει $\xi \in(x1,x2)$ ώστε f''(ξ)=0, άτοπο.

Guest 018946 · 12-12-13

ή και με ατοπο στην h(x)=f(x)-f'(x1)(x-x1) και μετα Rolle μπαινω σε άτοπο

Civilara · 12-12-13

Αρχική Δημοσίευση από panabarbes:
Δίνεται συνάρτηση $f:R\rightarrow R$ δύο φορές παραγωγίσιμη για την οποία ισχύει $f''\left(x \right) \succ 0$ , για κάθε $x\epsilon R$ . Να δείξετε ότι η εφαπτομένη της ${C}_{f}$ στο σημείο $M\left({x}_{1},f\left({x}_{1} \right) \right)$ δεν έχει άλλο κοινό σημείο με την ${C}_{f}$ εκτός του $M$

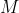
Η εφαπτομένη της Cf στο σημείο (x1,f(x1)) έχει εξίσωση:
y-f(x1)=f΄(x1)(x-x1) <=> y=f΄(x1)x+f(x1)-x1f(x1) <=> y=g(x) όπου g(x)=f΄(x1)x+f(x1)-x1f(x1), x ανήκει R

Θεωρούμε την συνάρτηση h με τύπο h(x)=f(x)-g(x) <=> h(x)=f(x)-f΄(x1)x-f(x1)+x1f(x1), x ανήκει R.
Παρατηρούμε ότι h(x1)=0 <=> f(x1)=g(x1)

Επειδή η f είναι δύο φορές παραγωγίσιμη στο R τότε και η h είναι δύο φορές παραγωγίσιμη στο R με πρώτη και δεύτερη παράγωγο:
h΄(x)=f΄(x)-f΄(x1)
h΄΄(x)=f΄΄(x)

Παρατηρούμε ότι h΄(x1)=0

Επειδή f΄΄(x)>0 για κάθε x ανήκει R τότε h΄΄(x)>0 για κάθε x ανήκει R. Επειδή η h είναι παραγωγίσιμη στο R τότε είναι και συνεχής στο R. Η h είναι συνεχής και δύο φορές παραγωγίσιμη στο R με h΄΄(x)>0 για κάθε x ανήκει R. Επομένως η h είναι κυρτή στο R που σημαίνει ότι η πρώτη παράγωγος h΄ είναι γνησίως αύξουσα στο R. Άρα

x<x1 => h΄(x)<h΄(x1) => h΄(x)<0 για κάθε x ανήκει (-oo,x1)
x>x1 => h΄(x)>h΄(x1) => h΄(x)>0 για κάθε x ανήκει (x1,+oo)

Η h είναι συνεχής στο (-οο,x1], παραγωγίσιμη στο (-οο,x1) και ισχύει h΄(x)<0 για κάθε x ανήκει (-οο,x1). Επομένως η h είναι γνησίως φθίνουσα στο (-οο,x1).
Η h είναι συνεχής στο [x1,+oo), παραγωγίσιμη στο (x1,+oo) και ισχύει h΄(x)>0 για κάθε x ανήκει (x1,+oo). Επομένως η h είναι γνησίως αύξουσα στο (x1,+oo).

x<x1 => h(x)>h(x1) => h(x)>0 για κάθε x ανήκει (-oo,x1)
x>x1 => h(x)>h(x1) => h(x)>0 για κάθε x ανήκει (x1,+oo)

Άρα ισχύει h(x)>0 για κάθε x ανήκει (-oo,x1)U(x1,+oo) και h(x1)=0. Συνεπώς η h παρουσιάζει ολικό ελάχιστο στο x1 και για κάθε x ανήκει (-οο,x1)U(x1,+oo) ισχύει h(x)>0 => h(x) διάφορο 0 που σημαίνει ότι η εφαπτομένη της Cf στο (x1,f(x1)) δεν έχει άλλο κοινό σημείο με την Cf.

Συλλογή ασκήσεων και τεστ στα Μαθηματικά Προσανατολισμού

Νεοφερμένος

Εκκολαπτόμενο μέλος

Guest 018946

Επισκέπτης

Πολύ δραστήριο μέλος

Guest 018946

Επισκέπτης

Πολύ δραστήριο μέλος

Guest 018946

Επισκέπτης

Πολύ δραστήριο μέλος

Guest 018946

Επισκέπτης

Πολύ δραστήριο μέλος

Πολύ δραστήριο μέλος

Guest 018946

Επισκέπτης

Πολύ δραστήριο μέλος

Περιβόητο μέλος

Πολύ δραστήριο μέλος

Guest 018946

Επισκέπτης

Εκκολαπτόμενο μέλος

Νεοφερμένος

Guest 018946

Επισκέπτης

Περιβόητο μέλος