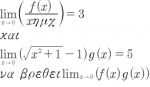Βοήθεια/Aπορίες στα Μαθηματικά Προσανατολισμού

[Artech]

Τα λυσάρια βλέπω πάνε και έρχονται.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[nPb]

Tι θες να πεις;

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Artech]

Ότι είσαι μεγάλος μαθηματικός...

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Μαριλινάκι]

Ευχαριστώ πολυ και εσένα nPb! με τη βοήθεια και των δυο σας πιστεύω ότι θα καταφέρω να λύσω και άλλες παρόμοιες ασκήσεις ! Ευχαριστώ!

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Chris1993]

Tι θες να πεις;

Θέλει να πεί ότι η λύση που έδωσες είναι καρμπόν από λυσάρια! (δηλαδή ότι το μόνο που έκανες είναι να την αντιγράψεις)
Αλλά μην απαντήσεις στις μικροπρέπειες του Artech.
Επιβεβαιώνει με τον καιρό (όλο και περισσότερο) πόσο λίγος και ανασφαλής είναι.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[nPb]

Θέλει να πεί ότι η λύση που έδωσες είναι καρμπόν από λυσάρια! (δηλαδή ότι το μόνο που έκανες είναι να την αντιγράψεις)
Αλλά μην απαντήσεις στις μικροπρέπειες του Artech.
Επιβεβαιώνει με τον καιρό (όλο και περισσότερο) πόσο λίγος και ανασφαλής είναι.

Ναι κατάλαβα τι είπε. Δεν θα απαντήσω και γενικά τον αποφεύγω γιατί τρολλάρει.

Ο λόγος που κάθησα και την ξανα-έλυσα καρμπόν είναι να τη βοηθήσω την κοπέλα, να μπει λίγο στη σκέψη βήμα-βήμα με τα λόγια που πρέπει να γράφονται. Την ενημέρωσα ότι πρόκειται για μια Συνήθη Διαφορική Εξίσωση οπότε και έχει βάση η αναφορά στην οικογένεια λύσεων, στην αρχική συνθήκη και στην ειδική (ιδιάζουσα) λύση. Όμως για τα πλαίσια του λυκείου, ας περιοριστούμε στο "τέχνασμα". Δεν έχω λυσάρι μαθηματικών λυκείου. Τα μαθηματικά λυκείου έχω να τα δω από τα 18 μου.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[aris-bas]

καλησπερα!!Οποιος μπορει ας βοηθησει στα παρακατω......σε καποια γραφω και τη λυση που σκεφτηκα..
1)


2)
εδω σκεφτηκα να διαιρεσω αριθμητη και παρονομαστη με χ

3)


4)


5)

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Civilara]

καλησπερα!!Οποιος μπορει ας βοηθησει στα παρακατω......σε καποια γραφω και τη λυση που σκεφτηκα..
1)

Για κάθε x ανήκει (-π/2,0)U(0,π/2) ισχύει 0<συνx<1 => συνx<1 => συνx-1<0

lim(x->0)(συνx-1)=συν0-1=1-1=0 και επειδή συνx-1<0 κοντά στο 0 τότε lim(x->0)[1/(συνx-1)]=-oo
lim(x->0)(3x-7)=3*0-7=-7<0

Επειδή lim(x->0)(3x-7)=-7<0 και lim(x->0)[1/(συνx-1)]=-oo τότε lim(x->0)[(3x-7)/(συνx-1)]=+oo

2)
εδω σκεφτηκα να διαιρεσω αριθμητη και παρονομαστη με χ

Για κάθε x ανήκει R ισχύει -1<=ημx<=1. Επομένως για κάθε x>0 ισχύει -1/x<=ημx/x<=1/x
Έχουμε lim(x->+oo)(1/x)=0 και lim(x->+oo)(-1/x)=-lim(x->+oo)(1/x)=-0=0
Επειδή lim(x->+oo)(-1/x)=-lim(x->+oo)(1/x)=0 τότε σύμφωνα με το κριτήριο παρεμβολής είναι lim(x-+oo)(ημx/x)=0

Επομένως lim(x->+oo)[2(ημx/x)-1]=2*0-1=-1

Θέτουμε u=2/x όπου x>0
lim(x->+oo)(2/x)=2*0=0
lim(x->+oo)[ημ(2/x)]=lim(x->0+)ημu=ημ0=0
lim(x->+oo)(3x)=+oo

Επειδή lim(x->+oo)(3x)=+oo και lim(x->+oo)[ημ(2/x)]=0 τότε lim(x->+oo)[3x+ημ(2/x)]=+οο. Άρα lim(x->+oo)[1/(3x+ημ(2/x))]=0

Έχουμε
lim(x->+oo)[(2ημx-x)/(3(x^2)+xημ(2/x))]=lim(x->+oo)[(2(ημx/x)-1)/(3x+ημ(2/x))]=
=lim(x->+oo)[2(ημx/x)-1]*lim(x->+oo)[1/(3x+ημ(2/x))]=(-1)*0=0

Άρα lim(x->+oo)[(2ημx-x)/(3(x^2)+xημ(2/x))]=0

3)

lim(x->+oo)[((4^x)+(5^x))/(3^x)]=lim(x->+oo){[(4^x)/(3^x)]+[(5^x)/(3^x)]}=lim(x->+oo)[((4/3)^x)+((5/3)^x)]=+oo
επειδή lim(x->+oo)((4/3)^x)=lim(x->+oo)((5/3)^x)=+oo και αυτό επειδή 4/3>1 και 5/3>1

4)

lim(x->+oo)[((3^x)+(4^x))/(5^x)]=lim(x->+oo){[(3^x)/(5^x)]+[(4^x)/(5^x)]}=lim(x->+oo)[((3/5)^x)+((4/5)^x)]=
=lim(x->+oo)[((3/5)^x)]+lim(x->+oo)[((4/5)^x)]=0+0=0 και αυτό επειδή 3/4<1 και 3/5<1

5)

Θέτουμε u=e^x
lim(x->+oo)(e^x)=+oo

lim(x->+oo){[(e^x)+(e^(-x))]/[(e^x)-(e^(-x))]}=lim(x->+oo){[((e^x)^2)+1]/[((e^x)^2)-1]}=lim(u->+oo){[(u^2)+1]/[(u^2)-1]}=
=lim(u->+oo)[(u^2)/(u^2)]=lim(u->+oo)1=1

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[hliass_1989]

f(x)=e^-x .Απο ποιο σημειο της f πρεπει να φερω παραλληλες ως προς τους αξονες, ωστε το ορθογωνιο που θα σχηματιστει να εχει μεγιστο εμβαδον?

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Civilara]

f(x)=e^-x .Απο ποιο σημειο της f πρεπει να φερω παραλληλες ως προς τους αξονες, ωστε το ορθογωνιο που θα σχηματιστει να εχει μεγιστο εμβαδον?

Αν M(x,f(x)) ένα σημείο της Cf τότε εννοείς το ορθογώνιο παραλληλόγραμμο με κορυφές τα σημεία Ο(0,0), Α(x,0), B(0,f(x)) και M(x,f(x));

Σε αυτήν την περίπτωση το εμβαδόν του ορθογωνίου τείνει στο +οο όταν x->-oo. Δεν υπάρχει μέγιστη τιμή.

Μάλλον δεν έχεις γράψει σωστά την εκφώνηση. Ας κάνω όμως την ανάλυση μου.

Το ορθογώνιο με κορυφές τα σημεία Ο, Α, Β και Μ που αναφέρθηκαν παραπάνω έχει εμβαδό:
Ε(Ω)=(ΟΑ)*(ΟΒ)=|x|*|f(x)|=|x|*|e^(-x)|=|x|*(e^(-x))=g(x) όπου x ανήκει R

Για x=0 το ορθογώνιο εκφυλίζεται σε μία γραμμή και ορθώς προκύπτει g(0)=0

Αν x<0 τότε |x|=-x, οπότε g(x)=-x(e^(-x)), x<0
Αν x>=0 τότε |x|=x, οπότε g(x)=x(e^(-x)), x>=0

Για x<0 είναι g(x)=-x(e^(-x)). Επομένως η g είναι συνεχής και παραγωγίσιμη στο (-οο,0) με πρώτη παράγωγο:
g΄(x)=(x-1)(e^(-x))

Για x>0 είναι g(x)=x(e^(-x)). Επομένως η g είναι συνεχής και παραγωγίσιμη στο (0,+oo) με πρώτη παράγωγο:
g΄(x)=(1-x)(e^(-x))

Είναι lim(x->0-)g(x)=lim(x->0-)[-x(e^(-x))]=-0*(e^(-0))=0 και lim(x->0+)g(x)=lim(x->0+)[x(e^(-x))]=0*(e^(-0))=0.
Επειδή lim(x->0-)g(x)=lim(x->0+)g(x)=0 τότε lim(x->0)g(x)=0
Επειδή lim(x->0)g(x)=g(0)=0 τότε η g είναι συνεχής στο 0. Άρα η g είναι συνεχής στο R.

Η g είναι συνεχής στο (-οο,0], παραγωγίσιμη στο (-οο,0) και ισχύει g΄(x)<0 για κάθε x στο (-οο,0). Επομένως η g είναι γνησίως φθίνουσα στο (-οο,0].
Η g είναι συνεχής στο [0,1], παραγωγίσιμη στο (0,1) και ισχύει g΄(x)>0 για κάθε x στο (0,1). Επομένως η g είναι γνησίως αύξουσα στο [0,1].
Η g είναι συνεχής στο [1,+οο), παραγωγίσιμη στο (1,+οο) και ισχύει g΄(x)<0 για κάθε x στο (1,+οο). Επομένως η g είναι γνησίως φθίνουσα στο [1,+οο).

Θέτουμε u=-x
lim(x->-oo)(-x)=+oo
lim(x->-oo)g(x)=lim(x->-oo)[(-x)*(e^(-x))]=lim(u->+oo)(u(e^u))=+oo επειδή lim(x->+oo)x=lim(x->+oo)(e^x)=+oo

Θεωρούμε τις συναρτήσεις h1(x)=x και h2(x)=e^x. Οι h1 και h2 είναι συνεχείς και παραγωγίσιμες στο R με πρώτες παραγώγους:
h1΄(x)=1
h2΄(x)=e^x

Έχουμε
lim(x->+oo)h1(x)=lim(x->+oo)x=+oo
lim(x->+oo)h2(x)=lim(x->+oo)(e^x)=+oo
lim(x->+oo)[h1΄(x)/h2΄(x)]=lim(x->+oo)(1/(e^x))=lim(x->+oo)(e^(-x))=0

Επειδή lim(x->+oo)h1(x)=lim(x->+oo)h2(x)=+oo και lim(x->+oo)[h1΄(x)/h2΄(x)]=0 τότε σύμφωνα με τον 2ο κανόνα De L' Hospital είναι lim(x->+oo)[h1(x)/h2(x)]=lim(x->+oo)[h1΄(x)/h2΄(x)]=0

Άρα lim(x->+oo)[x/(e^x)]=0 => lim(x->+oo)[x(e^(-x))]=0

Έχουμε lim(x->+oo)g(x)=lim(x->-oo)[x(e^(-x))]=0

Επειδή η g είναι συνεχής στο R, γνησίως φθίνουσα στο (-οο,0], γνησίως αύξουσα στο [0,1] και γνησίως φθίνουσα στο [1,+οο) τότε παρουσιάζει τοπικό ελάχιστο στο x1=0 με τιμή g(0)=0 και τοπικό μέγιστο στο x2=1 με τιμή g(1)=1/e

Συνοψίζοντας
g(0)=0
g(1)=1/e
lim(x->-oo)g(x)=+oo
lim(x->+oo)g(x)=0

Η g είναι συνεχής και γνησίως φθίνουσα στο (-οο,0], οπότε g((-oo,0])=[g(0),lim(x->-oo)g(x))=[0,+oo)
Η g είναι συνεχής και γνησίως αύξουσα στο [0,1], οπότε g([0,1])=[g(0),g(1)]=[0,1/e]
Η g είναι συνεχής και γνησίως φθίνουσα στο [1,+oo), οπότε g([1,+oo))=(lim(x->+oo)g(x),g(1)]=(0,1/e]

Παρατηρούμε ότι g(x)=0 μόνο για x=0
Για x>0 ισχύει g(x)<=g(1)=1/e

Άρα αν το πεδίο ορισμού της g είναι το (0,+οο) ή το [0,+οο) τότε η g έχει ολικό μέγιστο στο x0=1 με τιμή g(1)=1/e.
Σε αυτήν την περίπτωση το ζητούμενο σημείο είναι το M(1,f(1)) όπου f(1)=e^(-1)=1/e μονάδες μήκους και η μέγιστη τιμή του εμβαδού είναι maxE(Ω)=g(1)=1/e τετραγωνικές μονάδες μήκους.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[hliass_1989]

η εκφωνηση ηταν η παραπανω..απλα αν βρεις καποια, αιτιολογησε αν μπορεις το σκεπτικο λιγο, ευχαριστω.μπαρλας μαθηματια γενικης ειναι

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Guest 018946]

ρε ηλια οταν δινουμε ασκηση γραφουμε ακριβως την εκφωνηση που εδω δινεται οτι χ>0

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[aris-bas]

Στο 1ο όριο σκέφτηκα να διαιρεσω με χ αριθμητη κ παρονομαστή...
Στο 2 να λύσω ως προς f(x) κ g(x) αντίστοιχα

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Civilara]

View attachment 55170

Για κάθε x ανήκει R ισχύει -1<=ημx<=1. Για κάθε x>0 έχουμε:
-1<=ημx<=1 => -(1/x)<=ημx/x<=1/x

Είναι lim(x->+oo)(1/x)=0 => lim(x->+oo)[-(1/x)]=-0=0
Επειδή lim(x->+oo)(1/x)=lim(x->+oo)[-(1/x)]=0 τότε σύμφωνα με το κριτήριο παρεμβολής είναι lim(x->+oo)(ημx/x)=0

Για κάθε x ανήκει R ισχύει -1<=συνx<=1. Για κάθε x στο R* έχουμε:
-1<=συνx<=1 => -(1/(x^2))<=συνx/x<=1/(x^2)

Είναι lim(x->+oo)[1/(x^2)]=0 => lim(x->+oo)[-(1/(x^2))]=-0=0
Επειδή lim(x->+oo)[1/(x^2)]=lim(x->+oo)[-(1/(x^2))]=0 τότε σύμφωνα με το κριτήριο παρεμβολής είναι lim(x->+oo)[συνx/(x^2)]=0

Έχουμε
lim(x->+oo)[(2xημx+συνx)/SQRT((x^4)+1)]=lim(x->+oo){[2(ημx/x)+(συνx/(x^2))]/SQRT(1+(1/(x^4)))}=(2*0+0)/SQRT(1+0)=0

Άρα lim(x->+oo)[(2xημx+συνx)/SQRT((x^4)+1)]=0

View attachment 55171

Έχουμε

lim(x->0){[(SQRT((x^2)+1)-1)/(xημx)]f(x)g(x)}=lim(x->0){[f(x)/(xημx)][(SQRT((x^2)+1)-1)g(x)]}=
=lim(x->0)[f(x)/(xημx)]*lim(x->0)[(SQRT((x^2)+1)-1)g(x)]=3*5=15

Για x κοντά στο 0 έχουμε
f(x)g(x)={[(SQRT((x^2)+1)-1)/(xημx)]f(x)g(x)}*[(xημx)/(SQRT((x^2)+1)-1)]

Έχουμε
lim(x->0)[(x^2)/((SQRT((x^2)+1)-1))]=lim(x->0){[(x^2)(SQRT((x^2)+1)+1)]/[(SQRT((x^2)+1)-1)(SQRT((x^2)+1)+1)]}=
=lim(x->0){[(x^2)(SQRT((x^2)+1)+1)]/(x^2)}=lim(x->0)[SQRT((x^2)+1)+1]=SQRT((0^2)+1)+1=1+1=2

Συνεπώς
lim(x->0)[(xημx)/(SQRT((x^2)+1)-1)]=lim(x->0){(ημx/x)*[(x^2)/((SQRT((x^2)+1)-1))]}=1*2=2

Επομένως
lim(x->0)[f(x)g(x)]=lim(x->0){[(SQRT((x^2)+1)-1)/(xημx)]f(x)g(x)}*lim(x->0)[(xημx)/(SQRT((x^2)+1)-1)]=15*2=30

Άρα lim(x->0)[f(x)g(x)]=30

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[panabarbes]

View attachment 55170

View attachment 55171
Στο 1ο όριο σκέφτηκα να διαιρεσω με χ αριθμητη κ παρονομαστή...
Στο 2 να λύσω ως προς f(x) κ g(x) αντίστοιχα

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Civilara]

Πάνο αν μου επιτρέπεις έχεις ένα λάθος στο 2ο όριο. Στην τελευταία γραμμή θεωρείς ότι υπάρχει το lim(x->0)[f(x)g(x)] και το ξεχωρίζεις στον αριθμητή, κάτι που δεν το γνωρίζουμε εξαρχής.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[panabarbes]

Πάνο αν μου επιτρέπεις έχεις ένα λάθος στο 2ο όριο. Στην τελευταία γραμμή θεωρείς ότι υπάρχει το lim(x->0)[f(x)g(x)] και το ξεχωρίζεις στον αριθμητή, κάτι που δεν το γνωρίζουμε εξαρχής.

Θα έπρεπε να το δικαιολογήσω παραπάνω, αλλά εκείνη την ώρα δεν μπήκα στην διαδικασία!
Μπορούμε να καταλάβουμε ότι το όριο υπάρχει και είναι πραγματικός αριθμός, αν στην προτελευταία σειρά θέσουμε την συνάρτηση μέσα στο όριο και λύσουμε ως προς f(x)g(x) και, στη συνέχεια, περάσουμε όρια. Ακόμη και έτσι, το θεωρώ πιο γρήγορο τρόπο και ήθελα να τον προτείνω! Καλή παρατήρηση πάντως!

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[need4sheed]

ΔΙνεται η εξισωση h^2009+9x=10xh με αγνωστο τον h και x>1 Α)να αποδειξετε οτι η εξισωση εχει τρεις ακριβως ριζες h1(x),h2(x),h3(x) με h1(x)<h2(x)<1<h3(x)
β)να υπολογισετε τα ορια των h1(x),h2(x),h3(x) οταν το χ τεινει στο συν απειρο

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Lost in the Fog]

σας ευχαριστω πολυ για τη βοηθεια προηγουμενως . θα ηθελα μια ακομα βοηθεια στην παρακατω ασκηση:
Εστω οι μιγαδικοι z,w με και |w|=1
1] Αν και να αποδειξετε οτι ο t ειναι φανταστικος
2]Να βρειτε τον γεωμετρικο τοπο της εικονας του z
3] Nα βρειτε την μεγιστη και την ελαχιστη τιμη του |z|
4]Αν για τους μιγαδικους z1,z2 ισχυον οι σχεσεις να αποδειξετε οτι
το προβλημα μου ειναι το 1 και το 4. στο 1 οχ δεν ξερω απλως οταν παω να αντικαταστησω μετα απλως δεν καταληγω στη μορφη

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[panabarbes]

ΔΙνεται η εξισωση h^2009+9x=10xh με αγνωστο τον h και x>1 Α)να αποδειξετε οτι η εξισωση εχει τρεις ακριβως ριζες h1(x),h2(x),h3(x) με h1(x)<h2(x)<1<h3(x)
β)να υπολογισετε τα ορια των h1(x),h2(x),h3(x) οταν το χ τεινει στο συν απειρο

Μήπως στην αρχική σου σχέση είναι h(x) κι όχι απλώς h;

σας ευχαριστω πολυ για τη βοηθεια προηγουμενως . θα ηθελα μια ακομα βοηθεια στην παρακατω ασκηση:
Εστω οι μιγαδικοι z,w με και |w|=1
1] Αν και να αποδειξετε οτι ο t ειναι φανταστικος
2]Να βρειτε τον γεωμετρικο τοπο της εικονας του z
3] Nα βρειτε την μεγιστη και την ελαχιστη τιμη του |z|
4]Αν για τους μιγαδικους z1,z2 ισχυον οι σχεσεις να αποδειξετε οτι
το προβλημα μου ειναι το 1 και το 4. στο 1 οχ δεν ξερω απλως οταν παω να αντικαταστησω μετα απλως δεν καταληγω στη μορφη

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 11 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.