Βοήθεια/Aπορίες στα Μαθηματικά Προσανατολισμού

chester20080 · 1 Οκτωβρίου 2013

Αρχική Δημοσίευση από Maria_Spring:
Αν z ε C, να κάνετε γινόμενα πρωτοβάθμιων παραγόντων τα z^2 + 1 και z^4 +1
Μπορείς κανείς να με βοηθήσει; Σας παραθέτω παρακάτω το σκεπτικό μου για τη λύση
Για την πρώτη: z^2 + 1 = 0 --> z^2 = -1 ---> z^2 = i ^2 ---> z = i ή z = -i
άρα (z - i)(z+i) = 0
Για τη δεύτερη: z^4 +1 = 0 ---> z^4 = -1 ---> z^4 = - (i ^4) ---> z = - (-i) = i (διπλή) ή z = - i (διπλή)
άρα (z - i)^2 *(z+i)^2 = 0
Όμως, όταν έκανα Horner για τη δεύτερη, προέκυψε: (z+1)(z^3 - z^2+1)= 0 που δεν μου παραγοντοποιόταν περαιτέρω
Έχει κανείς καμιά άλλη πρόταση για τη δεύτερη; Νομίζω πως δεν είμαι σωστή! Ευχαριστώ εκ των προτέρων κάθε πρόθυμο/ πρόθυμη εθελοντή/εθελόντρια!

Οι ρίζες για το δεύτερο βγαίνουν ως εξής:z^4 +1=0<=>z^4-i^2=0<=>(z^2-i)(z^2+i=0<=>z=+-sqrt(2)/2 +- sqrt(2)i/,που προκύπτουν λύνοντας τη δευτεροβάθμια με διακρίνουσα,είτε με τύπους vieta είτε με αντικατάσταση z=x+yi,κλπ...

Αρχική Δημοσίευση από Maria_Spring:
Αν α,β, γ ε C, να λύσετε την εξίσωση αz^2 +βz + γ = 0 (α διάφορο του μηδενός) όταν z ε C
Καμία ιδέα κανείς;

Πρόχειρα έτσι όπως το λες προτείνω τύπους vieta και διακρίνουσα δ(αν η δ σου βγαίνει φανταστικός τότε προσπάθησε να εμφανίσεις σε αυτή το i με τη μορφή (1+i)^2=2i ενώ αν βγαίνει μιγαδικός η δ τότε ψάξε ποιός μιγαδικός στο τετράγωνο δίνει τη δ θέτοντας π.χ. w^2=δ με w=x+yi).

rebel · 1 Οκτωβρίου 2013

Αρχική Δημοσίευση από Maria_Spring:
Αν α,β, γ ε C, να λύσετε την εξίσωση αz^2 +βz + γ = 0 (α διάφορο του μηδενός) όταν z ε C
Καμία ιδέα κανείς;

Όπως και στην περίπτωση των πραγματικών αριθμών, με συμπλήρωση τετραγώνου φτάνουμε στην
$\left(z+\frac{b}{2a}\right)^2=\frac{b^2-4ac}{4a^2}$
Από κει και πέρα θέτοντας $x+yi=z+\frac{b}{2a}(*)$ και $u+vi=\frac{b^2-4ac}{4a^2}$ το πρόβλημα ανάγεται στην εύρεση $x,y \in \mathbb{R}$ τέτοια ώστε $(x+yi)^2=u+vi$ η οποία γίνεται

$x^2-y^2+2ixy=u+vi \Leftrightarrow \left. \begin{matrix} x^2-y^2=u \\ 2xy=v \end{matrix}\right\}$

Μετά την λύση του τελευταίου συστήματος τελικά προκύπτουν οι λύσεις

$x= \pm \sqrt{\frac{u+\sqrt{u^2+v^2}}{2}},\,\,y=\pm \frac{v}{|v|} \sqrt{\frac{-u+\sqrt{u^2+v^2}}{2}}$

και με αντικατάσταση στην σχέση (*) βρίσκουμε τις δύο τιμές του $z$ που ικανοποιούν την αρχική εξίσωση.

Συμπλήρωση: Οι παραπάνω λύσεις ισχύουν προφανώς για $v \neq 0$ . Για $v=0$ οι λύσεις απλουστεύουν και γίνονται $x= \pm \sqrt{u},\,\, y=0$ για $u \geq 0$ και $x=0,\,\,y= \pm \sqrt{-u}$ για $u<0$

patben · 01-10-13

Να βρεθεί ο z
$\frac{5-i}{1-3i}z-12i=\frac{9+13i}{3i-1}z+1$

chester20080 · 01-10-13

Αρχική Δημοσίευση από patben:
Να βρεθεί ο z
$\frac{5-i}{1-3i}z-12i=\frac{9+13i}{3i-1}z+1$

Το μόνο ιδιαίτερο στην άσκηση είναι να φέρεις τον όρο με το z από το δεύτερο μέλος στο πρώτο,να τραβήξεις το πρόσημο από τον παρονομαστή και να βγάλεις κοινό παράγοντα το z/(1-3i) και μετά να κάνεις τις πράξεις και να λύσεις ως προς z για να βγει z=313/170 - 159i/170.
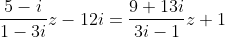
ΥΓ.:Γενικά να θυμάστε πως ο καλύτερος φίλος σας στα μαθηματικά είναι το wolframalpha!

panabarbes · 01-10-13

Αρχική Δημοσίευση από Maria_Spring:
Αν α,β, γ ε C, να λύσετε την εξίσωση αz^2 +βz + γ = 0 (α διάφορο του μηδενός) όταν z ε C
Καμία ιδέα κανείς;

Αρχική Δημοσίευση από styt_geia:
Όπως και στην περίπτωση των πραγματικών αριθμών, με συμπλήρωση τετραγώνου φτάνουμε στην
$\left(z+\frac{b}{2a}\right)^2=\frac{b^2-4ac}{4a^2}$
Από κει και πέρα θέτοντας $x+yi=z+\frac{b}{2a}(*)$ και $u+vi=\frac{b^2-4ac}{4a^2}$ το πρόβλημα ανάγεται στην εύρεση $x,y \in \mathbb{R}$ τέτοια ώστε $(x+yi)^2=u+vi$ η οποία γίνεται

$x^2-y^2+2ixy=u+vi \Leftrightarrow \left. \begin{matrix} x^2-y^2=u \\ 2xy=v \end{matrix}\right\}$

Μετά την λύση του τελευταίου συστήματος τελικά προκύπτουν οι λύσεις

$x= \pm \sqrt{\frac{u+\sqrt{u^2+v^2}}{2}},\,\,y=\pm \frac{v}{|v|} \sqrt{\frac{-u+\sqrt{u^2+v^2}}{2}}$

και με αντικατάσταση στην σχέση (*) βρίσκουμε τις δύο τιμές του $z$ που ικανοποιούν την αρχική εξίσωση.

Συμπλήρωση: Οι παραπάνω λύσεις ισχύουν προφανώς για $v \neq 0$ . Για $v=0$ οι λύσεις απλουστεύουν και γίνονται $x= \pm \sqrt{u},\,\, y=0$ για $u \geq 0$ και $x=0,\,\,y= \pm \sqrt{-u}$ για $u<0$

Oh boy, τόσο παρανοικό για πανελλήνιες. Μην σκοτίζεσαι τόσο με την άσκηση αυτή.

chester20080 · 01-10-13

Αρχική Δημοσίευση από panabarbes:
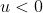
Oh boy, τόσο παρανοικό για πανελλήνιες. Μην σκοτίζεσαι τόσο με την άσκηση αυτή.

Συμφωνώ,αλλά ποτέ μη λες.ποτέ...Ιδίως όταν ήδη έχει μπει αυτό το ανεκδιήγητο φετινό Β3 σε συνθήκες πανελληνίων... :worry:

Ποιός ξέρει τι "διεστραμμένα" πράγματα θα βάλουν του χρόνου!

vimaproto · 02-10-13

Αρχική Δημοσίευση από Maria_Spring:
Αν z ε C, να κάνετε γινόμενα πρωτοβάθμιων παραγόντων τα z^2 + 1 και z^4 +1
Μπορείς κανείς να με βοηθήσει; Σας παραθέτω παρακάτω το σκεπτικό μου για τη λύση
Για την πρώτη: z^2 + 1 = 0 --> z^2 = -1 ---> z^2 = i ^2 ---> z = i ή z = -i
άρα (z - i)(z+i) = 0
Για τη δεύτερη: z^4 +1 = 0 ---> z^4 = -1 ---> z^4 = - (i ^4) ---> z = - (-i) = i (διπλή) ή z = - i (διπλή)
άρα (z - i)^2 *(z+i)^2 = 0
Όμως, όταν έκανα Horner για τη δεύτερη, προέκυψε: (z+1)(z^3 - z^2+1)= 0 που δεν μου παραγοντοποιόταν περαιτέρω
Έχει κανείς καμιά άλλη πρόταση για τη δεύτερη; Νομίζω πως δεν είμαι σωστή! Ευχαριστώ εκ των προτέρων κάθε πρόθυμο/ πρόθυμη εθελοντή/εθελόντρια!

Εγώ έκανα κάτι άλλο στη δεύτερη
${z}^{4}+1=0\Rightarrow {z}^{4}+2{z}^{2}-2{z}^{2}+1=0\Rightarrow {({z}^{2}+1)}^{2}=2{z}^{2}\Rightarrow {z}^{2}+1=\pm z\sqrt{2}$
Που είναι δύο δευτεροβάθμιες εξισώσεις ως προς Ζ με λύσεις
${z}_{1,2}=\frac{\sqrt{2}(-1\pm i)}{2},{z}_{3,4}=\frac{\sqrt{2}(1\pm i)}{2}$

chester20080 · 2 Οκτωβρίου 2013

Αρχική Δημοσίευση από vimaproto:
Εγώ έκανα κάτι άλλο στη δεύτερη
${z}^{4}+1=0\Rightarrow {z}^{4}+2{z}^{2}-2{z}^{2}+1=0\Rightarrow {({z}^{2}+1)}^{2}=2{z}^{2}\Rightarrow {z}^{2}+1=\pm z\sqrt{2}$
Που είναι δύο δευτεροβάθμιες εξισώσεις ως προς Ζ με λύσεις
${z}_{1,2}=\frac{\sqrt{2}(-1\pm i)}{2},{z}_{3,4}=\frac{\sqrt{2}(1\pm i)}{2}$

Το αποτέλεσμα σωστό είναι.Έχω όμως μια γενική απορία:Υφίσταται ρίζα μιγαδικού?Δηλαδή είναι σωστό να γράφουμε sqrt(z)
ή sqrt(z^2) όταν z ή z^2 μιγαδικός?Δηλαδή ποιό το νόημα να πούμε sqrt(2+3i) π.χ..Κάτι τέτοιο θυμάμαι από το φροντιστήριο...

Guest 018946 · 02-10-13

που το ειδατε ρε παιδια το παρανοικο ; ηθελε καμια τρομερη εμπνευση μην τρελαθουμε τωρα δλδ

chester20080 · 02-10-13

Αρχική Δημοσίευση από dr.tasos:
που το ειδατε ρε παιδια το παρανοικο ; ηθελε καμια τρομερη εμπνευση μην τρελαθουμε τωρα δλδ

Αν εννοείς αυτό με τη λύση της δευτεροβάθμιας με μιγαδικούς συντελεστές το περίεργο πιθανόν να είναι γιατί κάποιος να κάνει όλη αυτή τη διαδικασία και να μην το καθαρίσει με τύπους του vieta φερ'ειπείν...

Guest 018946 · 02-10-13

γιατι δεν ξερει αν ισχυουν οι τυποι βιετα με μιγαδικους συντελεστες

chester20080 · 02-10-13

Αρχική Δημοσίευση από dr.tasos:
γιατι δεν ξερει αν ισχυουν οι τυποι βιετα με μιγαδικους συντελεστες

Κι όμως,ισχύουν!Ασχέτως αν δεν το αναφέρει το σχολικό.

vimaproto · 02-10-13

Αρχική Δημοσίευση από chester20080:
Το αποτέλεσμα σωστό είναι.Έχω όμως μια γενική απορία:Υφίσταται ρίζα μιγαδικού?Δηλαδή είναι σωστό να γράφουμε sqrt(z)
ή sqrt(z^2) όταν z ή z^2 μιγαδικός?Δηλαδή ποιό το νόημα να πούμε sqrt(2+3i) π.χ..Κάτι τέτοιο θυμάμαι από το φροντιστήριο...

Αν κατάλαβα την απορία σου οι δύο διαδοχικές σελίδες από το πανεπιστημιακό βιβλίο Ι. ΑΝΑΣΤΑΣΙΑΔΗ - Σ. ΜΠΑΛΛΗ στα συνημμένα , ίσως σε ικανοποιούν.

Guest 018946 · 02-10-13

Ειναι γνωστο απο την θεωρια ( δεν ξερω , ρωταω ) ;

chester20080 · 2 Οκτωβρίου 2013

Αρχική Δημοσίευση από dr.tasos:
Ειναι γνωστο απο την θεωρια ( δεν ξερω , ρωταω ) ;

Βασικά στο σχολικό δεν αναφέρεται καν αν ισχύουν ή όχι σε μια τέτοια περίπτωση,αλλά στο φροντιστήριο μας είχαν πει να το χρησιμοποιούμε σαν κάτι δεδομένο.

Αρχική Δημοσίευση από vimaproto:
Αν κατάλαβα την απορία σου οι δύο διαδοχικές σελίδες από το πανεπιστημιακό βιβλίο Ι. ΑΝΑΣΤΑΣΙΑΔΗ - Σ. ΜΠΑΛΛΗ στα συνημμένα , ίσως σε ικανοποιούν.

Δηλαδή υφίσταται τελικά ρίζα μιγαδικού και αυτοί είναι οι τύποι/διαδικασία για να την υπολογίσεις?Όμως γιατί στο φροντ. μας έλεγαν ότι δεν μπορούμε να γράψουμε sqrt(μιγαδικός) γιατί είναι λάθος?Και επίσης με προβλημάτισε αυτό εδώ:
https://ischool.e-steki.gr/showthread.php?t=40119https://ischool.e-steki.gr/showthread.php?t=40119
Διάβασε μέχρι και post #16.

vimaproto · 02-10-13

Για να χαλαρώσουμε και λίγο. Τι να βάλω μεταξύ του post #10 και των συνημμένων? 1, Χ ή 2?
Στο #10 έχει και Σημείωση¨Διαβάστε την . Το μήνυμα αυτό γράφτηκε πάνω από 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

chester20080 · 02-10-13

Αρχική Δημοσίευση από vimaproto:
Για να χαλαρώσουμε και λίγο. Τι να βάλω μεταξύ του post #10 και των συνημμένων? 1, Χ ή 2?
Στο #10 έχει και Σημείωση¨Διαβάστε την . Το μήνυμα αυτό γράφτηκε πάνω από 5 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

Μάλλον 2...Οπότε έχεις δίκιο,ορίζεται και υπολογίζεται μιγαδικός σε υπόρριζο.Όμως είναι στην ύλη των πανελληνίων?Γιατί μας έλεγαν άλλα στο φρο?

rebel · 2 Οκτωβρίου 2013

Απ' ότι κατάλαβα η διαμάχη γίνεται για το αν έχει νόημα το σύμβολο $\sqrt[\nu]{\color{white}{x} }$ όταν το υπόριζο είναι κάτι άλλο πέρα από μη αρνητικός πραγματικός. Και εδώ οι απόψεις διίστανται. Στο πανεπιστημιακό βιβλίο που παραπέμπει ο vimaproto, o συγγραφέας δεν έχει πρόβλημα να βάλει υπόριζο μιγαδικό. Απ' την άλλη σ' αυτό το άρθρο ο συγγραφέας διαχωρίζει τις έννοιες ν-οστή ρίζα ενός αριθμού και σύμβολο $\sqrt[\nu]{\color{white}{x} }$ . Προτιμάει να κρατάει το δεύτερο μόνο για υπόριζα μη αρνητικούς πραγματικούς (Δείτε την σημείωση 2 σελ. 3 του άρθρου). Για τα σχολικά μαθηματικά και προς αποφυγή παρεξηγήσεων προσωπικά θα προτιμούσα αυτή την προσέγγιση. Ίσως chester αυτόν τον διαχωρισμό έκανε ο καθηγητής σου στο φροντιστήριο.

Dafni16 · 02-10-13

Boήθεια!!!1) f(z)= 2+iz/1-z συζυγές, z#1...ν.δ.ο (f(2))^2004 ΕR.....2)Aν ο z κινείται σε κύκλο με κέντρο 0(0,0) και ακτίνα ρ=2 και w=z+1/z ν.δ.ο οι εικόνες του w κινούνται σε έλλειψη.....3) |z+i|=|z+2| με z=(χ-2) + (ψ-1) i....Να βρεθεί ο γ.τ των σημείων Μ(χ,ψ)

chester20080 · 2 Οκτωβρίου 2013

Αρχική Δημοσίευση από Dafni16:
Boήθεια!!!1) f(z)= 2+iz/1-z συζυγές, z#1...ν.δ.ο (f(2))^2004 ΕR.....2)Aν ο z κινείται σε κύκλο με κέντρο 0(0,0) και ακτίνα ρ=2 και w=z+1/z ν.δ.ο οι εικόνες του w κινούνται σε έλλειψη.....3) |z+i|=|z+2| με z=(χ-2) + (ψ-1) i....Να βρεθεί ο γ.τ των σημείων Μ(χ,ψ)

Επειδή τα έκανα στα γρήγορα συγχωρέστε τυχόν λάθη...
1)Αν z=2 τότε z συζυγής =2,άρα άμα θέσω όπου z=2 στη σχέση προκύπτει f(2)=-2-2i=-2(1+i).Τότε (f(2))^2004=2^2004*[(1+i)^2]^1002=2^2004*(2i)^1002=...=-2^3006 ER
2)Έστω z=α+βi και w=x+yi.Αφού ο z κινείται στον κύκλο ισχύει α^2+β^2=4 (1)
w=z+1/z<=>x+yi=α+βi+1/(α+βi)=α+βi+(α-βi)/(α^2+β^2)=(από (1)) α+βi+(α-βi)/4<=>...<=>4x+4yi=5α+3βi<=>4x=5α και 4y=3β ] <=>α^2=16x^2/25 και β^2=16y^2/9 άρα η έλλειψη είναι 4x^2/25+4y^2/9=1
3)Υψώνω στο τετράγωνο κατά μέλη,η γνωστή ιδιότητα z απόλυτο^2=z*z συζυγής,όλα στο δεύτερο μέλος,βγάζουμε κοινούς παράγοντες ώστε να εμφανιστούν τα z+-z συζυγής και μετά από πράξεις καταλήγουμε σε 4x-2y-3=0.

Βοήθεια/Aπορίες στα Μαθηματικά Προσανατολισμού

Διακεκριμένο μέλος

Πολύ δραστήριο μέλος

Νεοφερμένος

Διακεκριμένο μέλος

Εκκολαπτόμενο μέλος

Διακεκριμένο μέλος

Πολύ δραστήριο μέλος

Διακεκριμένο μέλος

Guest 018946

Επισκέπτης

Διακεκριμένο μέλος

Guest 018946

Επισκέπτης

Διακεκριμένο μέλος

Πολύ δραστήριο μέλος

Συνημμένα

Guest 018946

Επισκέπτης

Διακεκριμένο μέλος

Πολύ δραστήριο μέλος

Διακεκριμένο μέλος

Πολύ δραστήριο μέλος

Νεοφερμένος

Διακεκριμένο μέλος