Βοήθεια/Aπορίες στα Μαθηματικά Προσανατολισμού

[rebel]

Η ανισότητα μυρίζει κριτήριο παρεμβολής. Θυμήσου και την προηγούμενη άσκησή σου, την 1 εδώ

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Civilara]

Οι συναρτησεις f,g,h εχουν κοινο πεδιο ορισμου Α για καθε χΕΑ ισχυει g(x)<=f(x)<=h(x)
για το σημειο xoεA ισχυουν
g(xo)=f(xo)=h(xo) και g'(xo)=h'(xo) =a
ν.δ.ο η f ειναι παραγωγισιμη στο χο και ειναι f'(xo)=α
μια βοηθεια λιγο σε αυτη την ασκσηση

Διακρίνονται 3 περιπτώσεις:
α) υπάρχουν γ,δ ανήκουν R τέτοια ώστε γ<x0<δ και (γ,δ) υποσύνολο Α
β) υπάρχει γ ανήκει R με γ<x0 ώστε (γ,x0] υποσύνολο Α και δεν υπάρχει κανένα δ ανήκει R με δ>x0 ώστε το [x0,δ) να είναι υποσύνολο του Α
γ) δεν υπάρχει κανένα γ ανήκει R με γ<x0 ώστε (γ,x0] υποσύνολο Α και υπάρχει δ ανήκει R με δ>x0 ώστε το [x0,δ) να είναι υποσύνολο του Α

Θα εξεταστεί η περίπτωση α) όπου παίρνουμε υπόψη και τα δύο πλευρικά όρια. Στις περιπτώσεις β) και γ) το όριο συμπίπτει με το ένα από τα δύο πλευρικά όρια της περίπτωσης α) όταν το x τείνει στο 0.

Έστω g(x0)=f(x0)=h(x0)=b. Ξέρουμε ότι g΄(x0)=h΄(x0)=a. Από τον ορισμό της παραγώγου έχουμε τα εξής:

lim(x->x0)((g(x)-g(x0))/(x-x0))=g΄(x0) <=> lim(x->x0)((g(x)-b)/(x-x0))=a <=> lim(x->x0-)((g(x)-b)/(x-x0))=lim(x->x0+)((g(x)-b)/(x-x0))=a
lim(x->x0)((h(x)-h(x0))/(x-x0))=h΄(x0) <=> lim(x->x0)(h(x)-b)/(x-x0))=a <=> lim(x->x0-)((h(x)-b)/(x-x0))=lim(x->x0+)(h(x)-b)/(x-x0))=a

g(x)<=f(x)<=h(x) <=> g(x)-b<=f(x)-b<=h(x)-b

Αν x>x0 τότε x-x0>0, οπότε παίρνουμε:

(g(x)-b)/(x-x0)<=(f(x)-b)/(x-x0)<=(h(x)-b)/(x-x0)

lim(x->x0+)((g(x)-b)/(x-x0))=lim(x->x0+)((h(x)-b)/(x-x0))=a
Επομένως σύμφωνα με το κριτήριο παρεμβολής προκύπτει lim(x->x0+)((f(x)-b)/(x-x0))=a

Αν x<x0 τότε x-x0<0, οπότε παίρνουμε:

(h(x)-b)/(x-x0)<=(f(x)-b)/(x-x0)<=(g(x)-b)/(x-x0)

lim(x->x0-)((h(x)-b)/(x-x0))=lim(x->x0-)((g(x)-b)/(x-x0))=a
Επομένως σύμφωνα με το κριτήριο παρεμβολής προκύπτει lim(x->x0-)((f(x)-b)/(x-x0))=a

Συνεπώς:

lim(x->x0-)((f(x)-b)/(x-x0))=lim(x->x0+)((f(x)-b)/(x-x0))=a <=> lim(x->x0)((f(x)-b)/(x-x0))=a

Θα εξεταστεί αν η f είναι παραγωγίσιμη στο x0. Έχουμε:

lim(x->x0)(((f(x)-f(x0))/(x-x0))=lim(x->x0)((f(x)-b)/(x-x0))=a όπως έχει βρεθεί. Συνεπώς η f είναι παραγωγίσιμη στο x0 με πρώτη παράγωγο f΄(x0)=a

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[muga no 2]

ΚΑΛΗΜΕΡΑ ΠΑΙΔΙΑ!!
Με αφορμή μια άσκηση σε ενα βοήθημα θα ήθελα να ρωτήσω όταν μας δίνουν το πεδίο ορισμού μιας συνάρτησης χωρίς όμως κάποιο άλλο στοιχείο όπως ο τύπος ή η γραφική παράστασή της και μας ρωτάνε αν είνε γνησίως αύξουσα ή φθίνουσα τι πρέπει να κάνω;;;

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Χαρουλιτα]

Mπορεις να μας πεις την ασκηση???

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Aris90]

Διακρίνονται 3 περιπτώσεις:
α) υπάρχουν γ,δ ανήκουν R τέτοια ώστε γ<x0<δ και (γ,δ) υποσύνολο Α
β) υπάρχει γ ανήκει R με γ<x0 ώστε (γ,x0] υποσύνολο Α και δεν υπάρχει κανένα δ ανήκει R με δ>x0 ώστε το [x0,δ) να είναι υποσύνολο του Α
γ) δεν υπάρχει κανένα γ ανήκει R με γ<x0 ώστε (γ,x0] υποσύνολο Α και υπάρχει δ ανήκει R με δ>x0 ώστε το [x0,δ) να είναι υποσύνολο του Α

Θα εξεταστεί η περίπτωση α) όπου παίρνουμε υπόψη και τα δύο πλευρικά όρια. Στις περιπτώσεις β) και γ) το όριο συμπίπτει με το ένα από τα δύο πλευρικά όρια της περίπτωσης α) όταν το x τείνει στο 0.

Έστω g(x0)=f(x0)=h(x0)=b. Ξέρουμε ότι g΄(x0)=h΄(x0)=a. Από τον ορισμό της παραγώγου έχουμε τα εξής:

lim(x->x0)((g(x)-g(x0))/(x-x0))=g΄(x0) <=> lim(x->x0)((g(x)-b)/(x-x0))=a <=> lim(x->x0-)((g(x)-b)/(x-x0))=lim(x->x0+)((g(x)-b)/(x-x0))=a
lim(x->x0)((h(x)-h(x0))/(x-x0))=h΄(x0) <=> lim(x->x0)(h(x)-b)/(x-x0))=a <=> lim(x->x0-)((h(x)-b)/(x-x0))=lim(x->x0+)(h(x)-b)/(x-x0))=a

g(x)<=f(x)<=h(x) <=> g(x)-b<=f(x)-b<=h(x)-b

Αν x>x0 τότε x-x0>0, οπότε παίρνουμε:

(g(x)-b)/(x-x0)<=(f(x)-b)/(x-x0)<=(h(x)-b)/(x-x0)

lim(x->x0+)((g(x)-b)/(x-x0))=lim(x->x0+)((h(x)-b)/(x-x0))=a
Επομένως σύμφωνα με το κριτήριο παρεμβολής προκύπτει lim(x->x0+)((f(x)-b)/(x-x0))=a

Αν x<x0 τότε x-x0<0, οπότε παίρνουμε:

(h(x)-b)/(x-x0)<=(f(x)-b)/(x-x0)<=(g(x)-b)/(x-x0)

lim(x->x0-)((h(x)-b)/(x-x0))=lim(x->x0-)((g(x)-b)/(x-x0))=a
Επομένως σύμφωνα με το κριτήριο παρεμβολής προκύπτει lim(x->x0-)((f(x)-b)/(x-x0))=a

Συνεπώς:

lim(x->x0-)((f(x)-b)/(x-x0))=lim(x->x0+)((f(x)-b)/(x-x0))=a <=> lim(x->x0)((f(x)-b)/(x-x0))=a

Θα εξεταστεί αν η f είναι παραγωγίσιμη στο x0. Έχουμε:

lim(x->x0)(((f(x)-f(x0))/(x-x0))=lim(x->x0)((f(x)-b)/(x-x0))=a όπως έχει βρεθεί. Συνεπώς η f είναι παραγωγίσιμη στο x0 με πρώτη παράγωγο f΄(x0)=a

σε ευχαριστω για την βοηθεια

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[αδαμαντια52071]

Στις συνεπειες του θ.μ.τ οταν μας δινεται μια σχεση και μας ζητα τον τυπο της f
και με τα πολλα καταληγουμε οτι η παραγωγος μιας συναρτησης εινα ιση με την συναρτηση
δηλ

[ln|X|]' = ln|X| μετα πως προχωραμε?

Εννοω πως θα εισαγουμε την σταθερα c ?

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Civilara]

Στις συνεπειες του θ.μ.τ οταν μας δινεται μια σχεση και μας ζητα τον τυπο της f
και με τα πολλα καταληγουμε οτι η παραγωγος μιας συναρτησης εινα ιση με την συναρτηση
δηλ

[ln|X|]' = ln|X| μετα πως προχωραμε?

Εννοω πως θα εισαγουμε την σταθερα c ?

Η άγνωστη συνάρτηση f ικανοποιεί την διαφορική εξίσωση f΄(x)=f(x) στο διάστημα

Θεωρούμε την συνάρτηση g με τύπο g(x)=f(x)(e^(-x)), x ανήκει Δ. Επειδή η f είναι συνεχής και παραγωγίσιμη στο Δ, τότε και η g είναι συνεχής και παραγωγίσιμη στο Δ με πρώτη παράγωγο g΄(x)=f΄(x)(e^(-x))-f(x)(e^(-x))=(f΄(x)-f(x))(e^(-x))

Επειδή f΄(x)=f(x) για κάθε x στο εσωτερικό του Δ τότε ισχύει g΄(x)=0 για κάθε x στο Δ

Άρα η g είναι συνεχής στο Δ, παραγωγίσιμη στο εσωτερικό του Δ και ισχύει g΄(x)=0 για κάθε x στο εσωτερικό του Δ. Επομένως υπάρχει σταθερά c ανήκει R ώστε g(x)=c για κάθε x ανήκει Δ. Επομένως:

g(x)=c <=> f(x)(e^(-x))=c <=> f(x)=c(e^x) για κάθε x ανήκει Δ

Αυτός ο τύπος της f ισχύει σε διάστημα. Αν η διαφορική εξίσωση ικανοποιείται σε σύνολο Α που δεν είναι διάστημα αλλά αποτελείται από ένωση διαστημάτων Δn όπου n=1,2,...,N έτσι ώστε η f να είναι παραγωγίσιμη στα Δn (των οποίων η τομή ανά δύο είναι το μηδενικό σύνολο, δηλαδή τα Δn δεν έχουν κοινά στοιχεία) τότε σε κάθε διάστημα Δn υπάρχει πραγματική σταθερά cn ώστε
g(x)=cn <=> f(x)=cn(e^x)

Οι σταθερές c1, c2, ..., cN δεν είναι απαραίτητα ίσες μεταξύ τους

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Guest 278211]

Στις συνεπειες του θ.μ.τ οταν μας δινεται μια σχεση και μας ζητα τον τυπο της f
και με τα πολλα καταληγουμε οτι η παραγωγος μιας συναρτησης εινα ιση με την συναρτηση
δηλ

[ln|X|]' = ln|X| μετα πως προχωραμε?

Εννοω πως θα εισαγουμε την σταθερα c ?

Υπάρχουν διάφοροι τρόποι. Ένας από αυτούς είναι στη σελ 252, οπότε γράφω έναν άλλο:
Θέτουμε: K(x)=ln|x| οπότε η εξίσωση γίνεται: K'(x)=K(x)
Έπειτα πολλαπλασιάζουμε με
δηλαδή θα έχουμε:
ή διαφορετικά:
επομένως: ή
(μέθοδος που περιγράφεται στη σελ 322, εκτός ύλης αλλά πολύ χρήσιμη, την έχουν όλα τα βοηθήματα.)

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[αδαμαντια52071]

Ευχαριστω παρα πολυ!

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Polymnia]

Εννοείς ότι δεν καταλαβαίνεις την λογική με την οποία θεωρήσαμε την συνάρτηση ; Είδα ότι Bolzano για την σε κλειστό διάστημα με άκρα ρίζες των f,g δεν οδηγεί πουθενά αφού δεν έχω πληροφορίες για το πρόσημό των f,g. Αναρωτιέμαι λοιπόν, υπάρχει άλλη συνάρτηση για την οποία η ύπαρξη ρίζας συνεπάγεται ύπαρξη ρίζας για την ; Όμως το δεδομένο καταδεικνύει ότι αν υπάρχει ρίζα για την -που είναι πιο εύκολο να χρησιμοποιηθεί λόγω των τετραγώνων- τότε αυτή η ρίζα θα είναι υποχρεωτικά ρίζα της . Δες το και αλλιώς. Αν έχεις δύο πραγματικούς και ξέρεις ότι με τότε υποχρεωτικά

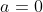
Όσο για το Bolzano, δεν χρειάζεται να πάρουμε περιπτώσεις. Η ανισότητα είναι γνήσια αρνητική διότι αφενός το δεν μπορεί να είναι ρίζα και της , αφετέρου το δεν μπορεί να είναι ρίζα και της . Αν συνέβαινε οποιοδήποτε από τα δύο, αυτό θα ερχόταν σε αντίθεση με την υπόθεση ότι .

Πολύ αναλυτική εξήγηση ,ένα μεγάλο ευχαριστώ για αυτό !!!!!! ελπίζω να μην έγινα ενοχλητική

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[mary-blackrose]

1)δειξτε οτι lnx<=x-1
2)Aν f(x)ημχ+χ>=0,δειξτε οτι f(0)=-1
3)Aν α>β>0,δειξτε οτι e^(α-β) > 1+α/1+β
4)Αν f(x)>=x+1 και η f διερχεται απο το (0,1),να βρεθει το f'(0).

υ.γ γνωριζω τη μεθοδολογια οπου τα φερνω ολα στο πρωτο μελος και μετα θετω(π,χ. οπως η ασκηση 1)...αλλα κολλαω στη συνεχεια και δεν ξερω τι να κανω..
καμια βοηθεια/ιδεα κανεις???

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[φρι]

Να βρεθει το lim(x-->1+)[ ln(lnx) ]

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[φρι]

1)δειξτε οτι lnx<=x-1
2)Aν f(x)ημχ+χ>=0,δειξτε οτι f(0)=-1
3)Aν α>β>0,δειξτε οτι e^(α-β) > 1+α/1+β
4)Αν f(x)>=x+1 και η f διερχεται απο το (0,1),να βρεθει το f'(0).

υ.γ γνωριζω τη μεθοδολογια οπου τα φερνω ολα στο πρωτο μελος και μετα θετω(π,χ. οπως η ασκηση 1)...αλλα κολλαω στη συνεχεια και δεν ξερω τι να κανω..
καμια βοηθεια/ιδεα κανεις???

Σε ποιο κεφαλαιο εισαι?

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[mary-blackrose]

Σε ποιο κεφαλαιο εισαι?

στη μονοτονια-ακροτατα,συνεπειες θεωρηματος rolle...

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[φρι]

Οκ,συγνωμη που δε μπορω να σε βοηθησω γτ τρ μπηκα ρολ!

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[mary-blackrose]

Οκ,συγνωμη που δε μπορω να σε βοηθησω γτ τρ μπηκα ρολ!

δεν πειραζει βρε..σε ευχαριστω παντως που ενδιαφερθηκες!!!

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Civilara]

1)δειξτε οτι lnx<=x-1
2)Aν f(x)ημχ+χ>=0,δειξτε οτι f(0)=-1
3)Aν α>β>0,δειξτε οτι e^(α-β) > 1+α/1+β
4)Αν f(x)>=x+1 και η f διερχεται απο το (0,1),να βρεθει το f'(0).

υ.γ γνωριζω τη μεθοδολογια οπου τα φερνω ολα στο πρωτο μελος και μετα θετω(π,χ. οπως η ασκηση 1)...αλλα κολλαω στη συνεχεια και δεν ξερω τι να κανω..
καμια βοηθεια/ιδεα κανεις???

1) Θεωρούμε την συνάρτηση f(x)=x-lnx με πεδίο ορισμού το A=(0,+oo).

Η f είναι συνεχής και παραγωγίσιμη στο (0,+οο) με πρώτη παράγωγο f΄(x)=1-(1/x)=(x-1)/x, x>0. Παρατηρούμε ότι f΄(1)=0 και η εξίσωση f΄(x)=0 δεν έχει άλλη λύση.

Η συνάρτηση f είναι συνεχής στο (0,1], παραγωγίσιμη στο (0,1) και ισχύει f΄(x)<0 για κάθε x στο (0,1). Επομένως η f είναι γνησίως φθίνουσα στο (0,1]. Η συνάρτηση f είναι συνεχής στο [1,+οο), παραγωγίσιμη στο (1,+οο) και ισχύει f΄(x)>0 για κάθε x στο (1,+οο). Επομένως η f είναι γνησίως αύξουσα στο [1,+οο).

Συνεπώς η f παρουσιάζει ολικό ελάχιστο στο x0=1 με τιμή f(1)=1. Άρα για κάθε x ανήκει (0,+οο) έχουμε:

f(x)>=f(1) <=> x-lnx>=1 <=> lnx<=x-1

2) Επειδή δεν δίνεται το πεδίο ορισμού της f θεωρείται ότι υπάρχουν πραγματικοί αριθμοί α,β τέτοιοι ώστε -π<=α<0<β<=π ώστε η f να είναι ορισμένη στο (α,β) και ότι η f είναι συνεχής στο x0=0. Συνεπώς για κάθε x ανήκει (α,β) ισχύει f(x)ημx+x>=0 <=> f(x)ημx>=-x

Γνωρίζουμε ότι lim(x->0)(ημx/x)=1. Συνεπώς lim(x->0)(x/ημx)=1/lim(x->0)(ημx/x)=1/1=1. Συνεπώς

lim(x->0)(x/ημx)=1 <=> lim(x->0-)(x/ημx)=lim(x->0+)(x/ημx)=1

Επειδή η f είναι συνεχής στο x0 και ορισμένη στα διαστήματα (α,0], [0,β) τότε ισχύει η ισοδυναμία:

lim(x->0)f(x)=f(0) <=> lim(x->0-)f(x)=lim(x->0+)f(x)=f(0)

Αν x ανήκει (α,0) τότε ισχύει ημx<0 αφού ισχύει ημx<0 για κάθε x ανήκει (-π,0). Άρα τότε προκύπτει:
f(x)ημx>=-x => f(x)<=-(x/ημx) => lim(x->0-)f(x)<=-lim(x->0-)(x/ημx) => f(0)<=-1

Αν x ανήκει (0,β) τότε ισχύει ημx>0 αφού ισχύει ημx>0 για κάθε x ανήκει (0,π). Άρα τότε προκύπτει:
f(x)ημx>=-x => f(x)>=-(x/ημx) => lim(x->0+)f(x)>=-lim(x->0+)(x/ημx) => f(0)>=-1

Από τις σχέσεις f(0)<=-1 και f(0)>=-1 προκύπτει ότι f(0)=-1


3) Θεωρούμε την συνάρτηση f(x)=(e^x)/(x+1) με πεδίο ορισμού το Α=(-οο,-1)U(-1,+οο)

Η f είναι συνεχής και παραγωγίσιμη στο Α με πρώτη παράγωγο:
f΄(x)=((e^x)΄(x+1)-(e^x)(x+1)΄)/((x+1)^2)=((e^x)(x+1)-(e^x))/((x+1)^2)=(x(e^x))/((x+1)^2)

Παρατηρούμε ότι f΄(0)=0 και η εξίσωση f΄(x)=0 δεν έχει άλλη λύση.

Η συνάρτηση f είναι συνεχής στο [0,+οο), παραγωγίσιμη στο (0,+οο) και για κάθε x στο (0,+οο) ισχύει f΄(x)>0. Άρα η f είναι γνησίως αύξουσα στο [0,+οο).

Επομένως για α>β>0 θα ισχύει f(α)>f(β) καθώς η f είναι γνησίως αύξουσα στο [0,+οο). Έτσι λοιπόν έχουμε:

α>β>0 => f(α)>f(β) => (e^α)/(α+1)>(e^β)/(β+1) => (e^α)/(e^β)>(α+1)/(β+1) => e^(α-β)>(1+α)/(1+β)


4) f(x)>=x+1
Η Cf διέρχεται από το (0,1) => f(0)=1
Επειδή δεν δίνεται το πεδίο ορισμού της f, θεωρούμε ότι υπάρχουν α,β ανήκουν R με α<0<β ώστε η f να είναι ορισμένη στο (α,β) και για κάθε x στο (α,β) να ισχύει f(x)>=x+1. Παρατηρούμε ότι για x=0 η ανισότητα γίνεται f(0)>=1 που ικανοποιείται αφού f(0)=1.

Δεν δίνεται στην εκφώνηση αλλά πρέπει να γνωρίζουμε ότι η f είναι παραγωγίσιμη στο 0. Επειδή λοιπόν η f είναι παραγωγίσιμη στο 0 τότε προκύπτει:

f΄(0)=lim(x->0)(((f(x)-f(0))/(x-0))=lim(x->0)((f(x)-1)/x)

Επειδή η f ορίζεται στα διαστήματα (α,0), (0,β) τότε ισχύει η ισοδυναμία:

lim(x->0)((f(x)-1)/x)=f΄(0) <=> lim(x->0-)((f(x)-1)/x)=lim(x->0+)((f(x)-1)/x)=f΄(0)


Έχουμε

f(x)>=x+1 => f(x)-1>=x για κάθε x στο (α,β)

Για x στο (α,0) είναι x<0, οπότε
(f(x)-1)/x<=1 => lim(x->0-)[(f(x)-1)/x)<=lim(x->0-)1 => f΄(0)<=1

Για x στο (β,0) είναι x>0, οπότε
(f(x)-1)/x>=1 => lim(x->0+)[(f(x)-1)/x)>=lim(x->0+)1 => f΄(0)>=1

Από τις σχέσεις f΄(0)<=1 και f΄(0)>=1 προκύπτει ότι f΄(0)=1

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[mary-blackrose]

1) Θεωρούμε την συνάρτηση f(x)=x-lnx με πεδίο ορισμού το A=(0,+oo).

Η f είναι συνεχής και παραγωγίσιμη στο (0,+οο) με πρώτη παράγωγο f΄(x)=1-(1/x)=(x-1)/x, x>0. Παρατηρούμε ότι f΄(1)=0 και η εξίσωση f΄(x)=0 δεν έχει άλλη λύση.

Η συνάρτηση f είναι συνεχής στο (0,1], παραγωγίσιμη στο (0,1) και ισχύει f΄(x)<0 για κάθε x στο (0,1). Επομένως η f είναι γνησίως φθίνουσα στο (0,1]. Η συνάρτηση f είναι συνεχής στο [1,+οο), παραγωγίσιμη στο (1,+οο) και ισχύει f΄(x)>0 για κάθε x στο (1,+οο). Επομένως η f είναι γνησίως αύξουσα στο [1,+οο).

Συνεπώς η f παρουσιάζει ολικό ελάχιστο στο x0=1 με τιμή f(1)=1. Άρα για κάθε x ανήκει (0,+οο) έχουμε:

f(x)>=f(1) <=> x-lnx>=1 <=> lnx<=x-1

2) Επειδή δεν δίνεται το πεδίο ορισμού της f θεωρείται ότι υπάρχουν πραγματικοί αριθμοί α,β τέτοιοι ώστε -π<=α<0<β<=π ώστε η f να είναι ορισμένη στο (α,β) και ότι η f είναι συνεχής στο x0=0. Συνεπώς για κάθε x ανήκει (α,β) ισχύει f(x)ημx+x>=0 <=> f(x)ημx>=-x

Γνωρίζουμε ότι lim(x->0)(ημx/x)=1. Συνεπώς lim(x->0)(x/ημx)=1/lim(x->0)(ημx/x)=1/1=1. Συνεπώς

lim(x->0)(x/ημx)=1 <=> lim(x->0-)(x/ημx)=lim(x->0+)(x/ημx)=1

Επειδή η f είναι συνεχής στο x0 και ορισμένη στα διαστήματα (α,0], [0,β) τότε ισχύει η ισοδυναμία:

lim(x->0)f(x)=f(0) <=> lim(x->0-)f(x)=lim(x->0+)f(x)=f(0)

Αν x ανήκει (α,0) τότε ισχύει ημx<0 αφού ισχύει ημx<0 για κάθε x ανήκει (-π,0). Άρα τότε προκύπτει:
f(x)ημx>=-x => f(x)<=-(x/ημx) => lim(x->0-)f(x)<=-lim(x->0-)(x/ημx) => f(0)<=-1

Αν x ανήκει (0,β) τότε ισχύει ημx>0 αφού ισχύει ημx>0 για κάθε x ανήκει (0,π). Άρα τότε προκύπτει:
f(x)ημx>=-x => f(x)>=-(x/ημx) => lim(x->0+)f(x)>=-lim(x->0+)(x/ημx) => f(0)>=-1

Από τις σχέσεις f(0)<=-1 και f(0)>=-1 προκύπτει ότι f(0)=-1


3) Θεωρούμε την συνάρτηση f(x)=(e^x)/(x+1) με πεδίο ορισμού το Α=(-οο,-1)U(-1,+οο)

Η f είναι συνεχής και παραγωγίσιμη στο Α με πρώτη παράγωγο:
f΄(x)=((e^x)΄(x+1)-(e^x)(x+1)΄)/((x+1)^2)=((e^x)(x+1)-(e^x))/((x+1)^2)=(x(e^x))/((x+1)^2)

Παρατηρούμε ότι f΄(0)=0 και η εξίσωση f΄(x)=0 δεν έχει άλλη λύση.

Η συνάρτηση f είναι συνεχής στο [0,+οο), παραγωγίσιμη στο (0,+οο) και για κάθε x στο (0,+οο) ισχύει f΄(x)>0. Άρα η f είναι γνησίως αύξουσα στο [0,+οο).

Επομένως για α>β>0 θα ισχύει f(α)>f(β) καθώς η f είναι γνησίως αύξουσα στο [0,+οο). Έτσι λοιπόν έχουμε:

α>β>0 => f(α)>f(β) => (e^α)/(α+1)>(e^β)/(β+1) => (e^α)/(e^β)>(α+1)/(β+1) => e^(α-β)>(1+α)/(1+β)


4) f(x)>=x+1
Η Cf διέρχεται από το (0,1) => f(0)=1
Επειδή δεν δίνεται το πεδίο ορισμού της f, θεωρούμε ότι υπάρχουν α,β ανήκουν R με α<0<β ώστε η f να είναι ορισμένη στο (α,β) και για κάθε x στο (α,β) να ισχύει f(x)>=x+1. Παρατηρούμε ότι για x=0 η ανισότητα γίνεται f(0)>=1 που ικανοποιείται αφού f(0)=1.

Δεν δίνεται στην εκφώνηση αλλά πρέπει να γνωρίζουμε ότι η f είναι παραγωγίσιμη στο 0. Επειδή λοιπόν η f είναι παραγωγίσιμη στο 0 τότε προκύπτει:

f΄(0)=lim(x->0)(((f(x)-f(0))/(x-0))=lim(x->0)((f(x)-1)/x)

Επειδή η f ορίζεται στα διαστήματα (α,0), (0,β) τότε ισχύει η ισοδυναμία:

lim(x->0)((f(x)-1)/x)=f΄(0) <=> lim(x->0-)((f(x)-1)/x)=lim(x->0+)((f(x)-1)/x)=f΄(0)


Έχουμε

f(x)>=x+1 => f(x)-1>=x για κάθε x στο (α,β)

Για x στο (α,0) είναι x<0, οπότε
(f(x)-1)/x<=1 => lim(x->0-)[(f(x)-1)/x)<=lim(x->0-)1 => f΄(0)<=1

Για x στο (β,0) είναι x>0, οπότε
(f(x)-1)/x>=1 => lim(x->0+)[(f(x)-1)/x)>=lim(x->0+)1 => f΄(0)>=1

Από τις σχέσεις f΄(0)<=1 και f΄(0)>=1 προκύπτει ότι f΄(0)=1

ευχαριστω πολυ..!!!!!

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Civilara]

ευχαριστω πολυ..!!!!!

Δεν κάνει τίποτα

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[φρι]

Να βρεθει το lim(x-->1+)[ ln(lnx) ]

καποιος??

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 12 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.