Βοήθεια/Aπορίες στα Μαθηματικά Προσανατολισμού

antwwwnis · 21-10-12

z1^n φανταστικός, έστω z1^n=ai, a πραγματικός.
Διαδοχικά

z1^n=ai
sqrt(2)^n (1+i)^n=ai
(1+i)^n=ki

Και διακρίνουμε 4 περιπτώσεις, αυτες με τα υπόλοιπα του n με διαιρέτη το 4.

rebel · 21-10-12

Η παράσταση μηδενίζεται όταν $Re(z_1^n)=0$ , όταν δηλαδή ο $z_1^n$ είναι φανταστικός. Για ποια n γίνεται αυτό;
$\begin{matrix}n=1 & & & \sqrt{2}(1+i) \\ n=2 & & & 4i \\ n=3 &&& 4\sqrt{2}(i-1) \\ n=4 &&& -16\end{matrix}$
Όπως βλέπεις η πρώτη φορά που εμφανίζεται φανταστικός αριθμός είναι για $n=2$ . Αν συνεχίσεις αυτή την διαδικασία θα δεις ότι η εμφάνιση φανταστικού επαναλαμβάνεται από εκεί κι έπειτα κάθε τέσσερα βήματα. Η επόμενη εμφάνιση δηλαδή είναι για $n=6$ κ.ο.κ. Έτσι λοιπόν συμπεραίνουμε ότι η παράσταση μηδενίζεται για
$n=4k+2,\,\,k=0,1,\ldots$

JKaradakov · 21-10-12

Αρχική Δημοσίευση από antwwwnis:
z1^n φανταστικός, έστω z1^n=ai, a πραγματικός.
Διαδοχικά

z1^n=ai
sqrt(2)^n (1+i)^n=ai
(1+i)^n=ki

Και διακρίνουμε 4 περιπτώσεις, αυτες με τα υπόλοιπα του n με διαιρέτη το 4.

Αρχική Δημοσίευση από styt_geia:
Η παράσταση μηδενίζεται όταν $Re(z_1^n)=0$ , όταν δηλαδή ο $z_1^n$ είναι φανταστικός. Για ποια n γίνεται αυτό;
$\begin{matrix}n=1 & & & \sqrt{2}(1+i) \\ n=2 & & & 4i \\ n=3 &&& 4\sqrt{2}(i-1) \\ n=4 &&& -16\end{matrix}$
Όπως βλέπεις η πρώτη φορά που εμφανίζεται φανταστικός αριθμός είναι για $n=2$ . Αν συνεχίσεις αυτή την διαδικασία θα δεις ότι η εμφάνιση φανταστικού επαναλαμβάνεται από εκεί κι έπειτα κάθε τέσσερα βήματα. Η επόμενη εμφάνιση δηλαδή είναι για $n=6$ κ.ο.κ. Έτσι λοιπόν συμπεραίνουμε ότι η παράσταση μηδενίζεται για
$n=4k+2,\,\,k=0,1,\ldots$

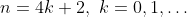
Σας ευχαριστώ και τους 2!

mary-blackrose · 23-10-12

δινεται

Code:

[LATEX]{ z }^{ 2 }+z+1=0[/LATEX]
A)I)να αποδειξετε z^3=1 και να υπολογισετε την τιμη της παραστασης [LATEX]S={ z }^{ 95 }+{ z }^{ 111 }+{ z }^{ 121 }[/LATEX]
II)NΔΟ [LATEX]{ \left( 2z+1 \right)  }^{ 2014 }[/LATEX]ειναι αρνητικος πραγματικος αριθμος.
Β)I)Να βρειτε τους z1,z2 που ικανοποιουν την ισοτητα Im(z1)>0
Γ)ΝΔΟ οι εικονες των Α,Β,Γ των z0=1,z1,z2 σχηματιζουν ισοπλευρο τριγωνο.
Δ)Αν η εικονα Μ ενος μιγαδικου w βρισκεται στον περιγεγραμμενο κυκλο ,να αποδειξετε (ΑΜ)^2+(ΒΜ)^2+(ΓΜ)^2=6

εχω λυσει το Αι)....θα ηθελα αν μπορουσε καποιος να με βοηθησει με τα υπολοιπα ερωτηματα...και να επαληθευσει για το Αι οτι η παρασταση ισουται με 1.

Aris90 · 24-10-12

λοιπον εχω μπει στα μη πεπερασμενα ορια ΧοεR
και εχω καποιες ασκησεις
λεει εστω1 $f(x)=\frac{{2x}^{2}-3x+4}{{x}^{2}-5x+4}$ να βρειτε τα ορια :
$\lim_{x\rightarrow {1}^{-}}$ , $\lim_{x\rightarrow {1}^{+}}$
2)να βρειτε τα α,βΕR ωστε να υπαρχει το οριο της συναρτησης $f(x)\frac{\sqrt{{x}^{2}+3}-2}{x-1}$ ,x>1
$f(x)\frac{{x}^{2}+ax+b-2}{x-1}$ ,x<1 στο σημειο x0=1
αυτες ειναι! θελω να δω πως γινονται μηπως και καταφερω να κανω και κατι αλλα ερωτηματα

vimaproto · 24 Οκτωβρίου 2012

Αρχική Δημοσίευση από Aris90:
λοιπον εχω μπει στα μη πεπερασμενα ορια ΧοεR
και εχω καποιες ασκησεις
λεει εστω1 $f(x)=\frac{{2x}^{2}-3x+4}{{x}^{2}-5x+4}$ να βρειτε τα ορια :
$\lim_{x\rightarrow {1}^{-}}$ , $\lim_{x\rightarrow {1}^{+}}$
2)να βρειτε τα α,βΕR ωστε να υπαρχει το οριο της συναρτησης $f(x)\frac{\sqrt{{x}^{2}+3}-2}{x-1}$ ,x>1
$f(x)\frac{{x}^{2}+ax+b-2}{x-1}$ ,x<1 στο σημειο x0=1
αυτες ειναι! θελω να δω πως γινονται μηπως και καταφερω να κανω και κατι αλλα ερωτηματα

Θα σου περιγράψω τις λύσεις.
1) Για χ=1 ο αριθμητής γίνεται 6 και ο παρονομαστής μηδέν. Αρα το κλάσμα απειρίζεται. Αλλά προς το + άπειρο ή προς το - άπειρο? Εξετάζω το πρόσημο του παρονομαστή λίγο πριν μηδενιστεί. Ο παρονομαστής γράφεται (χ-1)(χ-4). Για χ=1 η χ-4=-3<0 αλλά η χ-1>0 όταν χ-->1 εκ δεξιών.Τότε ο παρονομαστής αρνητικός και το κλάσμα --> στο πλην άπειρο, ενώ χ-1<0 όταν χ-->1 εξ αριστερών, ο παρονομαστής γίνεται θετικός και το κλάσμα --> στο συν άπειρο.
2) Οταν χ>1 δηλ. χ--> στο 1 εκ δεξιών το κλάσμα γίνεται 0/0 γιαυτό πολ/ζω με τη συζυγή παράσταση του αριθμητή και τους δύο όρους και με την αντικατάσταση βρίσκω f=1/2.
Τα ίδια πρέπει να συμβαίνουν και όταν χ<1, δηλ. χ--> 1 εξ αριστερών. Ο αριθμητής πρέπει να διαιρείται ακριβώς από τον παρονομαστή. Κάνοντας τη διαίρεση βρίσκω υπόλοιπο α+β-1 το οποίο πρέπει να είναι =0. Τότε β=1-α και η f(x)=(x-1)(x+1+α)/(χ-1)=χ+1+α και εφ όσο υπάρχει το όριο αυτό για χ=1 πρέπει να ισούται με 1/2 Αρα 1+1+α=1/2 ==> α=-3/2 και β=1+3/2=5/2

Vicky13 · 24-10-12

1)Έστω μιγαδικός z με z<>2 για το οποίο ισχύει Im(z)/ |z-2|^2 + |1-iρίζα3|=0
α)Να δείξετε ότι |4z-8+i|=1
β)Να βρεθεί το σύνολο τιμών του |4z-5+3i|

2)Ισχύει |6z+1|=|4z-1|
α) Να βρεθεί η τιμή |2z+1|
β)Να βρεθεί το σύνολο τιμών του |2z-i|

Βοηθήστε με :/

Aris90 · 24-10-12

Αρχική Δημοσίευση από vimaproto:
Θα σου περιγράψω τις λύσεις.
1) Για χ=1 ο αριθμητής γίνεται 6 και ο παρονομαστής μηδέν. Αρα το κλάσμα απειρίζεται. Αλλά προς το + άπειρο ή προς το - άπειρο? Εξετάζω το πρόσημο του παρονομαστή λίγο πριν μηδενιστεί. Ο παρονομαστής γράφεται (χ-1)(χ-4). Για χ=1 η χ-4=-3<0 αλλά η χ-1>0 όταν χ-->1 εκ δεξιών.Τότε ο παρονομαστής αρνητικός και το κλάσμα --> στο πλην άπειρο, ενώ χ-1<0 όταν χ-->1 εξ αριστερών, ο παρονομαστής γίνεται θετικός και το κλάσμα --> στο συν άπειρο.
2) Οταν χ>1 δηλ. χ--> στο 1 εκ δεξιών το κλάσμα γίνεται 0/0 γιαυτό πολ/ζω με τη συζυγή παράσταση του αριθμητή και τους δύο όρους και με την αντικατάσταση βρίσκω f=1/2.
Τα ίδια πρέπει να συμβαίνουν και όταν χ<1, δηλ. χ--> 1 εξ αριστερών. Ο αριθμητής πρέπει να διαιρείται ακριβώς από τον παρονομαστή. Κάνοντας τη διαίρεση βρίσκω υπόλοιπο α+β-1 το οποίο πρέπει να είναι =0. Τότε β=1-α και η f(x)=(x-1)(x+1+α)/(χ-1)=χ+1+α και εφ όσο υπάρχει το όριο αυτό για χ=1 πρέπει να ισούται με 1/2 Αρα 1+1+α=1/2 ==> α=-3/2 και β=1+3/2=5/2

ευχαριστω νομιζω πως καταλαβα ,ελπιζω να λυσω και τις υπολοιπες που εχω

Vicky13 · 24-10-12

1)Έστω μιγαδικός z με z<>2 για το οποίο ισχύει Im(z)/ |z-2|^2 + |1-iρίζα3|=0
α)Να δείξετε ότι |4z-8+i|=1
β)Να βρεθεί το σύνολο τιμών του |4z-5+3i|

2)Ισχύει |6z+1|=|4z-1|
α) Να βρεθεί η τιμή |2z+1|
β)Να βρεθεί το σύνολο τιμών του |2z-i|

Βοηθήστε με :/

vimaproto · 25 Οκτωβρίου 2012

Αρχική Δημοσίευση από Vicky13:
1)Έστω μιγαδικός z με z<>2 για το οποίο ισχύει Im(z)/ |z-2|^2 + |1-iρίζα3|=0
α)Να δείξετε ότι |4z-8+i|=1
β)Να βρεθεί το σύνολο τιμών του |4z-5+3i|

2)Ισχύει |6z+1|=|4z-1|
α) Να βρεθεί η τιμή |2z+1|
β)Να βρεθεί το σύνολο τιμών του |2z-i|

Βοηθήστε με :/

1)
Από τη σχέση που δίνει για z=x+iy προκύπτει y/[(x-2)^2+y^2] +2=0 (1) ==> (x-2)^2+y^2+y/2=0 Τότε |4z-8+i|=|4(x-2)+(4y+1)i|και λόγω της (1) έχω $\sqrt{{4}^{2}(x-2)^{2}+{y}^{2}+(4y+1)}^{2}=\sqrt{16(-{y}^{2}-\frac{y}{2})+16{y}^{2}+8y+1}=1$
β)Τη λύση δίνει πιο κάτω ο Κώστας

2) Και εδώ από τα δεδομένα καταλήγω στη σχέση χ²+χ+y²=0 την οποία χρησιμοποιώ στις άλλες σχέσεις και τις βρίσκω την α)=1
β) (x+½)²+y²=(½)² και $\sqrt{2}-1\leq |2Z-i|\leq \sqrt{2}+1$

rebel · 25 Οκτωβρίου 2012

Αρχική Δημοσίευση από vimaproto:
$\sqrt{16y-8x+33}\geq 0$

Τα χ,y όμως έχουν μία σχέση εξάρτησης μεταξύ τους η οποία καθορίζεται από την σχέση που δίνεται στην αρχή. Πιστεύω ότι αν δεν καταλήξουμε σε κάτι που να έχει μόνο y ή μόνο χ δεν μπορούμε να εξάγουμε συμπέρασμα για το σύνολο τιμών. Η άποψή μου για το ii) υποερώτημα είναι η εξής:
Από την δοθείσα σχέση
$\frac{Im(z)}{|z-2|^2}+|1-\sqrt{3}i|=0$
με αντικατάσταση $z=x+yi$ συμπληρώσεις τετραγώνων κλπ καταλήγουμε ισοδύναμα στην σχέση
$\Bigl(x-2\Bigr)^2+\Bigl(y+\frac{1}{4}\Bigr)^2=\frac{1}{16}$
Άρα ο γεωμετρικός τόπος των μιγαδικών αυτών είναι κύκλος με $K(2,-1/4),\,\,\rho=1/4$ με εξαίρεση το σημείο $(2,0)$ . Έστω τώρα $M$ η εικόνα ενός μιγαδικού $z$ που ανήκει στον παραπάνω γεωμετρικό τόπο και $A\left(\frac{5}{4},-\frac{3}{4}\right)$ . Τότε
$(AK)-\rho \leq (AM) \leq (AK)+\rho \Leftrightarrow \frac{\sqrt{13}}{4}-\frac{1}{4} \leq (AM) \leq \frac{\sqrt{13}}{4}+\frac{1}{4} \Leftrightarrow \sqrt{13}-1 \leq 4(AM) \leq \sqrt{13}+1\Leftrightarrow \sqrt{13}-1 \leq 4\left|z-\frac{5}{4}+\frac{3}{4}i \right|\leq \sqrt{13}+1\Leftrightarrow \sqrt{13}-1 \leq \left|4z-5+3i \right|\leq \sqrt{13}+1$

...δεν ασχολήθηκα με την δεύτερη άσκηση αλλά φαίνεται παρόμοια.

t00nS · 25-10-12

2 ασκησούλες..
1)να βρείτε το σύνολο τιμών των f(x)=-7x^3+5x+11x+5,χε[0,3]
2)f(x)=5x-3/x-1,χε[1,2]

Βλα · 25-10-12

Αρχική Δημοσίευση από t00nS:
2 ασκησούλες..
1)να βρείτε το σύνολο τιμών των f(x)=-7x^3+5x+11x+5,χε[0,3]
2)f(x)=5x-3/x-1,χε[1,2]

Μήπως έχεις γράψει λάθος την εκφώνηση στην 1)?
Γιατί γράαφεις "11χ+5χ".
Μήπως υπάρχει κάποιο τετράγωνο ή κάτι τέτοιο?
Γιατί αλλιώς θα έγραφες απλά 16χ

Aris90 · 26 Οκτωβρίου 2012

αλλες δυο ασκησεις:
1) δινεται η συναρτηση f(x) $\frac{\left(a+1 \right){x}^{2}+\left(b-2 \right)x+5}{{x}^{2}-4}$
να βρειτε τις τιμες των a.bER για τις οποιες ειναι $\lim_{x\rightarrow 2}f(x)=3$

2) να βρεθει το οριο : $\lim_{x\rightarrow 0}\frac{\sqrt{x+9}-a}{x}$ ,aER

αυτες ηταν οι ασκησεις ειχα και κατι αλλες, αλλα τις ελυσα τωρα με αυτες χρειαζεται να παρουμε περιπτωσεις νομιζω :hmm:

αν δεν κανω λαθος
οποιος προσπαθησει να λυσει τις ασκσεις θα ηθελα να μου τις εξηγησει λιγο αναλυτικα και αν μπορει να τις γραψει σε latex για να τις καταλαβω πιο ευκολα (για μενα πιο ευκολο ειναι να γραφεις σε latex) ευχαριστω εκ'των προτερων

τιποτα ε?

JKaradakov · 26-10-12

$z_1=3+i$
$z_2=2-2i$
$\nu .\alpha .o$ $z_1^2^0 + (z_1-z_2)^2^0=2Re(z_1^2^0)$

rebel · 26-10-12

1) Είναι παρόμοια με προηγούμενες ασκήσεις. Η διαισθητική προσέγγιση είναι ότι αφού ο παρονομαστής πάει στο 0 και το όριο του κλάσματος είναι πραγματικός, τότε και το όριο του αριθμητή πρέπει να είναι 0. Γιατί αν το όριο του αριθμητή ήταν διάφορο του 0 τότε το όριο του κλάσματος θα ήταν $+\infty$ ή $-\infty$ για $x \to 2^+$ ή $x \to 2^-$ αναλόγως και με το πρόσημο του ορίου του αριθμητή. Δες το κεφάλαιο της θεωρίας "Μη πεπερασμένο όριο στο $x_0 \in \mathbb{R}$ ". Η επίσημη λύση συνήθως έχει ως εξής.
Για χ κοντά στο 2 είναι
$f(x)=\frac{(a+1)x^2+(b-2)x+5}{x^2-4} \Rightarrow \\ f(x)(x^2-4)=(a+1)x^2+(b-2)x+5 \Rightarrow \lim_{x \to 2} \left[f(x)(x^2-4)\right]=\lim_{x \to 2}\left[(a+1)x^2+(b-2)x+5\right] \Rightarrow 3\cdot 0=4a+2b+5 \Rightarrow b-2=-\frac{5}{2}-2(a+1) \,\,(1)$
οπότε
$\lim_{x \to 2}f(x)=3 \Rightarrow \lim_{x \to 2}\frac{(a+1)x^2+(b-2)x+5}{x^2-4}=3 \stackrel{(1)}{\Rightarrow} \lim_{x \to 2}\frac{(a+1)x^2-\frac{5}{2}x-2(a+1)x+5}{x^2-4}=3 \Rightarrow \lim_{x \to 2}\frac{x\left[(a+1)x-\frac{5}{2}\right]-2\left[(a+1)x-\frac{5}{2}\right]}{x^2-4}=3 \Rightarrow \lim_{x \to 2}\frac{(x-2)\left[(a+1)x-\frac{5}{2}\right]}{x^2-4}=3 \Rightarrow \lim_{x \to 2}\frac{(a+1)x-\frac{5}{2}}{x+2}=3 \Rightarrow \frac{2a-\frac{1}{2}}{4}=3 \Rightarrow a=6,25$
Αντικαθιστούμε στην (1) και βρίσκουμε $b=-15$

rebel · 26-10-12

Αρχική Δημοσίευση από JKaradakov:
$z_1=3+i$
$z_2=2-2i$
$\nu .\alpha .o$ $z_1^2^0 + (z_1-z_2)^2^0=2Re(z_1^2^0)$

Παρατήρησε ότι $z_1-z_2=1+3i=-i^2+3i=i(3-i)=i\bar{z}_1$

JKaradakov · 26-10-12

Αρχική Δημοσίευση από styt_geia:
Παρατήρησε ότι $z_1-z_2=1+3i=-i^2+3i=i(3-i)=i\bar{z}_1$

Ευχαριστώ!

mary-blackrose · 27 Οκτωβρίου 2012

Code:

1)εστω η παραγωγισιμη συναρτηση [LATEX]f:(0,\infty )\rightarrow R[/LATEX]για την οποια ισχυει:[LATEX]f^{ 3 }\left( x \right) +{ x }^{ 3 }=xf\left    ( x \right) x>0[/LATEX]
Αν η ευθεια ε:ψ+χ-1=0 εφαπτεται στην Cf  στο Χο,να βρειτε το Χο.

2)Αν η F ειναι συνεχης στο R και [LATEX]\lim _{ χ\rightarrow 1 }{ \frac { f\left( x \right) -\sqrt {x+3 }  }{x-1 } =3 } [/LATEX]
i)Ν.Δ.Ο η f ειναι παραγωγισιμη στο Χο=1
ii)να βρεθει η εφαπτομενη της Cf στο Χο=1

3)εστω η συναρτηση f(x)=x+lnx
i)Ν.Δ.Ο υπαρχει η συναρτηση [LATEX]f^{ -1 }[/LATEX]
ii)Να βρεθει η εφαπτομενη της γραφικης παραστασης της [LATEX]f^{ -1 }[/LATEX]στο Χο=-2

Θα ηθελα αν μπορουσε καποιος να μου τις λυσει (αναλυτικα αν ειναι δυνατο)γιατι τις εχω φτασει μεχρι ενα σημειο και μετα απο εκει δεν μπορω να συνεχισω και βγαινουν λαθος αποτελεσματα :/:

JKaradakov · 27-10-12

Έστω οι μιγαδικοί αριθμοί z,w και Ρ,Σ οι αντίστοιχες εικόνες τους στο μιγαδικό επίπεδο. Αν ισχύει η σχέση:
$zw-iw=z+2-i$
να αποδείξετε ότι:
i) όταν το σημείο Ρ κινείται στη μεσοκάθετο ευθεία του τμήματος με άκρα τα σημεία Α(0,1) και Β(-2,1), τότε:
$|z-i|=|z+2-i|$

Βοήθεια/Aπορίες στα Μαθηματικά Προσανατολισμού

Διάσημο μέλος

Πολύ δραστήριο μέλος

Τιμώμενο Μέλος

Εκκολαπτόμενο μέλος

Εκκολαπτόμενο μέλος

Πολύ δραστήριο μέλος

Δραστήριο μέλος

Εκκολαπτόμενο μέλος

Δραστήριο μέλος

Πολύ δραστήριο μέλος

Πολύ δραστήριο μέλος

Εκκολαπτόμενο μέλος

Πολύ δραστήριο μέλος

Εκκολαπτόμενο μέλος

Τιμώμενο Μέλος

Πολύ δραστήριο μέλος

Πολύ δραστήριο μέλος

Τιμώμενο Μέλος

Εκκολαπτόμενο μέλος

Τιμώμενο Μέλος