Βοήθεια/Aπορίες στα Μαθηματικά Προσανατολισμού

[drosos]

Ναι θ υπαρχουν πολυ τροποι αλλα ειχα φαει μεγαλο κολλημα(τουλαχιστον μιση ωρα) και μπερδεψα ενα προσημο και το χανω ολο... \Σιγα δεν εδινα και πανελληνιες

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Or3st1s SOAD]

Παιδια μπορει καποιος να κοιταξει το θεμα μου στην προηγουμενη σελιδα?
Ευχαριστω

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[rebel]

είναι;

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Or3st1s SOAD]

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[g1wrg0s]

Αυτο εννοει, παντως απο το αρχικο ποστ δεν εβγαινε αυτο

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Or3st1s SOAD]

Ναι οπως το γραφει ο γιωργος.
Το latex πως το περναω στην απαντηση που γραφω? Eγραψα

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[rebel]

Για το δεύτερο ερώτημα έχουμε



άρα είναι η μεσοκάθετος του ευθύγραμμου τμήματος ΑΒ με .

Για το τέταρτο είναι



οπότε δοκίμασα να δείξω ότι



αφού η (fog)(x) είναι γνήσια αύξουσα, και

αλλά δεν τα κατάφερα. Ίσως έχω λάθος, θα το ξανακοιτάξω.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[tazoulini]

Γεια σας παιδια...μπορει κανεις να με βοηθησει στα θεματα 11(σελ.354) και 4(σελ 352) του μπαρλα τευχος Α?(δεν μπορω να γραψω ριζες και τετραγωνα στον υπολογιστη) οποιος εχει το βιβλιο και γνωριζει ας με βοηθησει...Ευχαριστω!

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[gkm]

χρησιμοποιήθηκε ο τύπος για το πεπερασμένο άθροισμα όρων γεωμετρικής προόδου με πρώτο όρο 1 και λόγο -i. Τώρα

• 
• 

Ευχαρίστω πάρα πολυ για τον χρονο σου, όμως ακόμα δεν λέω να το καταλάβω
Γιατί έβγαλες κοινό παράγοντα το i^3; Μετά πήρες αυτόν τον τύπο

και αντικατέστησες. Τώρα που έβγαλες κοινό παράγοντα το i^3 δεν είναι πρώτος όρος το 1; γιατι το ν το αντικατέστησες 2ν-1 αφού ο τελευταίος όρος είναι εις την 2ν-2; Οταν λες "χρησιμοποιήθηκε ο τύπος για το πεπερασμένο άθροισμα

όρων γεωμετρικής προόδο" τι εννοείς; ποιον τύπο; ποιο πεπερασμένο αθροισμα; μετά πέρνεις το ν ίσο με το 2κ και το 2κ+1 πως; και πως καταλήγεις στο αποτέλεσμα αυτό; Αν μπορούσες να εξηγήσεις την λύση σου πιο αναλυτικά, θα ήταν υπέροχο.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[rebel]

γιατί έβγαλες κοινό παράγοντα το i^3;

Θα μπορούσα και να μην το είχα βγάλει. Απλά αυτό που μένει μέσα στην παθένθεση είναι άθροισμα όρων γεωμετρικής προόδου με πρώτο όρο το 1 οπότε μου αρέσει περισσότερο έτσι. Λυπάμαι αν σε μπέρδεψα.

Μετά πήρες αυτόν τον τύπο

και αντικατέστησες. Τώρα που έβγαλες κοινό παράγοντα το i^3 δεν είναι πρώτος όρος το 1;

ναι

γιατι το ν το αντικατέστησες 2ν-1 αφού ο τελευταίος όρος είναι εις την 2ν-2;

Το ν στον τύπο

είναι το πλήθος των όρων του αθροίσματος. Στο συγκεκριμένο άθροισμα για να μετρήσεις πόσους όρους έχουμε βλέπεις τους εκθέτες. Ξεκινάνε από 0, αφού και φθάνουν μέχρι 2ν-2. Συνολο 2ν-1. Αν δεν καταλαβαίνεις γιατί, σκέψου πόσους όρους θα είχε το άθροισμα αν οι εκθέτες ήταν 0,1,...,10. Θα είχε 11 όρους μαζί με το 0. Σωστά;

Οταν λες "χρησιμοποιήθηκε ο τύπος για το πεπερασμένο άθροισμα όρων γεωμετρικής προόδο" τι εννοείς; ποιον τύπο;

Ακριβώς αυτόν που έγραψες

ποιο πεπερασμένο αθροισμα; μετά πέρνεις το ν ίσο με το 2κ και το 2κ+1 πως; και πως καταλήγεις στο αποτέλεσμα αυτό; Αν μπορούσες να εξηγήσεις την λύση σου πιο αναλυτικά, θα ήταν υπέροχο.

Όταν λέω πεπερασμένο εννοώ ότι ξεκινάει από κάπου και τελειώνει κάπου. Αν θεωρήσουμε για παράδειγμα το άθροισμα τότε αυτό δεν είναι πεπερασμένο αλλά άπειρο.
Όσο για τις περιπτώσεις που παίρνω εννοώ ότι αν ο ν είναι άρτιος (ν=2κ) τότε το S είναι -1 ενώ αν ο ν είναι περιττός (ν=2κ+1) τότε το S είναι -i. Μπορείς να βάλεις όπου ν=1,2,3,4,5 κλπ στον τελευταίο τύπο για να το επαληθεύσεις.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Gver]

Παιδια θελω βοηθεια επειδη εχω κολλησει σε κατι αν εχω

Και θελω να δειξω οτι αν Ζ1,Ζ2 ριζες της P(Z)=0
τοτε Ζ1^ν+Ζ2^ν ειναι πραγματικος

Παιδια θελω βοηθεια επειδη εχω κολλησει σε κατι αν εχω

Και θελω να δειξω οτι αν Ζ1,Ζ2 ριζες της P(Z)=0
τοτε Ζ1^ν+Ζ2^ν ειναι πραγματικος

βλακεια το βρηκα τσαμπα ειχα κολλησει ειναι συζυγεις αρα το αθροισμα τους ειναι πραγματικος

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[dannaros]

Γεια σας παιδια...μπορει κανεις να με βοηθησει στα θεματα 11(σελ.354) και 4(σελ 352) του μπαρλα τευχος Α?(δεν μπορω να γραψω ριζες και τετραγωνα στον υπολογιστη) οποιος εχει το βιβλιο και γνωριζει ας με βοηθησει...Ευχαριστω!

ρε απαντήστε και σε αυτό ρε παιδιά... ποιος είναι αυτός ο μπαρλάς?

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[tsarachaf]

ρε απαντήστε και σε αυτό ρε παιδιά... ποιος είναι αυτός ο μπαρλάς?

Βοήθημα μαθηματικών είναι ο μπάρλας, από τα πιο ευρέως χρησιμοποιούμενα...

Θα βοηθούσα, αλλά δεν έχω εδώ τον δικό μου...

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[g1wrg0s]

Γεια σας παιδια...μπορει κανεις να με βοηθησει στα θεματα 11(σελ.354) και 4(σελ 352) του μπαρλα τευχος Α?(δεν μπορω να γραψω ριζες και τετραγωνα στον υπολογιστη) οποιος εχει το βιβλιο και γνωριζει ας με βοηθησει...Ευχαριστω!

Θεμα 4 απο Μπαρλα στη σελιδα 352 (αν εχουμε το ιδιο)

α) Σου ζητα να βρεις το γεωμετρικοο τοπο (τον ονομαζει Cα ) των σημειων Μ του επιπεδου που ειναι εικονες των ζ=χ+yι με χ,y ε IR, που εικανοποιουν τη σχεση με α ε IR

Το μονο που μπορεις να εκμεταλευτεις ειναι την σχεση που σου δινει και σου λεει οτι ισχυει για τους z .Γνωριζω απο θεωρια οτι αρα η ισοτητα γινεται:
=0 =>2x-α+2y=0 με α ε IR

Ογεωμετρικος τοπος στον οποιο κινουνται οι οικονες του z ειναι μια ωραιοτατη ευθεια με εξισωση 2x-α+2y=0 με α ε IR

β) Διαβαζοντας το ερωτημα παιρνουμε τα δεδομενα και το ζητουμενο του. Αρχικα λεει "Αν Α(-1/2, 3/2) ε Cα" αρα καταλαβαινουμε οτι οι συντεταγμενες του Α ικανοποιουν την εξισωση της ευθειας (Cα) .
Για χ=-1/2 και y=3/2 εχω 2*(-1/2)-α+2*3/2=0=>...=>α=2
Οποτε η εξισωση του Cα ειναι 2χ-2+2y=0 => y=-x+1 δηλαδη Ca : y=-x+1, με χ ε ΙR (δεν δινει καποιο περιορισμο για το x)

Μετα λεει "Να προσδιορισετε σημειο Β ε Cα" αυτο ειναι το ζητουμενο, και συμπληρωνει λεγοντας οτι η μεσοκαθετος του ΑΒ θα περνα απο το κεντρο του κυκλου με εξισωση |z+1-3i|=β, με β>0

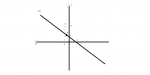
Ξεκιναμε απο την εξισωση του κυκλου και προσδιοριζουμε το κεντρο του |z+1-3i|=β => |z-(-1+3i)|=β , δηλαδη το κεντρο του κυκλου ειναι το Κ(-1,3) (βλ. θεωρια σχολικου βιβλιου για το πως βρηκα το κεντρο του κυκλου)
Αρα το σχημα μεχρι τωρα εχει ως εξης (Πρωτο σχημα)
Η εξισωση της μεσοκαθετου (την ονομαζω ε ) του ΑΒ ειναι y-yo=λε * (χ-χο) (1) (οπου λε ο συντελεστης διευθυνσης της ευθειας ε)
Το ευθυγραμο τμημα ΑΒ ανηκει στην ευθεια Cα (αφου ως δεδομενα δινει Α ε Cα και Β ε Cα ) αρα εχουν τον ιδιο συντελεστη διευθυνσης με αυτη. Δηλαδη λΑΒ= λCα=-1 . ομως οπως γνωριζουμε απο την δευτερα λυκειου, οταν δυο ευθειες ή ευθυγραμμα τμηματα ειναι καθετα μετξυ τους τοτε εχουν αντιθετοαντιστροφους συντελεστες διευθυνσης. Δηλαδη ισχυει λΑΒ * λε= -1=> ...=>λε=1
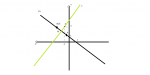
Επισης η ασκηση λεει οτι το κεντρο Κ του κυκλου διερχεται απο τη μεσοκαθετο του ΑΒ, αρα οι συντεταγμενες του επαληθευουν την εξισωση της μεσοκαθετου του ΑΒ. Μετα απο αυτα η σχεση (1) γινεται y-yk=1*(x-xk) =>...=>y=x+4 (η εξισωση της μεσοκαθετου του ΑΒ και στην ουσια η ευθεια ε)

Οπως φαινεται απο το δευτερο σχημα η ευθεια ε περναει απο το μεσο Μ του ΑΒ (λογικο αφου ειναι η μεσοκαθετοςς του). Το σημειο Μ επαληθευει δυο εξισωσεις. Αυτη της ευθειας ε και της ευθειας Cα. Λυνοντα το συστημα των δυο εξισωσεων θα βρουμε τις συντεταγμενες του Μ.

y=x+4
y= -x+1 ...
Αν το λυσεις τοτε βγαινει Μ( -3/2, 5/2)
Ξαναλεω οτι το Μ ειναι το μεσο του Αβ οποτε ισχυει Μ( (x Α+xB )/2 , (yA+yB)/2 ) .Απο εκει περα εχω (x Α+xB )/2 = -3/2 (το εχω βρει απο πανω) =>...=>xΒ= -5/2 και ομοια βγαινει οτι yΒ= 7/2

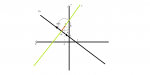
Επομενως οι συντεταγμενες του ζητουμενου Β (βλ. σχημα 3) ειναι Β(-5/2, 7/2) (ο Μπαρλας συμφωνει μαζι μου)
Οσον αφορα το τελευταιο υποερωτημα. Ζητα την ακτινα του κυκλου (το β ) με κεντρο το Κ ετσι, ωστε ο κυκλος να εφαπτεται στην ευθεια Cα. Αν δεις απο το σχημα με τον αθλιο κυκλο θα παρατηρησεις οτι στην ουσια ζητα το ευθυγραμο τμημα ΜΚ αφου μονο τοτε (αν δηλαδη β=ΜΚ ) ο κυκλος εφαπτεται στη Cα.
ΜΚ= =...= /2

Ελπιζω να βοηθησα και να ειναι το σωστο θεμα !

Αυτα ειναι τα σχηματα

Γεια σας παιδια...μπορει κανεις να με βοηθησει στα θεματα 11(σελ.354) και 4(σελ 352) του μπαρλα τευχος Α?(δεν μπορω να γραψω ριζες και τετραγωνα στον υπολογιστη) οποιος εχει το βιβλιο και γνωριζει ας με βοηθησει...Ευχαριστω!

Θεμα 11 Μπαρλας σελιδα 354

α) Λυνεις την εξισωση κανονικα με διακρινουσα κτλ .Βγαινει Δ= -4(ημθ)^2 <0 για καθε θ ε (0,2π) (Αυτος λεει να λυθει για καθε θ ε [0,2π) αλλα δεν ξερω τι να κανω αν θ=0 αφου βγαινει Δ=0) και Z1= συνθ+iημθ , Z2=συνθ-iημθ

β) Απο εδω και περα δεν ειμαι σιγουρος και θα γραψω πως θα το ελυνα εγω...
Για να βρισκονται οι εικονες των Ζ1,Ζ2 στον μοναδιαιο κυκλο θα πρεπει οι συντεταγμενες τους να βρισκονται μεταξυ του -1 και του 1 (αν σχηματισεις ενα μοναδιαιο κυκλο τοτε θα δεις γιατι αυτα τα νουμερα)
Εστω Β,Γ οι εικονες των Ζ1,Ζ2 αντιστοιχα, με Β(Χ1,y2) και Γ(Χ2,y2). Για να ανηκουν το Β στο μοναδιαιο κυκλο πρεπει να ισχυει:
-1<=Χ1<=1 και -1<=y1<=1 => (ομως Χ1=συνθ και y1=ημθ)
=> -1<=συνθ<=1 και -1<=ημθ<=1 που ισχυουν για καθε θ ε [0,2π)
Αρα το Β , δηλαδη η εικονα του Ζ1 ανηκει στον μοναδιαιο κυκλο.

Ομοιως αποδεικνυεις οτι το Γ δηλαδη η εικονα του Ζ2 ανηκει στον μοναδιαιο κυκλο.

γ) οι εικονες των Ζ1,Ζ2 κινουνται στον μοναδιαιο κυκλο οπως αποδειξαμε παραπανω για καθε τιμη του θ ε [0,2π) . Δηλαδη αναλογα με το ποια τιμη εχει το θ ο Ζ1 και ο Ζ2 εινα διαφορετικοι. Το ζητουμενο του ερωτηματος ειναι να βρεις την τιμη του θ για την οποια το |Ζ1-Ζ2| παιρνει τη μεγιστη τιμη.
! θυμιζω οτι το μετρο της διαφορας δυο μιγαδικων ειναι ισο με την αποσταση των εικονων τους (βλ. σελιδα 98 σχολικου βιβλιου)
Ισχυει δηλαδη |Ζ1-Ζ2|= (ΒΓ)
Αρα επι της ουσιας ζητα να βρουμε για ποια τιμη του θ το ΒΓ ειναι μεγιστο.
!θυμιζω οτι σε ενα κυκλο η μεγιστη αποσταση που μπορουν να εχουν δυο σημεια ειναι 2ρ=δ (οπου ρ η ακτινα και δ η διαμετρο του κυκλου)
Και αφου ο κυκλος ειναι μοναδιαιος τοτε ρ=1 ,αρα δ=(ΒΓ)max=2

Επομενως πρεπει να λυσω την εξισωση |Ζ1-Ζ2|= (ΒΓ)max =>|Ζ1-Ζ2|=2 => |συνθ+iημθ-συνθ+iημθ|=2 => |iημθ|=1 =>|ημθ|=1 που ισχυει θ=π/2 ή θ=3π/2 (σε rad)

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[tazoulini]

σε ευχαριστω παρα πολυ το 4ο το καταφερα μονη μου τελικα....στο 11 δεν μπορουσα καν να αρχισω απο καπου....και παλι σε ευχαριστω!!!!!!!!!!

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[rebel]

Για να ανηκουν το Β στο μοναδιαιο κυκλο πρεπει να ισχυει:
-1<=Χ1<=1 και -1<=y1<=1 => (ομως Χ1=συνθ και y1=ημθ)
=> -1<=συνθ<=1 και -1<=ημθ<=1 που ισχυουν για καθε θ ε [0,2π)

Δεν ισχύει αυτό γιατί π.χ. αν τότε .Η εικόνα ενός μιγαδικού z ανήκει στον μοναδιαίο κύκλο αν και μόνο αν . Εδώ έχουμε



οπότε πράγματι ανήκουν.

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Βασίλης Δ.]

Kαλησπέρα...Μπορεί κάποιος να με βοηθήσει με αυτές τις 2 συναρτήσεις?

Και στις δύο f : R ---> R
g(f(x))=2x^5 + e^f(x) +1 , x e R
f(f(x))=f(x) +e^x -1 , x e R

Kαι στις δύο πρεπει να δειξεις πως ειναι 1-1

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[g1wrg0s]

Ζητα να δειξεις οτι οι g(f(x)) και f(f(x)) ειναι ενα προς ενα ; Σου λεει οτι η f ειναι 1-1 ;

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[Βασίλης Δ.]

οχι οχι ειναι διαφορετικες ασκησεις..απλα και οι δυο ζητανε να δειξεις οτι ειναι 1-1

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.

[antwwwnis]

οχι οχι ειναι διαφορετικες ασκησεις..απλα και οι δυο ζητανε να δειξεις οτι ειναι 1-1

Δηλαδή στην πρώτη πρέπει να αποδείξεις ότι οι f,g είναι και οι δυο 1-1;

 

Σημείωση: Το μήνυμα αυτό γράφτηκε 13 χρόνια πριν. Ο συντάκτης του πιθανόν να έχει αλλάξει απόψεις έκτοτε.